Trignometry
5.0(1)
Learn
Practice Test
Spaced Repetition
Match
FlashcardsCard Sorting
1/84
Earn XP
Description and Tags
Actually helps with memorizing
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
85 Terms
1
New cards
sin 0
0
2
New cards
cos 0
1
3
New cards
sin π/6
1/2
4
New cards
cos π/6
√(3)/2
5
New cards
sin π/4
√2/2
6
New cards
cos π/4
√2/2
7
New cards
sin π/3
√3/2
8
New cards
cos π/3
1/2
9
New cards
sin π/2
1
10
New cards
cos π/2
0
11
New cards
sin 2π/3
√3/2
12
New cards
cos 2π/3
-1/2
13
New cards
sin 3π/4
√2/2
14
New cards
cos 3π/4
-√2/2
15
New cards
sin 5π/6
1/2
16
New cards
cos 5π/6
-√3/2
17
New cards
sin π
0
18
New cards
cos π
-1
19
New cards
sin 7π/6
-1/2
20
New cards
cos 7π/6
-√3/2
21
New cards
sin 5π/4
-√2/2
22
New cards
cos 5π/4
-√2/2
23
New cards
sin 4π/3
-√3/2
24
New cards
cos 4π/3
-1/2
25
New cards
sin 3π/2
-1
26
New cards
cos 3π/2
0
27
New cards
sin 5π/3
-√3/2
28
New cards
cos 5π/3
1/2
29
New cards
sin 7π/4
-√2/2
30
New cards
cos 7π/4
√2/2
31
New cards
sin 11π/6
-1/2
32
New cards
cos 11π/6
√3/2
33
New cards
sin 2π
0
34
New cards
cos 2π
1
35
New cards
tan π/6
√3/3
36
New cards
tan π/4
1
37
New cards
tan π/3
√3
38
New cards
tan 2π/3
-√3
39
New cards
tan 3π/4
-1
40
New cards
tan 5π/6
-√3/3
41
New cards
tan π
0
42
New cards
tan 7π/6
√3/3
43
New cards
tan 5π/4
1
44
New cards
tan 4π/3
√3
45
New cards
tan 3π/2
undefined
46
New cards
tan π/2
undefined
47
New cards
tan 5π/3
-√3
48
New cards
tan 7π/4
-1
49
New cards
tan 11π/6
-√3/3
50
New cards
tan 0
0
51
New cards
tan 2π
0
52
New cards
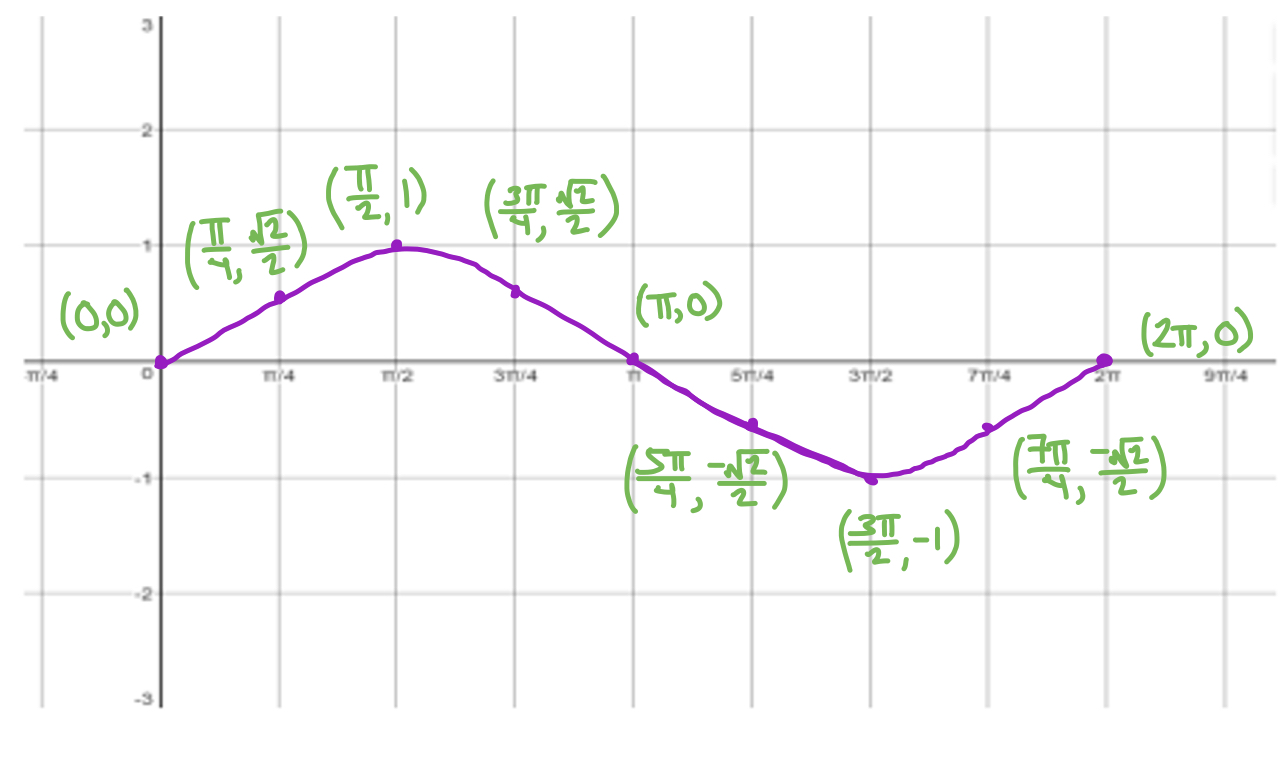
What graph is this?
f(x) = sin x
53
New cards
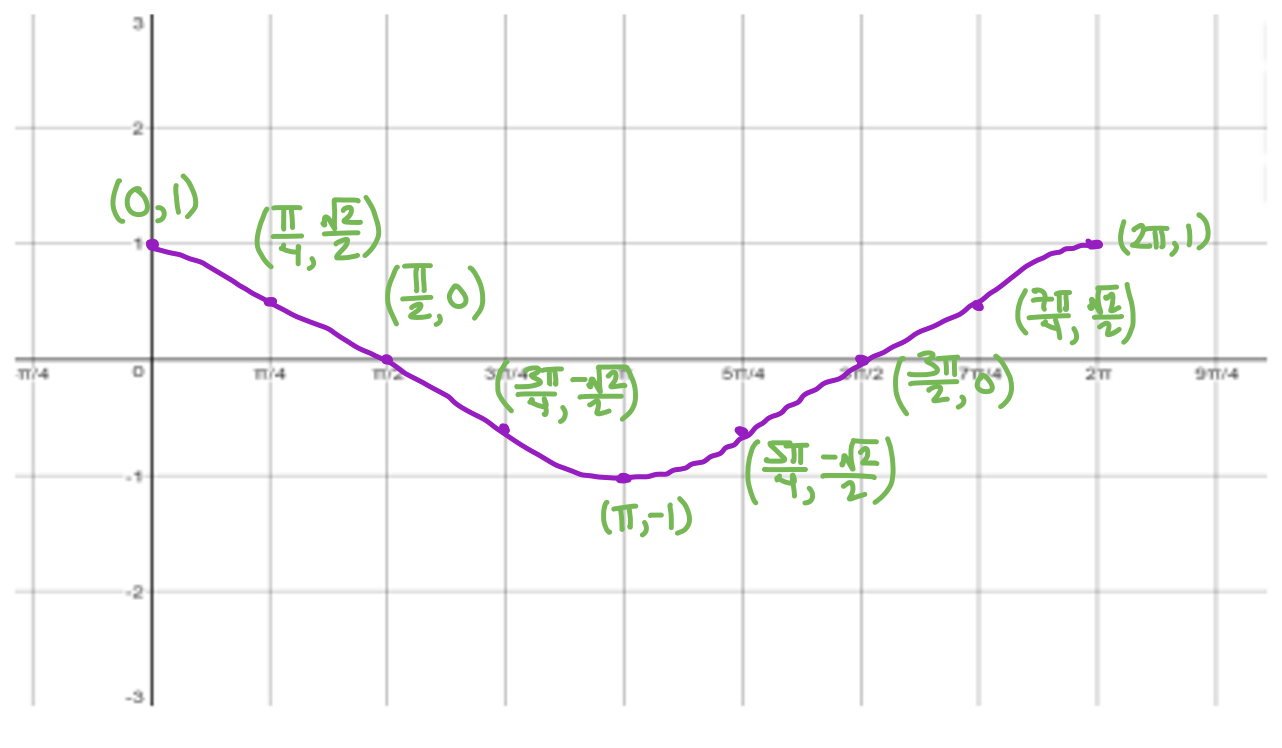
What graph is this?
f(x) = cos x
54
New cards
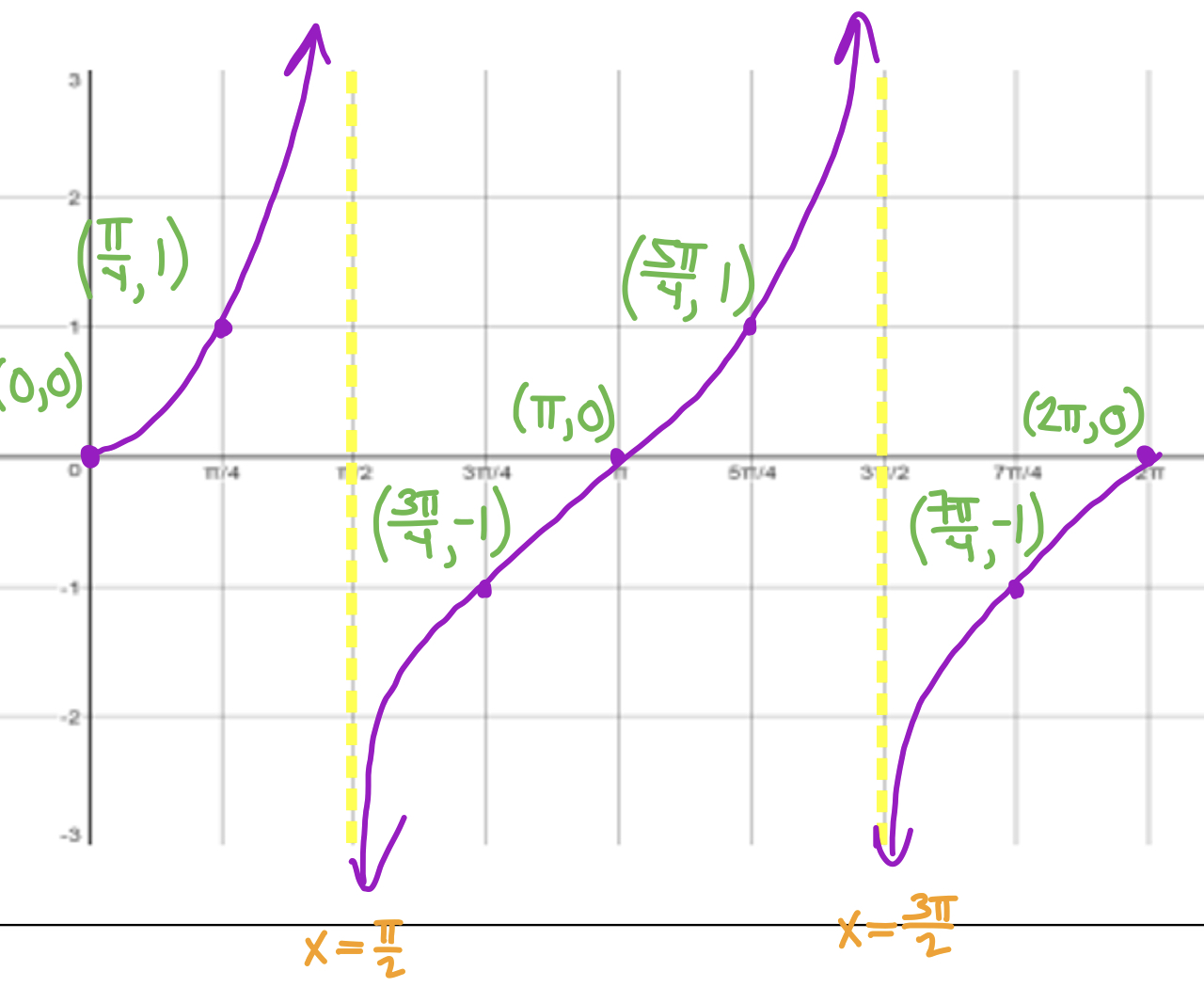
What graph is this?
f(x) = tan x
55
New cards
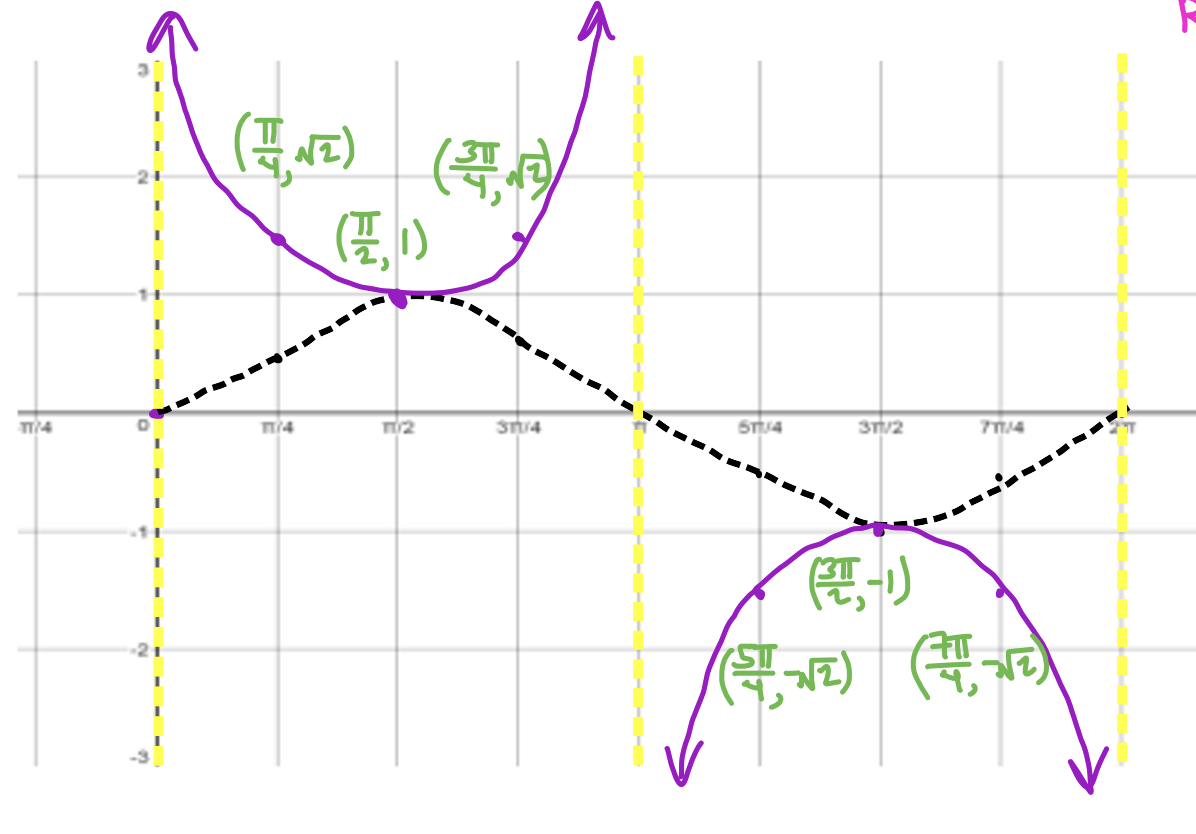
What graph is this?
f(x) = csc x
56
New cards
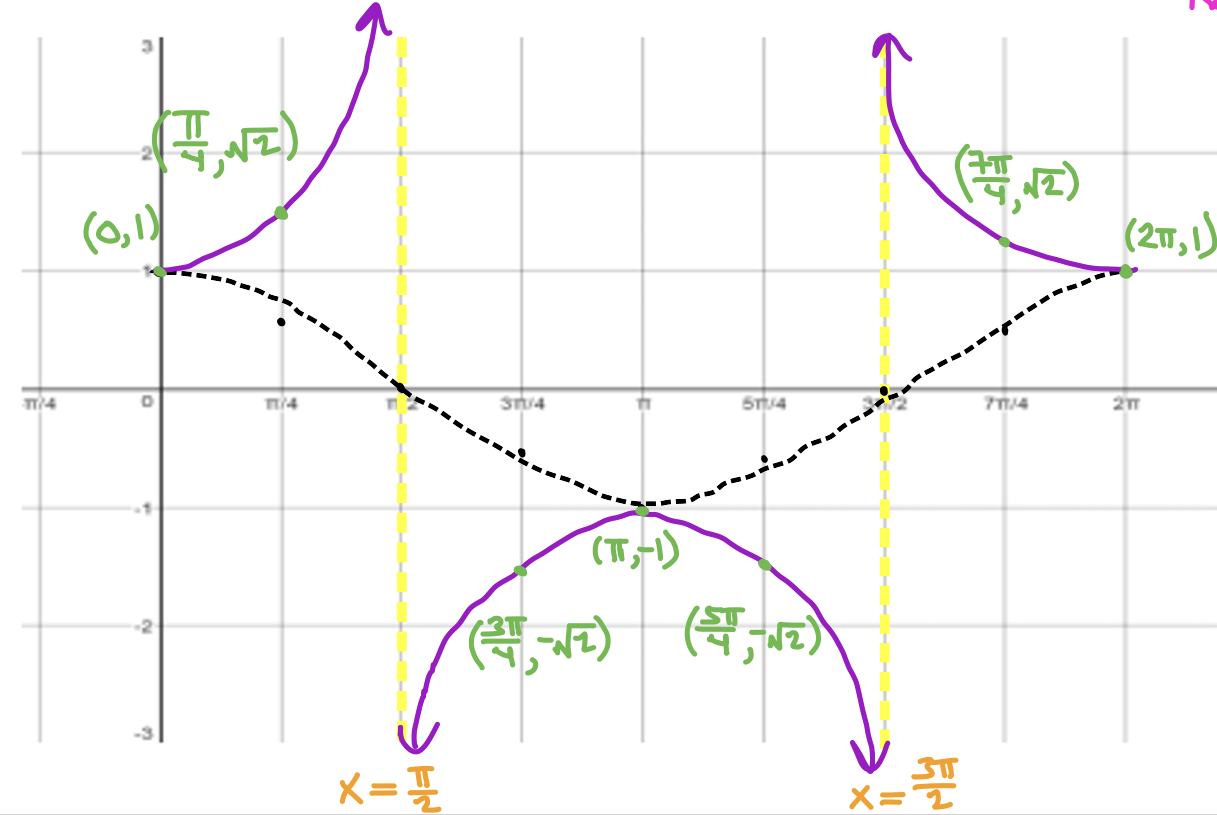
What graph is this?
f(x) = sec x
57
New cards
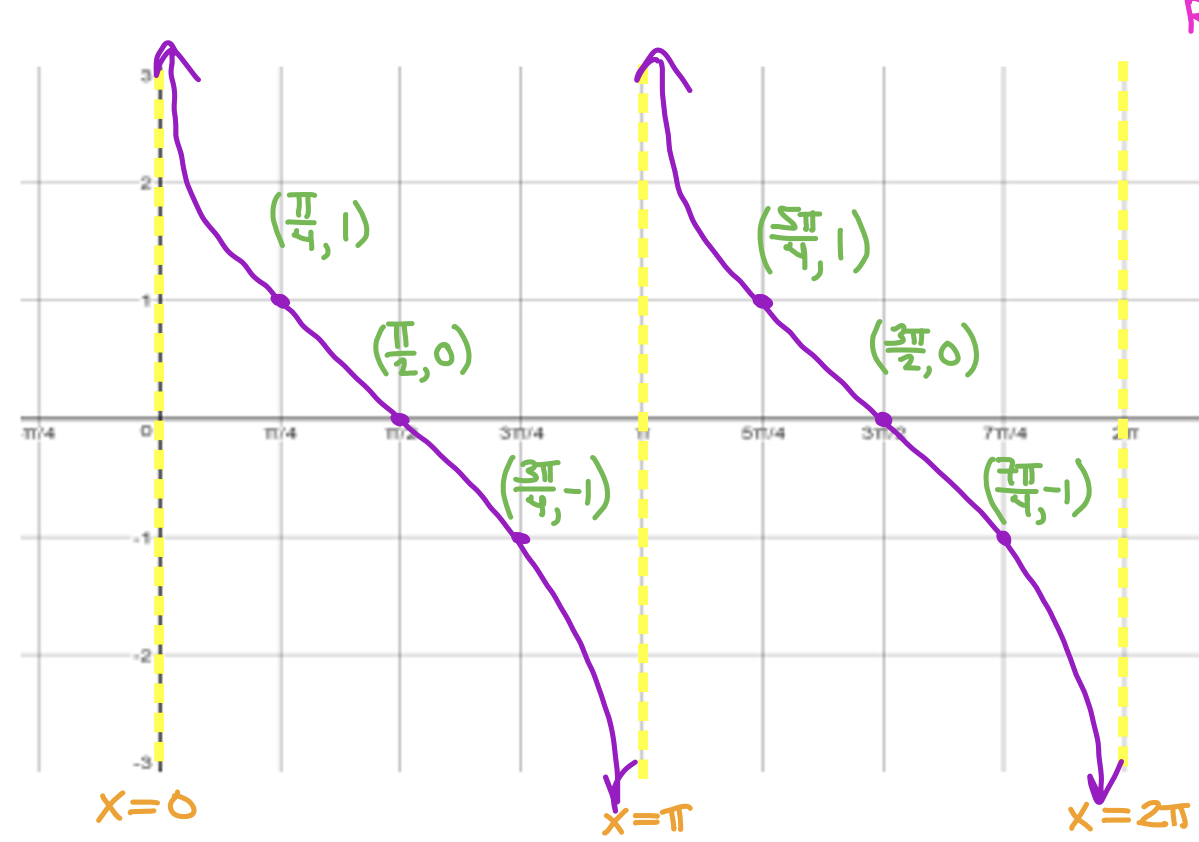
What graph is this
f(x) = cot x
58
New cards
Domain for sin x
(-∞, ∞)
59
New cards
Range for sin x
\[-1,1\]
60
New cards
Domain for cos x
(-∞,∞)
61
New cards
Range for cos x
\[-1,1\]
62
New cards
Domain for tan x
x ≠ π/2 + πk, KEZ
63
New cards
Range for tan x
(-∞,∞)
64
New cards
Domain for csc x
x ≠ πk, KEZ
65
New cards
Range for csc x
(-∞, -1\] U \[1, ∞)
66
New cards
Domain for sec x
x ≠ π/2 + πk, KEZ
67
New cards
Range for sec x
(-∞, -1\] U \[1, ∞)
68
New cards
Domain for cot x
x ≠ πk, KEZ
69
New cards
Range for cot x
(-∞,∞)
70
New cards
Asymptote for csc x
x = πk, KEZ
71
New cards
Asymptote for sec x
x = π/2 + πk, KEZ
72
New cards
Asymptote for cot x
x = πk, KEZ
73
New cards
Asymptote for tan x
x = π/2 + πk, KEZ
74
New cards
Zeros for sin x
x = πk, KEZ
75
New cards
Zeros from cos x
x = π/2 + πk, KEZ
76
New cards
Zeros from tan x
x = πk, KEZ
77
New cards
Zeros from csc x
None
78
New cards
Zeros from sec x
None
79
New cards
Zeros from cot x
x = π/2 + πk, KEZ
80
New cards
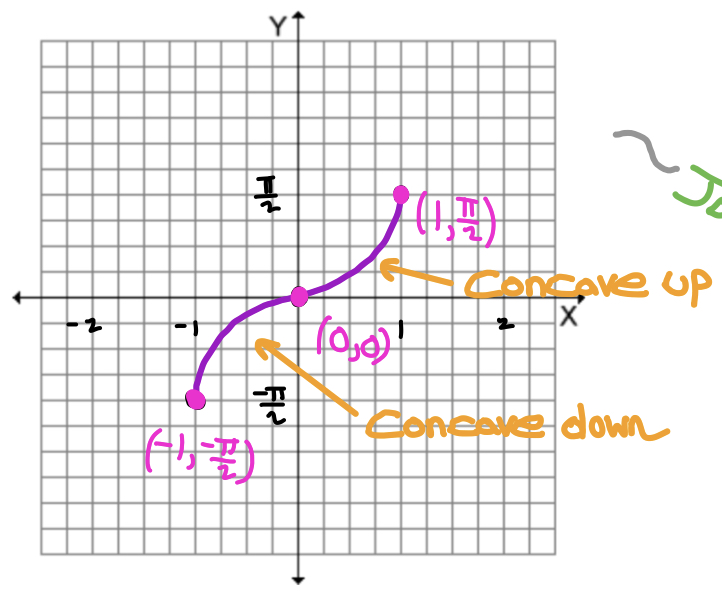
What is this graph?
g(x) = arcsin x
81
New cards
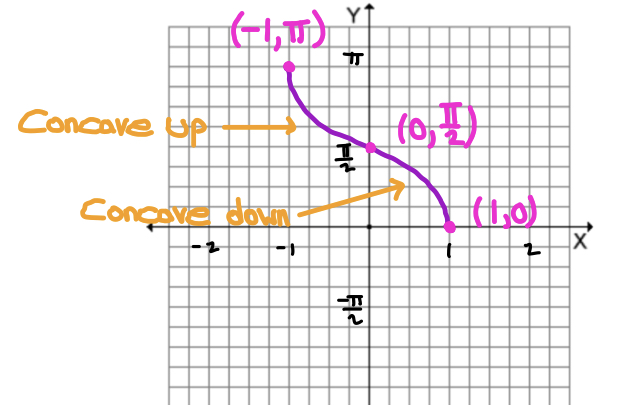
What is this graph?
g(x) = arccos x
82
New cards
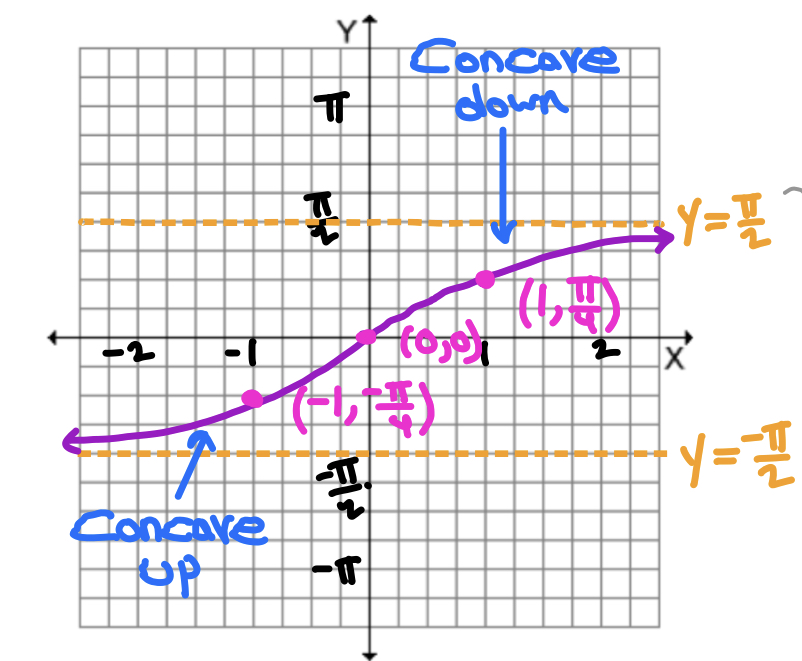
What is this graph?
g(x) = arctan x
83
New cards
What is the range of g(x) = arcsin x
\[-π/2, π/2\]
84
New cards
What is the range of g(x) = arccos x
\[0, π\]
85
New cards
What is the range of g(x) = arctan x
(-π/2, π/2)
Note 
Flashcards (243)