Measures of Variability

variability

a measure of how “close together” or “far apart” scores are in a dataset

range

the difference between the largest and smallest values in a dataset

• = max-min

• very sensitive to outliers

variance

a measure of spread relative to the scatter score of values about their mean

• a numerical measure of how far, on average, a score in the dataset falls from the mean of all scores

• narrow vs wide distribution using mean as a reference pt

population variance

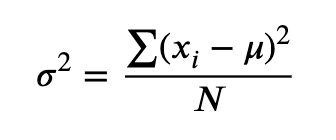
sample variance

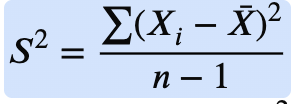
Steps for calculating the sample variance

1. Calculate the mean of the dataset (X̄)

2. Calculate the deviation of every score value from the mean Xi−X̄

3. Square all of the deviations (Xi−X̄)²

4. Add all of the squared deviations ∑(Xi−X̄)²

5. Divide by “n-1” (Xi−X̄)² / n-1

standard deviation

the square root of the variance

percentiles

given a set of n observations (X₁ , X₂ ….X_n ), the p^th percentile, P, is the value of X such that p% or less of the observations are less than P and (100-p)% or less of the observations are greater than P

25th percentile (first quartile)

its location is the n+1/4 ordered observation in the dataset

50th Percentile (second quartile)

its location is the 2(n+1)/4 ordered observation in the dataset

• this is equal to the median in a dataset

75th Percentile (third quartile)

its location is the 3(n+1)/4 ordered observation in a dataset

boxplots

A 5-# summary of data consisting of the Min, Max, and all 3 Quartiles

interquartile range (IQR)

the difference between the third and first quartiles

advantage of the IQR

it is superior ti the traditional range because it only looks at the variability of the middle 50% of the observations and is therefore less sensitive to extreme scores/outliers

outlier

an observation whose value, X, either exceeds the value of the 3^rd Quartile by a magnitude greater than 1.5(IQR) or is less than the value of the 1^st Quartile by a magnitude greater than 1.5(IQR)

• Is there a value, X, that is either <Q₁ - 1.5(IQR) or >Q₃ + 1.5(IQR)