Geo U4 & U5 - Triangle Congruence and Inequality

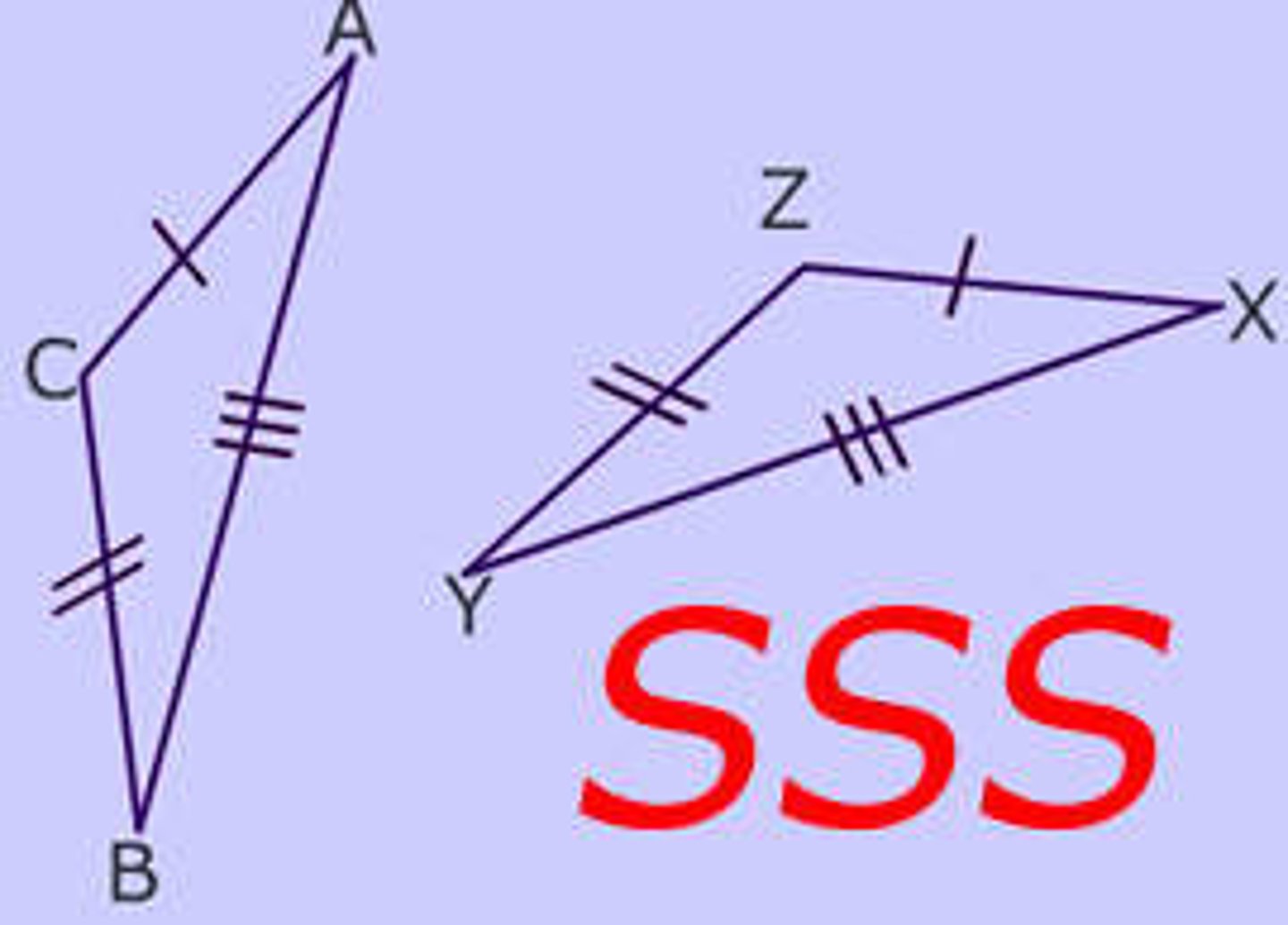
U4/5: Side-Side-Side (SSS) Postulate

If 3 pairs of correspondjng sides are congruent, theb the triabgles are congruent.

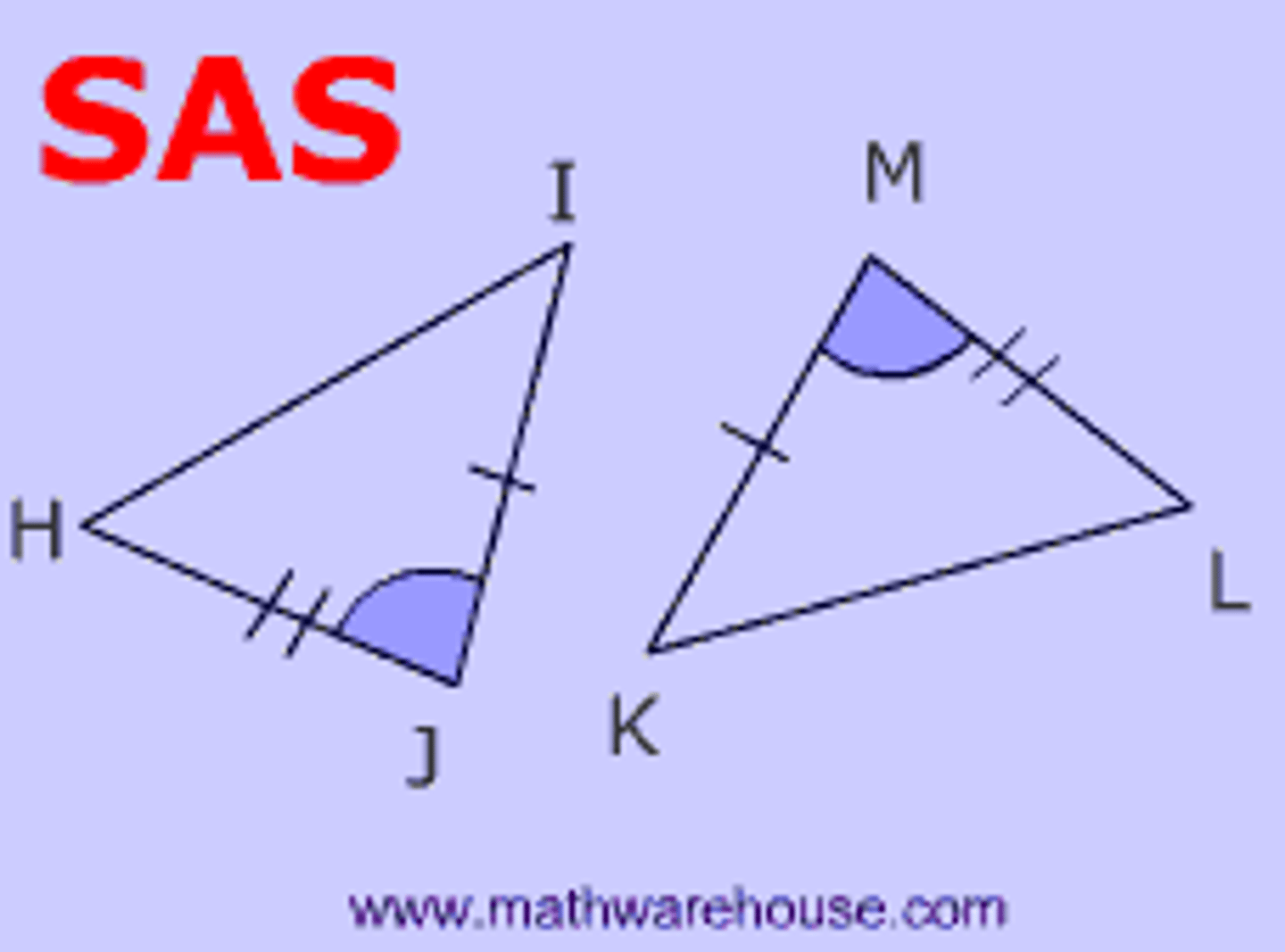
U4/5: Side-Angle-Side (SAS) Postulate

If 2 sides and the included angle of one triangle are congruent to those parts of another triangle, then the 2 triangles are congruent.

-*included angle= angle in between

U4/5: Without knowing all 6 parts of a triangle we can show 2 triangles are congruent using...

AAA, HL, AAS, ASA, SSS

U4/5: Triangle Writing

Corresponding vertices must be in the same order

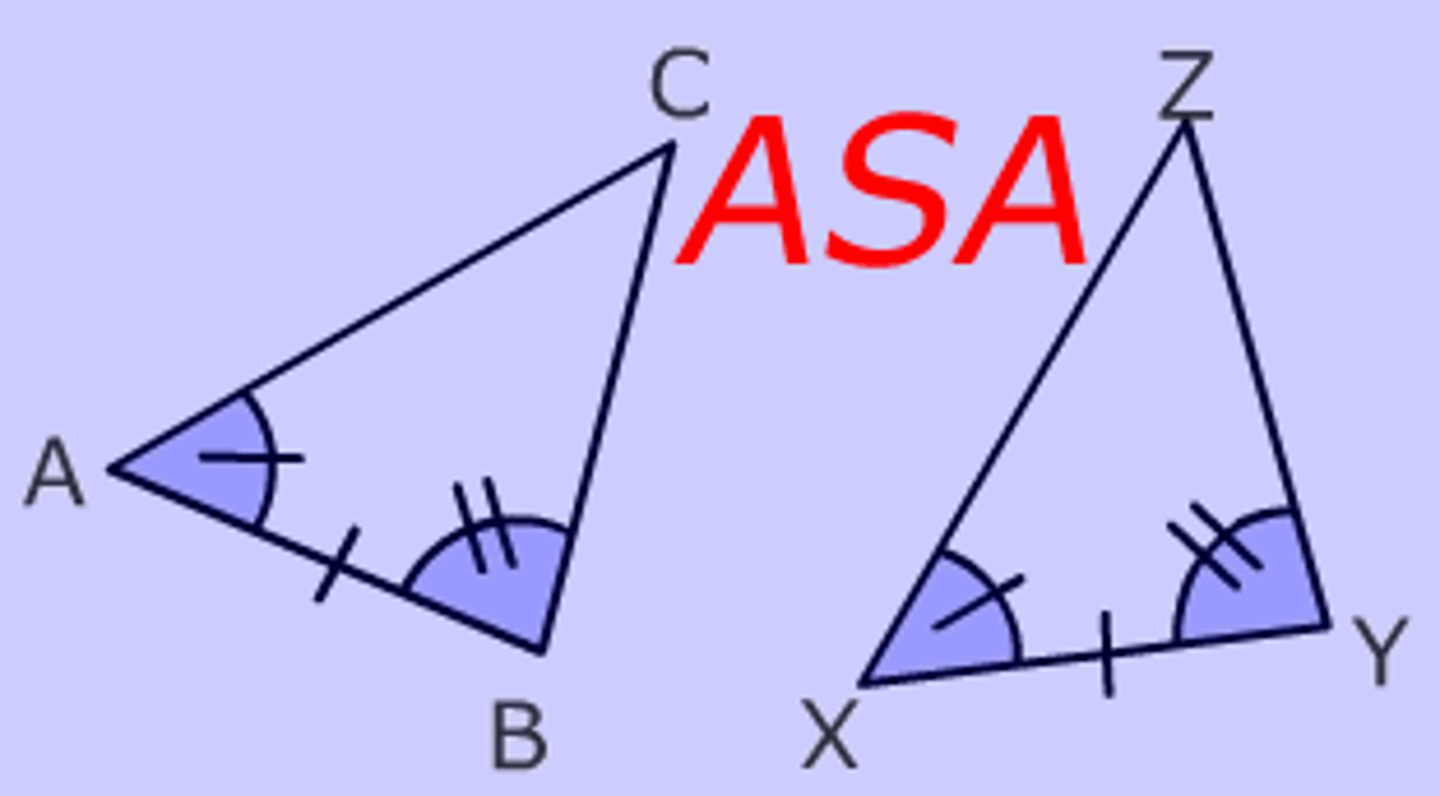
U4/5: Angle-Side-Angle (ASA) Postulate

If two pairs of angles and the angle between them of one triangle are congruent to the same parts in another triangle, then the triangles are congruent.

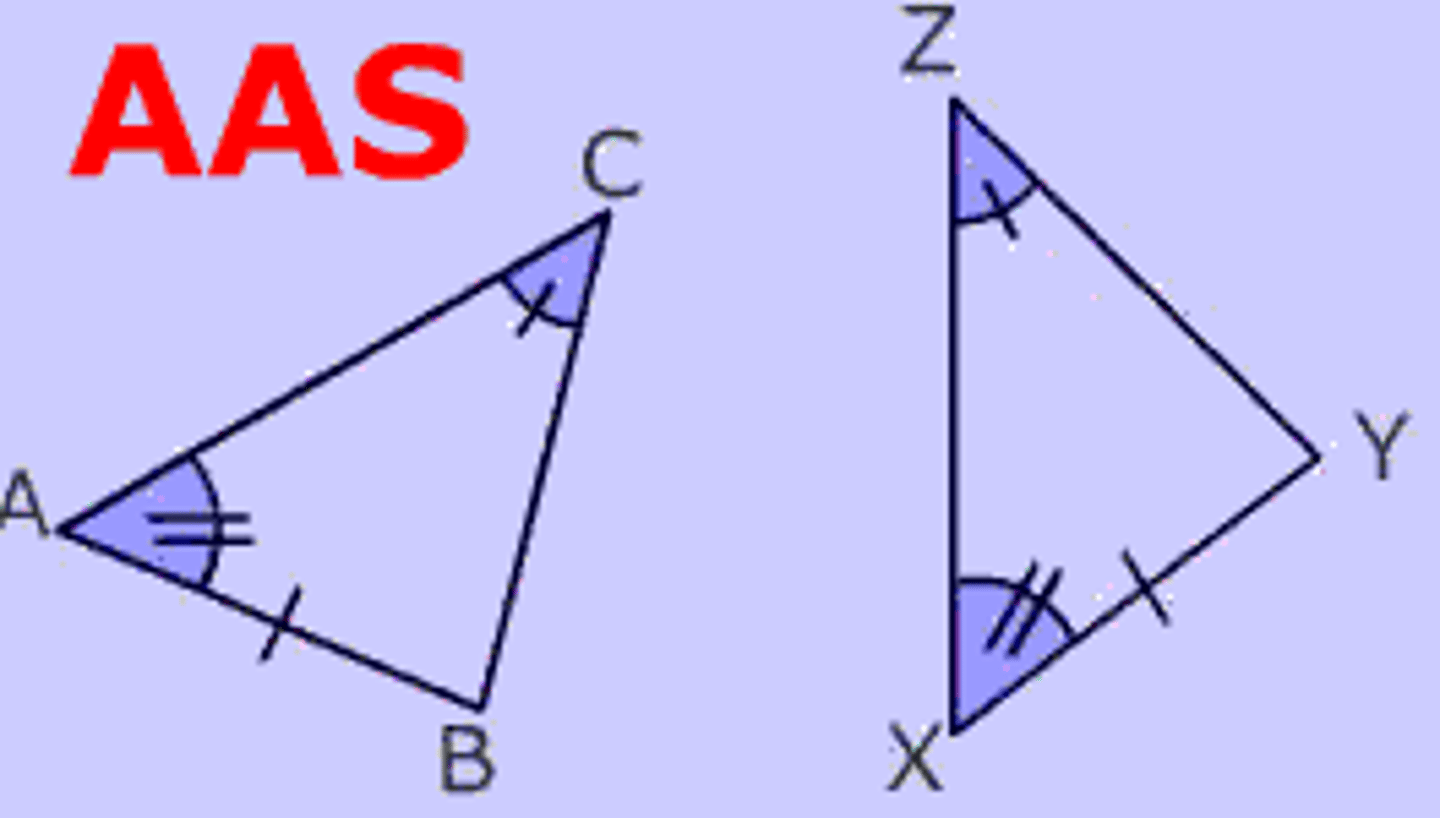
U4/5: Angle-Angle-Side (AAS) Postulate

If two angles and a non included side of one triangle are congruent to the corresponding two angles and non insured side of another triangle, then the two triangles are congruent.

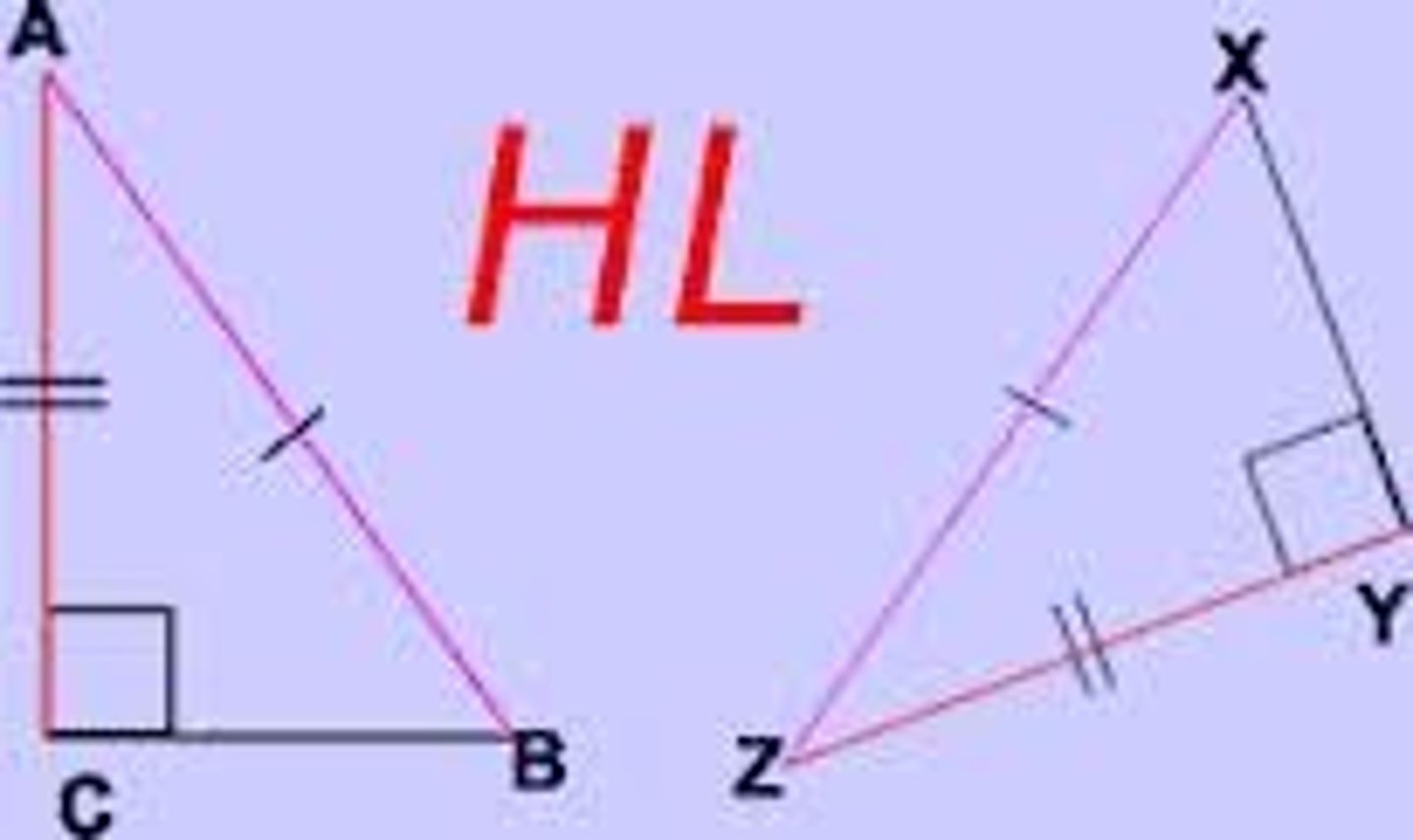
U4/5: Hypotenuse-Leg (HL) Theorem

If 2 triangles have a right angle, a congruent leg, and a congruent hypotenuse, then the 2 triangles are congruent.

—> you MUST show the triangles are right in order to use it

U4/5: CPCTC

Corresponding parts of congruent then triangles are congruent.

-parts = angles or sides

—> only used for parts not triangles

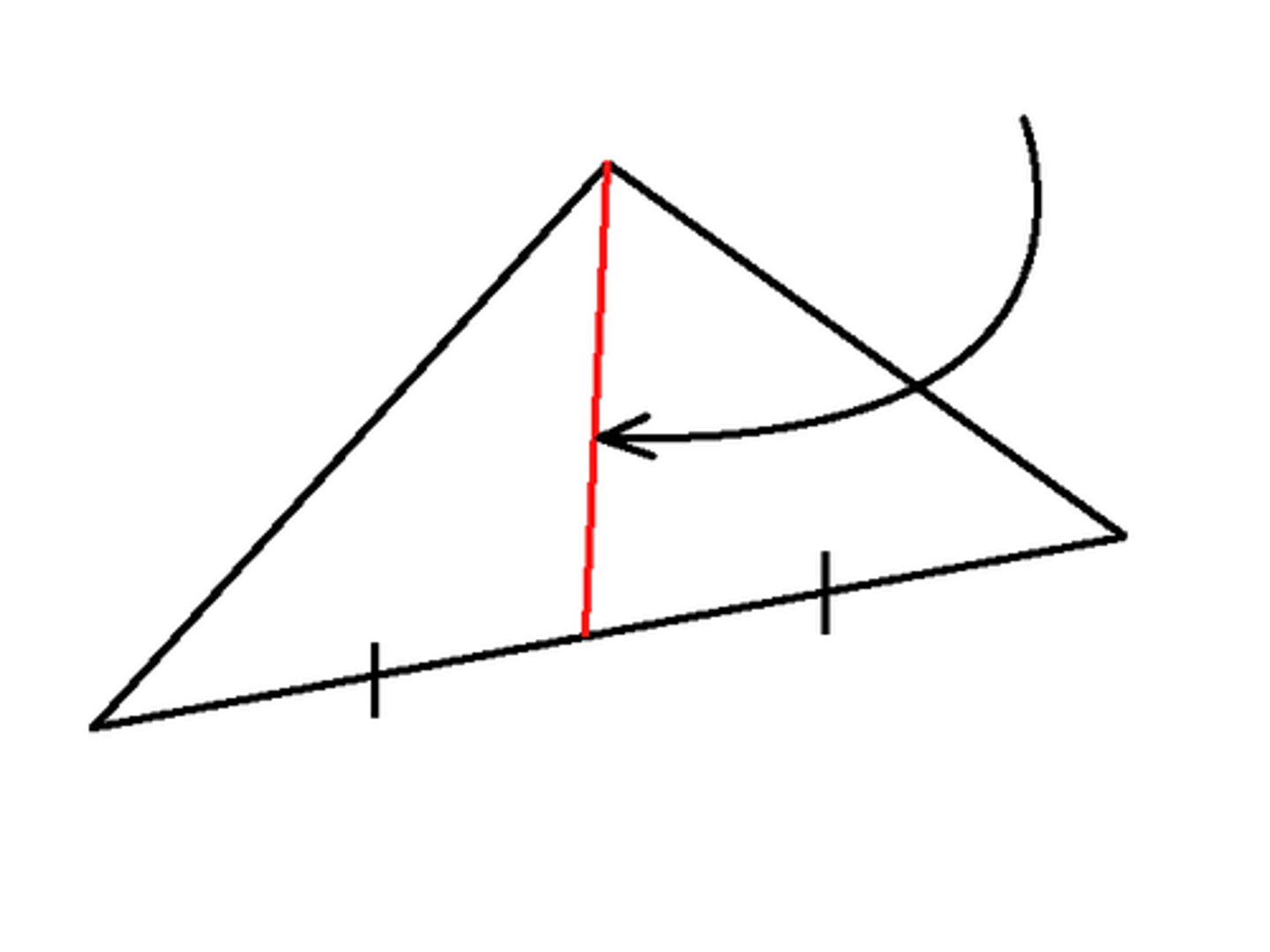
U4/5: Median

"Middle"

The median of a triangle is a segment from one vertex to the opposite midpoint.

U4/5: Formula for the area of a triangle

(height x base)/2

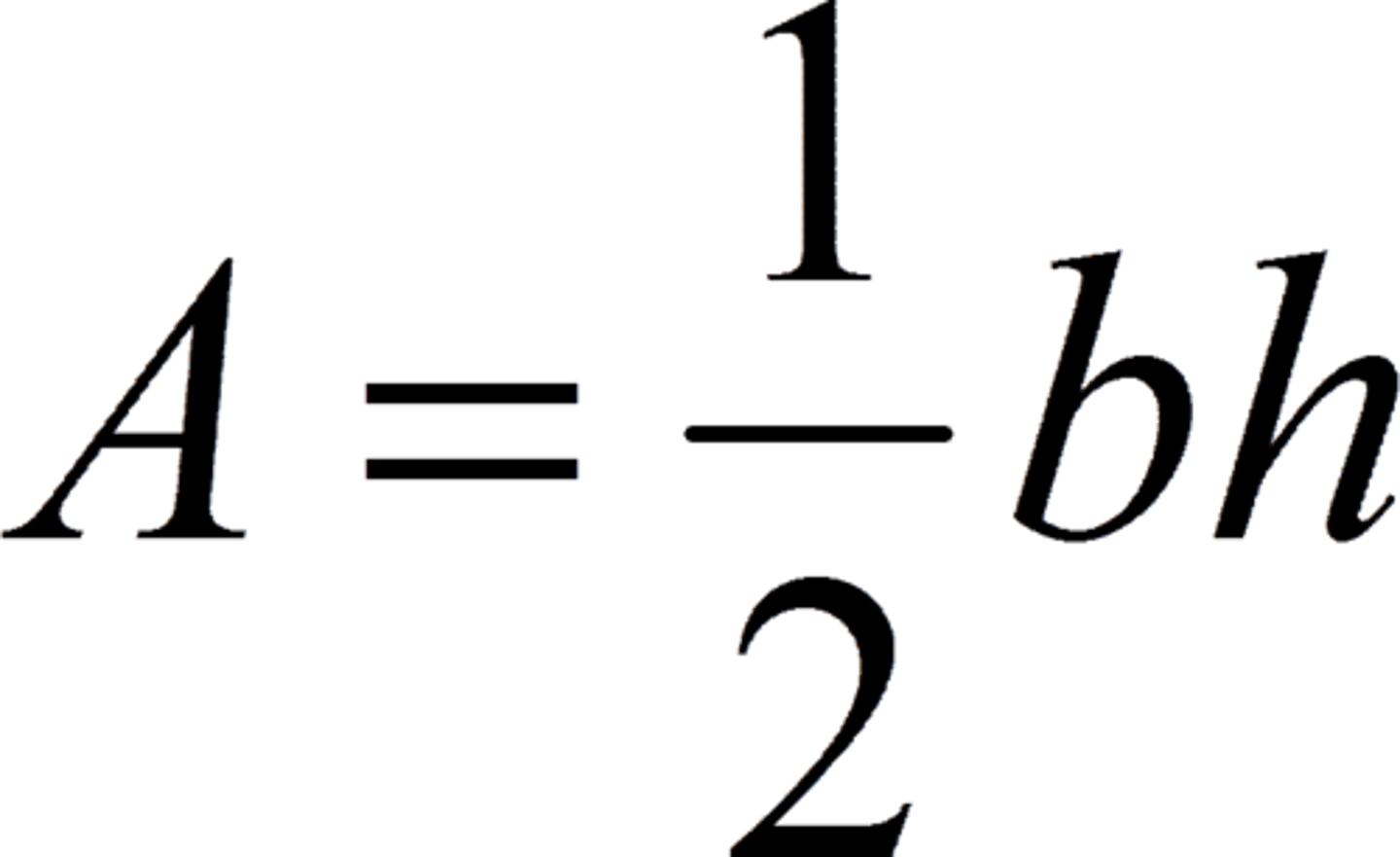
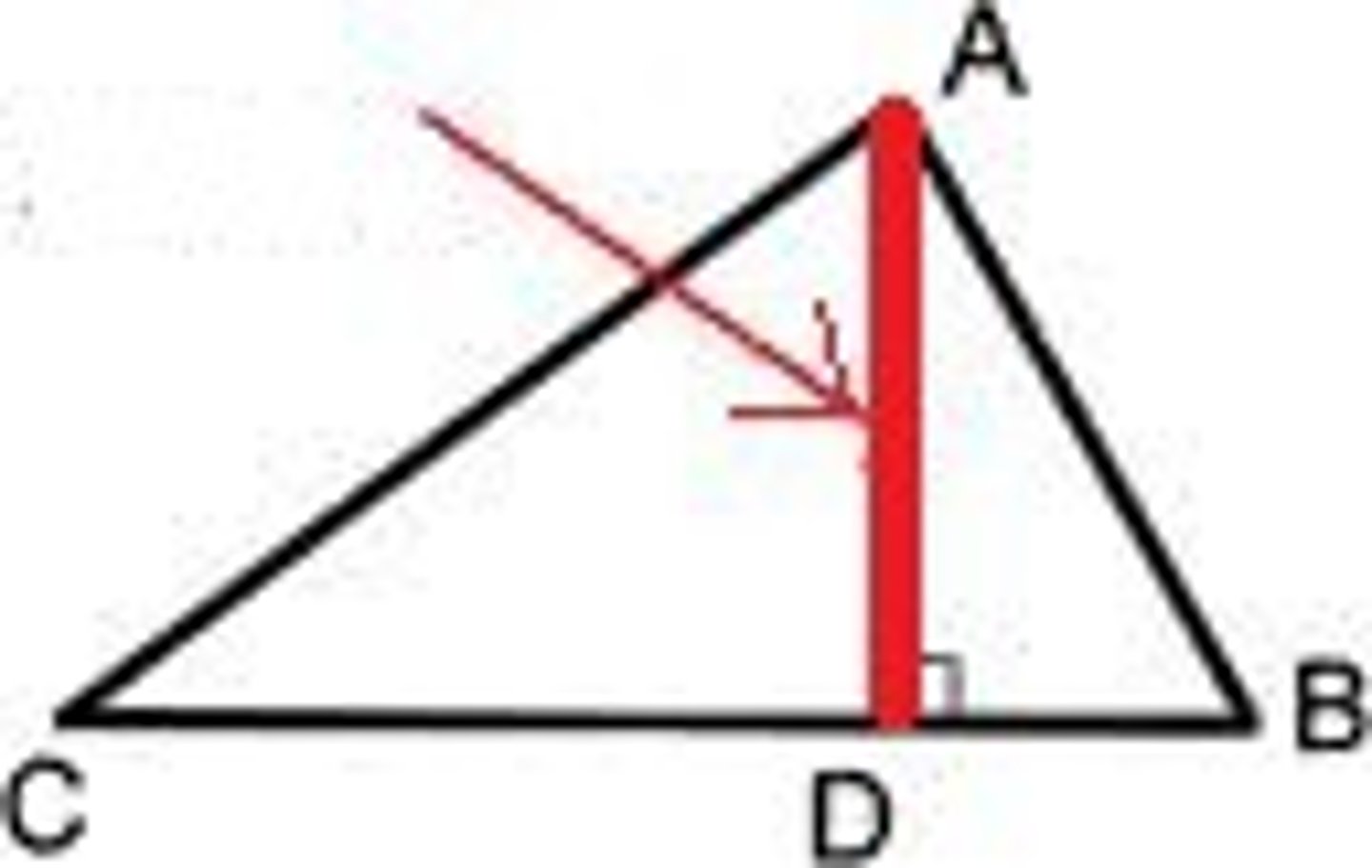
U4/5: Altitude

Height of something (triangle)

-height is always perpendicular to the base

-obtuse triangle = height is outside

-acute triangle= height inside

U4/5: Isoceles Triangle Theorem

If 2 sides of a triangle are congruent then the 2 opposite/across angles are congruent

U4/5: Isosceles Triangle Theorem Converse

If 2 angles are congruent then the 2 opposite of a triangle are congruent

U4/5: Perpendicular Bisector Theorem

If a point lies on the perpendicular bisector of a segment, then it is equidistant from the 2 endpoints of the segment.

U4/5: Converse of perpendicular bisector

If a point is equidistant from 2 end points of a segment then it is a perpendicular bisector.

U4/5: Angle bisector theorem

If a point lies in the angle bisector of an angle then it is equidistant from the 2 rays of the angle.

U4/5: How to be add or subtract segements or angles without converting to measures first?

We can use the Addition/subtraction postulates (not converting to the "measure of" before adding/subtracting) This is a shortcut and it not TECHNICALLY right but it okay for the midterms, tests, and regents.

U4/5: For three segments to form a triangle...

each side length must be less than the sum of the other 2 sides, but we only need to check the longest side (2 sides need to add to more than the longest side)

U4/5: In triangles the longest side must be...

greater than the sum of the other 2 sides

|y-z| < x < y+x

(Assuming x is the largest, assuming x is the smallest)

U4/5: the smallest angle is opposite the ______________angle and the largest angle is opposite the _____________ angle.

The largest angle is opposite the longest side.

The smallest angle is opposite the smallest side.

(angle is smaller, side is smaller, angle is larger, the side it larger)

U4/5: What are the three a^2+b^2 equations? and for what triangles?

a^2+b^2 a= c^2 (right triangle)

a^2+b^2 > c^2 (actute triangle)

a^2+b^2 < c^2 (obtuse triangle)

U4/5: Is SSA enough to prove congruence? AAA?

No, multiple triangles can be made. (THINK: ASS)

No, AAA will create SIMMILAR triangles, NOT CONGRUENT TRIANGLES

U4/5: If two angles are congruent and supplementary they just both be ________ angles

Right

U4/5: How to do quadatic equations

Combine like terms, Make one side equal zero(quadratic), then factor and use zero product property