Work and Heat. Internal Energy Physical Chemistry

Work of Expansion

W_surr=mgh=(mg/A)=Ah=P_ex∆V

(mg/A) = P_external

Ah= ∆V

W_sys=-W_surr=-P∆V

W_sys=-P∆V

Sign Conventions W_sys<0 expansion, W_sys>0 contraction, W=0 ∆V=0 work of expansion is 0

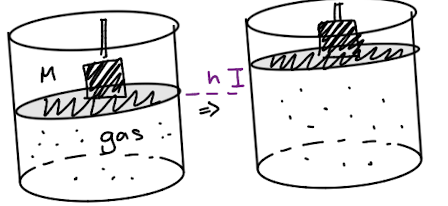
Quasistatic process

also known as a quasi-equilibrium process

a thermodynamic process that occurs slowly enough for the system to remain in internal thermodynamic equilibrium.

Quasistatic expansion and maximum work

Force of the gas is initially slightly larger than the force external

P_ex≤ P_gas

W_surr=P_ex∆V≤P_g∆V → maximum when P_gas=P_ex

(W_surr)_max=P_gas∆V

(W_surr)_rev=P∆V

W_rev=-P_sys∆V

Reversible work of expansion = work in a quasistatic process

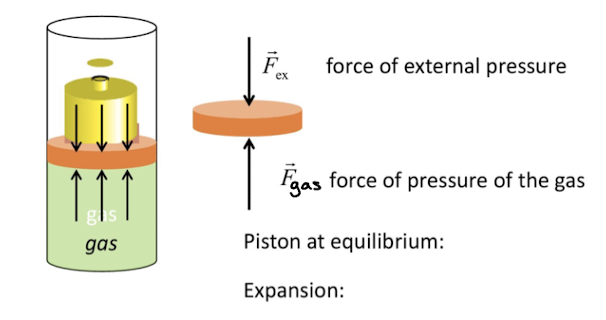
Isothermal quasistatic expansion of an ideal gas

every word matters for the application of this formula

ideal gas: PV=nRT

∆W=-P_ex∆V=-P_eye∆V (b/c quasistatic)

Isothermal: thermal bath temp to maintain temperature, and allow heat energy to maintain expansion.

Due to P vs V graph differentials taken to form final equation

Volume is a true differential due to it being a state funtion where as work is not a state function.

W_rev= -nRT x In (V_f/V_i)

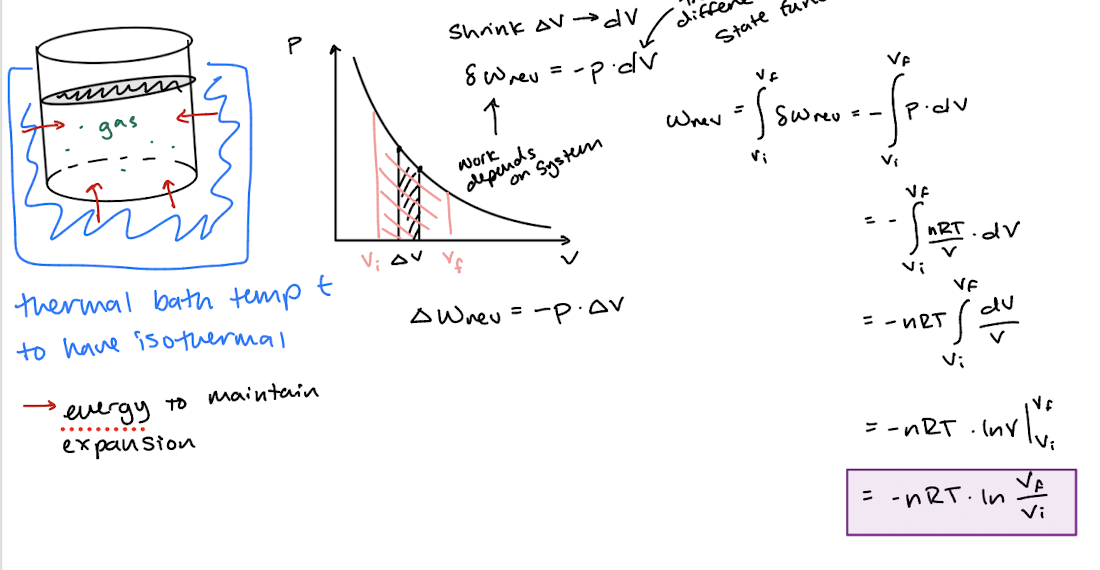
Work produced in chemical reactions

Chemical reactions can also release energy in the form of heat, or work, or both.

Not considered isothermal even if temperature is held constant due to it being a chemical reaction rather than a physical process

The measurement of heat

Heat capacity is heat absorbed by the system that raises its temperature by 1K (or 1˚C)

C=(q/∆t) units: J/K or J/˚C (extensive depends on the amount of substance)

intensive does not depend on the amount of substance (tabulated)

Specific Heat Capacity: C_s=(q/m∆T) units: J/KgK

Molar Heat Capacity: C_m=(q/n∆T) units: J/molK

Heat Capacity depends on the process in which the system recieves heat.

Constant V: C_mv=C_v= (q_v/n∆T) heat added at constant V

Constant P: C_mp=C_p=(q_p/n∆T) heat added at constant P