PSTAT 160A ichiba

Given a random variable X, define the moment generating function

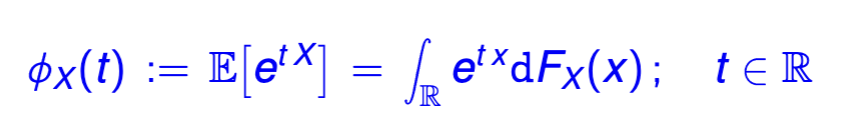
if X and Y are independent, how does the MGF_X+Y(•) simplify?

MGF_X(•) • MGF_Y(•)

similarly E(e^t(x+y)) = E(e^tx) • E(e^ty)

obtain the mgf by differentiating

what is the power/taylor series defined as?

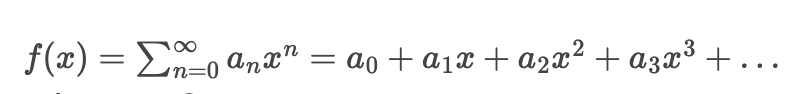
define the probability generating function

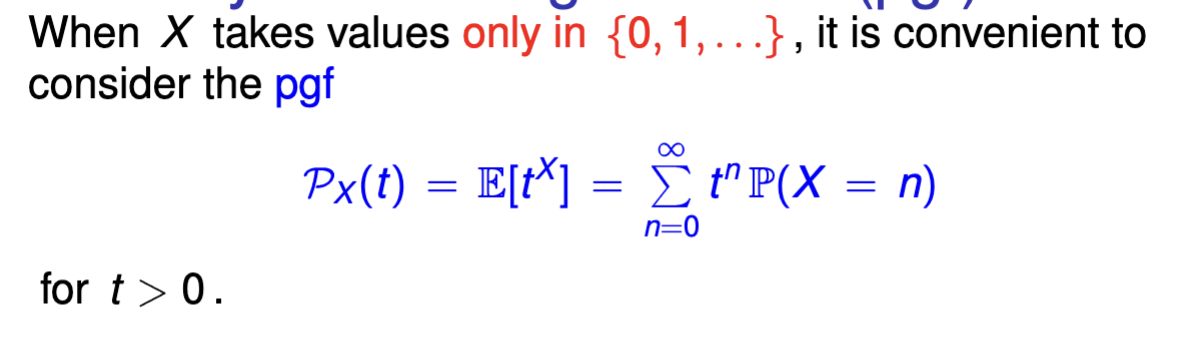
what is the formula for turning the PGF into a probability formula?

This process proves that the PGF and the probability distribution contain the exact same information. If PX​(t) is identical to PY​(t), then decoding them will produce the exact same set of probabilities. Therefore, X and Y must be identically distributed.

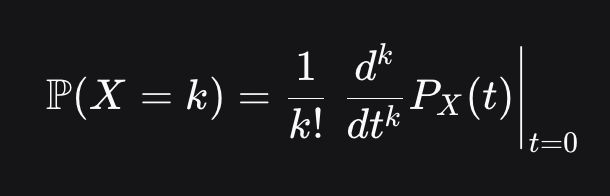
what is the reflection principle

when is a random walk transient?

when P(S_n = a infiinitely often in n) = 0

• might visit “a” a few times but eventually it will leave and never return

• returns to “a” a finite number of times

when is a random walk recurrent?

when P(S_n = a infinitely often in n) = 1

• guaranteed to return to “a” over and over again forever

what is the formula for a symmetric random walk and the properties of symmetric random walk?

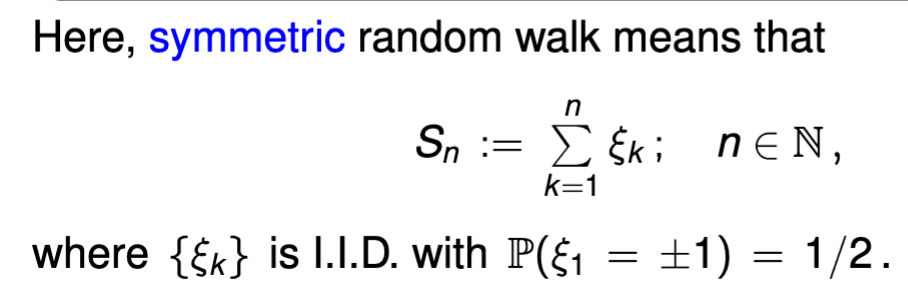
what is τ?

τ is a stopping time, a random time where the random walk decides to stop at time n and depends only on the info up to time n and not the future .

when does the reflection decide to reflect in a random sample walk?

at time τ

where does the sample walk decide to reflect?

at M_n = maxS_l (the “y” value where the reflection starts and reflects over)

write the proof that states {^S_n} is the symmetric random walk:

what is the central limit theorem?

No matter what distribution you start with, if you take the average of enough independent samples, it will look like a normal distribution.