Quarterly exam 1 marks

The equation of the locus of the point whose distance from y – axis is half the distance from origin is

(4) 3x² – y² = 0

Which of the following equation is the locus of (at², 2at)

(4) y² = 4ax

Which of the following points lie on the locus of 3x² + 3y² – 8x – 12y + 17 = 0

(3) (1, 2)

If the point (8, – 5) lies on the focus x²/16−y²/25 = k, then the value of k is

(4) 3

Straight line joining the points (2, 3) and (- 1, 4) passes through the point (α, β) if

(3) α + 3β = 11

The slope of the line which males an angle 45°with the line 3x – y = – 5 are

(2) 1/2, – 2

Equation of the straight line that forms an isosceles triangle with coordinate axes in the 1-quadrant with perimeter 4 + 2√2 is

(2) x + y – 2 = 0

The coordinates of the four vertices of a quadrilateral are (-2, 4), (-1, 2), (1, 2) and (2, 4) taken in order. The equation of the line passing through the vertex (-1, 2 ) and dividing the quadrilateral in the equal areas is

(4) x – y + 3 = 0

The intercepts of the perpendicular bisector of the line segment joining (1,2) and (3,4) with coordinate axes are

(2) 5, 5

The equation of the line with slope 2 and the length of the perpendicular from the origin equal to √5 is

(3) 2x - y = 5

If a line is perpendicular to the line Sx-y = 0 and forms a triangle with the coordinate axes of area 5 sq. units, then its equation is

(1) x + 5y ± 5√2 = 0

Equation of the straight line perpendicular to the line x – y + 5 = 0 through the point of intersection y-axis and the given line

(2) x + y – 5 = 0

If the equation of the base opposite to the vertex (2, 3) of an equilateral triangle is x + y = 2, then the length of a side is

(3) √6

The line (p + 2q)x + (p – 3q)y = p – q for different values of p and q passes through the point

(4) (2/5,3/5)

The point on the line 2x – 3y = 5 is equal distance from (1, 2), and (3, 4) is

(2) (4, 1)

The image of the point (2, 3) in the line y = -x is

(1) (- 3, – 2)

The length of perpendicular from the origin to the line x/3−y/4 = is

(3) 12/5

The y – intercept of the straight line passing through (1, 3) and perpendicular to 2x – 3y + 1 = 0 is

(2) 9/2

If the two straight lines x + (2k – 7)y + 3 = 0 and 3kx + 9y – 5 = 0 are perpendicular, then the value of k is

(1) k = 3

If a vertex of a square is at the origin and it’s one side lies along the line 4x + 3y – 20 = 0
then the area of the square is

(2) 16 sq. units

If the lines represented by the equation 6x² + 41xy – 7y² = 0 make angles α and β with x-axis then tan α . tan β =

(1) –6/7

The area of the triangle formed by the lines x² – 4y² = 0 and x = a is

(3) ½ a²

If one of the lines given by 6x² – xy – 4cy² = 0 is 3x + 4y = 0,then c equals to

(1) -3

θ is acute angle between the lines x² – xy – 6y² = 0 then 2cosθ+3sinθ / 4cosθ+5cosθ

(3) 5/9

The equation of one of the lines represented by the equation x² + 2xy cot θ – y² = 0 is

(4) x sin θ + y(cos θ + 1) = 0

The value of 2 + 4 + 6 + …………… + 2n is

(4) n(n + 1)

The coefficient of x⁶ in (2 + 2x)¹⁰ is

(4) 10C₆2¹⁰

The coefficient of x⁸ y¹² in the expansion of (2x + 3y)²⁰ is

(4) 20C₈ 2⁸ 3¹²

If nC₁₀ > nC_r for all possible r then a value of n is

(4) 20

If a is the Arithmetic mean and g is the Geometric mean of two numbers then

(2) a ≥ g

If (1 + x²)² (1 + x)ⁿ = a₀ + a₁x + a₂x² + ………… + x^{n + 4} and if a₀, a₁, a₂ are in A. P then n is

(3) 2

If a, 8, b are in A .P , a, 4 , b are in G. P and if a, x ,b are in H . P then x is

(1) 2

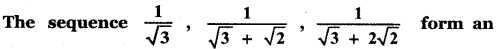
(3) H.P

The H.M of two positive numbers whose A.M and G.M are 16,8 respectively is

(4) 4

If S denote the sum of n terms of an A. P whose common difference is d, the value of S_n – 2S_{n- 1} + S_{n – 2} is

(1) d

The remainder when 38¹⁵ is divided by 13 is

(1) 12

The nth term of the sequence 1, 2, 4, 7, 11, ………….. is

(4) n2−n+2/2

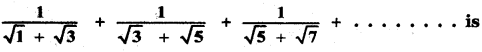
The sum up to n terms of the series

(4) √2n+1−1 /2

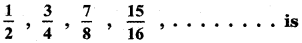
The n^th term of the sequence

(2) 1 – 2^-n

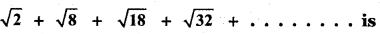
The sum up to n terms of the series

(3) n(n+1)/√2

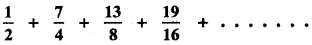
The value of the series

(1) 14

The sum of an infinite G.P is 18. If the first term is 6 the common ratio is

(2) 2/3

The coefficient of x⁵ in the series e^-2x is

(3) −4/15

The value of

(3) (e−1)²/2e

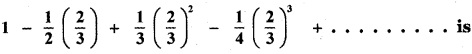
The value of

(2) 3/2 log (5/3)

The sum if the digits at the 10^th place of all numbers formed with the help of 2, 4, 5, 7 taken all at a time is
(1) 432
(2) 108
(3) 36
(4) 18

(2) 108

In an examination, there are three multiple-choice questions and each question has 5 choices. The number of ways in which a student can fail to get all answer correct is
(1) 125
(2) 124
(3) 64
(4) 63

(2) 124

The number of ways in which the following prize be given to a class of 30 boys first and second in mathematics, first and second in Physics, first in Chemistry and first in English is
(1) 30⁴ × 29²
(2) 30² × 29³
(3) 30² × 29⁴
(4) 30 × 29⁵

(1) 30⁴ × 29²

The number of 5 digit numbers all digits of which are odd is
(1) 25
(2) 5⁵
(3) 5⁶
(4) 625

(2) 5⁵

In 3 fingers, the number of ways four rings can be worn is ————- ways.
(1) 4³ – 1
(2) 3⁴
(3) 68
(4) 64

(2) 3⁴

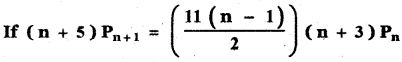
then the value of n are
(1) 7 and 11
(2) 6 and 7
(3) 2 and 11
(4) 2 and 6

(2) 6 and 7

The product of r consecutive positive integers is divisible by
(1) r !
(2) (r – 1) !
(3) ( r + 1 ) !
(4) r^r

(1) r !

The number of five-digit telephone numbers having at least one of their digits repeated is
(1) 90000
(2) 10000
(3) 30240
(4) 69760

(4) 69760

If (a² – a ) C₂ = ( a² – a) C₄ then the value of a is

(1) 2
(2) 3
(3) 4
(4) 5

(2) 3

There are 10 points in a plane and 4 of them are collinear. The number of straight lines joining any two points is
(1) 45
(2) 40
(3) 39
(4) 38

(2) 40

The number of ways in which a host lady invite for a party of 8 out of 12 people of whom two do not want to attend the party together is
(1) 2 × 11C₇ + 10C₈
(2) 11C₇ + 10C₈
(3) 12C₈ – 10C₆
(4) 10C₆ + 2!

(3) 12C₈ – 10C₆

The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines.
(1) 6
(2) 9
(3) 12
(4) 18

(4) 18

Everybody in a room shakes hands with everybody else. The total number of shake hands is 66. The number of persons in the room is
(1) 11
(2) 12
(3) 10
(4) 6

(2) 12

Number of sides of a polygon having 44 diagonals is

(1) 4

(2) 4!

(3) 11

(4) 22

(3) 11

If 10 lines are drawn in a plane such that no two of them are parallel and no three are concurrent, then the total number of point of intersection are
(1) 45
(2) 40
(3) 10!
(4) 210

(1) 45

In a plane there are 10 points are there out of which 4 points are collinear, then the number of triangles formed is
(1) 110
(2) 10C₃
(3) 120
(4) 116

(4) 116

In 2nC₃ : nC₃ = 11 : 1 then
(1) 5
(2) 6
(3) 11
(4) 7

(2) 6

(n – 1) C_r + ( n – 1 ) C_{r – 1} is
(1) (n + 1) C_r
(2) (n – 1) C_r
(3) nC_r
(4) nC_{r – 1}

(3) nC_r

The number of ways of choosing 5 cards out of a deck of 52 cards which include atleast one king is
(1) 52C₅
(2) 48 C₅
(3) 52C₅ + 48C₅
(4) 52C₅ – 48C₅

(4) 52C₅ – 48C₅

The number of rectangles that a chessboard has
(1) 81
(2) 9⁹
(3) 1296
(4) 6561

(3) 1296

The number of 10 digit number that can be written by using digits 2 and 3 is
(1) 10C₂ + 9C₂
(2) 2¹⁰
(3) 2¹⁰ – 2
(4) 10!

(2) 2¹⁰

If Pr stands for rPr, then the sum of the series 1 + P₁ + 2P₃ + 3P₃ + ……… + nP_n is
(1) P_{n + 1}
(2) P_{n + 1} – 1
(3) P_{n + 1} + 1
(4) (n + 1)P_{n – 1}

(2) P_{n + 1} – 1

The product of first n odd natural numbers equals
(1) 2nC_n × nP_n
(2) (1/2)n 2nC_n × nP_n
(3) (1/4)n × 2nC_n × 2nP_n
(4) nC_n × nP_n

(2) (1/2)n 2nC_n × nP_n

If nC₄, nC₅, nC₆ are in A. P. the value of n can be
(1) 14
(2) 11
(3) 9
(4) 5

(1) 14

1 + 3 + 5 + 7 + …………. + 17 is equal to
(1) 101
(2) 81
(3) 71
(4) 61

(2) 81

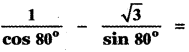
(1) √2
(2) √3
(3) 2
(4) 4

(4) 4

If cos 28° + sin 28°= k³, then cos 17° is equal to

(1) k³/2√
(2) −k³/2√
(3) ±k³/2√
(4) −k³/3√

(1) k³/2√

The maximum value of 4 sin²x + 3 cos²x + sin + cos is

(1) 4 + √2
(2) 3 + √2
(3) 9
(4) 4

(1) 4 + √2

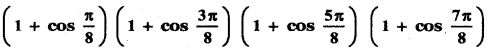
(1) 1/8
(2) 1/2
(3) 1/√3
(4) 1/√2

(1)1/8

If π < 2θ < 3π2,√ 2+√ 2+2cos4θ equals to

(1) – 2 cos θ
(2) – 2 sin θ
(3) 2 cos θ
(4) 2 sin θ

(4) 2 sin θ

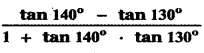
If tan 40° = λ, then

(1) 1−λ²/λ
(2) 1+λ²/λ
(3) 1+λ²/2λ
(4) 1−λ²/2λ

(4) 1−λ²/2λ

cos 1° + cos 2° + cos 3° + ….. + cos 179° =

(1) 0
(2) 1
(3) – 1
(4) 89

(1) 0

Let f_k(x) = 1/k[sin^kx + cos^kx] where x ∈ R and k ≥ 1. Then f₄(x) – f₆(x) =

(1) 1/4
(2) 1/12
(3) 1/6
(4) 1/3

(2) 1/12

Which of the following is not true?
(1) sin θ = – 3/4
(2) cos θ = – 1
(3) tan θ = 25
(4) sec θ = 1/4

(4) sec θ = 1/4

cos 2θ cos 2Φ + sin²(θ – Φ) – sin²(θ + Φ) is equal to
(1) sin 2 (θ + Φ)
(2) cos 2 (8 + Φ)
(3) sin 2 (θ – Φ)
(4) cos 2(θ – Φ)

(2) cos 2 (8 + Φ)

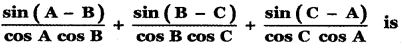
(1) sin A + sin B + sin C
(2) 1
(3) 0
(4) cos A + cos B + cos C

(3) 0

If cos pθ + cos qθ = o and if p ≠ q then θ is equal to(n is any integer)

(1)

(2)

(3)

(4)

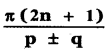
If tan α and tan β are the roots of x² + ax + b = 0 then sin(α+β)/sinαsinβ is equal to
(1) b/a
(2) a/b
(3) –a/b
(4) –b/a

(3) –a/b

In a triangle ABC, sin² A + sin² B + sin² C = 2 then the triangle is .
(1) equilateral triangle
(2) isosceles triangle
(3) right triangle
(4) scalene triangle

(3) right triangle

If f(θ) = |sin θ| + |cos θ|, θ ∈ R then f(θ) is in the interval
(1) [0, 2]
(2) [1, √2]
(3) [1, 2]
(4) [0, 1]

(2) [1, √2]

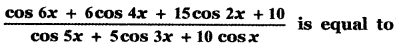
(1) cos 2x
(2) cos x
(3) cos 3x
(4) 2 cos x

(4) 2 cos x

The triangle of the maximum area with a constant perimeter of 12m
(1) is an equilateral triangle with a side of 4m
(2) is an isosceles triangle with sides 2m, 5m, 5m
(3) is a triangle with sides 3m, 4m, 5m
(4) does not exist.

(1) is an equilateral triangle with a side of 4m

A wheel is spinning at 2 radians/second. How many seconds will it take to make 10 complete rotations?
(1) 10 π seconds
(2) 20 π seconds
(3) 5 π seconds
(4) 15 π seconds

(1) 10 π seconds

If sin α + cos α = b, then sin 2α is equal to
(1) b² – 1, if b ≤ √2
(2) b² – 1, if b > √2
(3) b² – 1, if b ≥ √2
(4) b² – 1, if b < √2

(1) b² – 1, if b ≤ √2

In an ∆ABC
(i) sin A/2 sin B/2 sin C/2 > 0
(ii) sin A sin B sin C > 0,then
(1) Both (i) and (ii) are true
(2) only (1) is true
(3) only (ii) Is true
(4) neither (i) nor (ii) is true

(1) Both (i) and (ii) are true

If |x + 2| ≤ 9, then x belongs to

[−11, 7]

Given that x, y and b are real numbers x < y, b > 0, then

xb

If |x − 2| / x − 2 ≥ 0, then x belongs to

(2, ∞)

The solution of 5x − 1 < 24 and 5x + 1 > −24 is

(−5, 5)

The solution set of the following inequality |x − 1| ≥ |x − 3| is

[2, ∞)

The value of log√2 512 is

18

The value of log3 1/81 is

-4

If log√x 0.25 = 4, then the value of x is

0.5

The value of loga b logb c logc a is

1

If 3 is the logarithm of 343, then the base is

7