Binary + Numbers

Simplicity

Focus the computer hardware on handling small, positive whole numbers

• Our objective is to design low-cost effective hardware

• Need to design it as simple as possible

Any other data type is just a code (or “representation”, or “interpretation”) that maps to positive whole numbers 2 

ASCII (American Standard Code for Information Interchange)

Widely-used code for characters

Defines 128 symbols (7-bit binary code )

e.g., the letters A,B,…,H,...Z are represented as 65,66,…,72,…90

Multiplying by the Radix (denary)

• To multiply by 10, we shift left by one place

• To divide by 10, we shift right by one place

Note the general principle here: to multiply or divide by radix ^n , we shift n places:

• For positive n (multiplication), we shift left by n places

• For negative n (division), we shift right

•  by n places

Infinite and Finite Precision

Given any two integers i and j, we normally (i.e., in everyday life) assume that i + j, i - j, and i x j will always generate a valid (integer) result

• the underlying assumption is that the range of integers is infinite

What does Finite Precision lead to?

arithmetic overflow, if the result is too big to store

Sign and Magnitude Drawbacks

1. We sacrifice a column for the sign indicator (called flag)

2. We get two representations of zero 

Both positive and negative 0. messy: when we have to test for zero, we must do it twice! Complicates hardware and/or software

Excess n

We use what was the “sign” column to represent a so-called excess

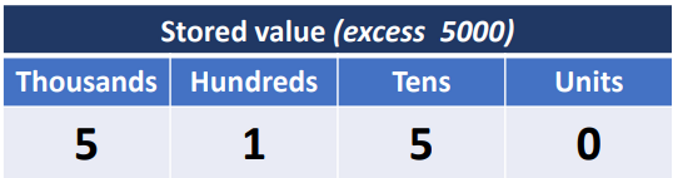
Best introduced by example: code the number 150 using four decimal columns

• We can do this using “excess 5000”: put a 5 in the thousands, column

We code (i.e. store) a number by adding the excess to it

• Ensures that negative value numbers get coded as positive value

We decode a representation by subtracting the excess from it

Properties of Excess n Compared to Sign and Magnitude

• We have regained a storage slot

• We no longer have two representations of 0

• We can represent more numbers:

  • 4 bit sign and magnitude can represent 10^3 numbers

  • 4 bit excess n can represent 0-9999: half for negative value, half for positive value

Choosing the value of n (Excess n)

Why did we choose excess 5000 in our examples?

• n was half the number of values available: i.e. 10000/2

Can also be seen as a function of the number of columns

Problems with Fixed Point

Quickly run out of columns

Let’s say we use 8 columns for numbers (base-10), and reserve half of these columns for fractional parts: 

• The usable range (i.e. integer part) is ~ ± 5000 (with excess n, n=5000=10^4/2)

Then, how do we express planetary distance, or similarly very large numbers?

• Trade precision for range:

  • For very small numbers we generally talk of numbers ‘to n decimal places’

  • So except finance etc we can often approximate values, and trade accuracy for range

Floating Point

Represents the mantissa and exponent as separate fixed-point numbers

• Normalise by putting the first non-0 mantissa digit in the leftmost column

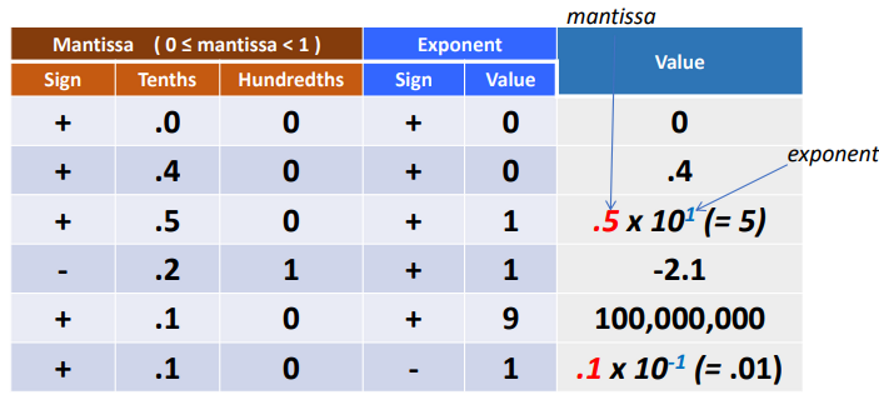
Mantissa

value

Exponent

what the mantissa is multiplied by

Octal

• Base 8

• 0-7

• Can be represented by splitting binary into sets of 3 as 8 is 2^3

Hexadecimal

• Base 16

• 0-9,A-F

• Can be represented by splitting binary in to groups of 4 as 16 is 2^4

Problem with Excess n

x - y != x + (-y)

• Need extra hardware (for subtraction as well as addition)

Two’s Compliment Methods for Negative Number

• starting with the equivalent positive number

• inverting (or flipping) all bits – changing every 0 to 1, and every 1 to 0

• adding 1 to the entire inverted number, ignoring any overflow

IEEE 754 Floating Point

The standard floating point representation used by almost all modern computers

Mantissa is coded using sign and magnitude

• Although we don't store the MSB

Exponent is coded in excess n

• For an exponent held in b bits, n = (2b − 1) − 1 

• So, use excess 127 for an 8-bit exponent

There are multiple formats available for different “precisions”: half, single, double, quadruple

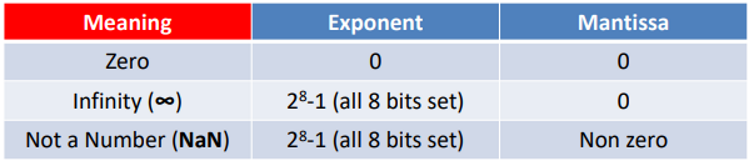
Special Values in IEEE 754

Some bit patterns never appear so we can use them to indicate special cases such as:

NaN is used to indicate results for which there is no valid outcome, e.g. as division by 0

Equality Testing

With numbers coded as floating point, we must never write code like this:

• If (x == y) {...} 

• OR: if (0.1 + 0.2 == 0.3) {...}

A possible rounding error resulting from lack of precision means that we can never be confident that two numbers that “should be” equal are actually coded as equal

Instead we should take a cautious approach:

• If (abs(x-y) < error_tolerance) {...}