Categorical and Propositional Logic

These flashcards cover key concepts and definitions from the lecture notes on categorical and propositional logic.

Categorical Proposition

A simple proposition that asserts the relationship between two classes of objects or concepts.

Subject

The term being predicated in relation to another category or concept.

Predicate

The term that predicates (defines/describes) the subject.

Universal Affirmative

Form A: A categorical proposition stating that all members of a subject class are included in a predicate class.

Universal Negative

Form E: A categorical proposition stating that no members of a subject class are included in a predicate class.

Particular Affirmative

Form I: A categorical proposition stating that some members of a subject class are included in a predicate class.

Particular Negative

Form O: A categorical proposition stating that some members of a subject class are not included in a predicate class.

Quantity

The extent to which the subject class refers to all or some members in a categorical proposition.

Quality

The affirmative or negative character of a proposition.

Copula

A linking verb ('are' or 'are not') that connects the subject and predicate.

Existential Import

The concept that the truth value of a proposition depends on the existence of the things to which it refers.

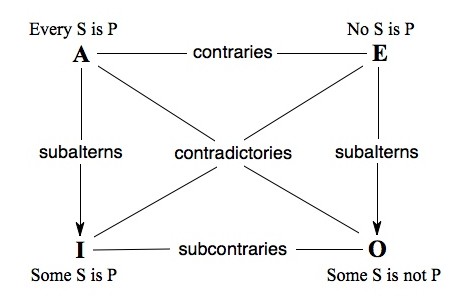
Contradictories

Propositions that cannot both be true or both be false.

• two propositions never share the same truth value.

Contraries

Pairs of propositions that cannot both be true but can both be false.

• A and E can’t both be true but may both be false.

Subcontraries

Pairs of propositions that cannot both be false but can both be true.

• I and O can’t both be false but may both be true

Subalterns

The relationship between a universal proposition and its corresponding particular proposition.

Categorical Syllogism

A deductive argument consisting of two premises and a conclusion, each being categorical propositions.

Major Term

The predicate in the conclusion of a categorical syllogism.

Minor Term

The subject in the conclusion of a categorical syllogism.

Middle Term

The term that connects the major and minor terms, appearing in both premises.

Mood and Figure

The mood is symbolized by the propositional forms, while the figure is determined by the position of the middle term in premises.

Propositional Logic

The logic of compound statements that focuses on propositions as its primary components.

Truth Functions

The relationships that determine the truth value of a compound statement based on its simple propositions.

Tautology

A statement that is always necessarily true.

Self-Contradiction

A statement that is always necessarily false.

Logical Equivalence

Two statements that have the same truth value in every scenario but not necessarily the same phrasing.

Square of Opposition

A graphical representation to highlight relationships between standard-form categorical propositions that differ in quality, quantity, or both.

• Universal statements have a truth value, even if their subject class is empty.

• Universal statements lack existential import: they can be framed as If-then statements.

• Particular statements inherently have existential import.