SEMMELWEIS UNIVERSITY Medical Biophysics I. Semifinal - Theory topics

Types of radiation

according to energy transfer: Electromagnetic (light), mechanical (sound), particle (alpha)

according to interaction with matter: ionizing (alpha), nonionizing (sound)

Dependance of irradiance on distance from the source

Irradiance is the incident radiation on a target. The dependence on distance from the source varies with the type of source. Assuming there is no attenuation:

● Point like source:​ irradiance is inversely proportional to the s​quared distance​from the source.

● Cylindrical source: irradiance is inversely proportional to the distance from the source.

● Planar source: irradiance does not change with increasing distance from the source (as long as the distance is increased perpendicular to the plane and is not greater than the linear size of the source)

If the distance from the source is not perpendicular: Ei=Einc,maxCosalpha

Fundamentals of geometric optics

When light propagates through slits which are much larger than its wavelength, we can consider the wavefront as a line. This simplification allows us to calculate optical imaging with relative ease.

Radiometric Quantities

Characterising the source:

Radiant power (W=J/s) P = ΔE/Δt

Radiant emittance and irradiance (W/ m2 )

M=ΔP/ΔA

Einc=ΔP/ΔA inc

Characterising the radiation:

Radiant flux (W=J/s) IE= ΔE Δt

Intensity JE = ΔIE/ΔA

Attenuation law

J=J0xe^-müx

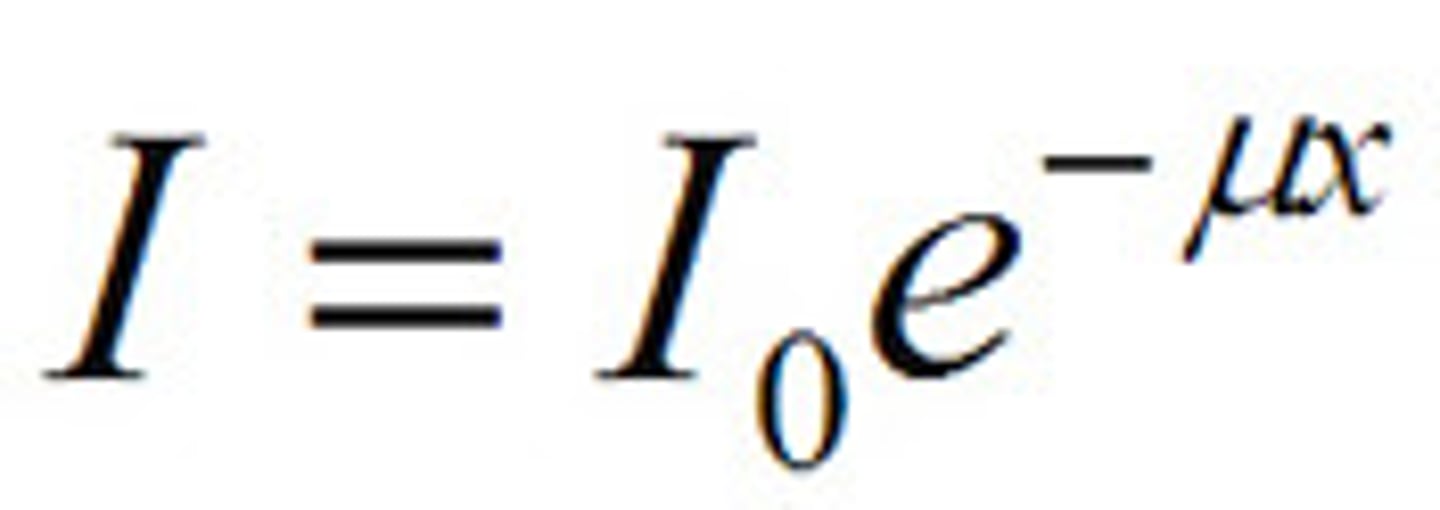
Fermat's Principle

Light will choose the path which takes the least amount of time (i.e spend the least amount of time in the slower medium). Is the basis for the phenomenon of refraction and reflection.

Law of Refraction (Snell's Law)

Incident and refracted ray together with the normal line (=optical axis) are all located on the same plane.

Snell's law: (sin alpha/sin beta) = c1/c2 = n21

Law of reflection.

Angle of incidence = angle of reflection

Incident beam, reflected beam and optical axis are in the same plane.

Total internal reflection and its applications.

Occurs when light is propagated from a higher refractive index thoward a medium with lower refr.index and with a larger angle than the critical angle. The critical angle is calculated by this formula: (1/sinBetac)= (n2/n1). Application: endoscopy

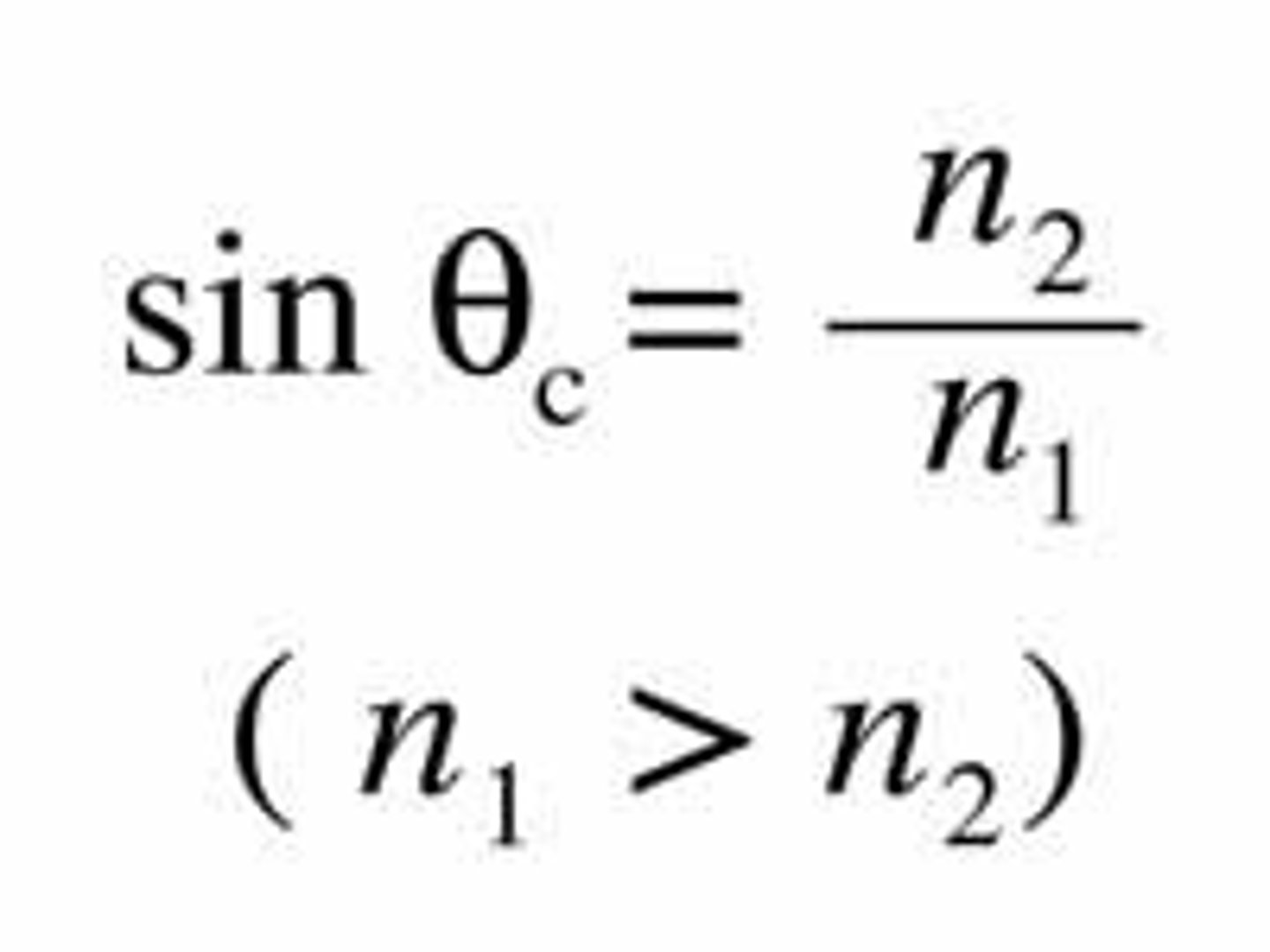
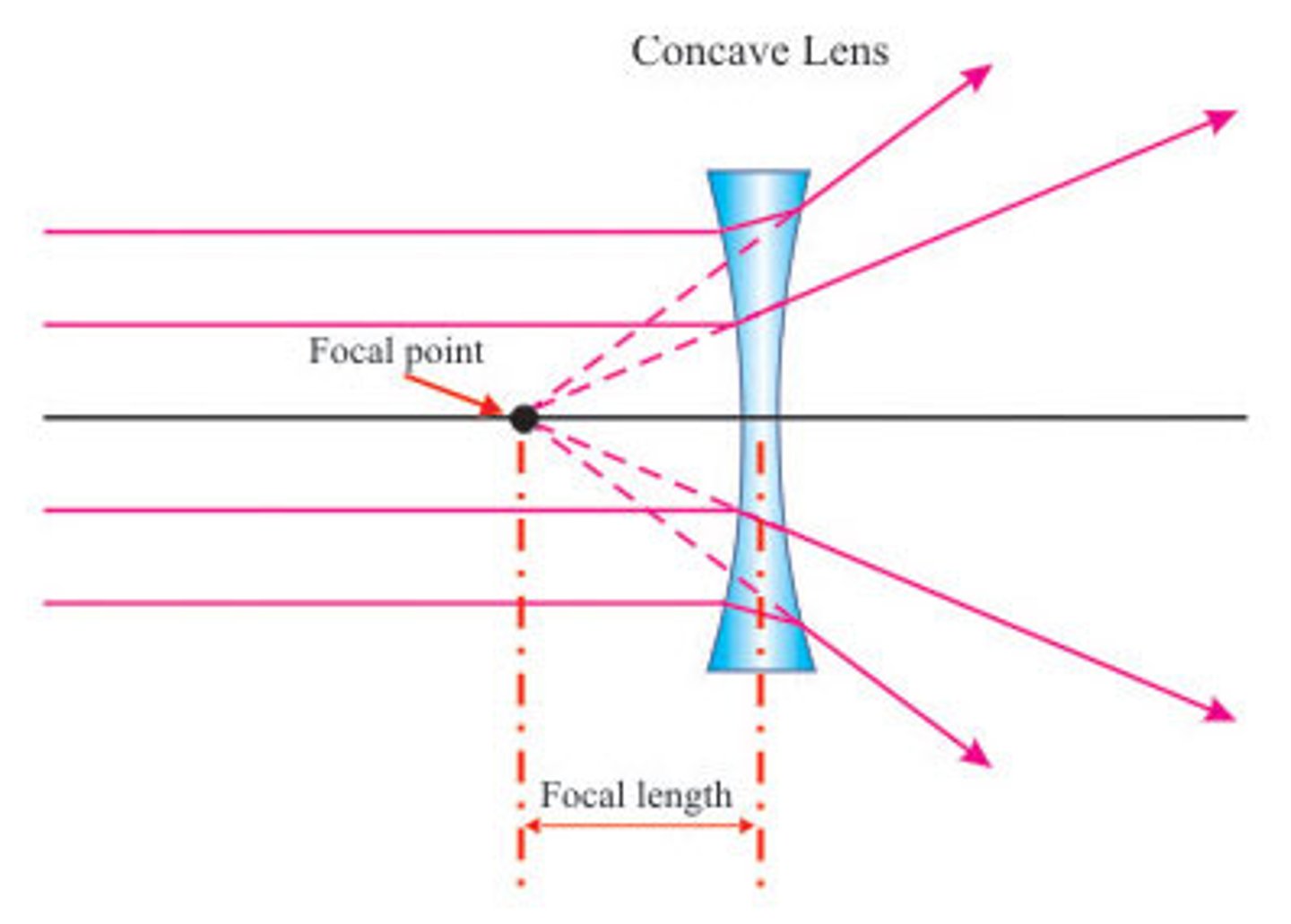
Image formation on a curved surface

Lenses are curved surfaces on which light rays refract.

If light rays meet, an image will form.

The angle of refraction depends on the index of refraction of the medium.

A diagram of this should begin with drawing a normal ray which passes through the center of curvature, and travels perpendicular to the surface- no refraction!

The incident angle of other incoming rays needs to be measured with respect to the normal.

Principal light rays

In geometric optics, image formation is made by emerging of 3 principal light rays (parallel,focal and center). In case of converging lens it looks like this:

Lens combinations

Lenses are combined in a compound microscope to form a system of two lenses: objective and eye-piece lenses.

Image magnification can be manipulated by adjusting the distances between the lens and specimen as well as the distance between the two lenses.

refractive power

the degree to which lenses are able to converge or diverge light.

formula: D=1/f (f=focal point)

lens equation

Reciprocal of the image distance plus the reciprocal of the object distance, gives the reciprocal of the focal point, which equals the refractive power.

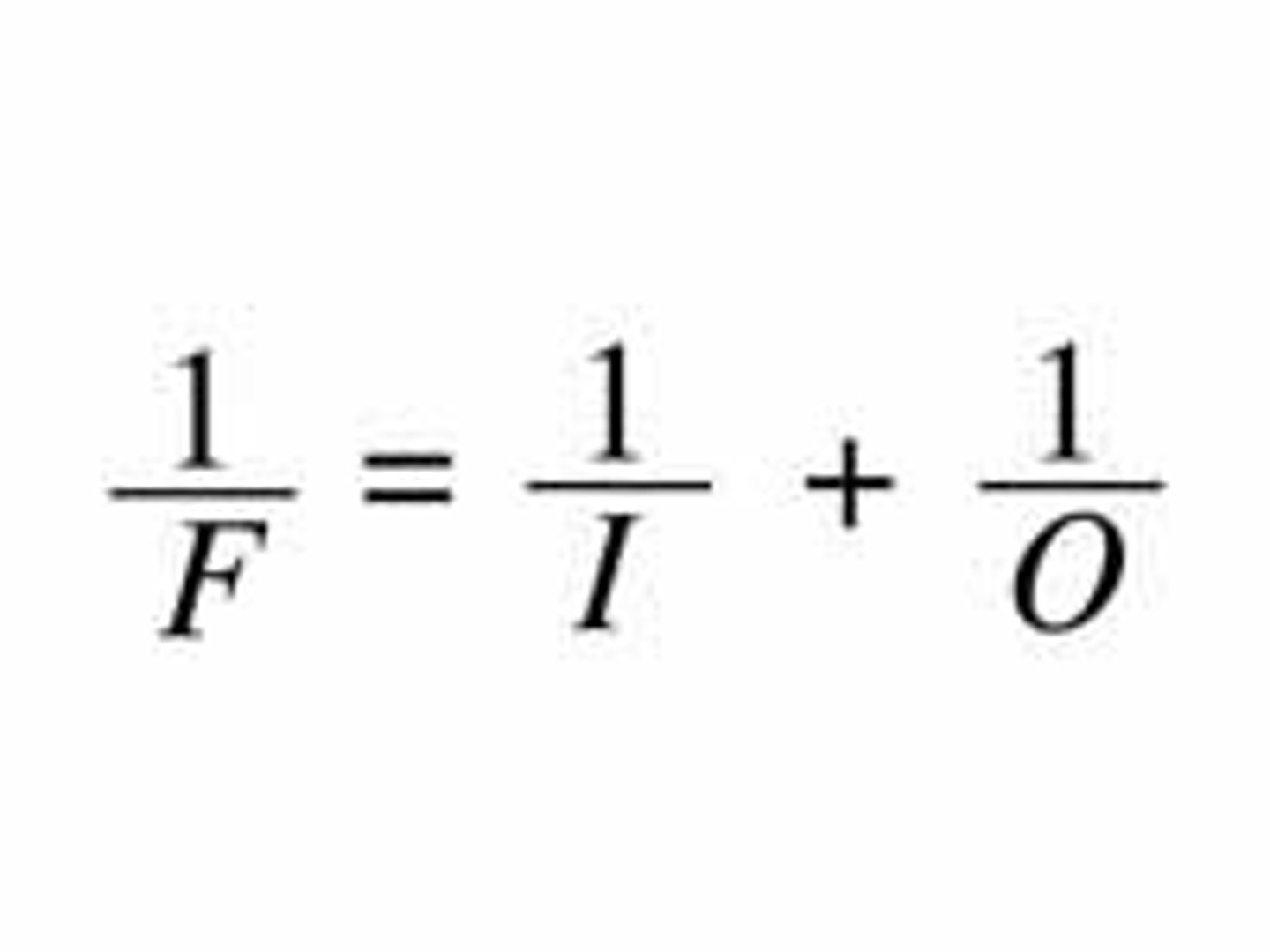
Image formation by the light microscope

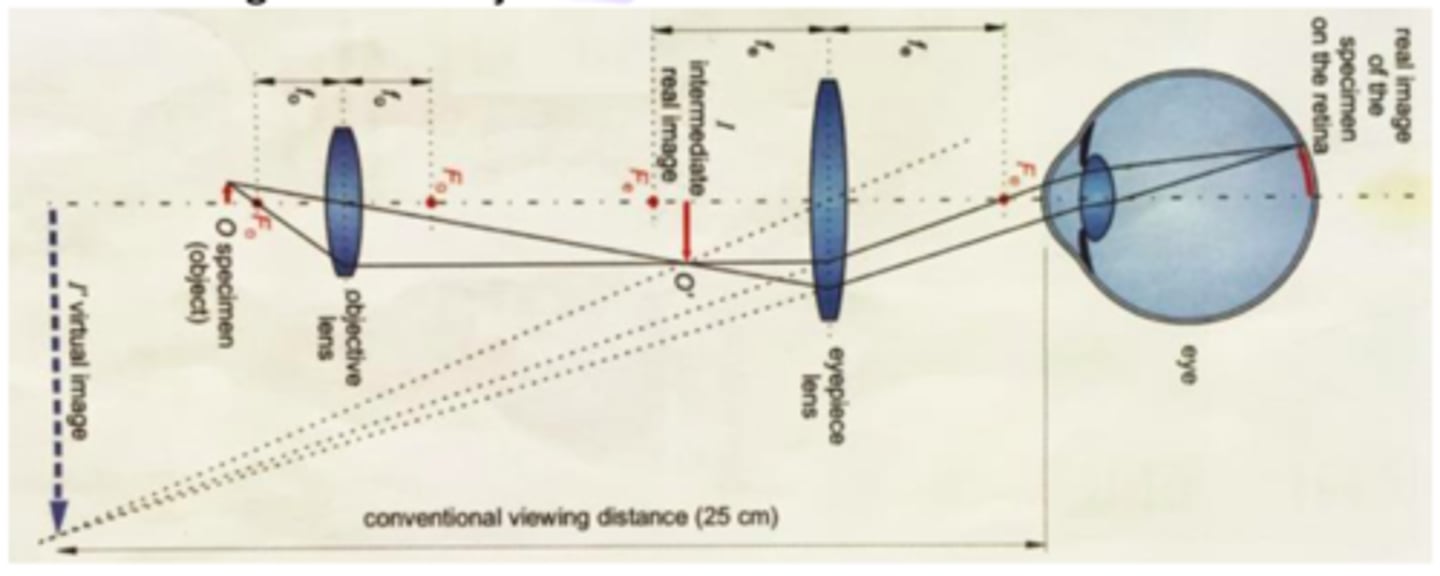
Concepts of magnification and angular magnification.

magnification is the ratio b/w image and object sizeangular magnification define as the ration b/w tan beta(angle of the image)e and tan alpha (the angle of the object)a.in case that the image is form on the near point [M(angle)=(nearpoin /focal length)+1] (near point=0.25meter) b. in case the image form at the infinity: M(angle)=nearpoint/focal length

Rules of image formation.

Depending on where the object is placed with respect to the focal point and double focal point, will determine the type of image that will be formed.

● Object is beyond 2F: image is real, inverted and diminished.

● Object is at the double focal point: image is real, inverted and the same size.

● object is between 2F and F: image is real, inverted and magnified.

● Object is at F: image is (virtual, upright and magnified at infinity) - Magnifying glass

● Object is closer than F: image is virtual, upright and magnified.

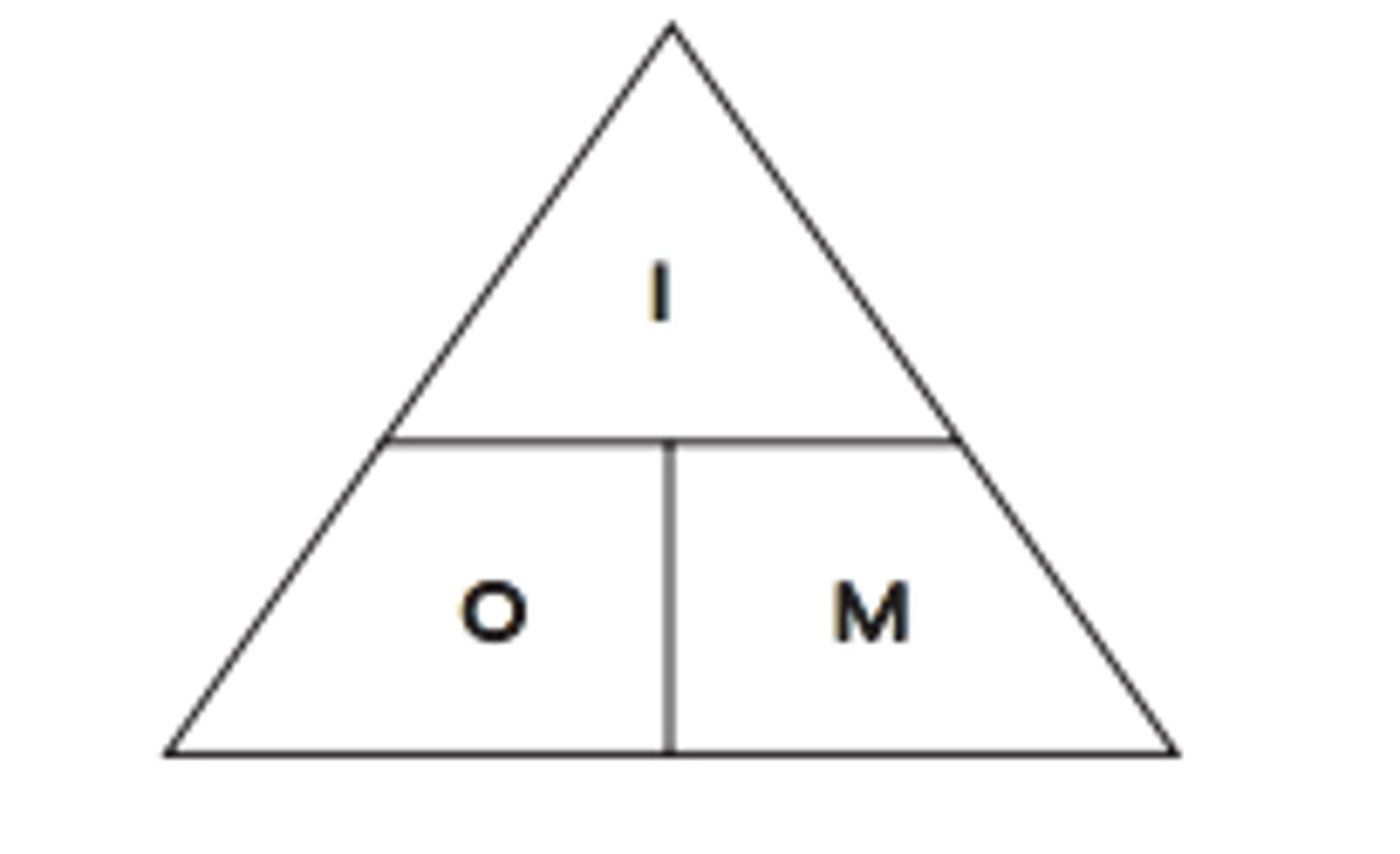
Magnification in the light microscope.

The product of the magnifications of the objective lense and the eyepiece lense: M=I/Ox(I'/O')=MoxMe

Oscillations.

Phenomenon in which quantity varies as a function of time around an equilibrium value

Diffraction on an optical grating.

A structure with periodic optical properties. Its characteristic feature is the grating period (d) with a size on the order of the wavelength.

Polarization of light.

A process which unpolarised light (light whose electric field vectors propagate in more than 1 plane, which contains the direction of propagation) become polarized light (light whose electric field vectors propagate only in 1 plane, which contains the direction of propagation) by an optical filter (polarizer)

Types of waves.

Sound waves (longitudinal or transverse) - require a medium

Electromagnetic waves (transverse waves) - do not require a medium

Matter wave (matter can act as a wave; electrons can have wavelike interference)

Limit of resolution of the light microscope.

The smallest noticeable distance btw 2 points.

Abbe's formula: omega = 0,61x(wavelength/nxsinomega)

color which the sum of them is the white light

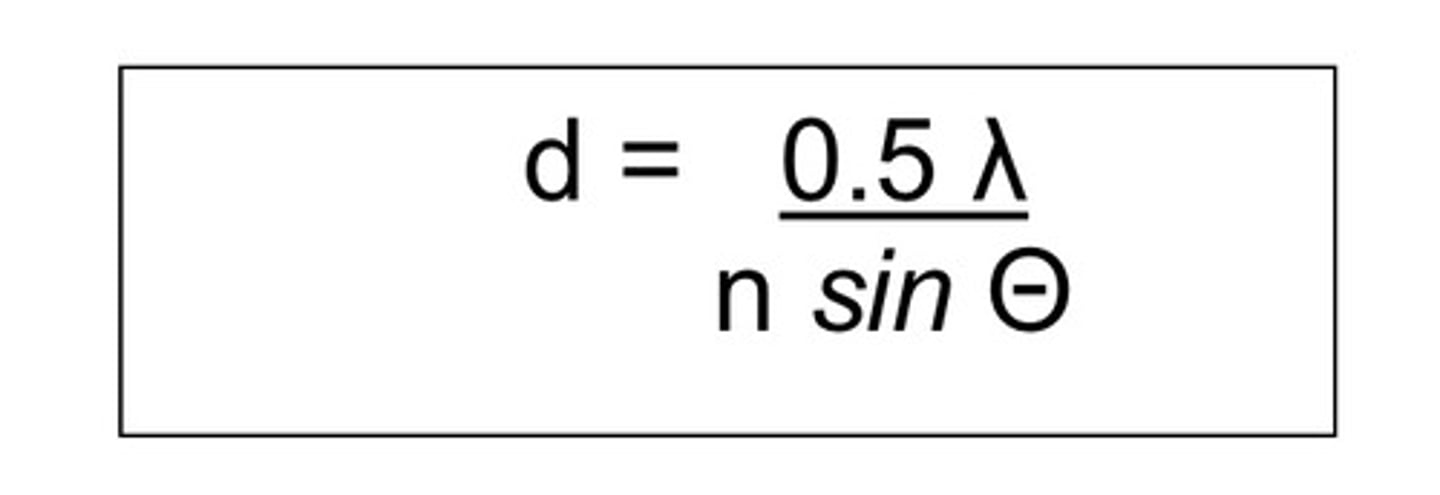
phase contrast microscope

Turns phase differences (to which the eye is not sensitive) and converts them into amplitude differences which translate to intensity differences

I = A2 (which the eye is sensitive to).

Useful for studying living cells, with no staining

Huygens-Fresnel principle.

Every wave propagates so that each point of its primary wavefront serve as a source of secondary wavelets (of small amplitudes) that advance with the same speed and frequency as the primary wave.

Polarization microscope.

A technique that makes birefringent details of a specimen visible.

Examples of birefringent materials include: cell membranes, striated muscle and myelin sheath of neurons.

The microscope is equipped with a polarizer which illuminates the specimen with linearly polarized light.

On the other side of the specimen, another polarizer is used: "an analyzer", at 90 degrees from the polarizer. At this angle the view is dark.

Light which was rotated by birefringent parts of the specimen passes, so that only these details are visible.

a Wave interference.

Combination of at least 2 EM waves which encounter and result in:

a. constructive interference: same phase (crest meet crest) or

b. destructive interference: opposite phase (crest meet trough)

wave diffraction

When light passes through a slit which is near the size of the wavelength, it will spread around the slit.

Ties us back to the Huygens-Fresnel principle, which explains diffraction.

It results in a diffraction pattern.

Interpretation of the color of light.

The different colours are the perception of our eyes for different frequency (different of EM radiations in the visible range)

*complementary colour: object absorbs color and transmits other colour which the sum of them is the white light

Wave nature of light.

Diffraction, interference, polarization are phenomena which

prove the wave nature of light.

Dual nature of light.

light can behave in some cases as a wave (e.g. interference) and in other cases as a matter (e.g. photoelectric effect)its energy packed in quanta that depends on the frequency.

Matter waves.

The concept that matter can exhibit wavelike properties. Hypothesis by De-Broglie, who introducedthe wavelength for matter:

wavelength = h/p = h/mv

Where it equals the ratio of planck's

constant and the momentum of the particle.Example: Davisson-Germer experiment which proved that electrons, which were scattered, formed diffraction patterns.

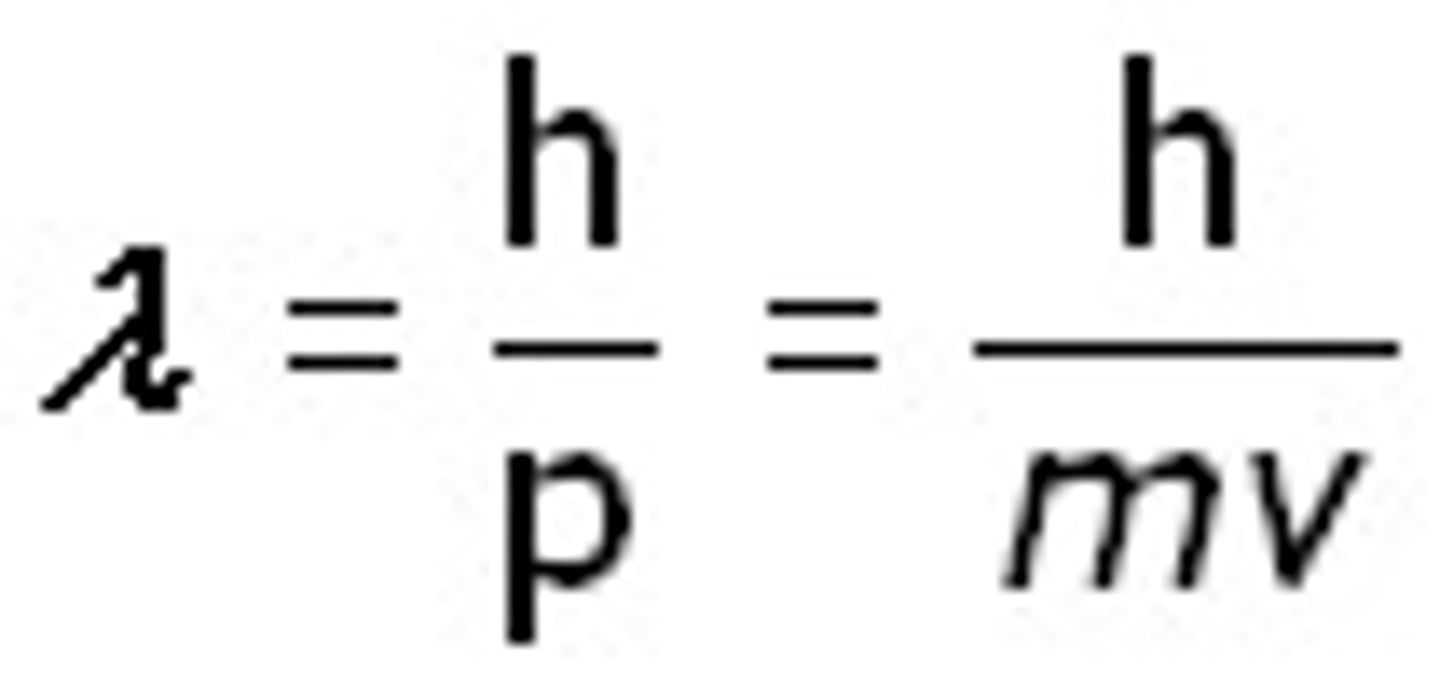
electromagnetic spectrum

All of the frequencies or wavelengths of electromagnetic radiation

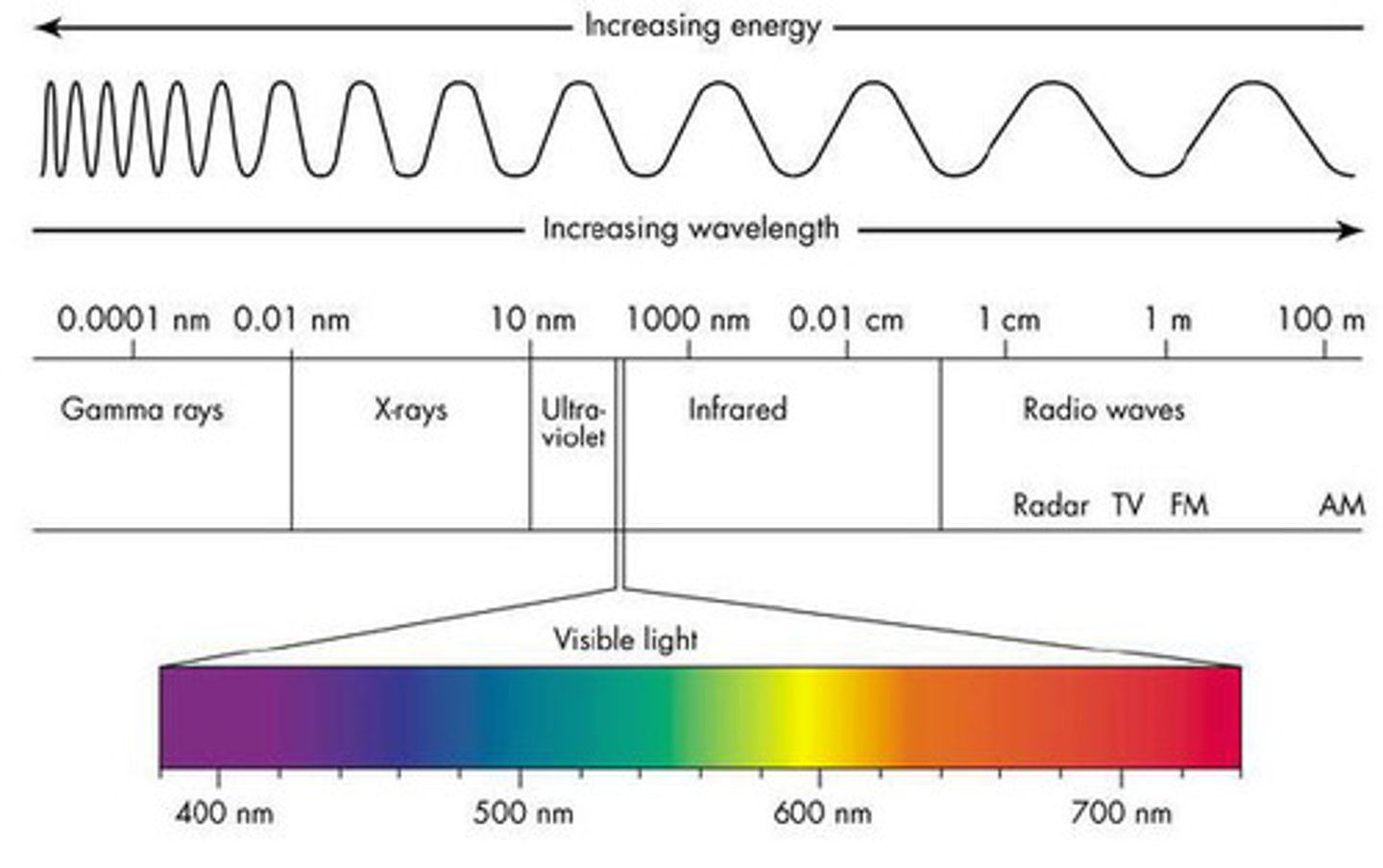
The photoelectric effect.

When a photon of energy E = h * f delivers enough energy to an electron, causing it to leave the atom. Experiments by Einstein proved this because not all types of light will result in the ejection of an electron, only lights of sufficient energy (UV for example). This proved the quantized nature of light =photon and thus the particle nature of light (and got him the nobel prize)

The electron microscope.​

Due to the small wavelength of the electron comparing to a photon the resolving power of electron based microscope allow us much higher resolution (abbe's formula and the de broglie relation )2 main types of electronic microscope : Transmitted electrons ( electron going through the sample and create the image on a screen) and Scanning EM (the scattered electrons create the image)the basic principles are: electron gun (tungsten filament which wired to an electric circuit, heats up and electrons shoot out due to their thermal thei thermal E), high voltage for the acceleration of the electrons(30kV-300kV), condenser electromagnetic lenses.

Photon energy, the eV scale.

Photon energy is calculated as the product of planck's constant and the frequency.

E = h f or E = h c/λ

The energy is the formula is given in joules, but is often described using electron volt.Electron volt: the amount of kinetic energy in an electron that is accelerated in an electric field of one volt.

1eV = 1.6 * 10^−19 Joule

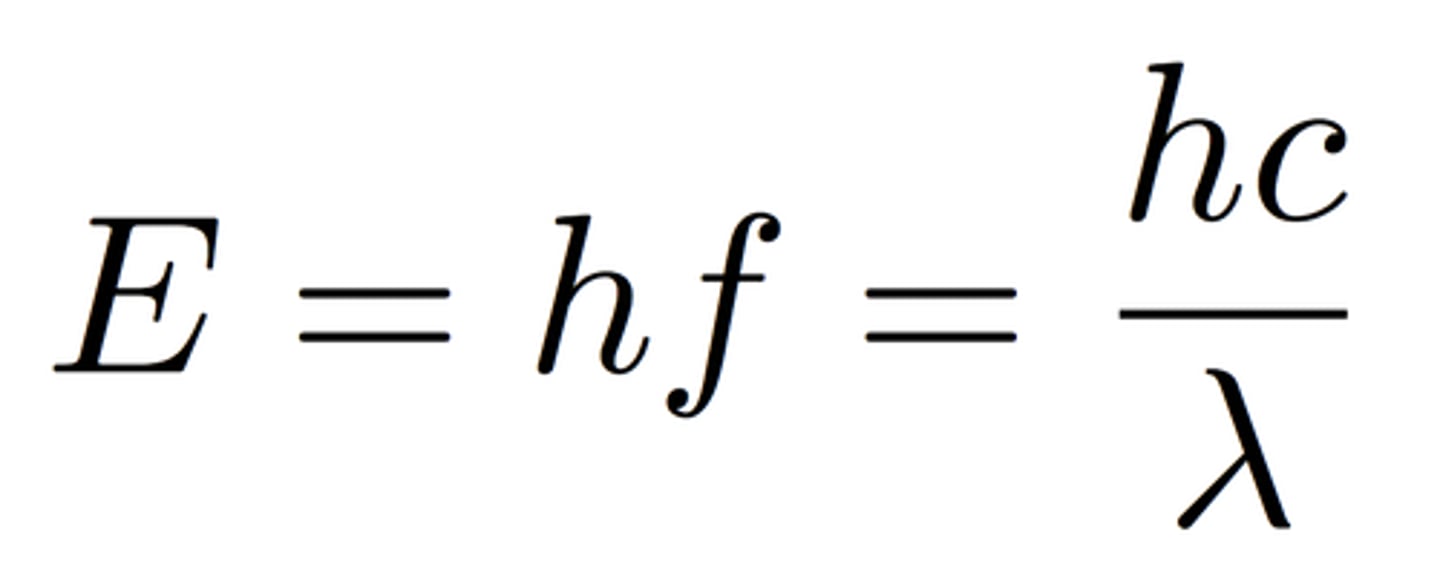
Interpretation of momentum of light: optical tweezers.

Formula for photon momentum:

ρ=h/λ

Optical tweezers ​utilize the momentum of the laser beam to control little refractive microshpere structures which can be bound to a biological molecule and be controlled by moving the laser.

Models of the atom (Dalton, Thomson).

Models of the atom:​

Democritus: "Atomos" (​uncuttable) atoms are the smallest article, and they have different shapes.

Dalton:​ showed that matter was made of indivisible particles (atoms) which can not be broken down further.

Thomson:​ discovered that atoms had electrons which were stuck throughout the positively charged substance (plum pudding)

Rutherford:​ showed that all the positive charge was in the middle (nuclear model: atom has a nucleus)

Bohr: ​the concept that electrons orbit around the nucleus (simplified concept used in chemistry for simplicity)

Schrödinger:​ electrons don't move in concentric circles, rather orbitals can have different shapes which are not necessarily circular (quantum mechanical atoms).

Rutherford and Chadwick: ​discovered protons and neutrons. (further quantum mechanical atoms)

Wave nature of the electron.​ Davisson Germer experiment

Electrons behave like waves in certain situations like being diffracted.

We can calculate the wavelength of electron the formula for de Broglie:

wavelength=h/p, when p(momentum)= mass*velocity

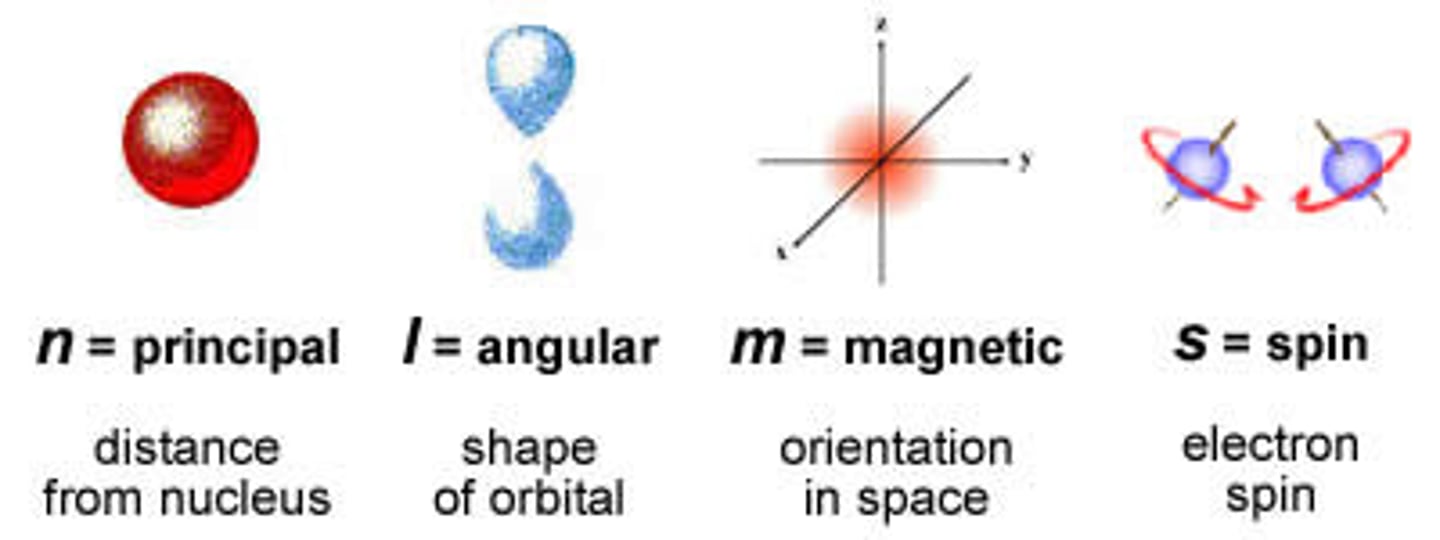
The bound electron, quantum numbers.

Principal quantum no (n): 1, 2, 3, 4..

Angular momentum quantum no (l): n-1

Magnetic quantum no (m1): -l...+l

Spin quantum no (ms): +1/2, -1/2

Bohr's atomic model.

Electrons in an atom can only occupy certain distinct orbits around the nucleus.

The electrons in their orbits won't radiate unless they will be excited and jump to an higher orbit.

We can calculate the frequency of a radiated electron by calculating the difference of energy btw the 2 orbitals using this formula: hf=Em-Ei

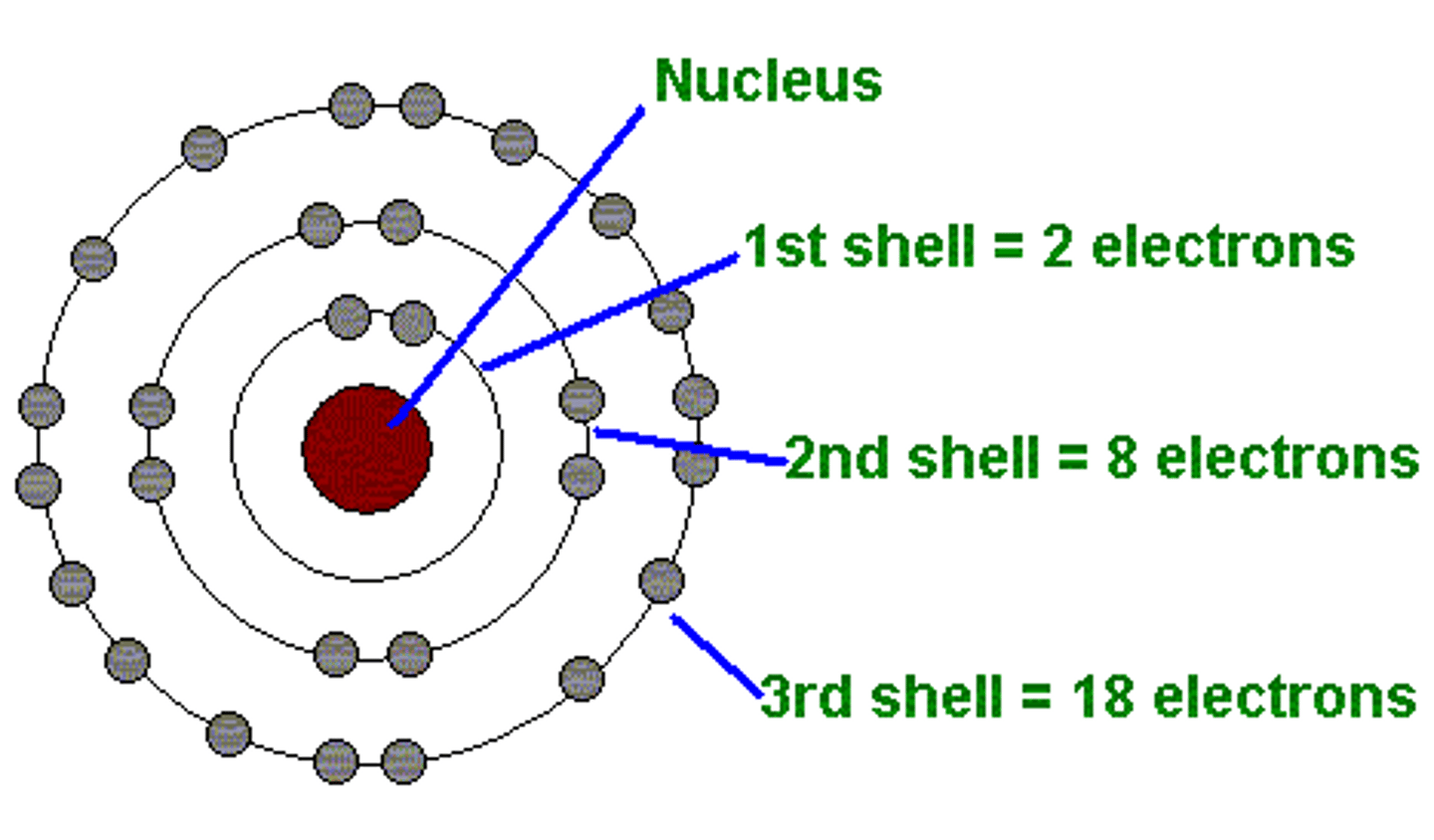
Heisenberg's uncertainty principle.

One cannot know all the parameters describing a particle at a given time.

For instance, when momentum is calculated, there is more uncertainty about its location and vice versa.

This is due to the wave nature of particles.

​For example:​ when waves are compressed enough into one space, to gain information on it's exact location, it will not be possible to know the exact momentum of that wave.

In the case of sound, the more we know about its location in space, the less accurately its frequency is determined.

Physical foundations of the periodic table.

a. Numbered according to the numbers of protons

b. Size: increases from right to left in the period and from up to down in the group

c. In every group the number of valence electrons is the same

d. Ionization energy: increases in the group from bottom to the top and in the period from left to right (oppositely to the atom size orientation)

e. Electron configuration: s,p,d,f blocks (d=-1 f=-2)

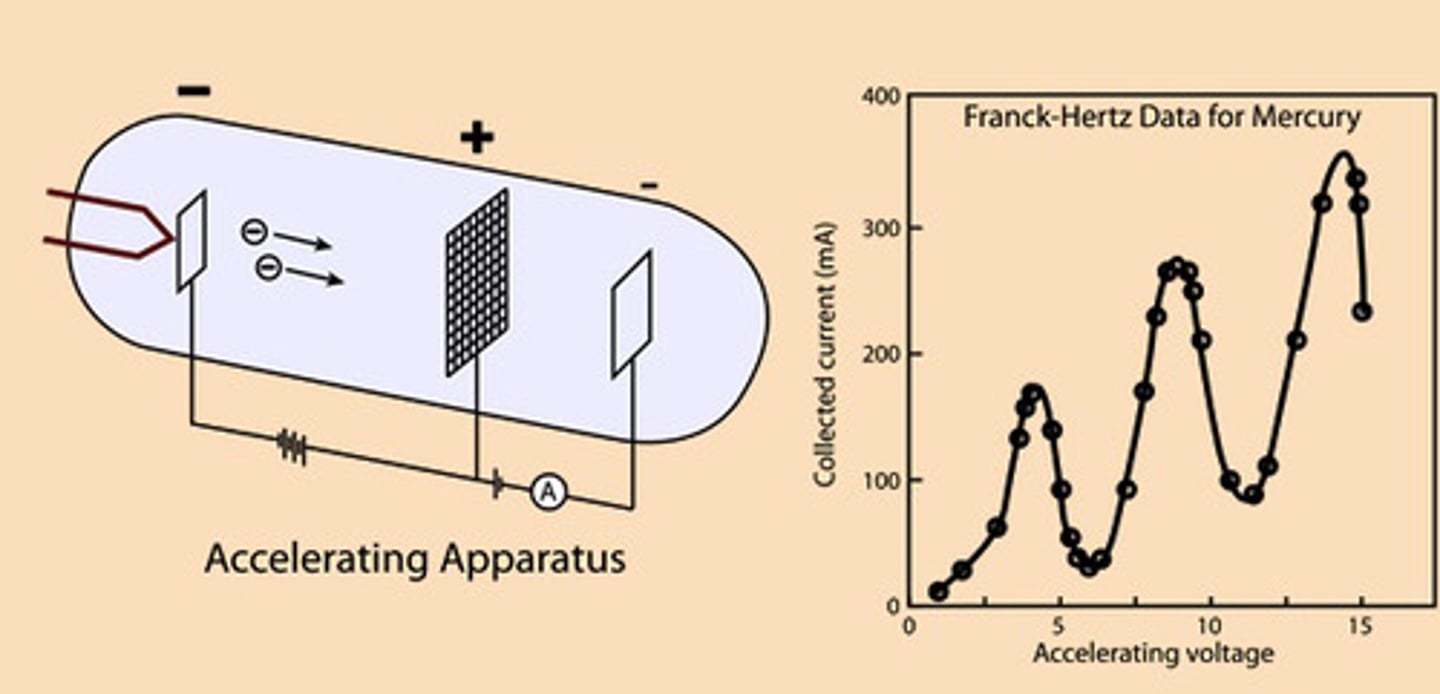
Franck-Hertz experiment.

The purpose of the experiment was to prove Bohr's atomic model, which states that electrons exist in quantized states within the atom.

In the experiment, using a tube filled with Hg, an electron emitting cathode, a grid and an anode, it was proved that in order to interact with the Hg atoms, a specific discrete amount of energy had to be given to the electrons, by means of voltage.

By measuring the current at the end of the tube, it was possible to measure how much of this energy was imparted on the atoms, and how much was left over, and thus the quanta of that particular atom.

Potential energy of interatomic interactions.

Atoms within a molecule are organized in more or less fixed positions in which the molecule stores the least potential energy, thus is in its most stable.

Sccording to this formula : E pot.=Eattraction+Erepulsion

and this graph: (figure I.19 in textbook)

Electronegativity

A measure of the strength with which an atom will hold on to its electrons and can ionize other atoms. $

Atoms of small size with a high atomic number are more electronegative

(larger nucleus = more positive charges, yet small in size means electrons are closer to nucleus and that they don't produce much shielding for valence electrons, from the nucleus)

Most electronegative atom is Fluorine.

In a bond, atoms of higher electronegativity will pull electrons towards them, causing polarity in a molecule.

Scanning probe microscopy.

Principle: a method which can form an image of an atomic size object by detecting various interactions depending on the design probe.

e.g.: AFM which measures the van der waal's force btw. the probe and the sample

(the probe attracts to the sample until a certain distance, and after a certain value the force of repulsion takes place. The deflection of the cantilever is held constant by lifting or lowering the cantilever.)

Composed of: a probe which is connected to cantilever and a laser beam that point on the probe and reflect into detector (measures the change in the position of the probe)

2 modes: contact, oscillating

Primary and secondary bonds.

Primary bonds:​ include covalent (non metal-non metal), ionic (metal-non-metal) and metallic (metal-metal) bonds in which electrons are shared between atoms, in order to form a more stable electron configuration. ​Secondary bonds:​ are weaker because there is no electron sharing, rather bonding occurs due to instantaneous dipoles between two atoms.

Van-der waals and hydrogen bonds are secondary bonds

Resolving power of the atomic force microscope.​

Atomic scale (sensitive to the van der waal's attraction) Resolution is in the order of fractions of a nanometer, which allows the study of strength and length of chemical bonds and the detail of molecular structure.

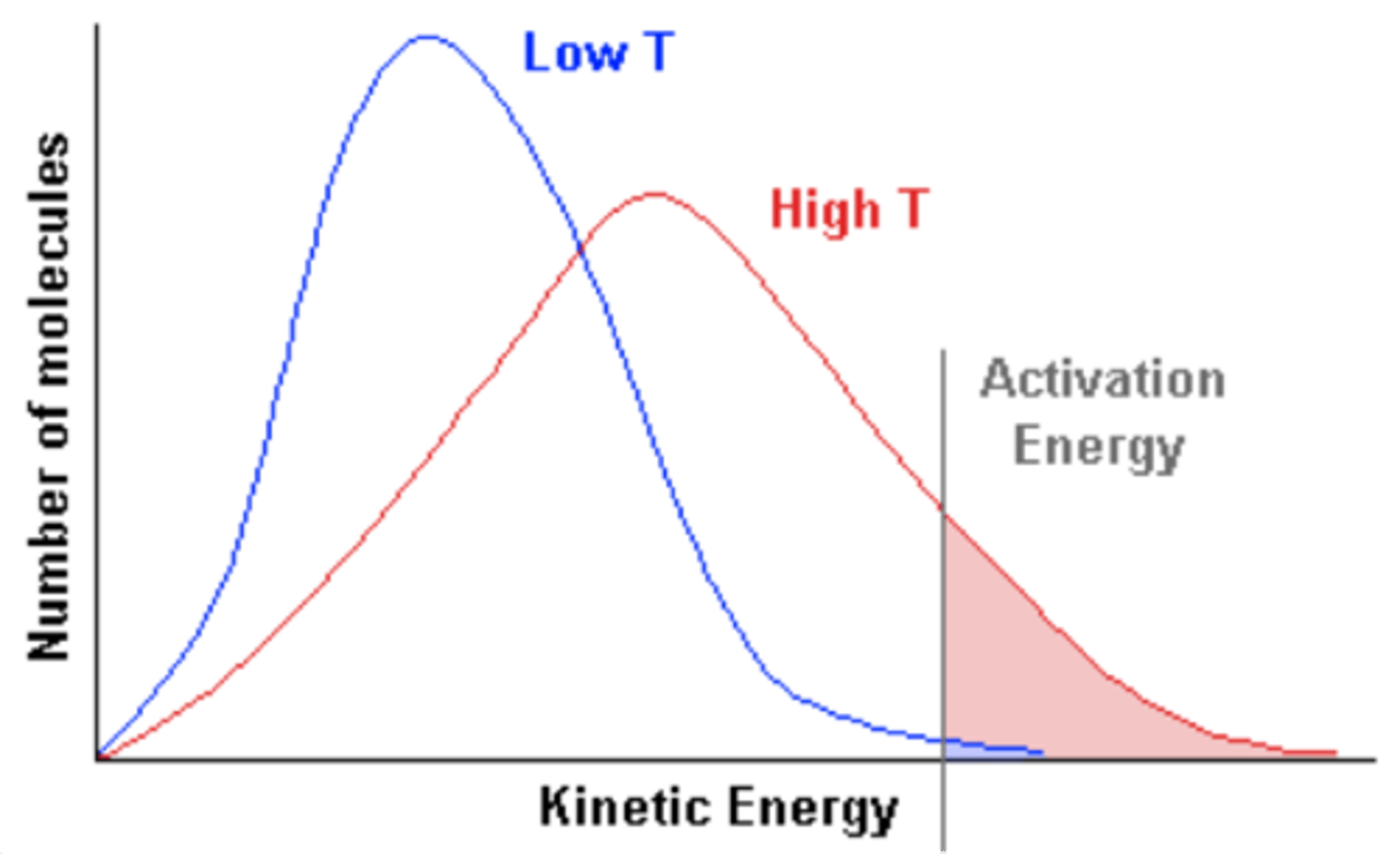
Boltzmann distribution.

A universal organizing principle, in which energy levels in a thermally equilibrated system are populated by an exponential function. At higher temperatures, higher energy levels are more populated.

P(h)/P(0)=e^(-mgh/kT)

Applications of the Boltzmann-distribution I. : Nernst equation.

Epot=qU(chargevoltage)

The distribution of charge particle at point A and B can be calculated by this formula: nA/nB=e^(-qU/kT)

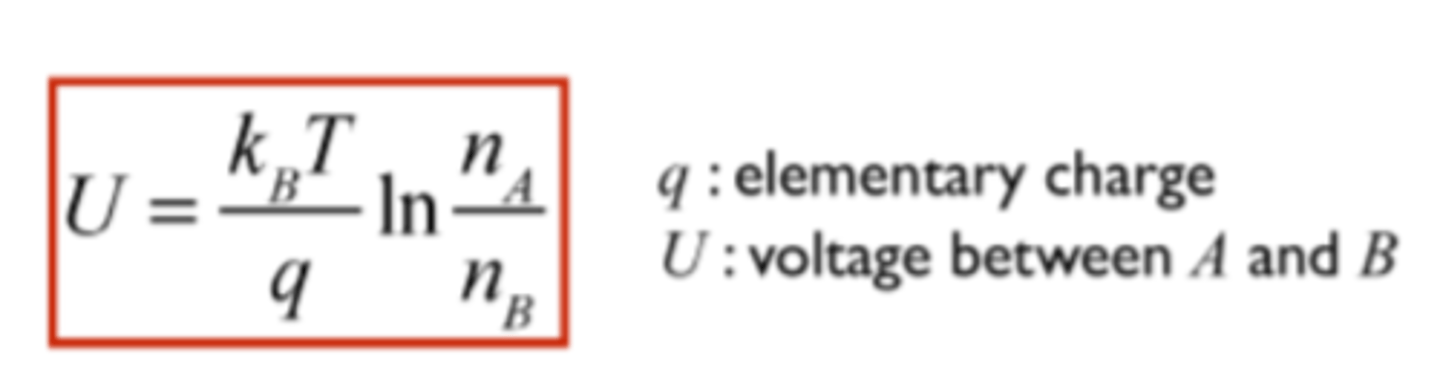
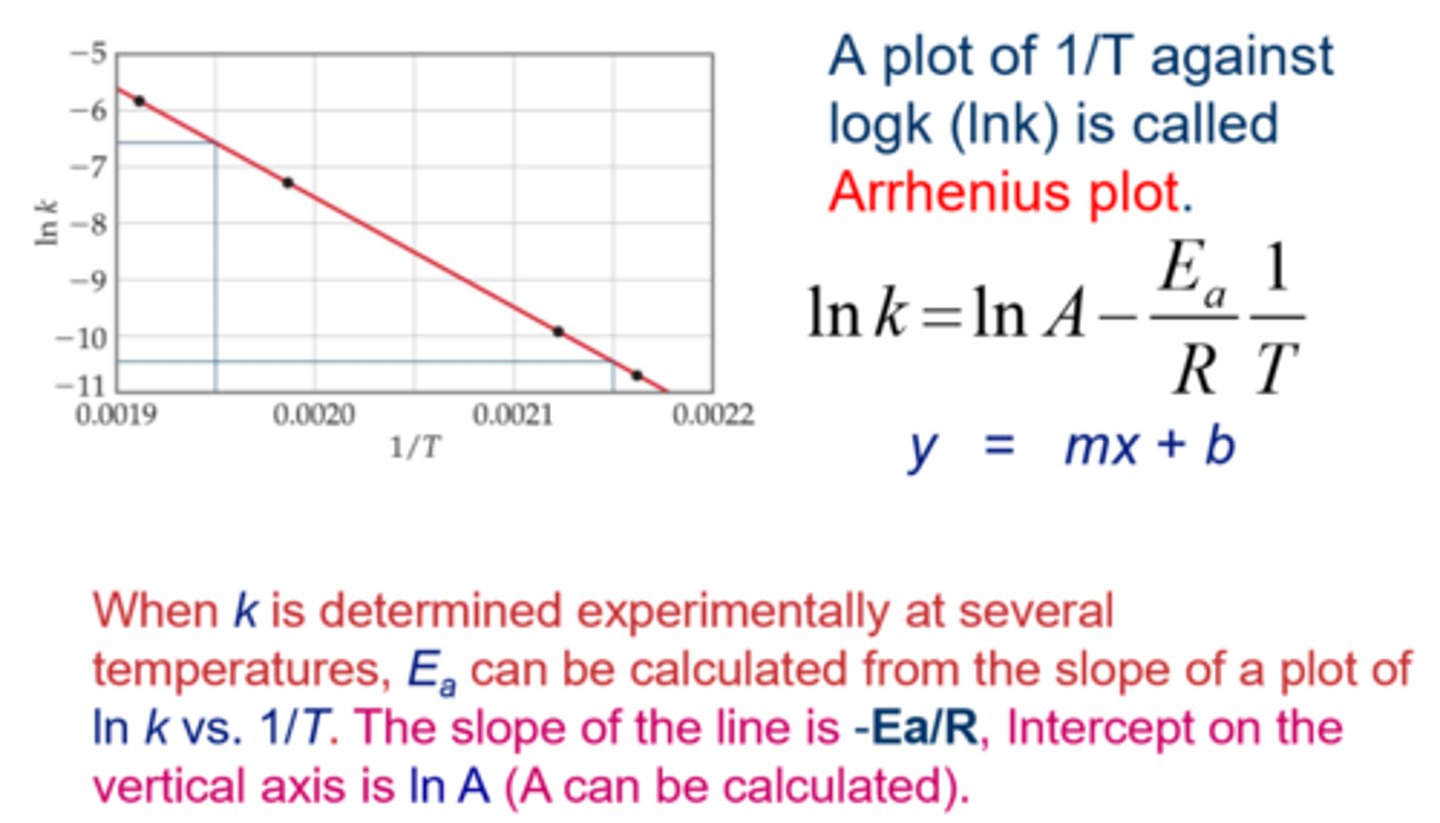
Applications of the Boltzmann-distribution II.: equilibrium and rate of chemical reactions. (The Arrhenius plot).

In chemical reactions, atoms must transition from one energy state A in which its energy is εa to B state in which its energy is εb.

In an equilibrium, the distribution between those states is calculated: nA/nB =e^-(εA-εB/kT).

The ratio na /nb = K (equilibrium constant)

The Arrhenius plot illustrates a logarithmic relationship between the K and the 1/T.

The slope of the graph gives the energy distribution between the two states.

Applications of the Boltzmann-distributionIII.: barometric formula.

In thermal equilibrium, we can measure the decrease in atmospheric density vs altitude by this formula: (density of gas is concentration per volume, so we practically measured the distribution of concentration)

rho(h)/rho(0) = e^-mgh/kT

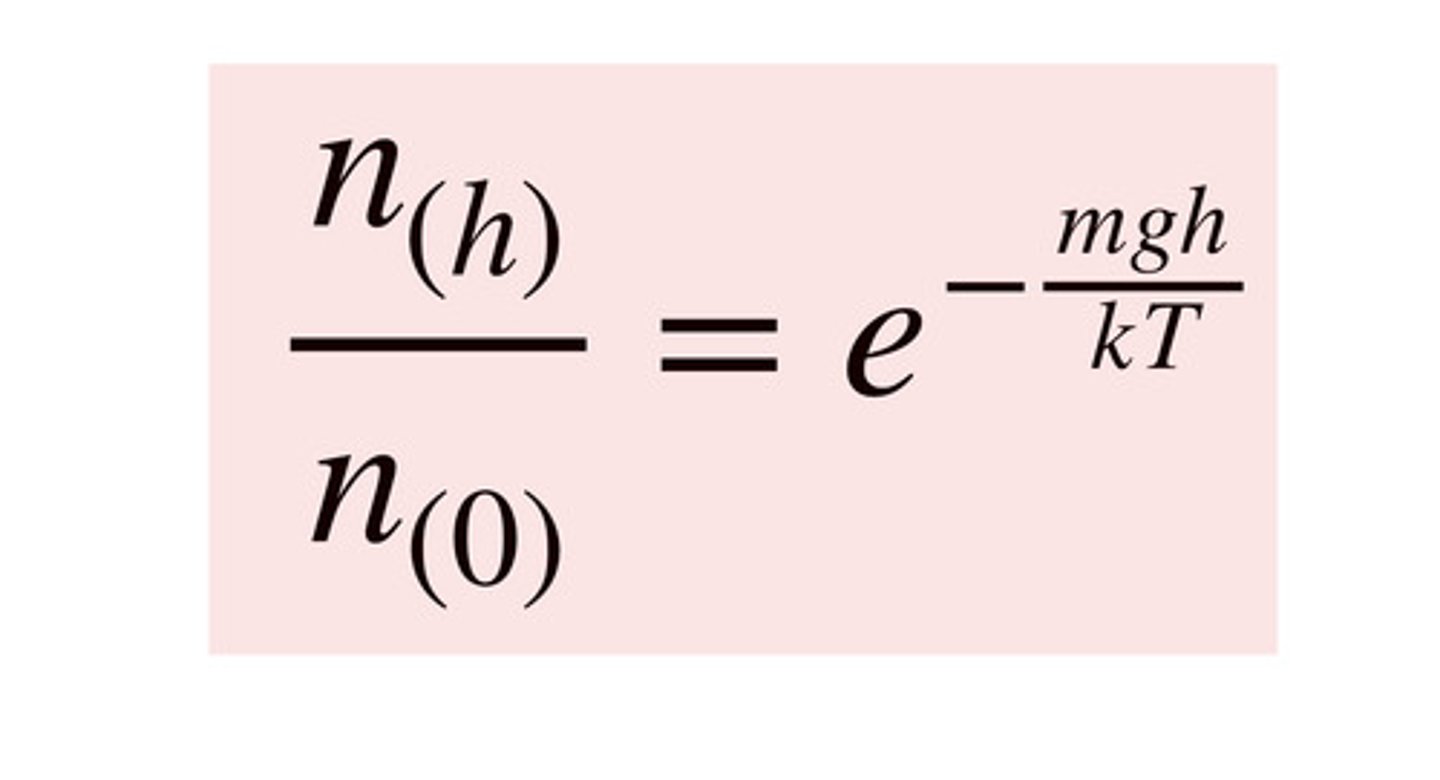
Applications of the Boltzmann-distribution IV. electric conductivity of semiconductors.

Electric conductivity of semiconductors (a type of crystal) depends on the number of electrons which are able to transition from the valence band through the "gap" to the conduction band.

This number increases with T (it is the opposite in conductors).

Using the Boltzmann distribution, we are able to calculate the fractions of electrons that are able to cross the "gap"/"forbidden band" = Δε : (n/n0)=e^-(Δε/kT)

Macrostate and microstate in thermodynamics.

Microstate:​ examination of the molecular state of the system and instant state (location of particles, velocity of particles, momentum)

Macrostate: e​xamine the system as a whole (temp. pressure) in thermal equilibrium the macrostates stay constant while the microstate always changes!

Kinetic gas theory.

5 main assumption which explain the behaviour of gas (ideal):

1) Particles are very small compared to the total volume

2) Constant random motion

3) Colliding of the particle one another is elastic

4) Particles exert pressure on walls when they are under higher psi/temp

Boltzmann's definition of entropy.

S = k * lnΩ

where S = the entropy (the extensive quantity of heat) and where the number of microstates which belong to a particular macrostate are.

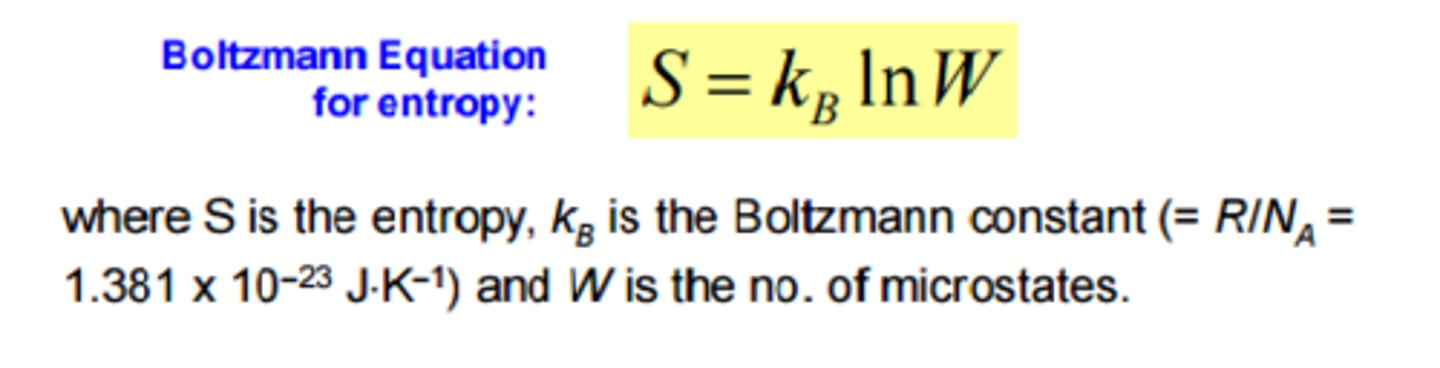
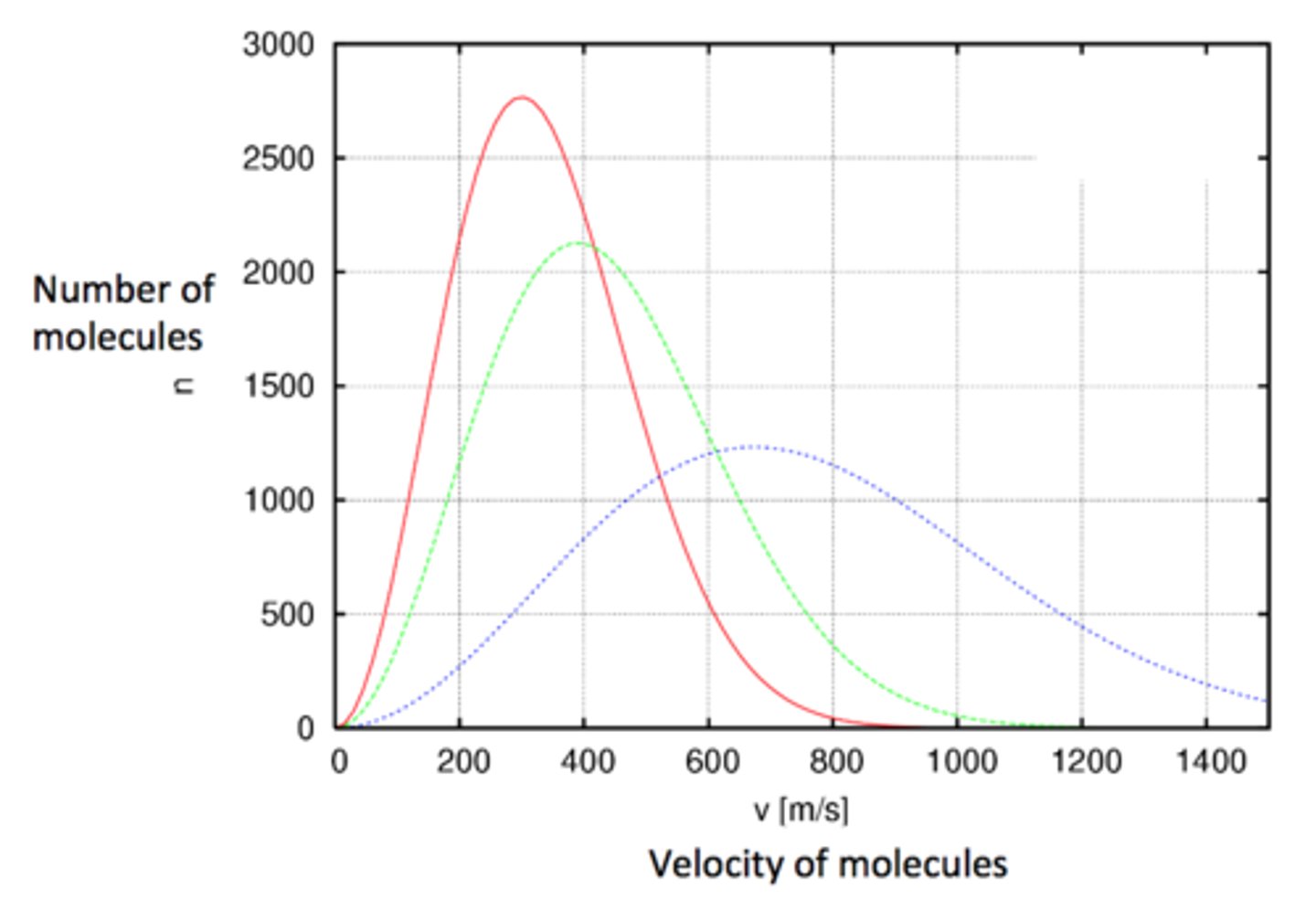
Maxwell-Boltzmann velocity distribution.

Upon increasing the temperature, the average of the absolute value of molecular speed increases.

The width of the distribution increases due to an increase in the interactions between the molecules.

(+ graph)

The Ideal gas.

Refers to non-realistic gas composed of molecules which follows the kinetic gas theory.

The parameters characterising the state of the gas are connected by this formula : PV=NkT

(temp. in kelvin)

The real gas.

Contrary to theoretical "ideal gas": Particles are not point-like, their volume is not negligible, consequently there is less volume available for motion.

Interactions between particles arise and pressure becomes reduced.

Additionally, behavior of real gases explains the possibility of condensation (transition from gas to solid)

State equation of real gases.

Using van der Waal's equation which adds to the formula of ideal gas, some factors occurred in real life e.g.: particles have volume, there is interaction btw. the molecules, and thus there are less molecules and energy which collide on the walls of the container and form pressure.

(constant a = correction for the intermolecular force, constant b = correction for the volume of particles).

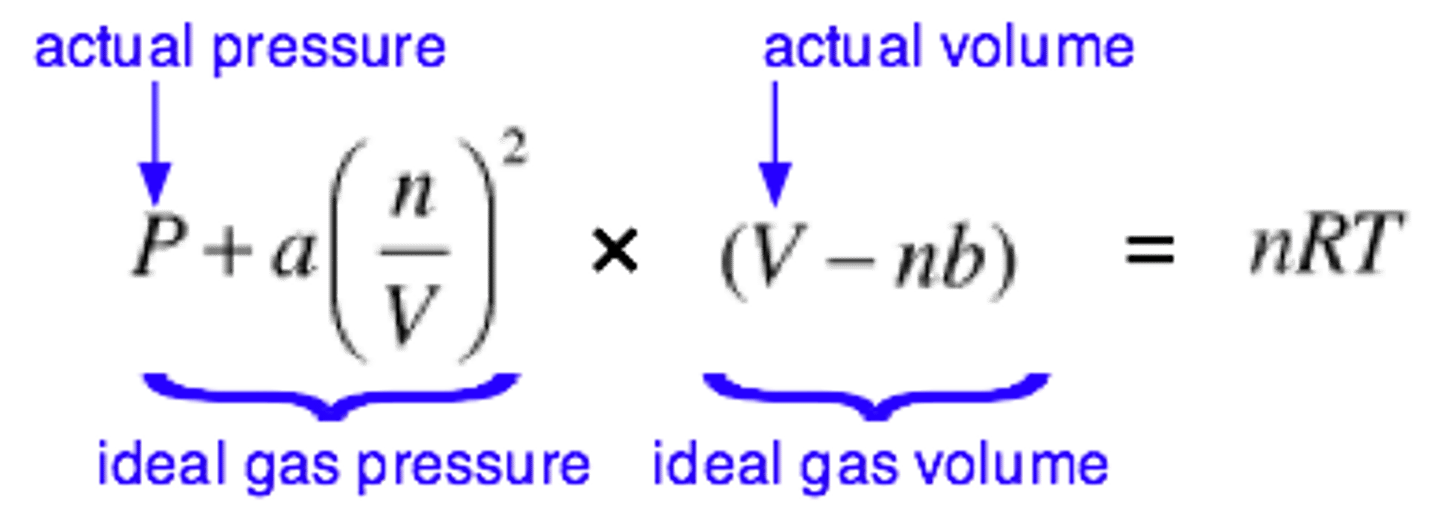
Pressure of ideal gases.

Assuming no interactions between particles, and negligible particle volume: pV=NkT or pV=nRT.

k= boltzmann constant

n=moles

N=number of particles

R= gas constant

The crystalline state (unit cell, crystal defects).

Solid which is arranged in a long range of periodic order and is composed of structural units which call the ''unit cell'', the latter making a bigger symmetrical structure called ''crystal lattice''.

As in gases, we have a classification of ideal and real crystals.

While ideal crystals have infinite periodic spatial sequences of identical structural elements, real crystals or microcrystalline keep their identical spatial sequence only in their microscopic scale and instead of being made of the same crystalline structure (same elements, same type of lattice) they appear in various sizes and orientations of building blocks.

Crystal defects:

a. point defects = occur on a single lattice point (types: empty space, doping, an extra atom btw. the lattice point)

b. line defects = rows of atoms are arranged inconsistently

c. surface defects = boundaries which separate the crystal into regions with different orientations.

defects can cause fracture in the crystal.

Optical properties of crystalline materials.

They are anisotropic, which means that their physical properties are dependent on the direction of the measurement related to the orientation of the atoms in the crystal.

Due to this, light will propagate with different velocities in different directions.

Thermotropic liquid crystals.

Liquid crystal: s​ubstance which possesses properties of both liquid and crystalline solid.

2 types of order can be defined liquid crystal:

a. Transitional order- the center mass point of the molecule form plane

b. orientational order- the axes of the molecule alin almost parallel with one another

thermotropic- the order of the structure depends of temperature

Application: contact tomography: the changing colors of choloresteric film on the patient's body can indicate inflammation area (higher temp. than normal=different color than normal)

Lyotropic liquid crystals.

Their order is affected by the concentration of their components (they change order depending on how many of them there are).

Their components are amphiphilic molecules which form ordered structures in the presence of a solvent.

Phospholipids, with their polar and nonpolar ends, form a membrane or micelles depending on their concentration.

Energy levels of electrical insulators.

Non-metals. In band theory, insulators are said to have a valence band and a conduction band, however the gap between them, the "forbidden band" where electrons cannot exist, is "too wide",

Δε > 3 eV, meaning that electrons are not able to cross it to get to the conduction band.

Therefore, it does not conduct electricity.

The function of the semiconductor diode.

It acts as a one way valve for electricity.

It is composed of n-type and p-type semiconductors. These are made by doping a semiconductor to achieve either free electrons (n-type) or holes (p-type). ​

​The chemistry behind ​the diode requires for p-type doping to be a chemical with lower number of valence electrons than in the semiconductor.

This will leave a vacancy which can be occupied by an electron (Al doping of Si).

For n-type, an element with more valence electrons than the semiconductor is used (P doping of Si).

Energy levels of electrical conductors.

Conduction band and valence band with no forbidden band in between. (note, heating of a conductor results in lower conductivity)

The liquid state.

● Lacks the spatial order of a solid (short-range order).

● Isotropic; have no directional dependance (unlike crystals)

● Take the shape of the container

● Not compressible (generally)

Electro- and thermo optical phenomena in liquid crystals.

Electro: nematic liquid crystal (characterized only by orientation order)

When they have electric dipole moment, the orientation of the molecule can be controlled by electric field.

The change in the orientation manipulates the optical transmission of the layer, which we can utilize to manufacture displays from that material.

Thermo:​ choleric liquid crystal (twisted nematic) changes its orientation as dependence of temperature (change the inclination​o​f its helix shape), thus the colour of the layer will change with different temperature (by destructive interference of one wavelength the crystal will transmit its complementary color).

One of those applications is the ''contact thermography'', which provides information about e.g. regional inflammation by the increased temp. in that region which means that the crystal will transmit different colors.

Energy levels of intrinsic semiconductors.

According to band theory, there is a valence band and a conduction band.

In a semiconductor, the gap between them is large enough that electrons do not pass freely.

However, the gap is not too large (Δε = 1eV ), therefore upon excitation, electrons can cross into the conduction band and electricity will be conducted.

Types of doped semiconductors.

1.p​ type (boron) (acceptor level) (holes) and

n type (phosphorous) (​donor level) (electrons)

Light scattering (Rayleigh and ​Mie).

Light scattering occurs when EM waves encounter particles in the air.

The light waves will cause a dipole moment, making electrons in the atoms vibrate (forced oscillation), which will cause them to emit light.

Rayleigh scattering​ depends on wavelength. (blue light is scattered more)

When particles are spaced far enough apart (spacing is larger than the wavelength), there is no interference, thus the intensity of incident light = intensity of scattered light.

We know that the dipole moment produced by the light is proportional to the angular frequency.

ω = 2πf (angular frequency)

Thus the higher the frequency the higher the scattering (blue light scatters much more → sky is blue)

Mie scattering,​ on the other hand, is not wavelength dependent, thus all wavelengths scatter equally (producing white light) when the size of the particle is on the order of the wavelength, this type of scattering occurs closer to the earth's surface. (H2O in clouds)

The Beer-Lambert law.

In a dilute solution, if the solvent does not absorb in the applied wavelength- absorption coefficient is proportional to concentration of solute thus:

(measuring concentration of solute by measuring the absorbance of light in a given wavelength)

Properties of the absorption spectrum.

Absorbance or transmittance as a function of wavelength.

Varies depending on the atom or molecule, as it depends on their electronic structure, thus can be used to identify an element.

Since absorption requires the excitation of an electron into the next energy level, it requires a photon of specific wavelength to make that transition: as a result some wavelengths will be absorbed completely, while others will be transmitted.

Turbidimetry and nephelometry.

Turbidimetry: Turbidimetry is involved with measuring the amount of transmitted light (and calculating the absorbed light) by particles in suspension to determine the concentration of the substance in question.

Amount of absorbed light, and therefore, concentration is dependent on;

a) number of particles, and

2) size of particles.

Nephelometry: at low intensity of scattered light, measures the intensity of scattered light. (linearly proportional to concentration)

Since the amount of scattered light is far greater than the transmitted light in a turbid suspension, nephelometry offers higher sensitivity than turbidimetry. • The amount of scattered light depends on the size and number of particles in suspension

how do we differentiate btw. light scattering and absorbance ?

Dynamic light scattering.

Is a method for analyzing solutions from which the hydrostatic diameter of a particle can be measured. Light is directed through a sample

→ scattering of the light occurs (relative to the position of the particles in the solution)

→ the intensity of the light is detected on the other side

→ intensity changes when the particles in the solution diffuse (brownian motion)

→ the change will occur faster or slower if the molecules are smaller, or larger respectively.

→ Information about the intensity is used to calculate the diffusion coefficient.

Next, Einstein-Stoke formula will allow us to calculate the r (size of the particle)

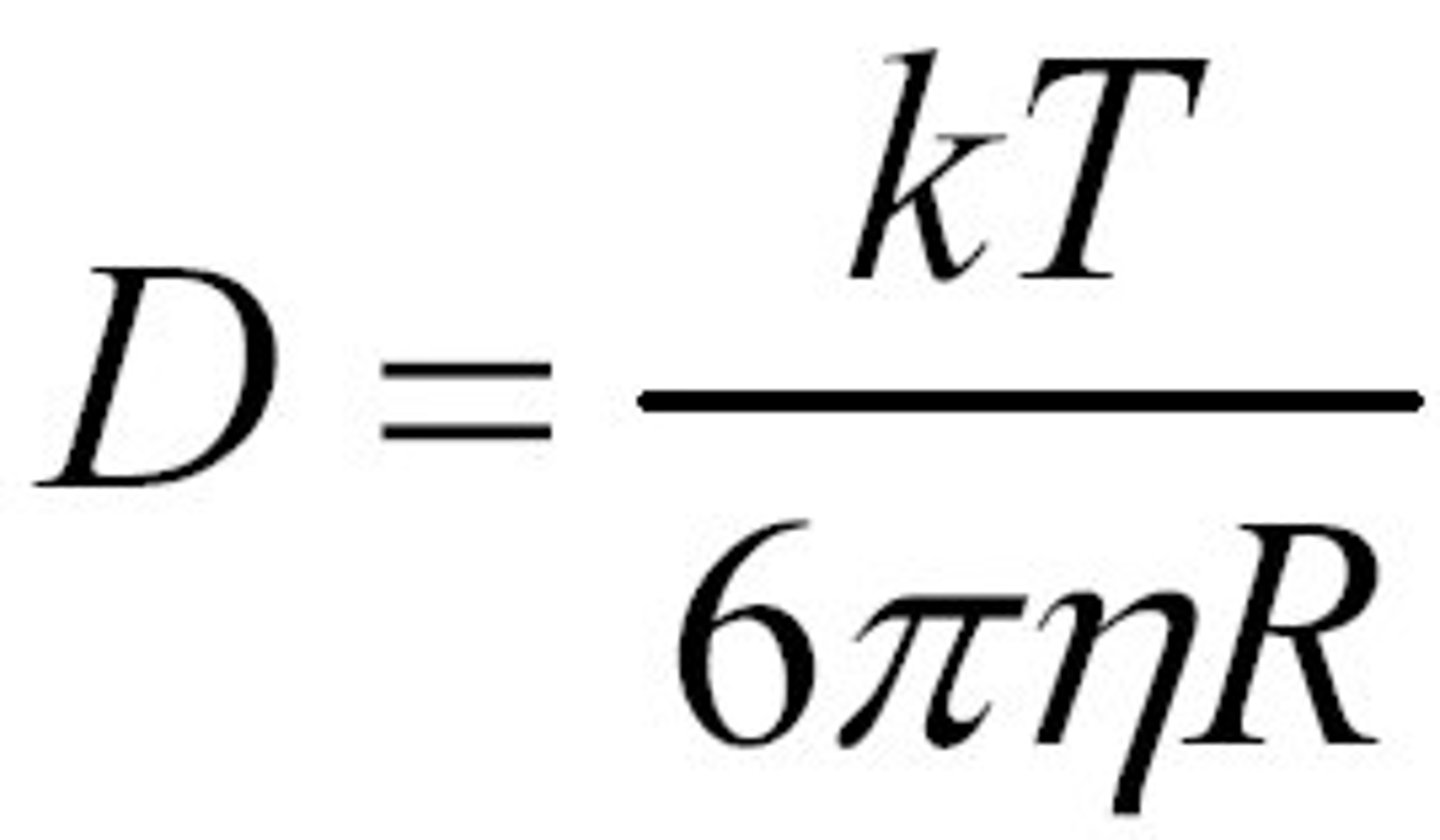
Measurement of the absorption spectrum.

Is a measurement of absorbance (log(J0/J)) vs wavelength of incident light.

The absorption maxima (can be more than 1) related to the electron excitation energy (E2-E1) which is characteristic for the molecular structure.

Electrons of the atom are quantized. Thus, to change their energy state, the incident light is required to be in a certain frequency (energy):

E2-E1 = ε = hf = h(c/lamda)

*we can use absorbance to find conc. of diluted solution (beer lambert law)

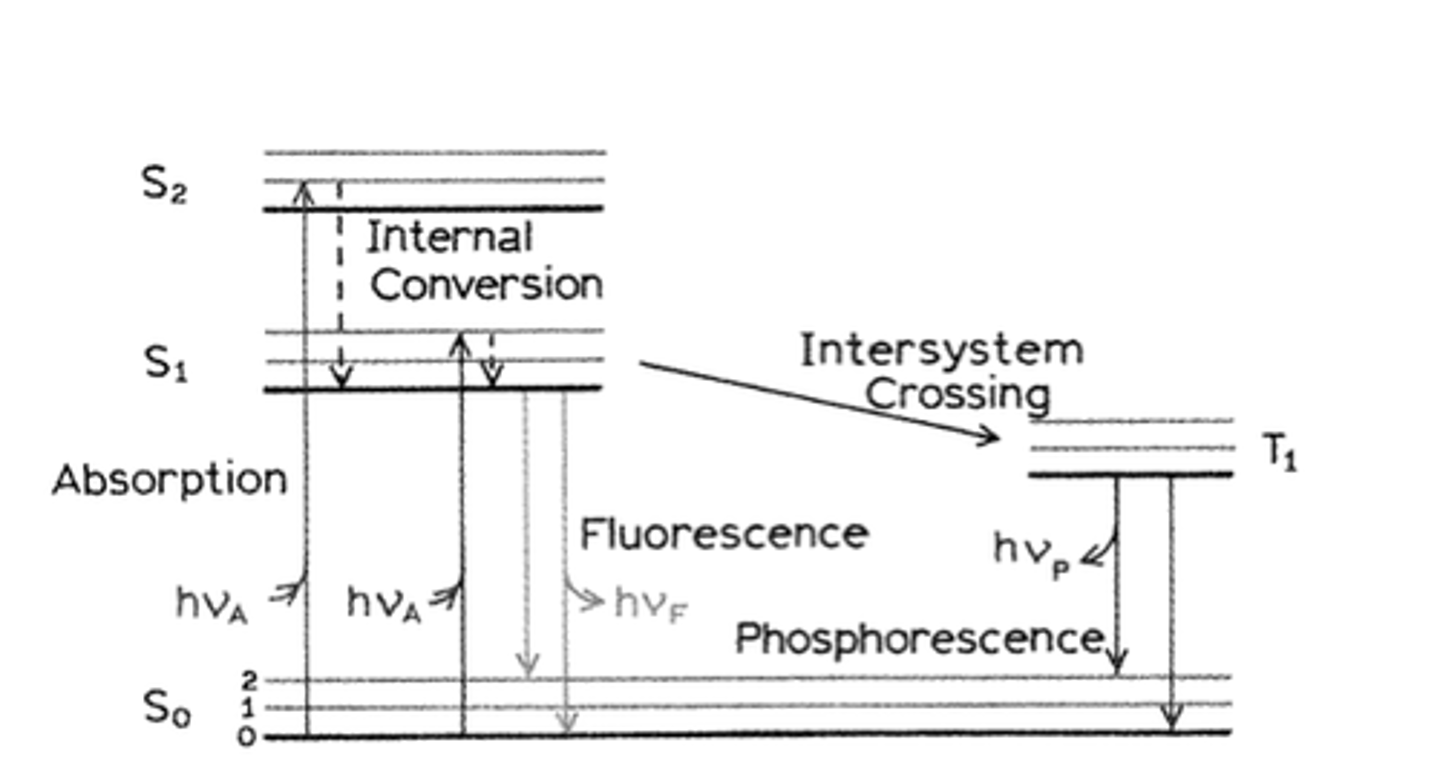
Energy levels of atoms and molecules: the Jablonski diagram

The diagram depicts the ground state which electrons strive to be on, and the excited states to which electrons can jump to if given the correct energy quanta.

Excited electrons will undergo "internal conversion" in which they rotate and vibrate until they reach a semi-stable state S1 (following Kasha's rule), only from that state will they relax to the ground state.

If they emit light during this relaxation it is called fluorescence.

Intersystem crossing occurs when the electron jumps to the triple state.

From the triple state to the ground state radiative relaxation is termed phosphorescence (slower process).

Thermal radiation.

Transfer of heat by using EM radiation → possible even in vacuum.

Every matter above 0K radiates thermal radiation.

Planck's radiation law:

By studying the emission spectrum of black bodies, Planck introduced the concept that the energy emitted resulted from the vibration of atoms within the material.

The vibrational energies have ​discrete values​(quanta=1,2,3), never a value in between.

If the oscillator changes from E1→ E2, the difference between those energy states will be emitted.

E2 − E1 = h * f .

h​​= p​lanck's constant

Light sources based on thermal radiation.

sun, light bulb, heated metal (at first will glow in red and after further heating will change to yellow and blue = wien's law.

Mblack(T)=sigmaT^4

Absolute black body.

An ideal, theoretical ​body which absorbs all the radiation incident on it and rememits it.

A model can be created from a closed metal cavity with a hole drilled into it, so radiation energy cannot easily escape, thus it is absorbed completely.

(Absorption coefficient of Stefan-Boltzman law​describes that the emittance of a black body is proportional to the fourth power of the temperature: Mblack(T)=sigmaT^4

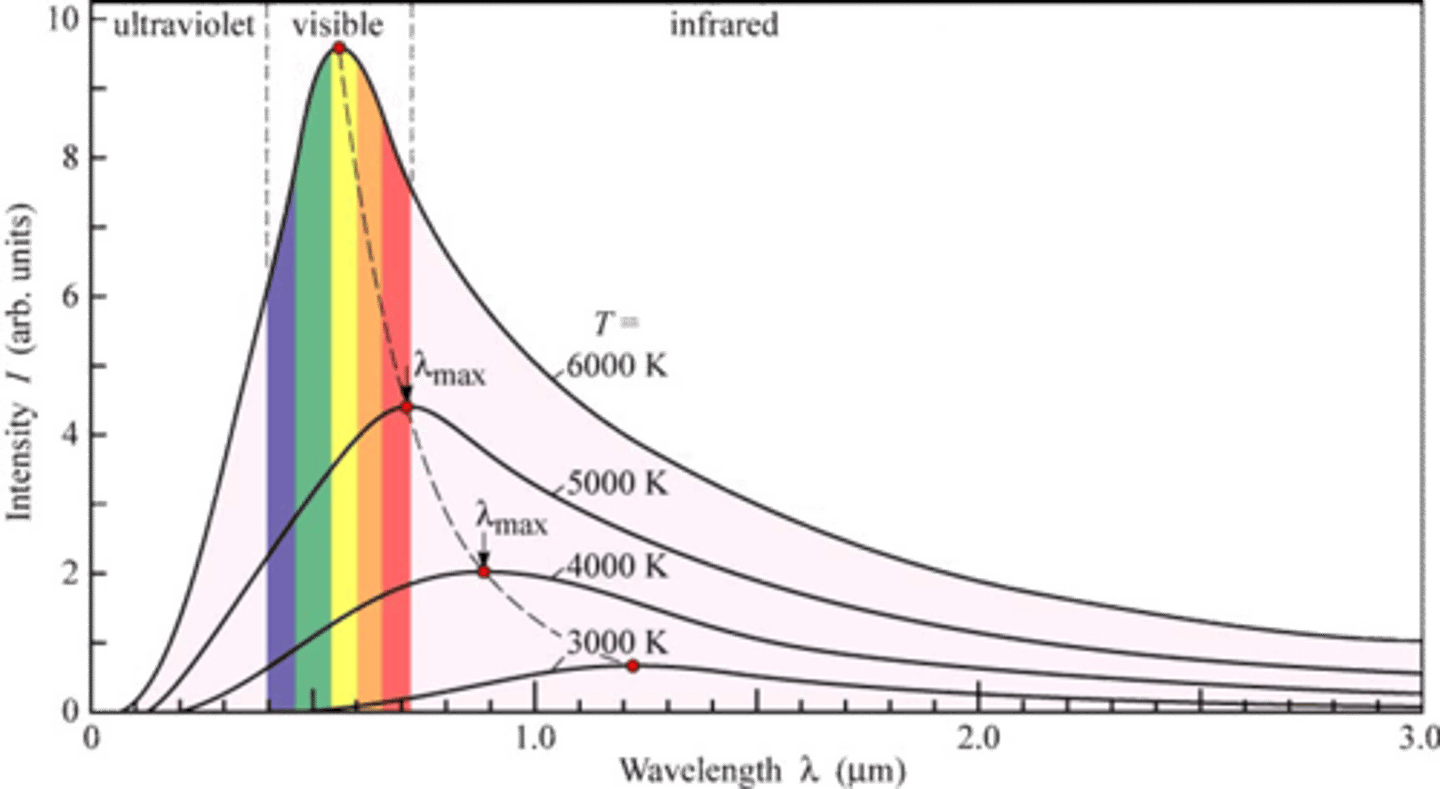
Emission spectrum of the absolute black body.​

The emission is in all wavelength spectrum. According to Wien's law, the maximum radiation is in wavelength that is inversely proportional to the temperature. wavelengthMaxT=constant.

At low temp. black body appears black- most of the energy it radiates is infra-red. when it getting how it will start to glow at first in red color and than in yellow and finally white-blue

- according to planck: radiation energy of a black body is emitted in discrete integer multiples. Quantum E = h*f

- according to stephan boltzmann:

Mblack(T) = sigmaT^4 describes the emittance of the black body as a proportion to temp. (fourth power proportionality)

Medical applications of thermal radiation.

Thermography i​s a test that uses an infrared camera to detect heat patterns and blood flow in body tissues. Digital infrared thermal imaging (DITI) is the type of thermography that's used to diagnose breast cancer.

(note. thermotropic liquid crystals are used here)

Kirchhoff's law.

States that a body which radiates more thermal energy is also absorbed thermal energy to a higher extent.

The ratio between radiant emittance and absorption coefficient is constant within a narrow range of wavelength

Mbody1/alphabody2 = Mbody2/alphabody2 = const

The Stefan-Boltzmann law.

Describes that the emittance of a black body is proportional to the fourth power of the temperature:

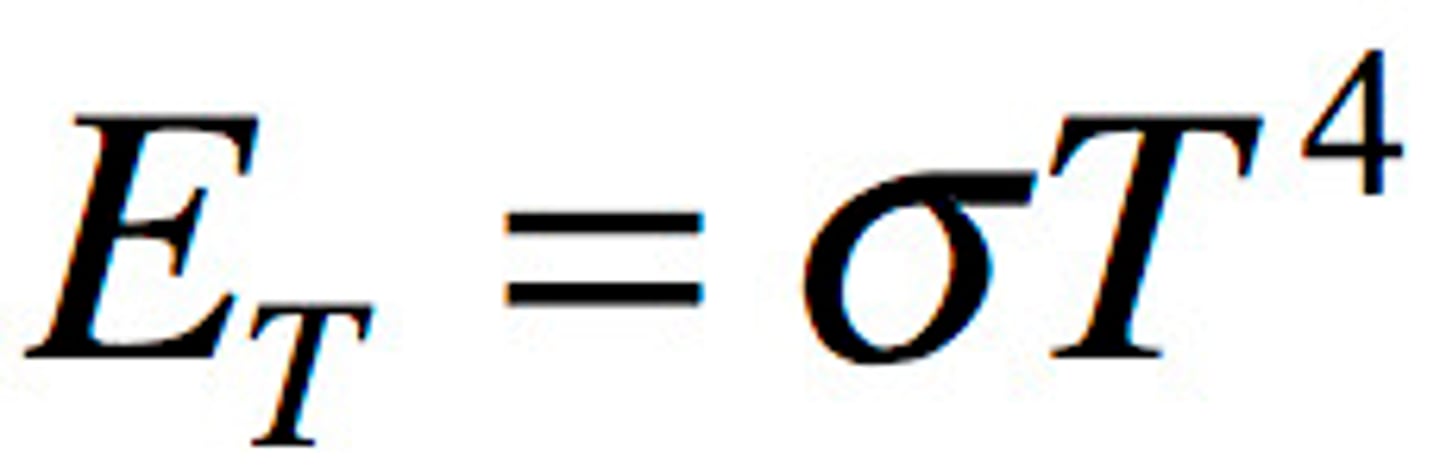
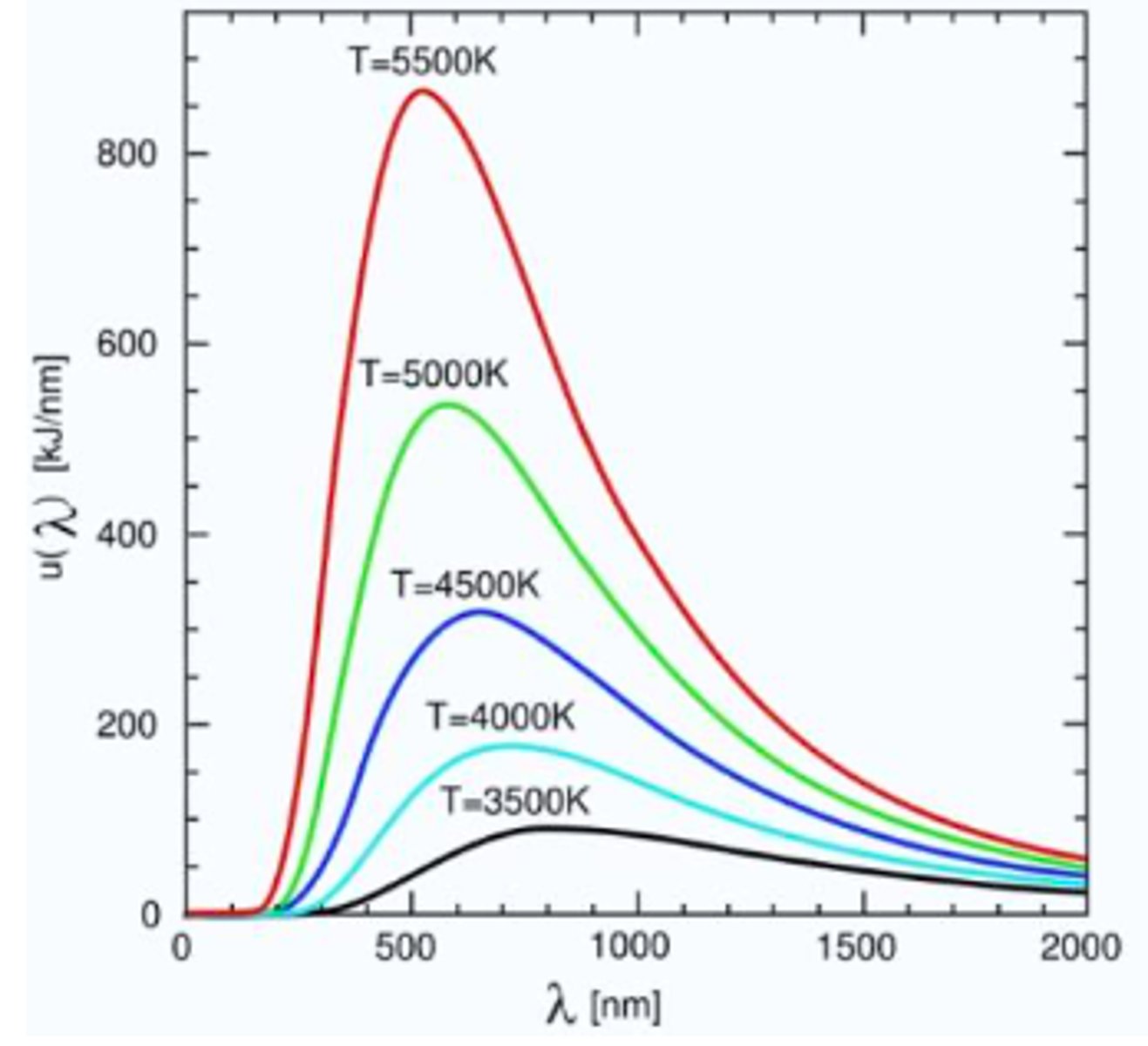
Wien's displacement law.

The black body radiation curve for different temp. peaks at a wavelength that is inversely proportional to the temp. ( high

temp.=low wavelength)

black body radiation v.s. wavelength curve:

Luminescence: excitation and relaxation.

The emission of excess energy, from excited electrons, in the form of light (cold emission, as opposed to thermal emission/incandescent emission).

Many types of excitation: thermo, bio, photo electron.

Process: Absorption of external energy → Excitation → Emission of energy in the form of light.

Types of relaxation:

Fluorescence:​ if the luminescence stops as the excitation stops (the relaxation step takes 10−8 seconds

Phosphorescence: ​if the luminescence continues for much longer (minutes).

Requires intersystem crossing into the triple state (from which there is a lower probability that the electron will relax).

Kasha's rule.

The excited molecule first reaches the lowest vibrational level of S1 and photon emission occurs always from this state to any vibrational level of the ground (S0) state.

Fluorescence.

is the emission of light by a substance that has absorbed light or other electromagnetic radiation. It's a form of luminescence.

In most cases, the emitted light has a longer wavelength, and therefore lower energy, than the absorbed radiation.

If the luminescence stops as the excitation stops (the relaxation step takes 10−8 seconds).

(Application: fluorescent lamps lasers, page 133)

Phosphorescence.

Occurs during transition from a triplet state to a ground state, a slower luminescence than fluorescesce. Phosphorescence occurs by excitation of electrons from ground state → vibration and rotation to the lowest excitation state) --> intersystemic crossing into a triple excited state→ returning to ground state by luminescence.

Luminescence spectra.

Atoms:​ line spectrum: due to Ephoton = E2 − E1 = h * f

Molecules: ​because discrete energy levels are split into vibrational levels, electrons will lose some of the excitation energy while they relax to ground state. This means there will be a spectrum of wavelengths that can be emitted.

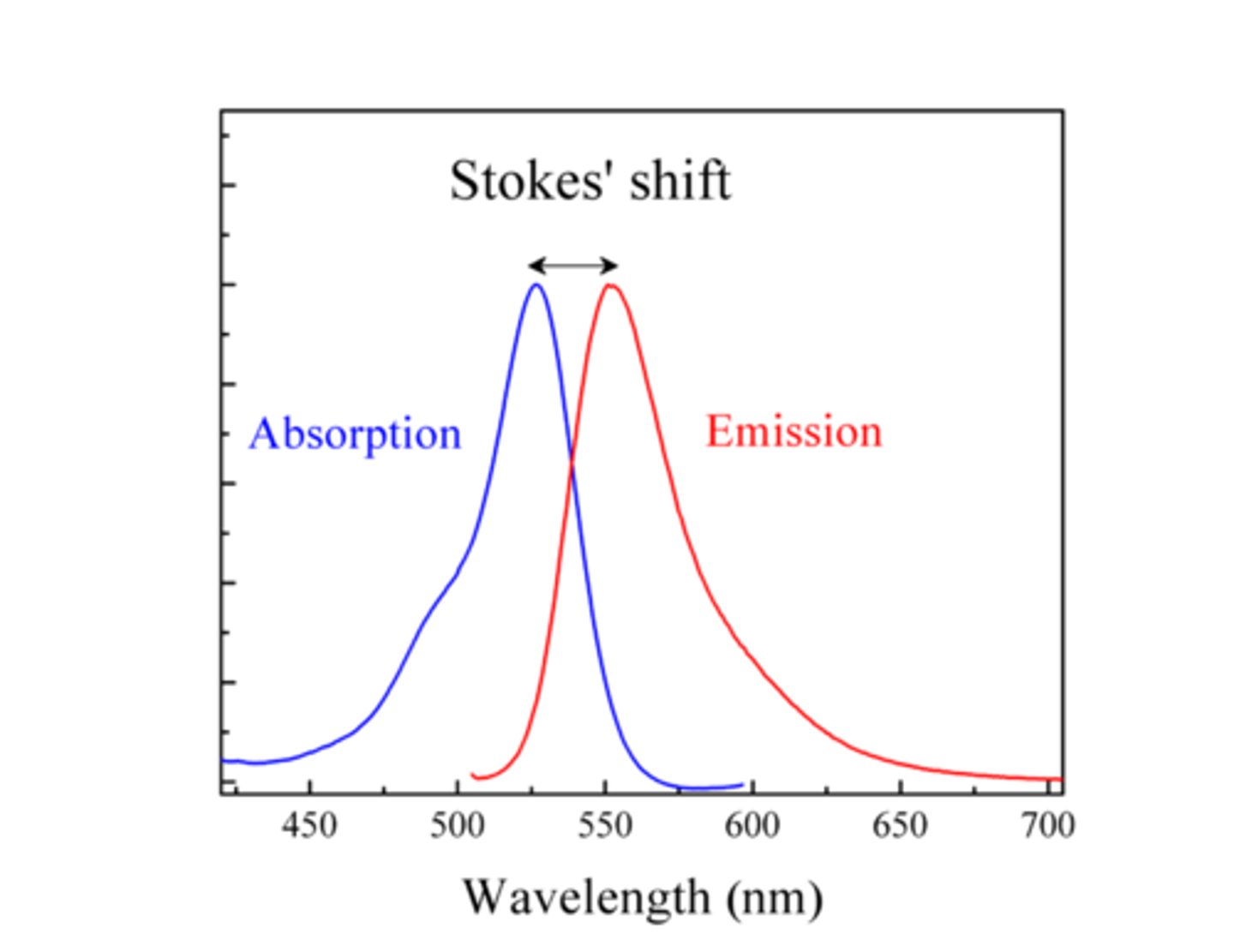
Stokes-shift

A shift difference btw. the peak absorption (excitation) and the peak of emission wavelength, due to loss of energy in form of heat (vibration and rotation of the molecule)

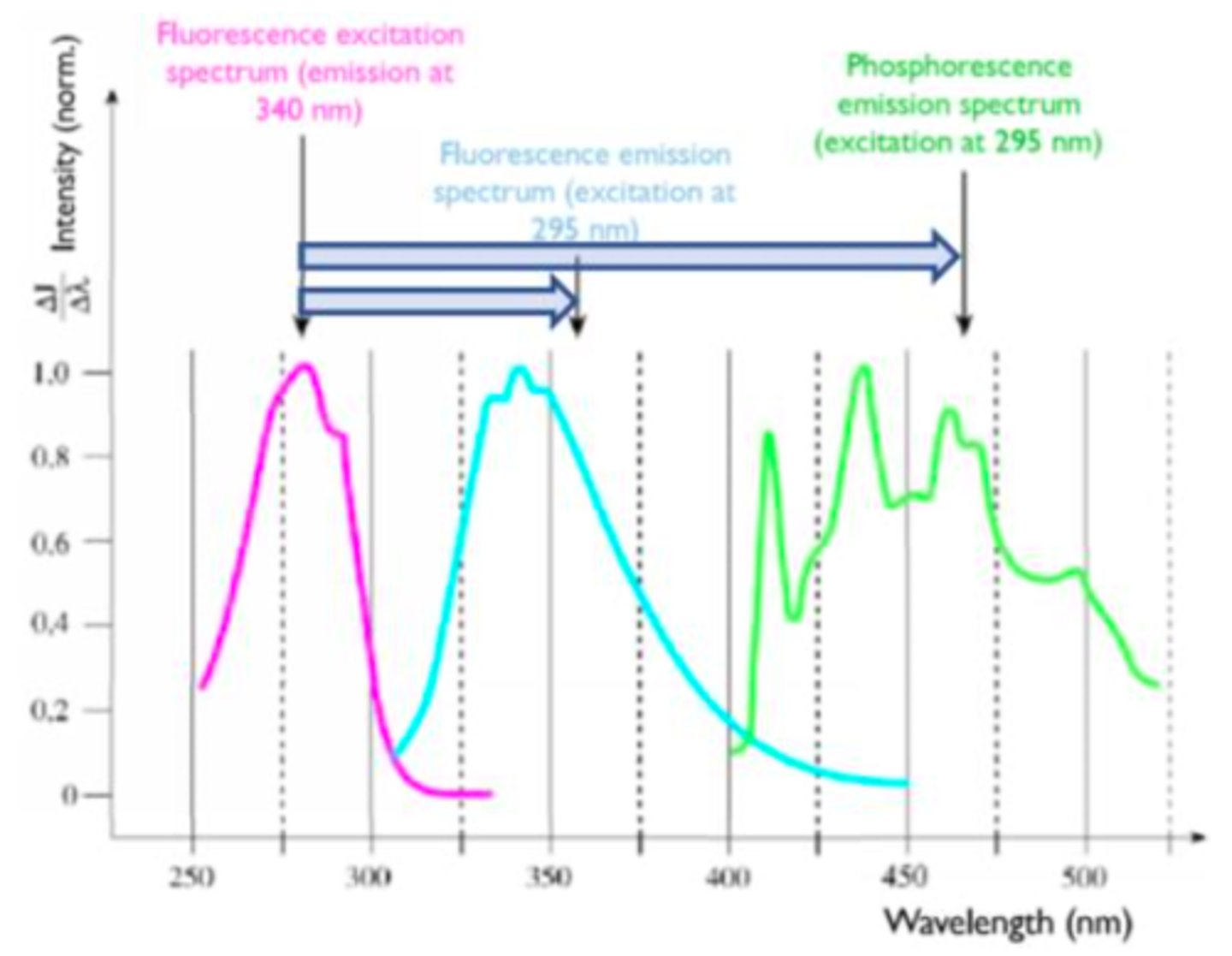
The fluorescence spectrometer.

A device which shines a light through a sample, measuring the excitation spectrum and the resulting emission spectrum.

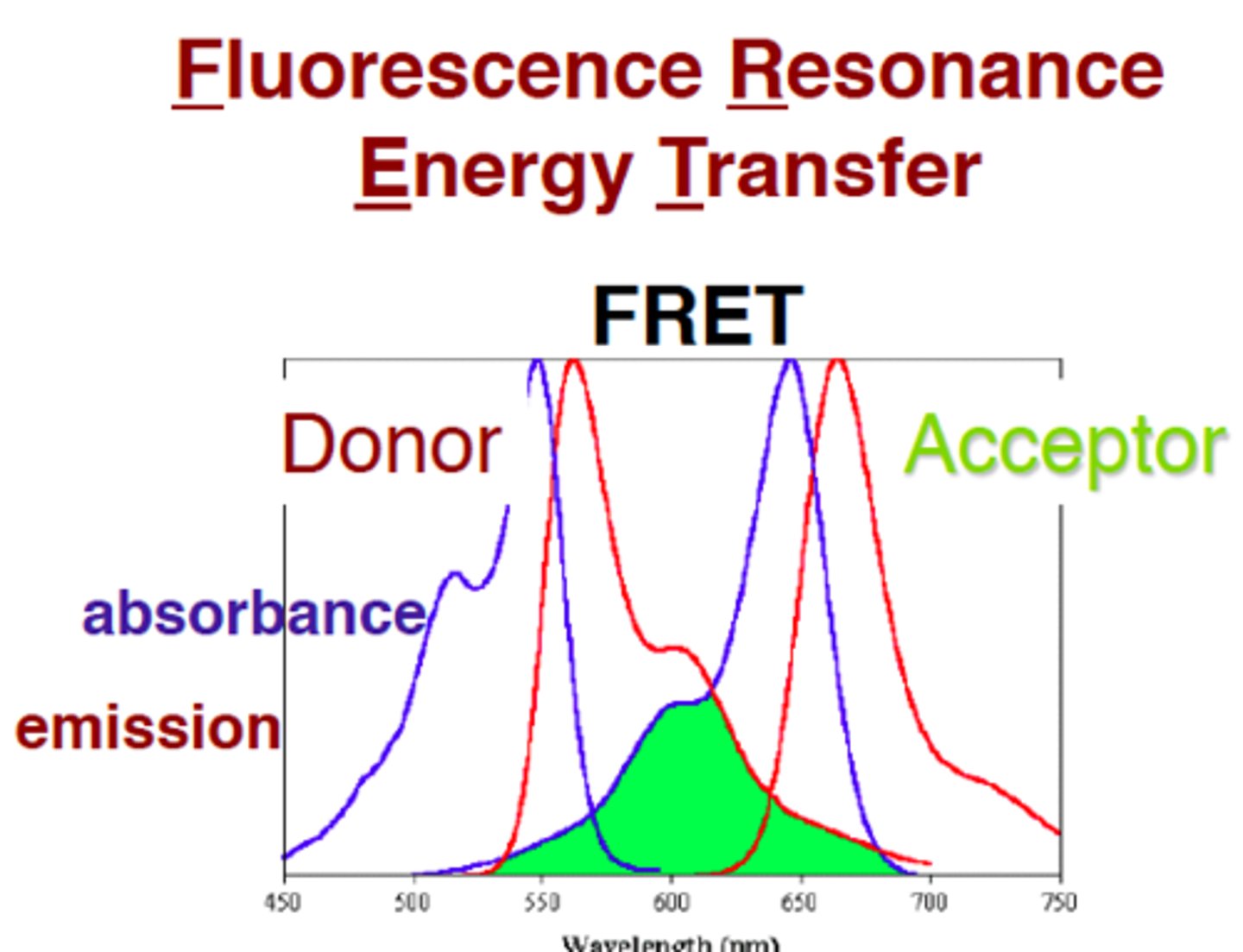
FRET. (Fluorescence Resonance Energy transfer)

Energy transfers from donor molecules, without emission, to acceptor molecules when they form dipole dipole interactions.

3 main requirements:

1. they have to be in the right orientation

2. they have to be really close (efficiency of the FRET is proportional to the r​eciprocal ​of the distance btw. the donor and the acceptor ​by the sixth power!​)

3. spectral overlap btw. donor and acceptor.

application: protein-protein interactions investigation

FRAP .

Fl​uorescence ​Re​covery after ​P​hotobleaching,

is used to study the diffusion of molecules on the lipid membrane.

The number of excitation and emission cycles is limited for fluorescent molecules, therefore they can be bleached.

When the previously bleached area of the membrane "recovers", this is proof of the lateral diffusion.

Notable transitions of luminescence: vibrational relaxation, intersystem crossing.

Vibrational relaxation: as kasha's rule states, an excited molecule will first reach the lowest vibrational level of s1, by vibration and rotation, losing energy in the form of heat (Ekin).

Intersystem crossing: occurs in phosphorescence, a process in which electron transition occurs btw. the singlet and the triplet state

(singlet and triplet state have different spin multiplicity [formula:2S+1])

*note: triplet has lower energy state than singlet

Quantum yield of luminescence.

Is a measure of the efficiency of photon emission through fluorescence, which is the loss of energy by a substance that has absorbed light via emission of a photon.

Defined as the ratio of the number of photons emitted to the number of photons absorbed.