Spontaneity and Entropy, Second Law: Physical Chemistry

First Law Review

∆U=q+w (conservation of energy)

Does the first law explain why gasses expand to fill a greater volume given?

Does the first law explain why heat flows from a hotter object to a colder one?

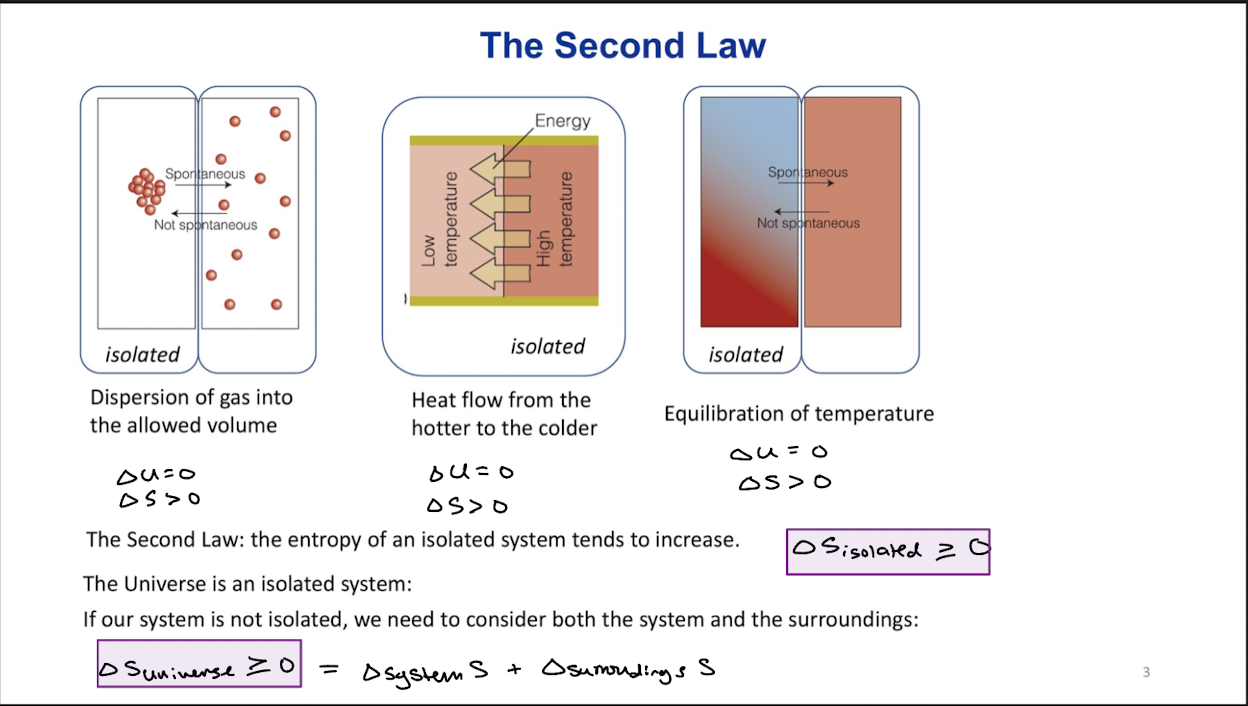
The First Law alone cannot explain the direction of spontaneous processes:

∆U=q+w is valid one way or the other

Classical mechanisms cannot explain the direction either:

There is no minimization of energy one way or the other.

The total energy, momentum, and angular momentum are conserved one way or the other (the principle conservation laws in classical mechanics).

Possible and impossible processes

It is impossible to construct a heat engine that converts all the heat it draws from they hot reservoir completely into work with no other changes in the surroundings.

1. Matter tends to disperse in diorder.

2. Energy tends to disperse in disorder.

Again, the First Law fails to explain these trends.

Also, how so such ordered systems as proteins and cells form?

It is impossible to convert all the thermal energy disordered into work (ordered).

Remember energy as heat is chaotic while energy as work is organized also

Second Law of Thermodynamics Reversible heat

Make the temperature of the hot reservoir slightly higher to barely allow the heat flow T₂~T₁

Let a small amount of reversible heat, q_rev, be added to a system at a temperature T. The change of entropy f the system: It is the thermodynamic definition of entropy.

Example: a cold-blooded organism dissipating heat into the surroundings it inhabits.

∆S= (q_rev/T)

Entropy change of physical processes: heating at a constant heat capacity

The entropy change of heating (or cooling) from T₁ to T₂

Heating (T₁ < T₂): ∆S>0

Cooling (T₁ > T₂): ∆S<0

∆S=m Cs In(T₂/T₁)

∆S=n Cm In(T₂/T₁)

∆S=C In(T₂/T₁) Constant heat capacity

Entropy Change of physical Processes: Constant Volume

∆S=n Cv In(T₂/T₁)

Entropy Change of physical Processes: Constant Pressure

∆S=n Cp In(T₂/T₁)

Entropy change of physical processes: if heat capacity varies

If heat capacity varies with temperature, there is no easy formula. Integrate C/T instead.

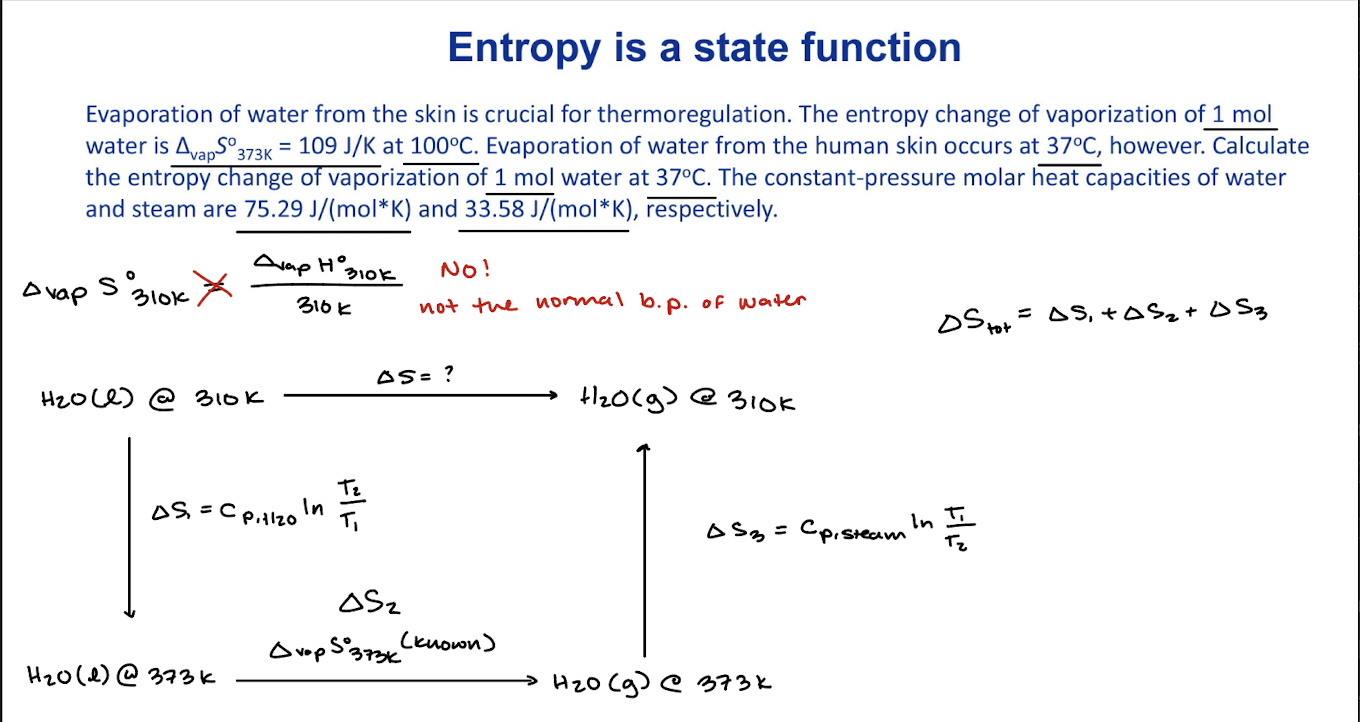
Unlike heat, entropy is a state function. ∆S depends only on the initial and final states, but not on the path taken.

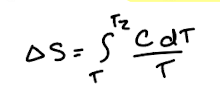
∆S of an ideal gas

∆S of isothermal expansion (quasistatic)

∆S=nRIn(V₂/V₁)

Only for ideal gas b/c ∆S is a state function

∆S=nRIn(V₂/V₁)+n Cv In(T₂/T₁)

Entropy change of physical processes: phase transitions

∆_fusS˚= (∆_fusH˚)/T_m

∆_vapS˚= (∆_vapH˚)/T_b

∆_tranS˚= (∆_tranH˚)/T_b

Entropy change in a spontaneous process

Second Law

Microscopic definition of entropy

The Boltzmann Formula

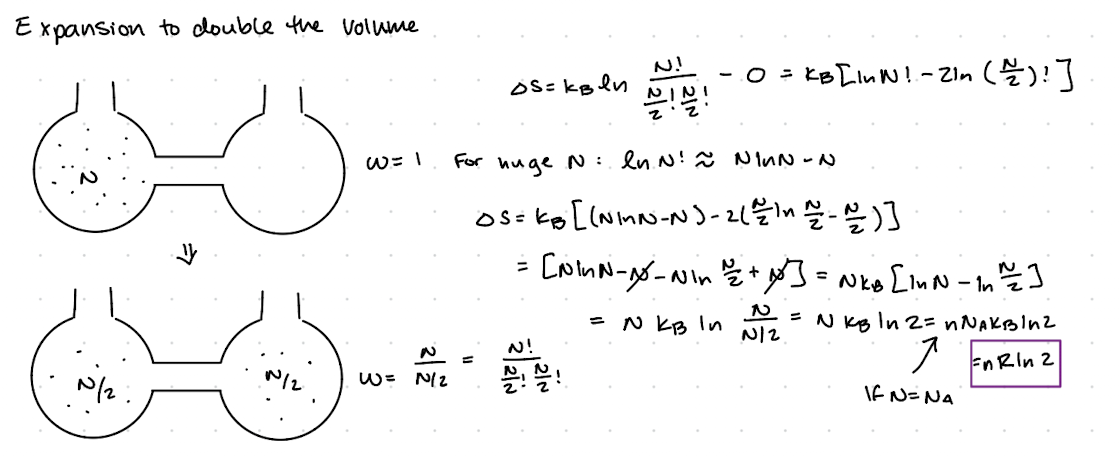
S=k_BInW

W= number of microstates consistent with macroscopic parameters (N,E)

W grows dramatically with the number of particles N and the total energy E

Spontatneous expansion of an ideal gas

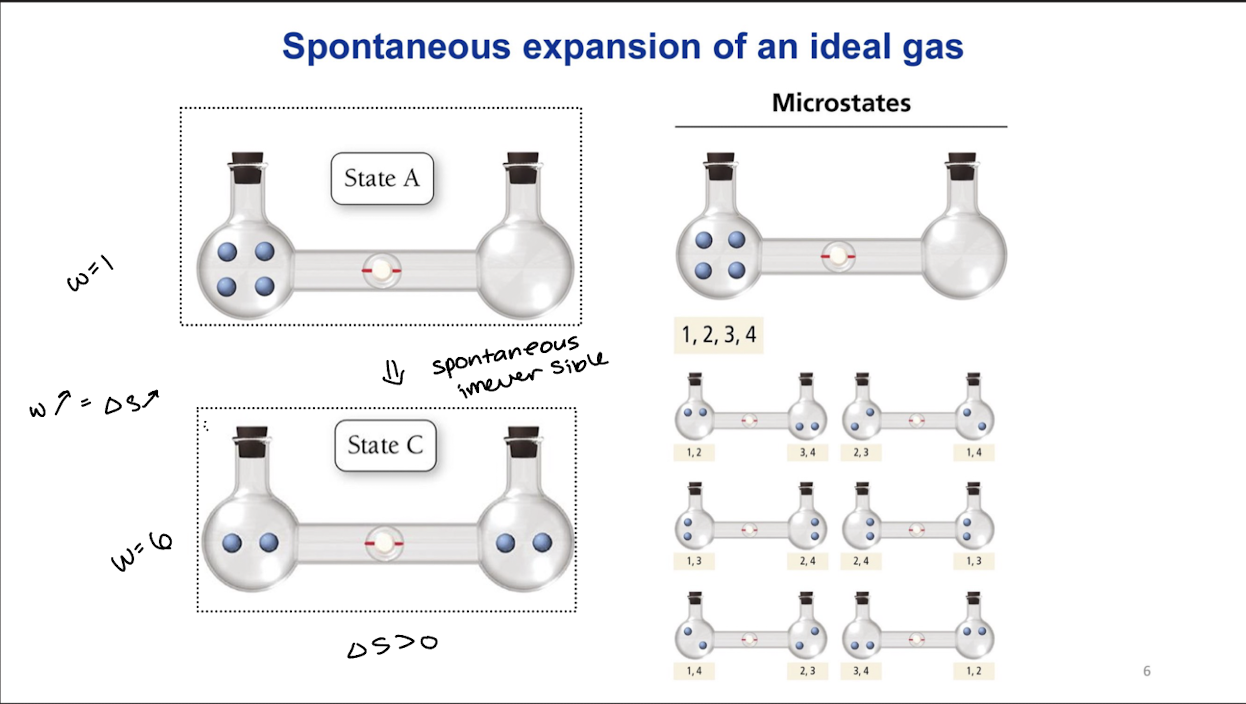
Expansion to double the volume