Microeconomics - uncertainty

Main concepts under uncertainty

• Expected value formula

• Expected utility

• Certainty equivalent

• Risk premimum

These are the main concepts you must be able to have FULL understand for to apply everywhere

• Possible monetary outcome(yi)

• Probabiliy of each outcome(pi)

Possible monetary outcome(yi)= monetary= related to money, means the differen money amouts that might happen where i can be anything from 1,2.., n

Probability of each outcome(pi) = tells you how likely each outcome is, where all probability must add up to 1, because something has to happen

Why does uncertainty come in

Many economic decisions involve uncertainty: outcomes are not known with certainty when choice is made.Example: a job offer may involve an uncertain future income, or an investment may have a risky return

Expected value

Is a way to summarize a risky situation by calculating the average outcome — if that situation were repeated many times.

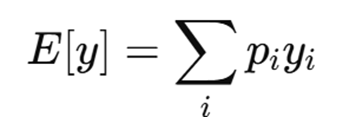
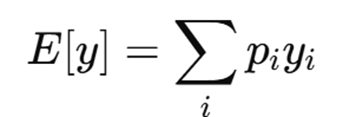
Explain this formula

• For each possible outcome, yi

• Multiply it by its probability, pi

• Then add up all of those results.

Expected utility

Under uncertainty, individual evaluate lotteries according to the expected utility of outcomes:

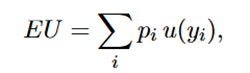
u(y): utility function representing preferences over wealth or income

Differance between expected value and expected utility

Expected Value (EV)
• EV is the average money outcome of a risky choice.
• Formula: EV = Σ pᵢ · yᵢ
→ Multiply each outcome yᵢ by its probability pᵢ, then add them up.
→ Focuses only on money, not feelings.

---

Expected Utility (EU)
• EU is the average satisfaction (utility) you get from a risky choice.
• Formula: EU = Σ pᵢ · u(yᵢ)
→ Multiply each outcome’s utility by its probability, then add.
→ Focuses on utility (happiness), not money.

Risk aversion

A person is risk-averse if they prefer the utility of a sure income over the expected utility of a risky income.

Condtion:u(E[y])>E[u(y)]

Basically they prefer a sure payment of 500 dollar than $1,000 with a probability 25 percent and $100 with a probability 75 percent, even if the average is both in same situations

What does this condition mean u(E[y])>E[u(y)]

• First calculate the expected value of the risky option.
  – Example: A lottery paying 4 million (50%) or 0 (50%)
  – EV = 0.5·4 + 0.5·0 = 2 million

• Compare:
  – Utility of the sure amount → u(2)
  – Expected utility of the lottery → 0.5·u(4) + 0.5·u(0)

A risk-averse person prefers:

• u(2) over 0.5u(4)+0.5u(0)

Meaning:

• They get more satisfaction from a guaranteed 2 million than from a 50/50 gamble between 4 million and 0 — even though both have the same expected value.

How does this explain a risk aversion person and there concave utility function

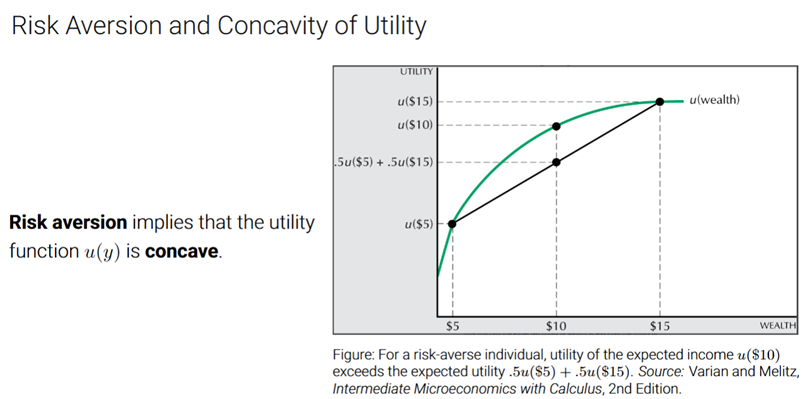
Risk aversion means the utility function u(y) is concave.
→ Each extra dollar gives less additional happiness than the previous one (diminishing marginal utility).

The graph shows:

• The green curve = utility function (concave) of getting the expectd income with certainty.

• The black curve = shows the risky gamble between two possible outcomes:

  • 50% chance of $5

  • 50% chance of $15

• Expected income:E[y] = 0.5(5) + 0.5(15) = 10

Look at $10 on the x-axis.

• The green dot = utility of getting $10 for sure

• The black dot = utility you expect from the risky gamble

Risk aversion condition: u(10)>0.5u(5)+0.5u(15)

.A risk-averse person prefers $10 for sure over a 50/50 gamble between $5 and $15 — even though both have the same expected value.

This happens because the utility curve is concave. Meaning they prefer the green line ALWAYS. Since the straight line = expected utility of the risiky lottery. Which is the average of the two utility points. For a risky person this point is below the green curve. Since the green curve is higher than the straight line, they prefer the green curve.

Certainty equivalent(CE)

The guaranteed amount of money that gives the same utility as a risky choice. Formula: u(CE)=E[u(y)]. Defines the guaranteed amount of money (CE) that gives the same utility as the risky option. Differs from Risk aversion condition that says you prefer the utility of the expected value over the expected utility of a risky

Risk premimum

The amount of money someone is willing to give up avoiding risky situations and get a guaranteed(certain) outcome instead

o   Formula: RP=E[y]−CE-

• E[y]= Expected value of the risky option

• CE= Certainty equivalent (what the person thinks gambling is worth)

It is bascially the extra value the risiky choice offer, but the person is to uncomfortable with risk, so they settle for less

What are the two assumed outcomes in the simplified uncertainty model?

A good state and a bad state, each occurring with 50% probability.

What is the expected income y^ in the two-state model?

The average of the good and bad outcomes.

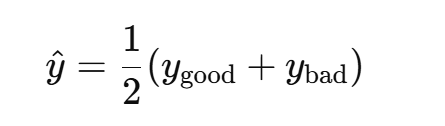
What is Δ?

Measures the risk. Shows the difference between good and bad outcomes. Higher differance→ more risk

Why is (ŷ, Δ) enough to describe risk?

• ŷ tells us the average outcome

• Δ tells us how risky it is (how far good and bad outcomes are from the average)

And since:

• only two outcomes

• with 50/50 probability

  • and symmetric around the average → the goods outcome is the same distance above the average as the bad outcome is below it. 

→ We don’t need anything else.
These two numbers fully describe the risky situation.

What is expected utility before simplification

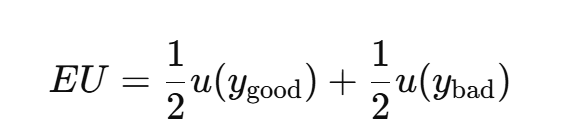
Why do we use reduced-form utility u(y^,Δ)

It simplifies expected utility when probabilities are 50/50 and outcomes are symmetric.
Utility becomes a function of:

• expected income y^

• risk Δ

Under what conditions can we reduce to u(y^,Δ)

• Two outcomes

• Equal probability

• Symmetric around mean

• Known concave utility function

• Risk is representated by Δ

What affects utility in the (ŷ, Δ) model?

• uy^>0 → higher expected income makes people happier

• uΔ<0→ more risk makes people less happy

So:

People want high average returns (ŷ ↑) but dislike big ups-and-downs (Δ ↑).

This simplified model is just a shorter way of expressing the same idea as a full concave expected-utility function

Formula for reduced form of utility

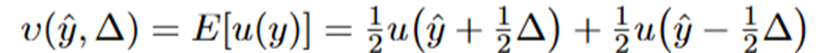
What does the indifferance curve under context of risk and expected income show

To understand how people make risiky choice we descrive their evalutions of different outcomes using utility function in which:

• Expected income is a good: something the decision maker prefers and wants more of.

• Risk is not a good: something the decision maker would like to avoid or is possibly indifferent to, but does not prefer

An indifference curve shows all combinations of risk (Δ) and expected income (ŷ) that give the same utility, so the person is equally happy at every point on the curve.

Slope - downward sloping

• More risk (Δ ↑) makes you worse off

• To keep utility the same, you must get more income (ŷ ↑)

So the curve slopes upward:
more risk → more income needed to compensate.

• Formula: Slope=−MRS=uΔ/ uŷ

  • vΔ<0: increasing risk reduces utility(bad)

  • vy^>0 increasing income increases utility(good)

• So:

  −(−/+)=+ slope is positive  - upward sloping

• Curves higher up represent more overall utility - you are better off, lower curves represent less utility 

  

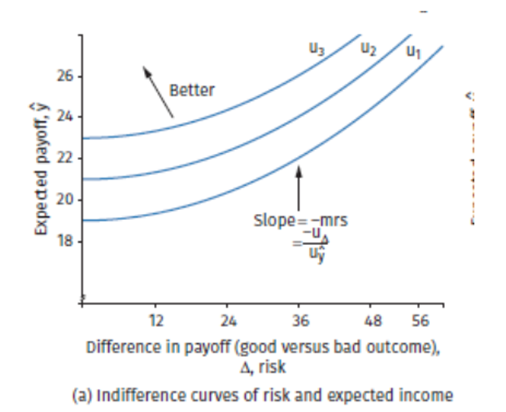
Remeber!

• Utility curve concave dimishing marginal utilitity is upward sloping but flattening, 

• In this graph we have different x-axis and y-axis, therefor different curves but both are upward sloping. Utility is just concave upward sloping and indiffferance curve upward slopiung

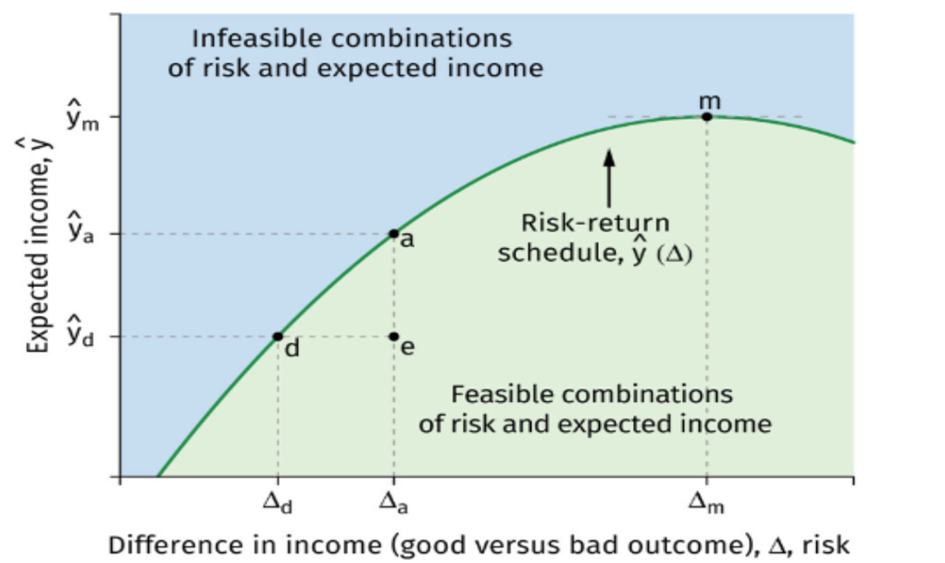
What is the risk-return schedule?

Shows how expected income changes when risk changes. Formula:

Think of it as:
“If I choose more risk (Δ), what expected income (ŷ) can I get?”

Differance between risk-return schudle and dimishing marginal utility curve

Diminshing marginal utility - how a person feel about wealth, thehuman psychology aspect of it. Concave utility curve

Risk-retun schedule - tradeoff between risk and income. Concave utility - similar in shape not meaning

Slope of risk-return schedule

MRT bascially

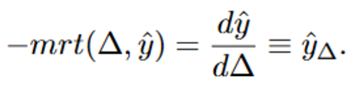
It tells you:

“If I change risk a tiny bit, how much does expected income change?”

What does a risk-averse person choose?

They use indifference curves, which slope upward because:

• More risk makes them worse off

• So they need more income to stay equally happy

The best choice is where an indifference curve is tangent to the frontier. This is point a in the graph, where MRS=MRT →

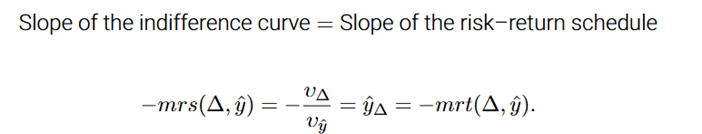
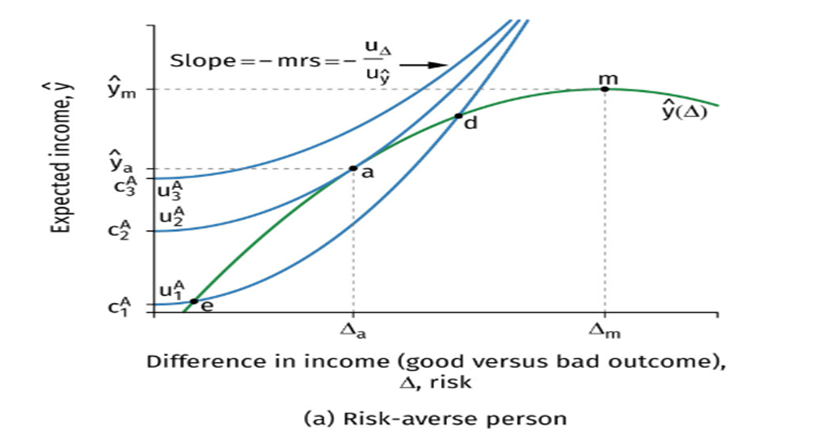
For a risk-averse person explain this pointers:

• Risk-return schedule

• MRT

• Indifference curves

• Optimal choice

Risk-return schudule: Shows the highest expected income possible for each level of risk.

MRT: Shows how expected income changes when risk changes.

Indifference curve: Show combinations of risk and income that give the same utility.

Optimal choice: tancency point where MRS=MRT

Is expected wealth the same as expected value

Yes expected value and expected wealth mean the same thing

What is a risk neutral person

A person that does not care about risk, they only care about expected return. They only want to maximize expected return and completely ignore risk.

Why CE < Expected return for a risk-averse person

Because of the concave utility: a risky outcome gives less utility than a sure outcome with the same mean. So the person is willing to accept a lower guanteed amount(CE)