Key Ideas

• Rotational kinematics uses essentially the same equations as kinematics, but distances, speeds, and accelerations are rotational quantities expressed with radians instead of with meters.

• Rotational inertia defines an object’s resistance to rotation.

• An object can possess rotational kinetic energy in addition to translational kinetic energy.

• Angular momentum is conserved anytime no external torque acts on a system of objects.

Rotational Kinematics

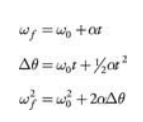
• In rotational kinematics, the units must be in radians and seconds

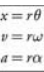
• r represents the distance from the spot we are interested in to the center of the object.

• The rotational kinematic equations are only valid when acceleration is constant.

Rotational Inertia

• Newton’s second law states that Fnet = ma

• The greater the mass of an object, the harder it is to accelerate.

• Tendency for massive objects to resist changes in their velocity is referred to as inertia.

• Spinning objects also resist changes in their angular velocity. This resistance is the rotational inertia.

• Rotational inertia depends less on the mass of an object than on how that mass is distributed

• The rotational inertia, I, is the rotational equivalent of mass.

• Tells how difficult it is for an object to speed up or slow its rotation.

• For a single particle of mass m a distance r from the axis of rotation, the rotational inertia is:

• To find the rotational inertia of several masses just add the I due to each mass.

Torque

• Torque occurs when a force is applied to an object, and that force can cause the object to rotate.

• The torque exerted on an object equals the force exerted on that object (F) multiplied by the distance between where the force is applied and the fulcrum (d) as long as the force acts perpendicular to the object.

• The unit of torque is the Newton meter.

  

Lever Arm

• The “lever arm” for a force is the closest distance from the fulcrum to the line of that force.

• Then, the torque provided by a force is the force times the lever arm.

Newton’s Second Law of Rotation

• The analog to Newton’s second law is:

  

where τnet is the net torque on an object.

• We have to draw a free-body diagram for the pulley as well as the blocks. Even though it doesn’t move, it still requires torque to accelerate its spinning speed.

• Because the pulley is massive, the tension in the rope may be different on each side of the pulley.

  

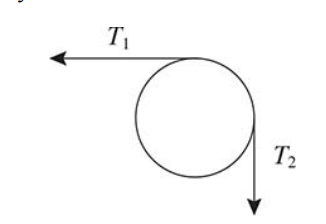
• For the pulley, because it is rotating, we write Newton’s second law for rotation.

• The torque provided by each rope is equal to the radius of the pulley, R.

• The acceleration of each block must be the same because they’re connected by a rope

• The linear acceleration of a point on the edge of the pulley must also be the same as that of the blocks.

• The R terms then cancel out, and the equation is simplified.

Rotational Kinetic Energy

• When an object is rotating, its rotational kinetic energy is found by the following equation:

  

• If an object is moving linearly at the same time that it’s rotating, its total kinetic energy equals the sum of the linear KE and the rotational KE.

Angular Momentum and Its Conservation

• Angular momentum is the amount of effort it would take to make a rotating object stop spinning

• An object with a large rotational inertia or with a high angular velocity (or both) would be pretty tough to bring to rest.

  

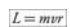
• v is the linear velocity

• r is either

  • the radius of rotation, if the particle is moving in a circle or

  • distance of closest approach if the particle is moving in a straight line

    

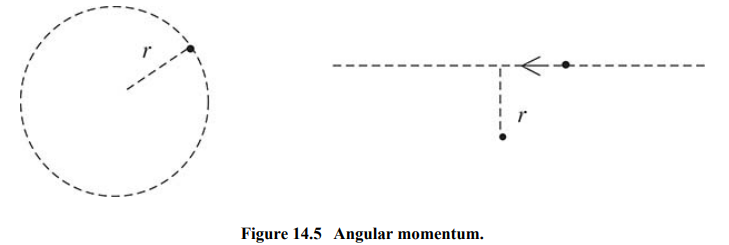
• If a particle moves in a straight line, then relative to some point P not on that line, the particle has an angular momentum.

• Angular momentum is conserved in a closed system; that is, when no external torques act on the objects in the system.