Simple Harmonic Motion

Key Ideas

• There are three conditions for something to be in simple harmonic motion. All are equivalent.
• The object’s position–time graph is a sine or cosine graph.
• The restoring force on the object is proportional to its displacement
  from equilibrium.
• The energy vs. position graph is parabolic.
• The mass on a spring is the most common example of simple harmonic motion.
• The pendulum is in simple harmonic motion for small amplitudes.

Amplitude, Period, and Frequency

• Simple harmonic motion is the study of oscillations.

• An oscillation is the motion of an object that regularly repeats itself over the same path.

• Objects undergo oscillation when they experience a restoring force: a force that restores an object to the equilibrium position.

• A restoring force doesn’t need to bring an object to rest in its equilibrium position; it just needs to make that object pass through an equilibrium position.

• The time it takes for an object to pass through one cycle is the period, abbreviated T.

  

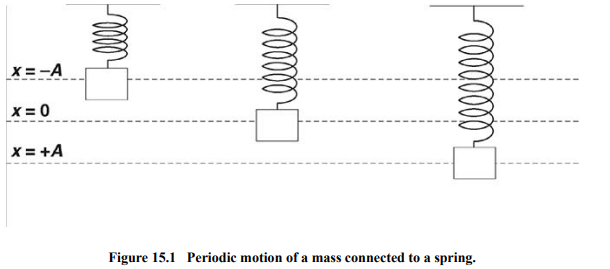
Vibrating Mass on a Spring

• A mass attached to the end of a spring will oscillate in simple harmonic motion. The period of the oscillation is found by this equation:

  

• m is the mass of the object on the spring

• k is the “spring constant.”

• To find the period, all we need to know is the mass.

• When dealing with a vertical spring, it is best to define the rest position as x = 0 in the equation for the potential energy of the spring.

• If we do this, then gravitational potential energy can be ignored.

Pendulums

Simple Pendulums

• the formula for the period of a simple pendulum is:

  

• L is the length of the pendulum

• g is the acceleration attributable to gravity

• the period of a pendulum does not depend on the mass of whatever is hanging on the end of the pendulum.

• To calculate the period of a pendulum, we must know the length of the string.

Compound Pendulum

• If the hanging mass has a size approaching the length of the string, the period of this “compound” pendulum is

  

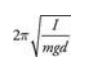
• I is the rotational inertia of the hanging mass

• m is the hanging mass

• d is the distance from the center of mass to the top of the string.

\
\