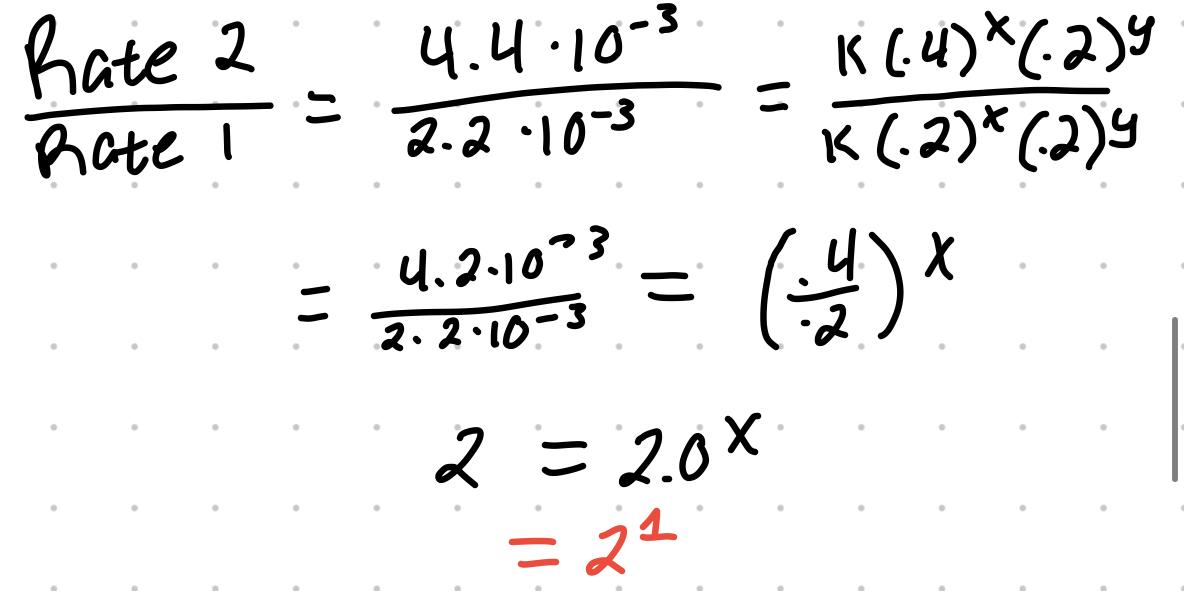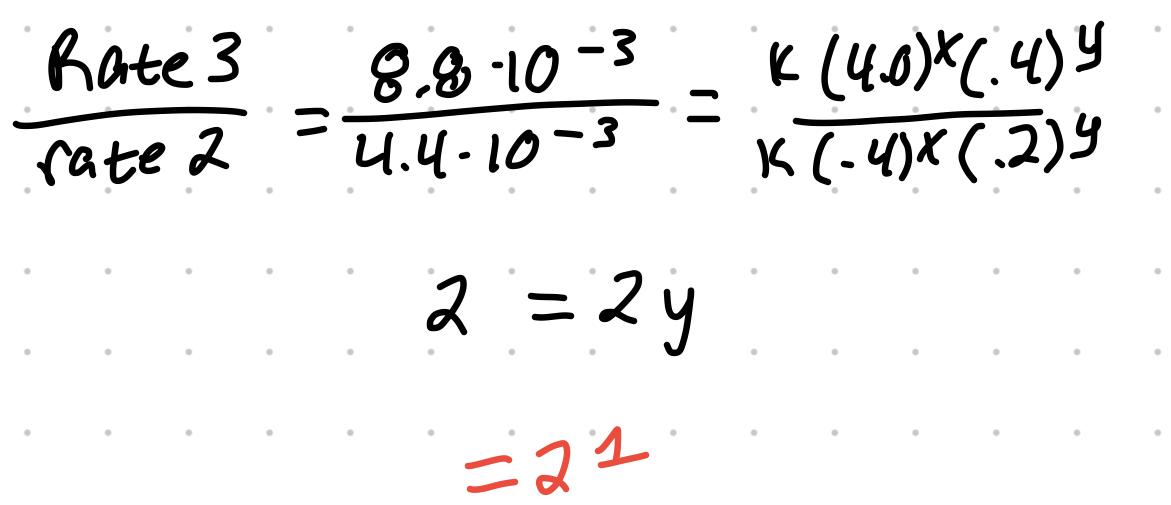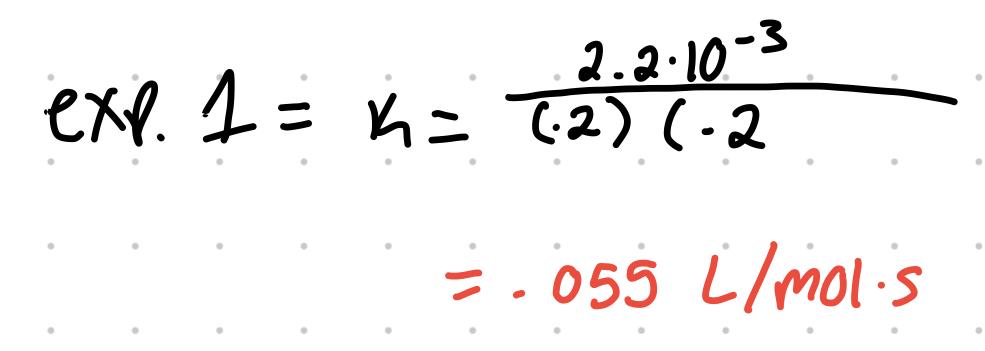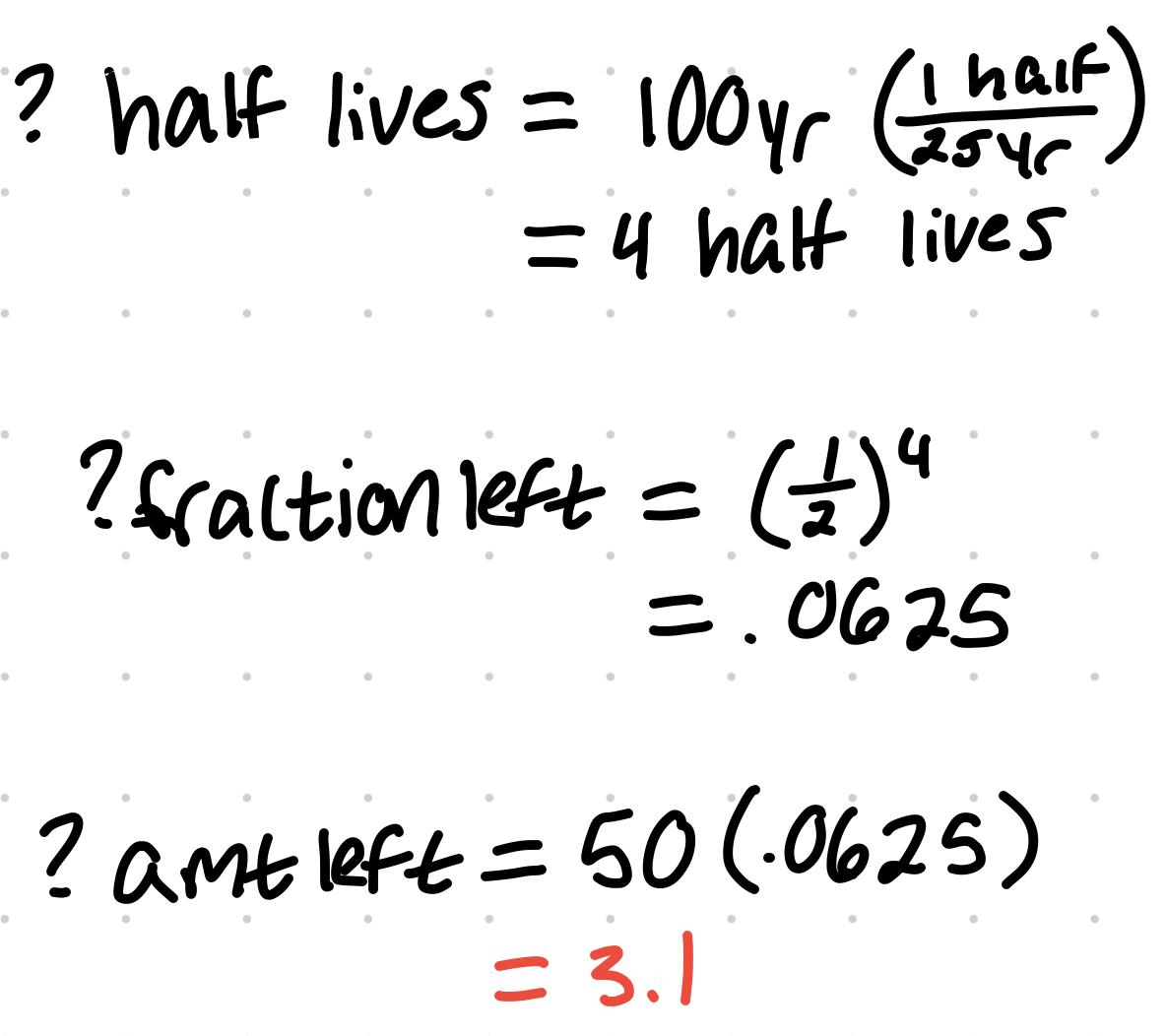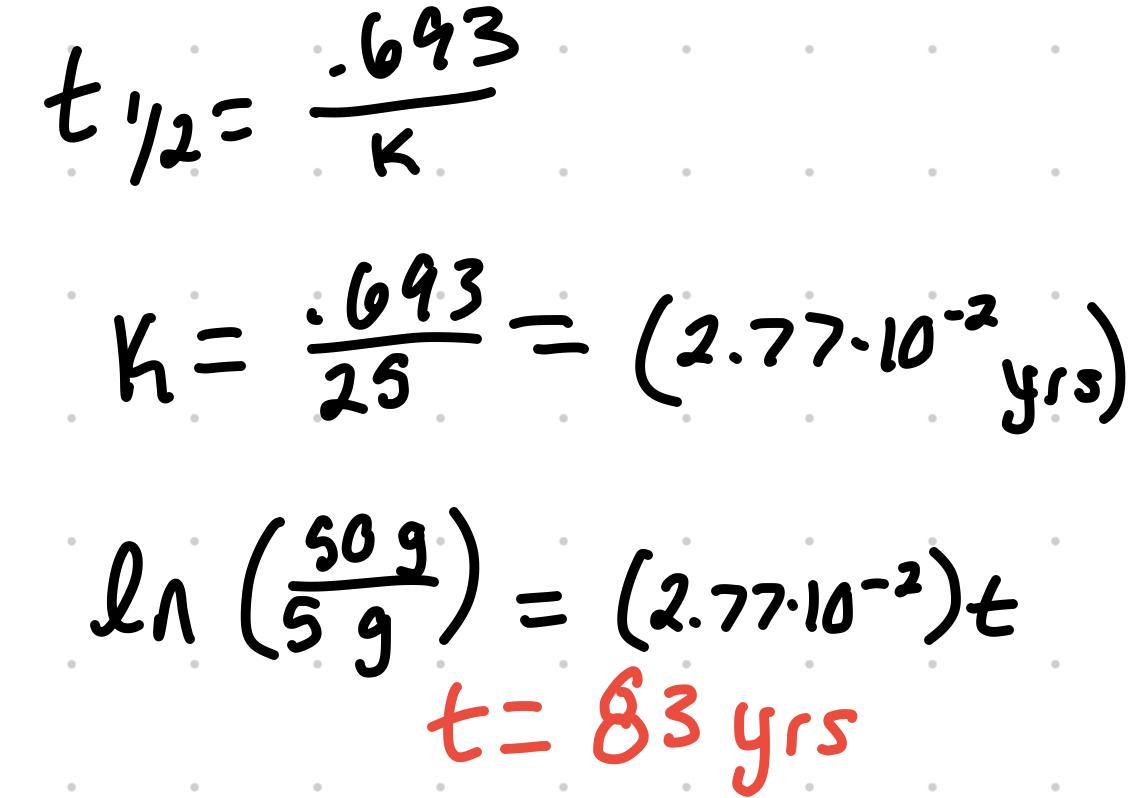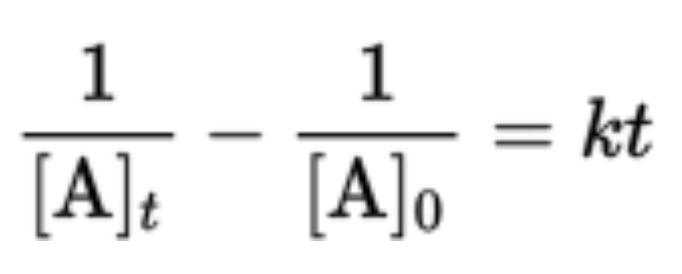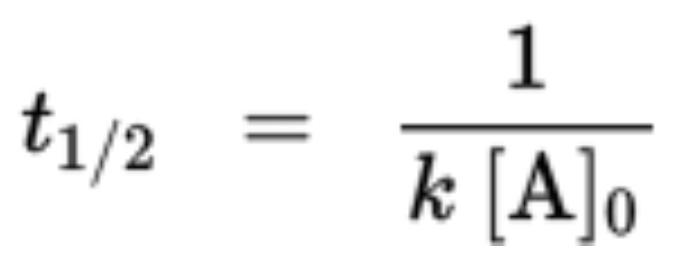Chapter 10: Kinetics
Reaction Rates
- Rate of a chemical reaction is the rate of change in concentration per unit of time, usually moles per liter that react each second.
- Reaction rates are determined by measuring the concentration of a substance at different times during a reaction
- A kinetic curve, or a concentration versus time curve, illustrates this
- Rate of product production (or reactant disappearance) is obtained by determine the slope of a kinetic curve
Factors That Affect Reaction Rates
- Concentration: If a substance is included in the rate law, increase the concentration (or pressure if a gas) will increase the reaction rate
- Temperature: exponentially related to Kelvin temperature
- Ability to meet: Gas or solutions react rapidly because of the individual molecules. Solids will react more rapidly if grinded finely
- Catalyst present: Catalysts lower activation energy and provide a larger rate constant
Concentration, Temperature, and Catalysts
- Similar to giving a car more gas to make it go faster, if the concentration of reactants is increased the rate will increase. Reactant concentration is directly related to the rate
- Temperature is carefully controlled in reactions because it changes the rate. Increasing temperature always increases reaction rate
- Catalysts increase reaction rate by lowering activation energy, or energy required for reaction to start. It does not appear in balanced equation
Effect of Concentration on Reaction Rate
- Rate law is the effect of concentration on a chemical reaction
- Rate = k[A]^x[B]^y[C]^z
- k is rate constant.
- exponents of the concentrations are determined experiementally, not through the chemical equation itself such as the coefficients
Determination of Rate Laws
- Changing the concentration of one reactant while holding the other constant can determine if that one reactant has an effect on the rate, and therefore the exponent
- For the reaction S2O8 + 3I- → 2SO4 + I3
| Experiment No. | [S2O8] (mol/L) | [I-] (mol/L) | Initial Rate of Rxn |
|---|---|---|---|
| 1 | .2 | .2 | 2.2x10^-3 |
| 2 | .4 | .2 | 4.4x10^-3 |
| 3 | .4 | .4 | 8.8x10^-3 |
This makes the rate law Rate = k[S2O8]^x[I-]^y
Experiment 1 and 2 can be used to find the exponent for S2O8 because I- is held constant
Experiment 3 and 2 can be used for [I-] exponent
To then find k, use the values from any ONE experiment and solve. any experiment values can be used.
Order of reaction is used to indicate the exponents in the rate law
- An exponent of one is first order. The reaction previously is first order with respect to peroxydisulfate and first order with respect to iodide ions
- It is second order overall because of the sum of the exponents
Effect of Temperature on Reaction Rates
- The Arrhenius equation defines the relationship between the rate constant and temperature
- k = Ae^(-Ea/RT)
- k is rate constant
- Ea is activation energy
- R is the universal gas constant = 8.314
- T is temperature in Kelvin
- A is a proportionality constant
- e is the base of natural logarithms
- ln k = (-Ea/RT) + ln A
- ln is natural log
- A larger rate constant wil always be associated with the higher temperature
- Activation energy always is positive
Applications of Selected Rate Laws
Zero-Order Reactions
- Zero order reactions have all exponents as zero
- Rate = k
- This reactions does not depend on reactant concentration
- Integrated rate equation is [A] = [A]0 - kt
- [A]0 is the initial
- Half life is t(½) = [A]0 / 2k
- t(½) is half life
First-Order Reactions
- First-order reactions have an exponent sum of one.
- Rate = k[A]
- As the concentration of A decreases, so does the rate
- If the concentration is half the initial, the rate will be half the initial rate
- This is the half life
The Integrated Equation
- The integrated first order equation is
- ln [A] 0 - ln [A]t = kt
- t is time
- k is rate constant
- [A]0 is initial concentration
- [A]t is concentration at some point in time
Half-Lives
- First order reactions have a constant half life
- t(½) = .693/k
- Most prominent first-order process is radioactive decay which follows first-order kinetics
Rate of Radioactive Decay
- After one half life, half of the isotope is left. After two half live, one quarter is left. After three half lives, one eighth is left
Radioactive Decay Calculations
The half life of Pb 210 is 25 years. In a sample of 50 µg of Pb 210, how much is left after 100 years
- 3.1 µg
How many years of 50 µg of Pb 210 takes to decrease to 5.0µg ( t(½) =25yrs)
- 83 years
Second-Order Reactions
Rate = k[A]^2
Rate = k [A][B]
Integrated rate law
Half-life equation
Theory of Reaction Rates
- Collision Theory: Rate of chemical equation is equal to the collision rate decreased by multiplying by an orientation factor and minimum energy factor.
- Transition State Theory: During the collision process, kinetic energy is converted to potential. If the potential energy exceeds or meets activation energy, the reaction occurs. The geometry of reactants changes as they become products, which is called the transition state as they convert from to the other and occurs when the max kinetic energy has been converted to potential energy
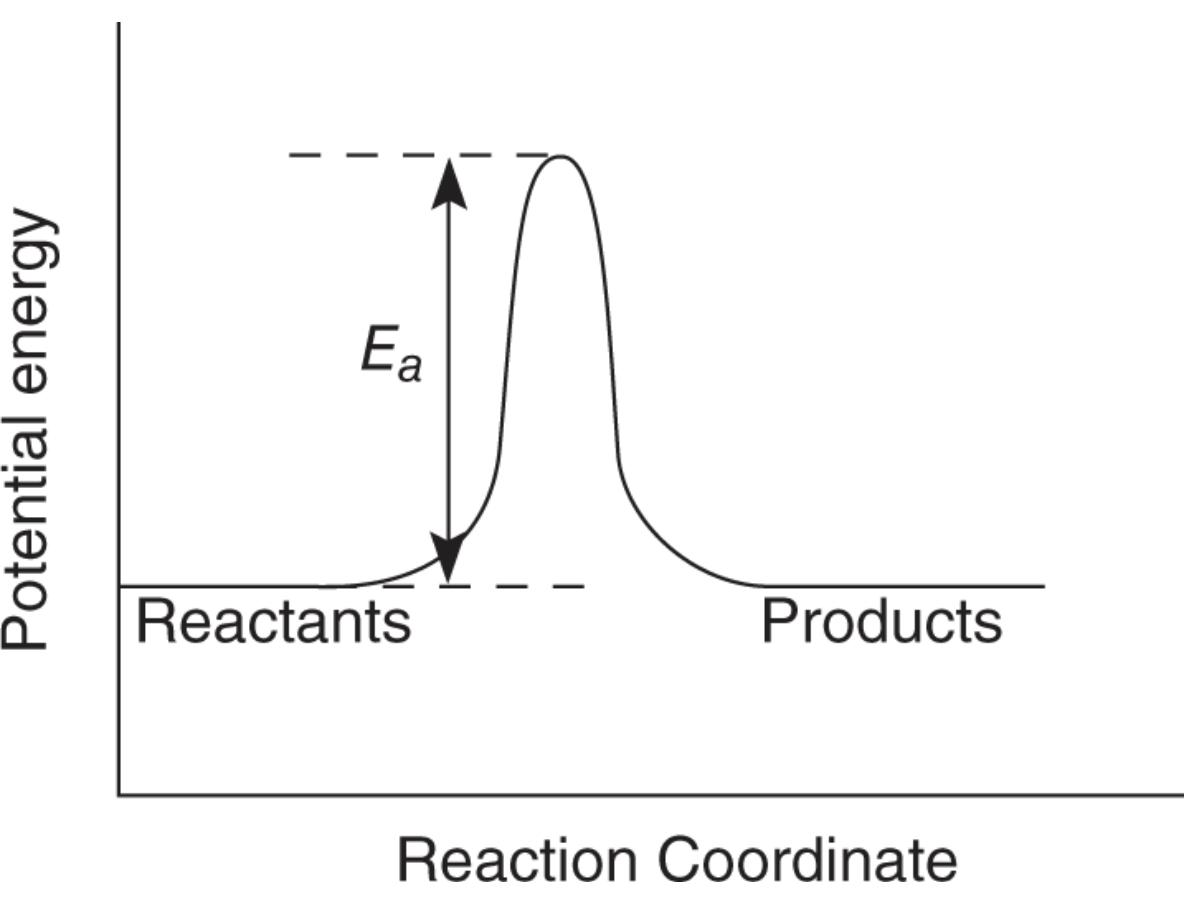
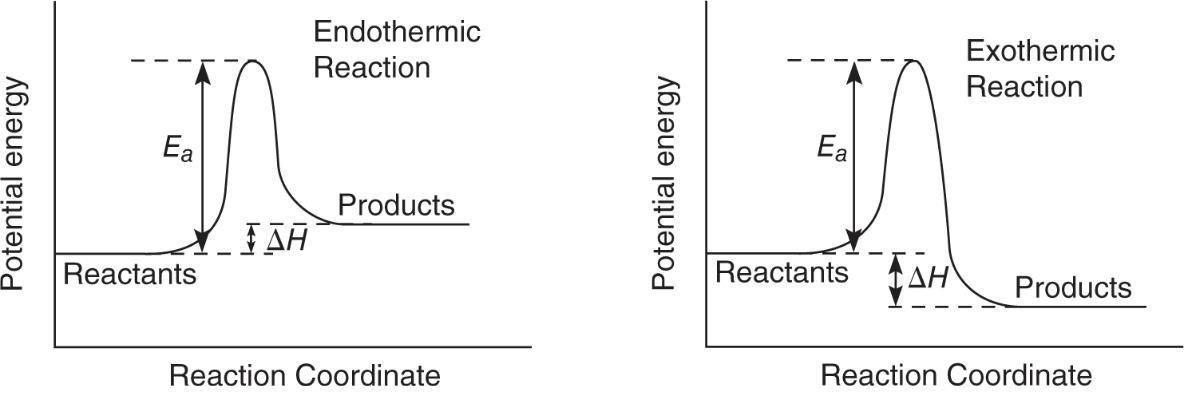
The Reaction Profile (Potential Energy Diagram)
According to the transition state theory, as molecules approach each other, they slow down and potential energy increases. After they get as close as they can, the potential energy decreases and kinetic increases.
The minimum amount of kinetic energy that must be converted is the activation energy
Interpretation of Reaction Profile
Reaction profiles help determine if a reaction is endothermic or exothermic.
Heat of reaction (ΔH) can be determine from potential energy of product and reactants
- ΔH = PE product - PE reactants
If ΔH is positive, heat is absorbed and is endothermic
- potential energy of products is greater than reactants
If ΔH is negative, heat is release and is exothermic
- reactants have more potential energy
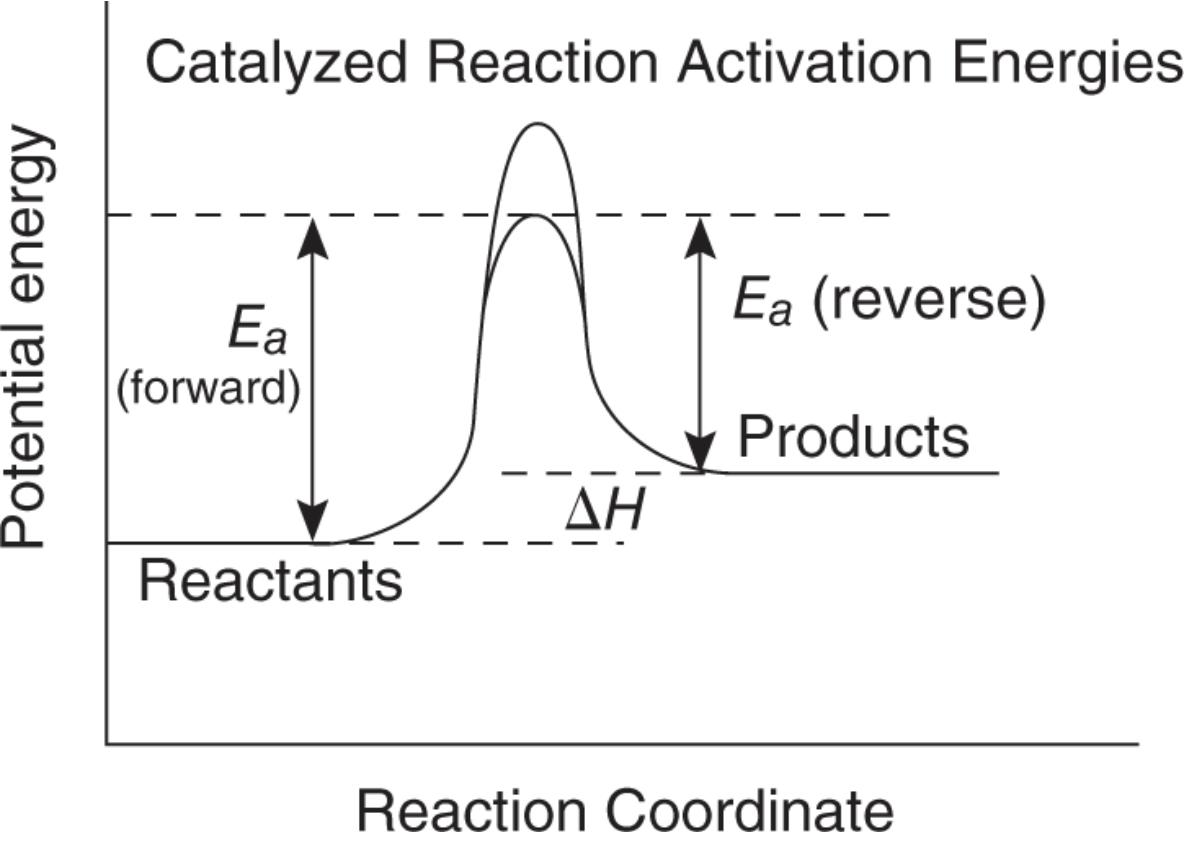
Catalysts allows a reaction to speed up by providing an alternate reaction pathway with a lower activation energy. However, this does not change the amount of product formed or the equilibrium concentrations.
Reaction Mechanisms
- Reaction mechanisms are the series of steps that occur in a reaction from start to finish. the steps in between are call elementary reactions which add up to the overall balanced equations
Elementary Reactions
- Elementary reactions are usually one or two molecules breaking apart of combining, rarely three. The coefficients are the exponents from the rate law
- The slowest elementary step is the rate-determining step, or the rate-limiting step.
- Example
- For the reaction H2 +2ICl → I2 + HCl with the rate law Rate = k[H2][ICl] it has the two-step mechanism
- H2 + ICl → HI +HCl
- HI + ICl → I2 + HCl
- The HI does not appear in the balance equation and is called and intermediate.
Determining the Rate Laws for Elementary Reactions
- Mechanisms with an intermediate in the slowest step must have the rate law adjusted to not include the intermediate in the rate law
- Example
- For the reaction 2NO + O2 → 2NO2
- NO + O2 → NO3
- NO3 + NO → NO2
- The rate for the first step is Rate = k [NO][O2]
- the rate for the second step includes and intermediate Rate = k [NO3][NO]
- The rate of disappearance and formation are opposite and equal, which gives the equation
- kf [NO][O2] = kr [NO3]
- kf is formation and kr is reverse
- Solve for NO3
- [NO3] = (kf/kr)[NO][O2]
- Substituting this into the elementary step rate law
- Rate = k (kf/kr)[NO][O2][NO]
- Combining the rates and rate constants
- Rate = k[NO]^2[O2]