4.4.2.3 Half-lives and the random nature of radioactive decay
0.0(0)
0.0(0)
Card Sorting
1/19
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No study sessions yet.
20 Terms
1
New cards
what do radioactive isotopes do
release radiation from the nucleus of their atoms
2
New cards
what is decay
a random process, which cannot be predicted
3
New cards
what is the half life of a radioactive isotopw
the time it takes for the number of nuclei of the isotope in a sample to halve
or the time it takes for the count rate (or activity) from a sample containing the isotope to fall to half its initial level.
\
It cannot be predicted when any one nucleus will decay, but the half-life is a constant that enables the activity of a very large number of nuclei to be predicted during the decay.
or the time it takes for the count rate (or activity) from a sample containing the isotope to fall to half its initial level.
\
It cannot be predicted when any one nucleus will decay, but the half-life is a constant that enables the activity of a very large number of nuclei to be predicted during the decay.
4
New cards
what is half life
the time it takes for half of the unstable nuclei to decay
the time it takes for the count rate or activity to halve
the time it takes for the count rate or activity to halve
5
New cards
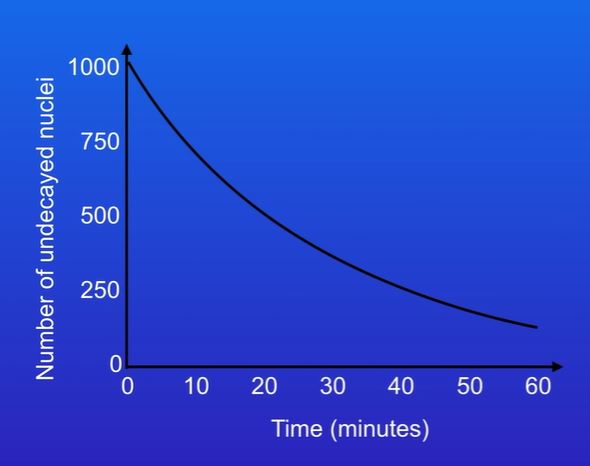
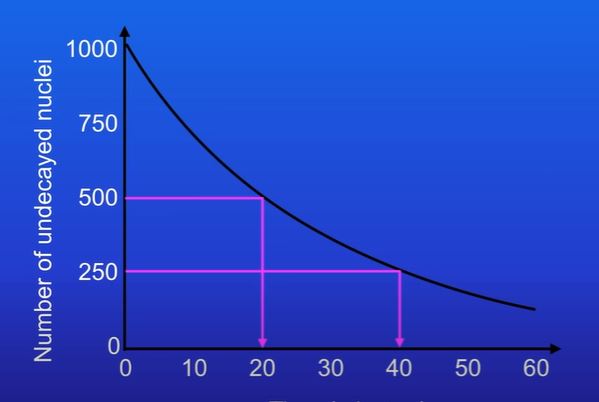
find the half lives of this graph
6
New cards


7
New cards
To calculate the half-life of a sample, the procedure is:
* Measure the initial activity, *A0*, of the sample
* Determine the half-life of this original activity
* Measure how the activity changes with time
* Determine the half-life of this original activity
* Measure how the activity changes with time
8
New cards
long half life
decays slowly
o The source remains weakly radioactive for a long period of time o Americium has a half-life of 432 years It is an alpha emitter, and used in smoke alarms It is emitted into the air around the alarm, and does not reach far because alpha is weakly penetrating If smoke reaches the alarm, the amount of alpha particles in the surrounding air drops This causes the alarm to sound o It is suitable because it will not need to be replenished, and its weak activity means it won’t be harmful to anyone
\
Long half-life, less active sample, stability is achieved after a longer time
o The source remains weakly radioactive for a long period of time o Americium has a half-life of 432 years It is an alpha emitter, and used in smoke alarms It is emitted into the air around the alarm, and does not reach far because alpha is weakly penetrating If smoke reaches the alarm, the amount of alpha particles in the surrounding air drops This causes the alarm to sound o It is suitable because it will not need to be replenished, and its weak activity means it won’t be harmful to anyone
\
Long half-life, less active sample, stability is achieved after a longer time
9
New cards
short half life
nuclei decay at a faster rate- wont take log for the number of the original isotope to halve
The source presents less of a risk, as it does not remain strongly radioactive
o This means initially it is very radioactive, but quickly dies down
o So presents less of a long-term risk
Short half-life, more active sample, less stable sample initially
Stability is achieved in a shorter time
The source presents less of a risk, as it does not remain strongly radioactive
o This means initially it is very radioactive, but quickly dies down
o So presents less of a long-term risk
Short half-life, more active sample, less stable sample initially
Stability is achieved in a shorter time
10
New cards
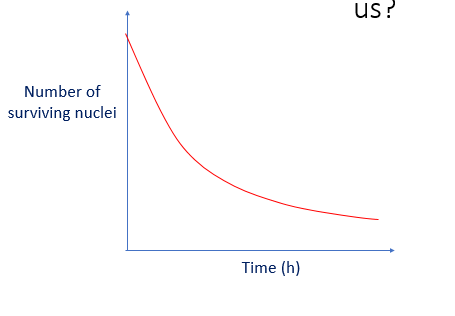
What does this graph show us?
•The number of surviving nuclei decreases with time
•Activity depends on the number of surviving nuclei so activity decreases with time
•The rate of decay is high initially but reduces with time
•In reality, activity never actually decreases to zero
•All radioactive samples produce the same characteristic graph shape
•Activity depends on the number of surviving nuclei so activity decreases with time
•The rate of decay is high initially but reduces with time
•In reality, activity never actually decreases to zero
•All radioactive samples produce the same characteristic graph shape
11
New cards
\- So if 80 atoms falls to 20 over 10mins, the half-life?
80/2 = 40 o
40/2 = 20
– so two half lives in 10mins
So half-life is 5mins
40/2 = 20
– so two half lives in 10mins
So half-life is 5mins
12
New cards
Net Decline
\- Calculate the ratio of net decline of radioactive nuclei after X half-lives o Half the initial number of nuclei, and keep doing so X number of times
\
\
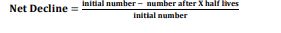
13
New cards
parctical method
1. count the number of nuclei in your sample to start and record this time at 0
2. throw them gently onto a tray
3. remove any that land with the ‘black side’ upwards- these are decayed nuclei. count the remaining ones and record them for each throw
4. each throw represents an hour of time. continue until they have all decayed
14
New cards
What is the relevance of half-life?
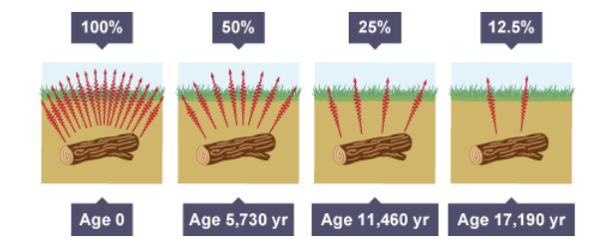
Carbon dating
All living things contain a tiny amount of the radioactive carbon-14
When living things die, they no longer absorb carbon-14
the amount of carbon-14 begins to reduce due to radioactive decay by beta decay
The half-life of carbon-14 is 5730 years
By measuring the levels of carbon-14 remaining in a piece of wood, cloth or body it is possible to determine the age of the item
All living things contain a tiny amount of the radioactive carbon-14
When living things die, they no longer absorb carbon-14
the amount of carbon-14 begins to reduce due to radioactive decay by beta decay
The half-life of carbon-14 is 5730 years
By measuring the levels of carbon-14 remaining in a piece of wood, cloth or body it is possible to determine the age of the item
15
New cards
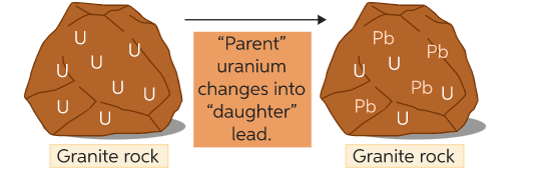
Uranium dating
•This is used to find the age of igneous rocks
•Igneous rocks with a half-life of 4500 million years
•Each uranium atoms decays into an atom of lead
•The age of the sample can be worked out by measuring the number of atoms of uranium and lead
•Igneous rocks with a half-life of 4500 million years
•Each uranium atoms decays into an atom of lead
•The age of the sample can be worked out by measuring the number of atoms of uranium and lead
16
New cards
Count rate after n half-lives=
(Initial count rate)/2^n
17
New cards
Activity after n half-lives=
(Initial activity)/2^n
18
New cards
Number of half-lives=
(Total time)/(Time taken for one half-life)
19
New cards
Net decline=
(Reduction in activity)/(Original activity)
20
New cards
Reduction in activity=
Original activity-final activity