Chapter 4 Test

Forces

Forces

pushes or pulls on an object

Contact Forces

there needs to be contacts for the force to cause motion; ex: friction, lift, air resistance

Non-Contact Forces

no contact is necessary for motion to occur; ex: gravity, magnetism

Newton’s 1st Law of Motion name

Law of Inertia

Newton’s 1st Law of Motion stated

an object in motion will remain in motion, an object at rest will remain at rest, unless acted upon by a net external force

Newton’s 1st Law of Motion net force

ΣF; vector sum of all forces

Newton’s 1st Law of Motion mass

intrinsic value that is a quantitative measure of inertia (doesn’t change based on where we are)

Newton’s 1st Law of Motion Inertia

tendency for an object to remain in its state of either motion or rest

Newton’s 2nd Law of Motion name

Law of Acceleration

Newton’s 2nd Law of Motion Stated

when a net external force, ΣF, is applied to a mass, m, it imparts acceleration a; ΣF=ma = kg*m/s² = Newton (N)

Newton’s 2nd Law of Motion units

Si- kg, m/s², Newton; CGS- gram, cm/s², dyme (dyn); BE- slug, ft/s², lb

Newton’s 2nd Law of Motion Free Body Diagram

diagram that represents the forces acting on a single object; place a dot to represent the object, construct an xy axis with the dot as the origin, and draw and label forces using size appropriate arrows

Newton’s 3rd Law of Motion name

Law of Reciprocal Actions

Newton’s 3rd Law of Motion stated

when one body exerts a force on another body, the second body exerts a force equal in magnitude but opposite in direction to first

Newton’s 3rd Law of Motion examples

swimming

Newton’s Law of Universal Gravitation stated

every particle in the universe exerts an attractive force on every other particle based on F_g= (G*m₁m₂)/r²

Newton’s Law of Universal Gravitation equation

F_g= (G*m₁m₂)/r²; F_g- force due to gravity; G- universal gravitational constant; m₁- mass of object 1; m₂- mass of object 2; r- distance between the object’s centers

Universal Gravitational Constant

6.67 × 10^-11 Nm²/kg²

Significance of [G(m/r²)]

acceleration due to gravity; determines the gravity of a planet; is F_g = m * g when objects are close to a planet’s surface

Pound → Newton

1 lb → 4.45N

Kilogram → Newtons

kg * gravity

Normal Force (F_N)

a component of force that a surface in contact with something exerts perpendicular to itself; opposite of gravity; without it we would accelerate downwards; if resting on horizontal, non-accelerating surface, F_N = F_g

Apparent Weight

weight displaed that is different than F_g that arises from either acceleration or a non-horizontal surface; F_N= F_g + F_applied = mg + ma; ex: elevator

Friction

component of force that acts parallel to a surface and opposes motion

Static Friction definition

F_s; force that must be overcome to set an object into motion; depends on coefficient of static friction and amount of Normal Force present

Static Friction equation

F_smax = μ_s F_N

Static Friction coefficient

μ_s; dependent on surfaces in contact

Kinetic Friction definition

F_k; force that must be overcome to keep an object in motion; depends on coefficient of kinetic friction and amount of Normal Force present

Kinetic friction equation

F_k= μ_K F_N

Kinetic Friction coefficient

μ_K; dependent on surfaces in contat

Friction on an incline F_g ≠ F_N

F_N = F_⊥

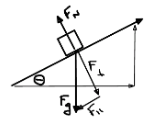
F_{perpendicular (⊥)}

= F_g cos()

F_{parallel (∥)}

=F_gsin()

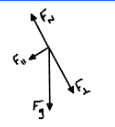
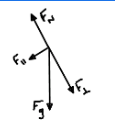
sum of forces (ΣF) in equilibrium

ΣF = 0N; the object is either stationary or moving at a constant velocity

Acceleration in equilibrium

a = 0m/s²; the object is either stationary or moving at a constant velocity

sum of forces (ΣF) in non-equilibrium

ΣF ≠ 0N; the object is accelerating or decelerating

acceleration in non-equilibrium

a ≠ 0m/s²; the object is accelerating or decelerating