Applied Linear algebra

Row Operations

The 3 elementary row operations:

1. Swap two rows.

2. Multiply a row by a nonzero scalar (e.g., divide a row by 3).

3. Add or subtract a multiple of one row to/from another.

Gaussian Elimination

Pivot Column

Pivot – first none zero in a row of matrix

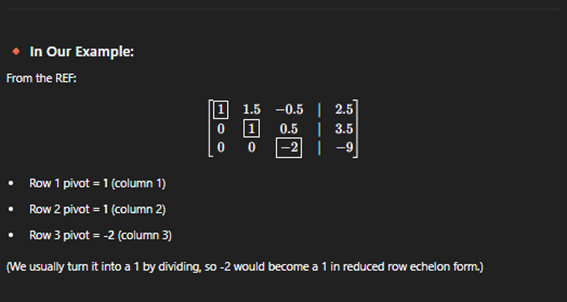
Row enchelon form

Row reduced enchelon form

Basically the difference between this and other, is the leading entry 1 has to be the only none zero in its columnt.first none zero in each row has to be 1

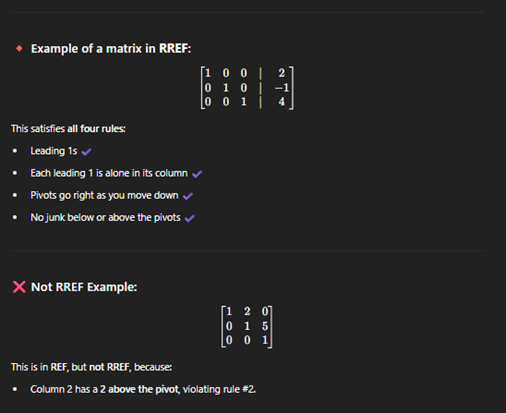
Pivot position and pivot column (Has to be be in row encholen form)

Basic and free variables

Basic variable – if it corresponds to a pivot column

Free variable -  if does Not correspond to a pivot column

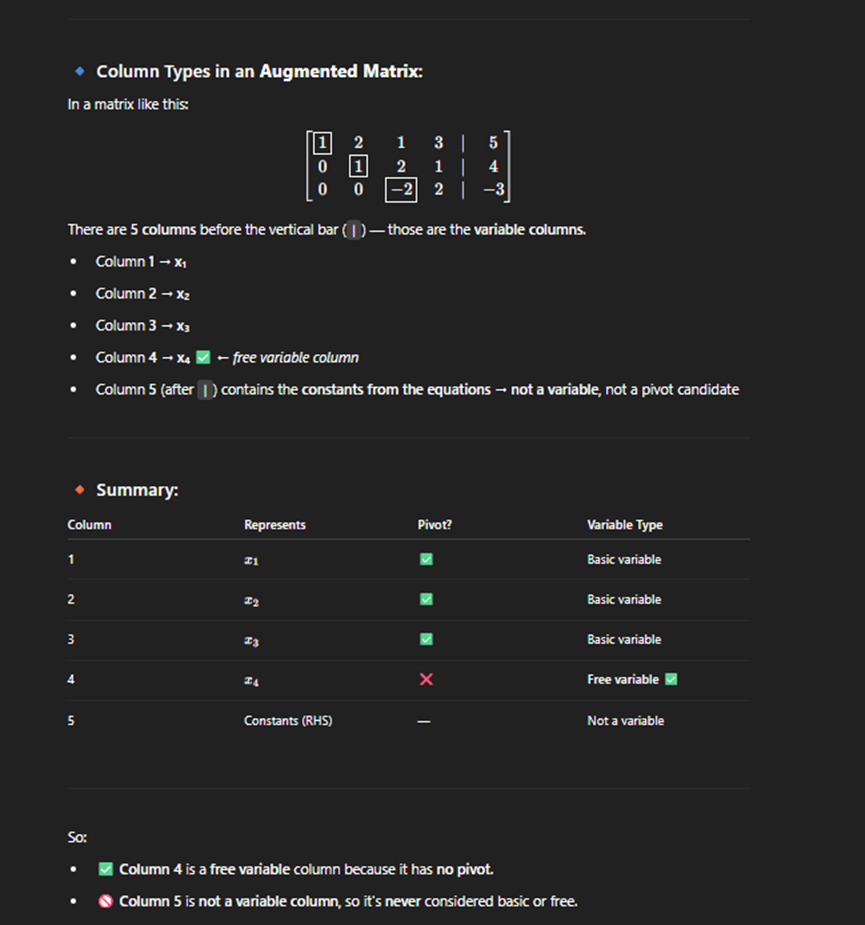
Consisent system

·         A consistent matrix is an augmented matrix that represents a system of equations with at least one solution.

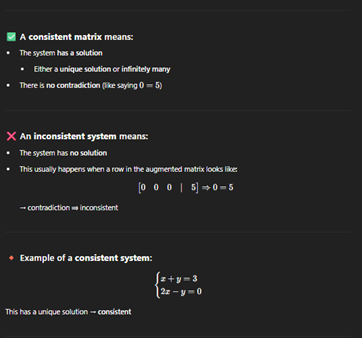
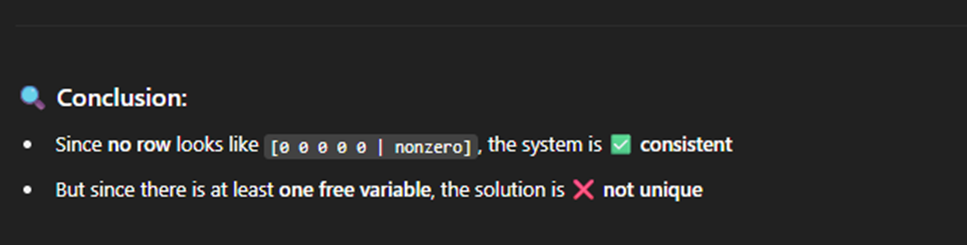
·         Unique no Free variables, no contradictions

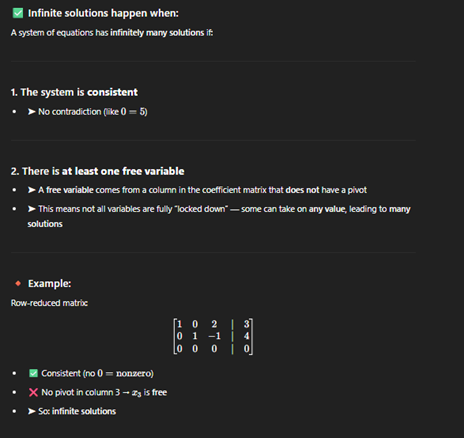
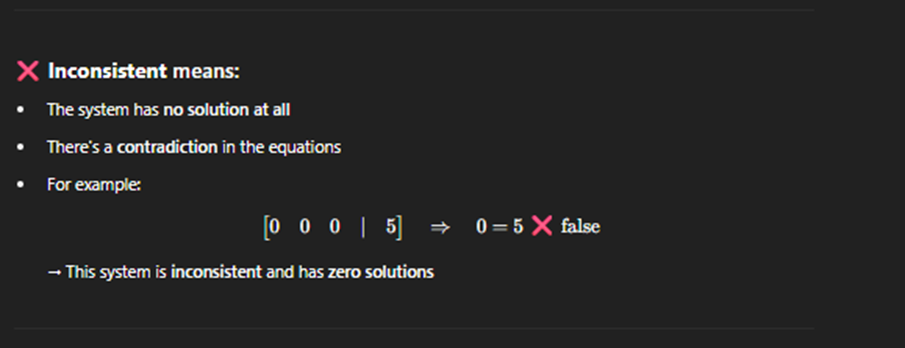
Rank

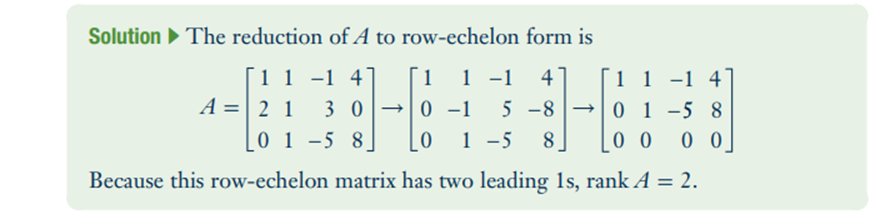
The number of pivot columns (i.e., the number of leading 1s) in its row echelon form

Homogeneous Equations

where all constant are 0.

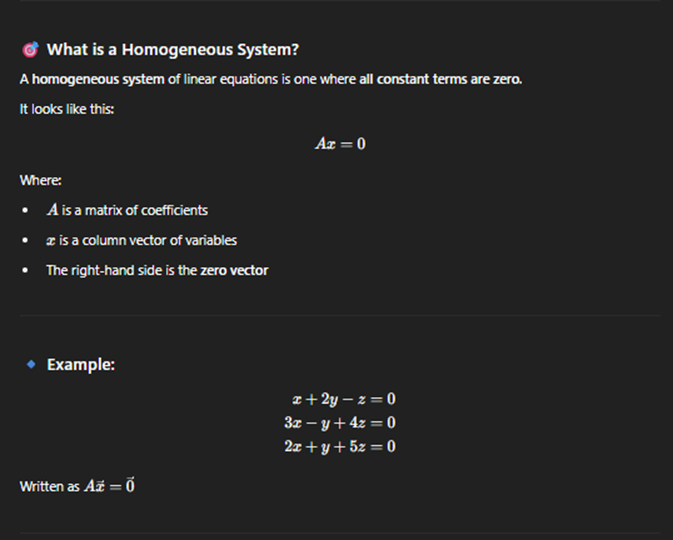
Homogeneous has at least one solution.

• If rank <n, then there are infinite solutions.

• If rank =n, then the only solution is the trivial one.

(n is the number of columns)

Trivial vs non trivial

Trivial if everything is 0.

Non trivial not 0.

Non trivial if there are any free variables

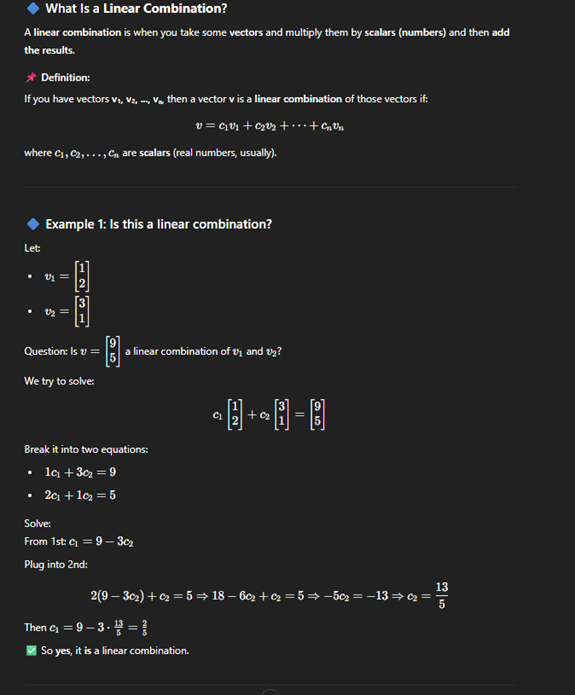
Linear Combinations and Basic Solutions

Matrix Addition

Has to be same size to add and minus

Scalar multiplication matrices

Vector Matrix Multiplication

Multiplying matrices

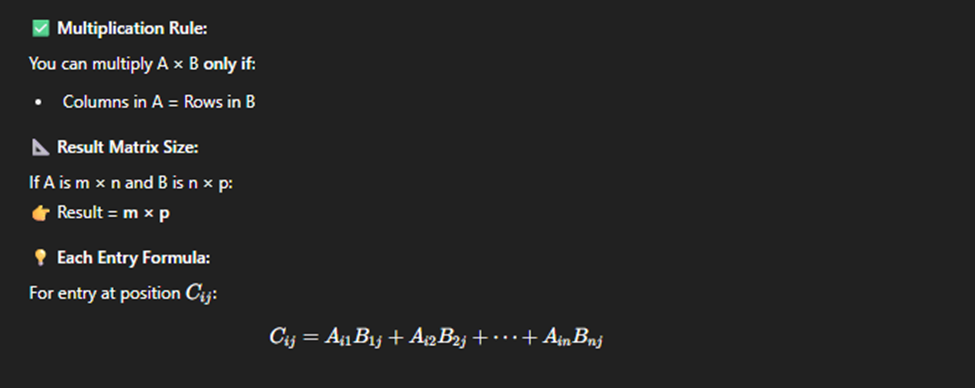
Transpose

Symmetric and skew symmetric

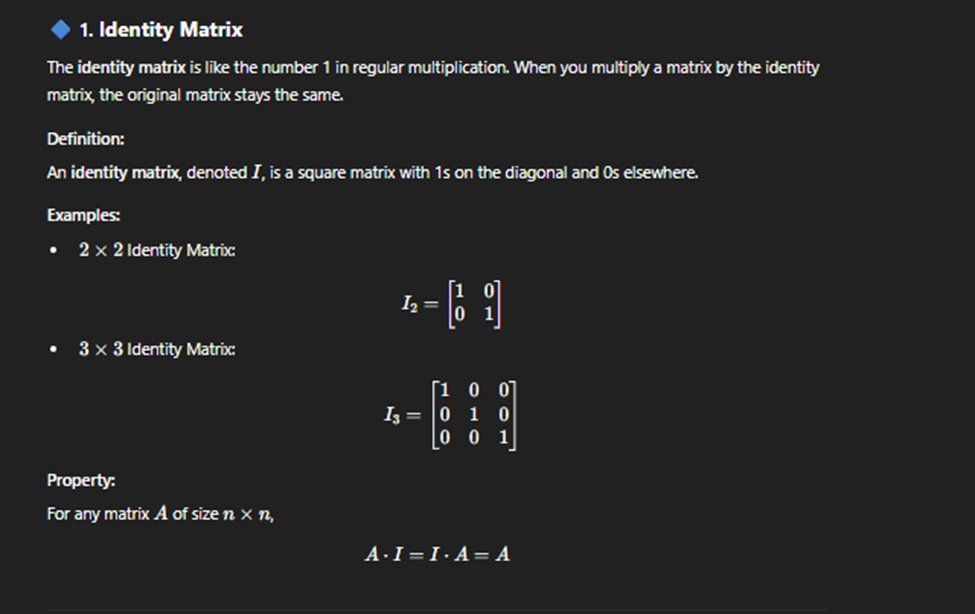
Identity matrix

Invertible matrix

Invertible matrices are basically matrices that have an inverse

Finding inverse of a matrix

A matrix with no inverse cannot get to this form (has to be reduced row enncholon form)

Solving linear system with matrices

Ax = B

(A^-1)Ax = (A^-1)B

x = (A^-1)B

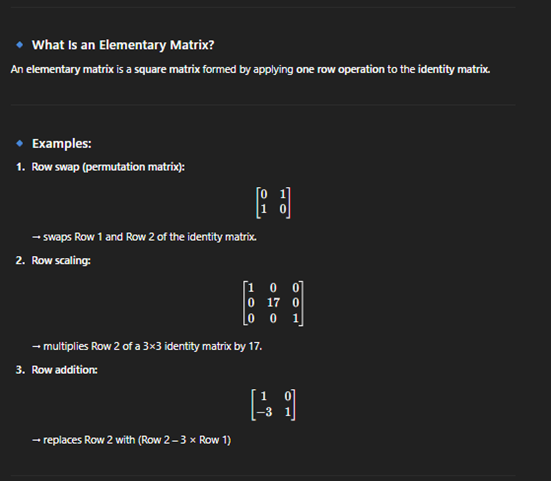
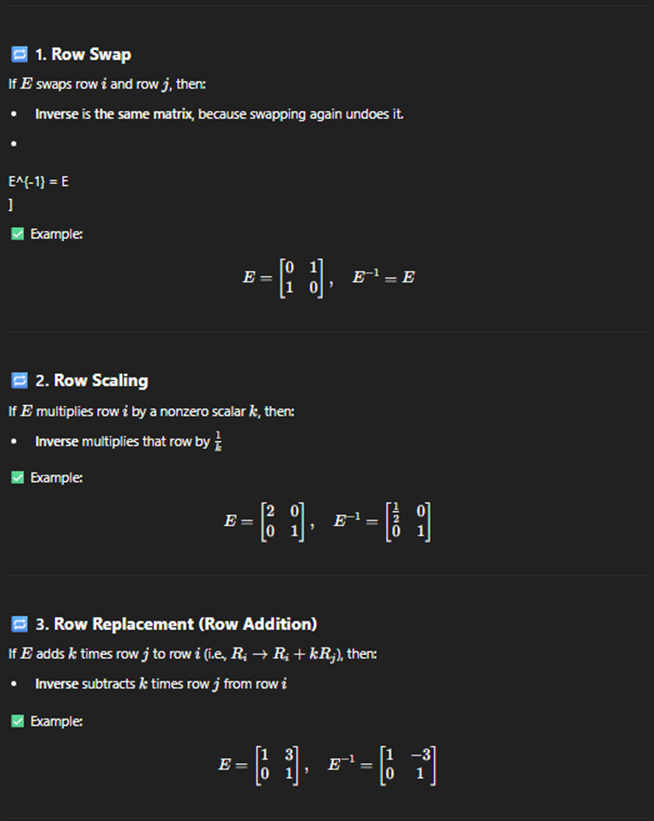
Elementary matrices

Inverse of elementary matrices

·         Every elementary matrices is invertible

·         An elementary matrix represents a single row operation done to an identity matrix. Its inverse is simply the matrix that undoes that operation.

Triangular matrices

·         A triangular matrix is a square matrix (same number of rows and columns) where all entries on one side of the main diagonal are zero.

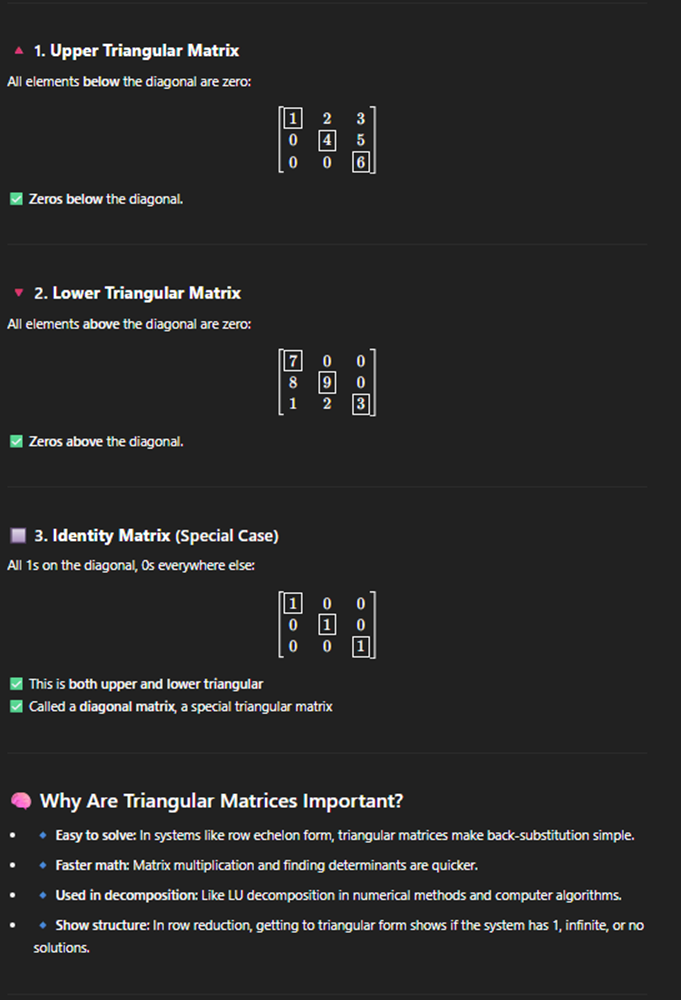
Determinant

single number calulated from a square matrix (2×2)(3×3)(….)

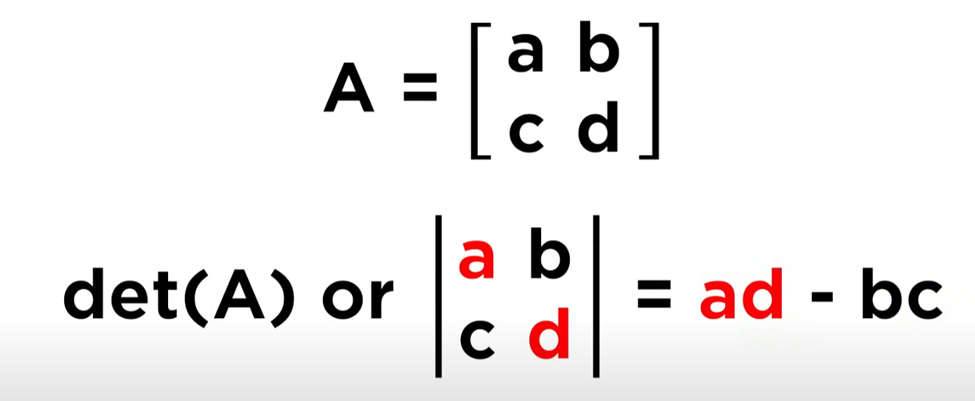
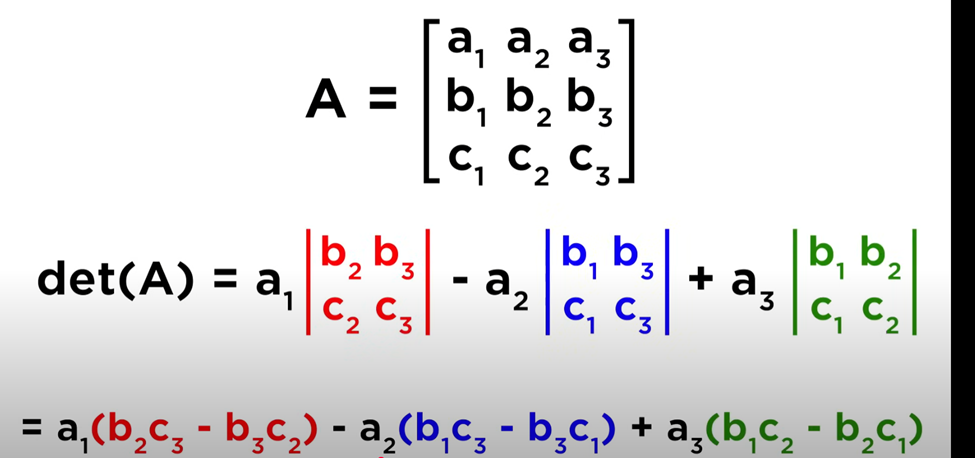
Matrix minros

·         Basically doing the determinate at that point we are looking at for minors

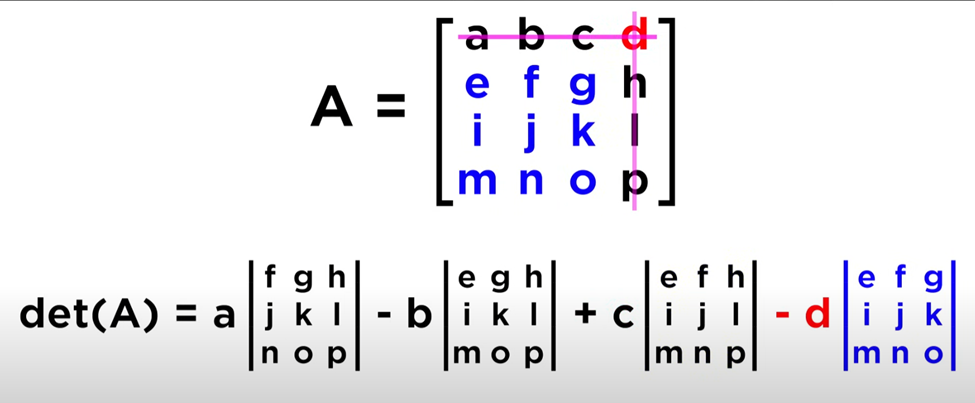
Cofactors

Determinant cofactor expansion

(can choose a row or column)

Determinant triangular matrix

Properties of determinants

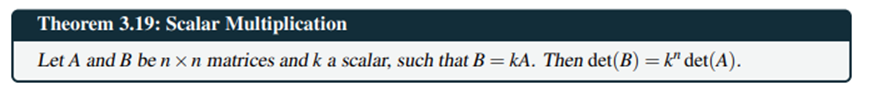
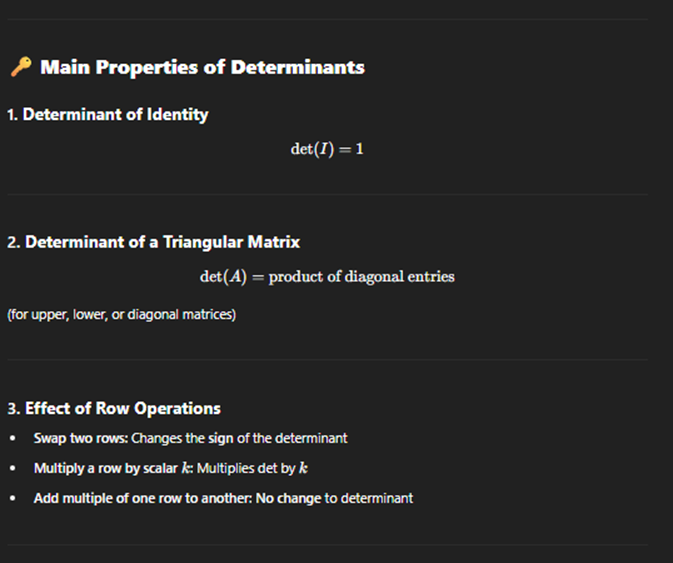
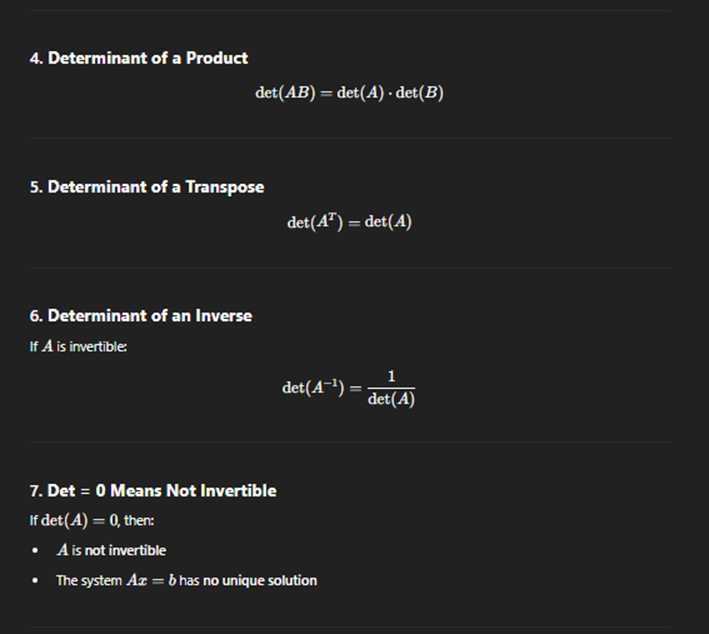
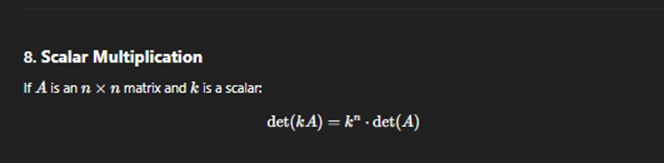
Determinant usign row operations

·         Make matrix into a triangular matrix

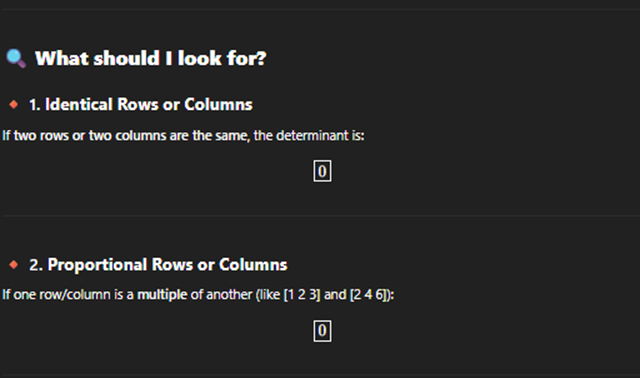
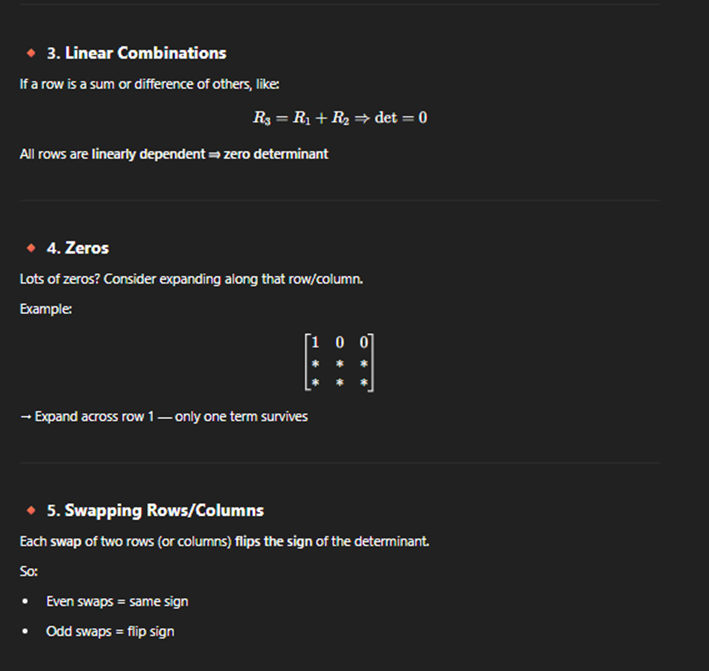
Determinant cursory inspection

·         Cursory inspection means evaluating a determinant quickly by observing special patterns or properties — without full cofactor expansion or row reduction.

·         It saves time, especially on multiple choice tests or when recognizing zero determinants.

Vector formula

Position Vector

Properteis of Vector

Vector Linear combination

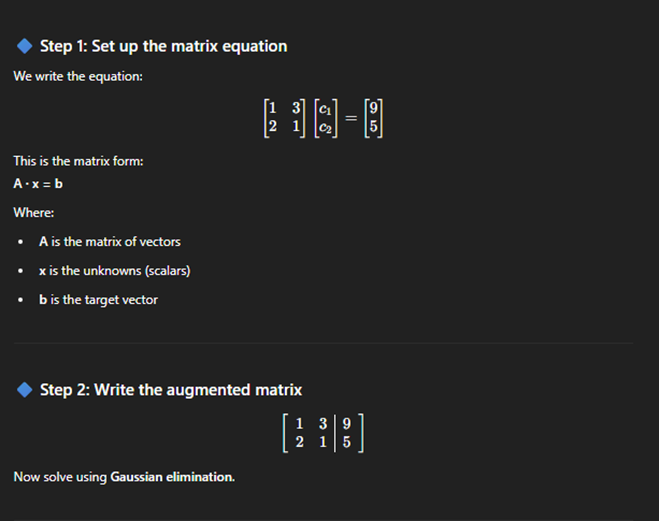
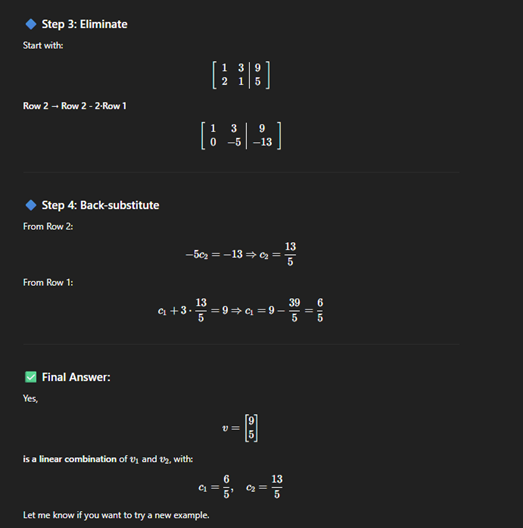
Distance between points

Length and Unit vector

Dot product

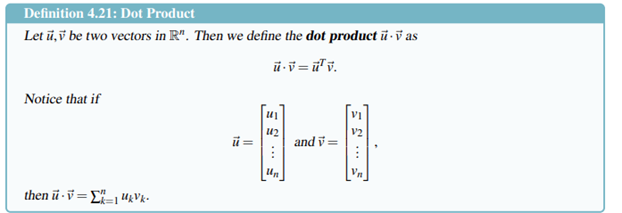
if dot product 0 means hey are perpendicular(othrogonal)( right angle) to each other

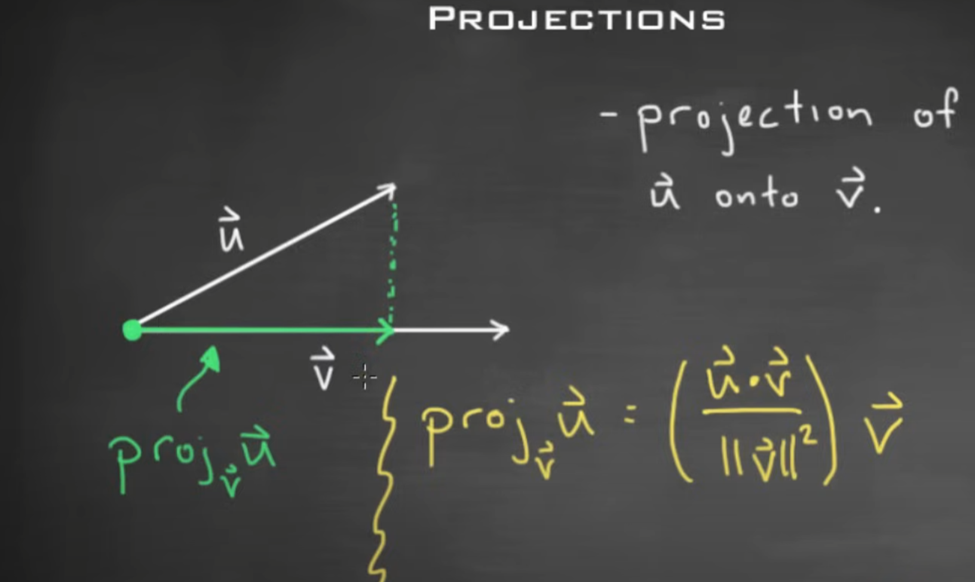
Projection vector

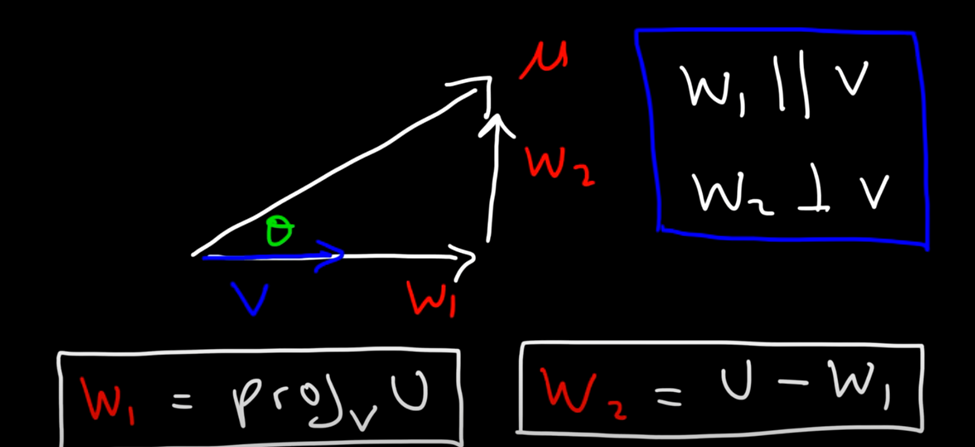
w1, and w2 are components of Vector U

w1 is projection of vector U onto vector V(thats how its described)(component of Vector U that is parralel to vector V

w2 is teh component of vector U that is othorgonal to vector V

Projection tells you how far one vector goes in the direction of another vector.

Why we use projection: 1. Shortest distance to a line or plane

Want to know the closest point on a line to a point? Use projection.
→ You find where the "shadow" of the point lands on the line.

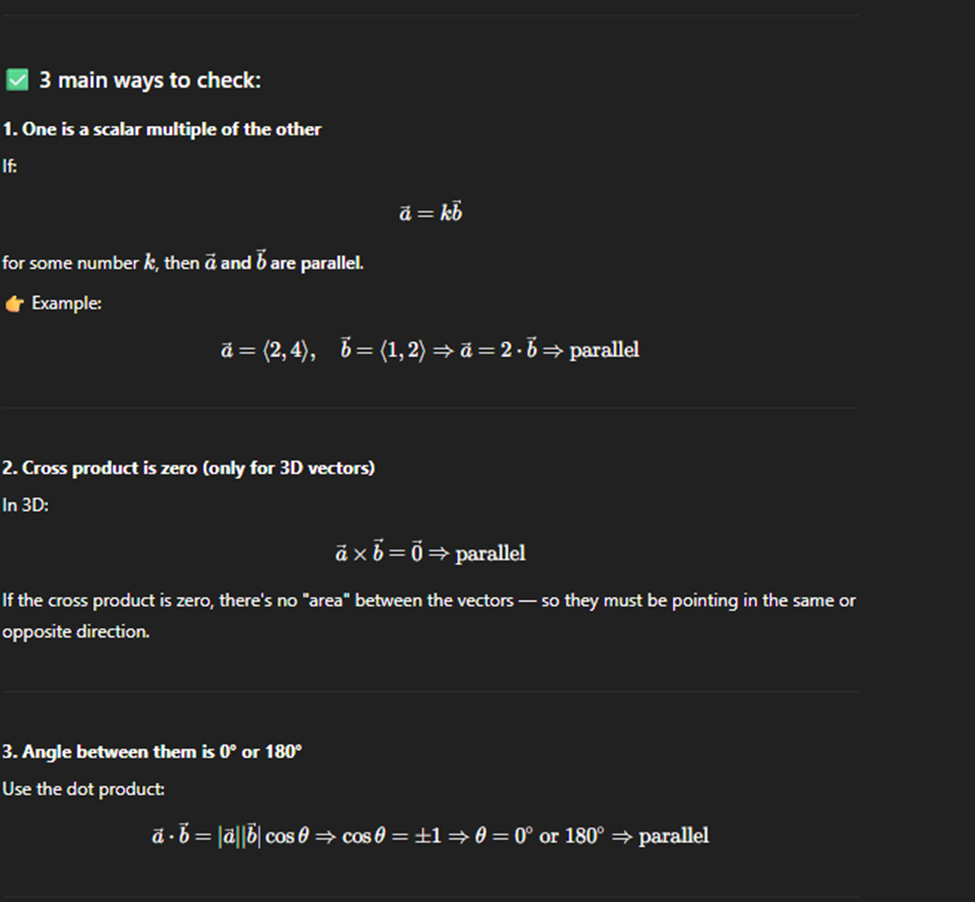
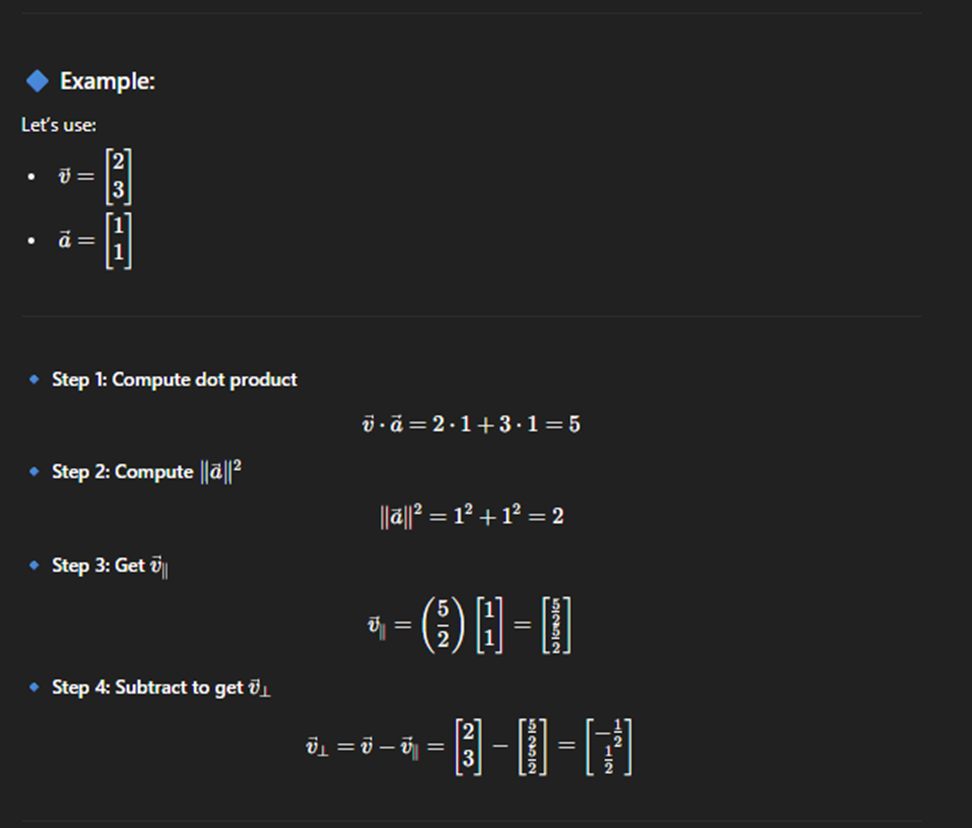
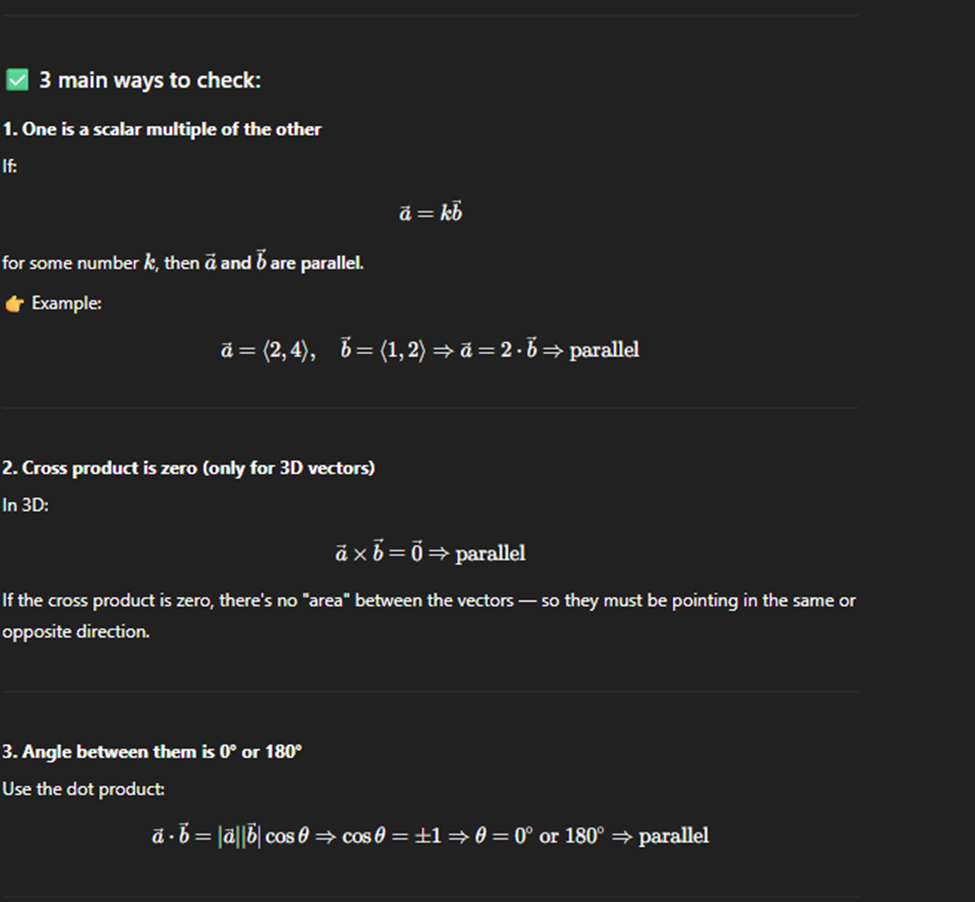
Parallel and perpendicular vectors

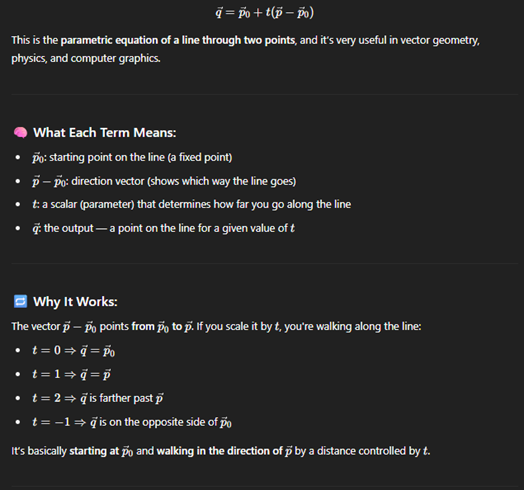
Paremetic lines

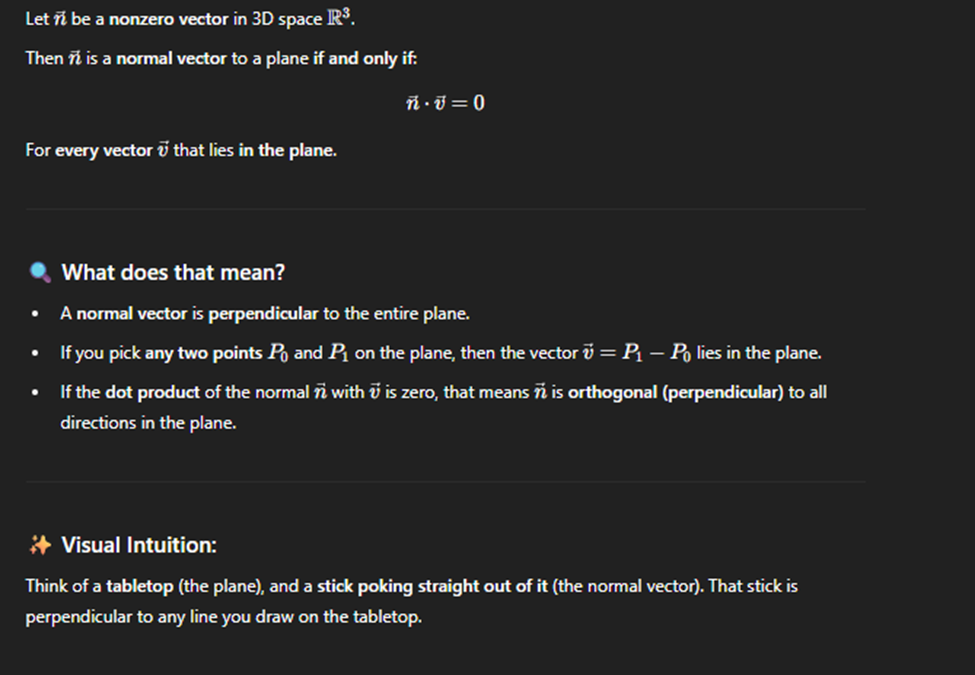
Plane Normal vector and Vector equation

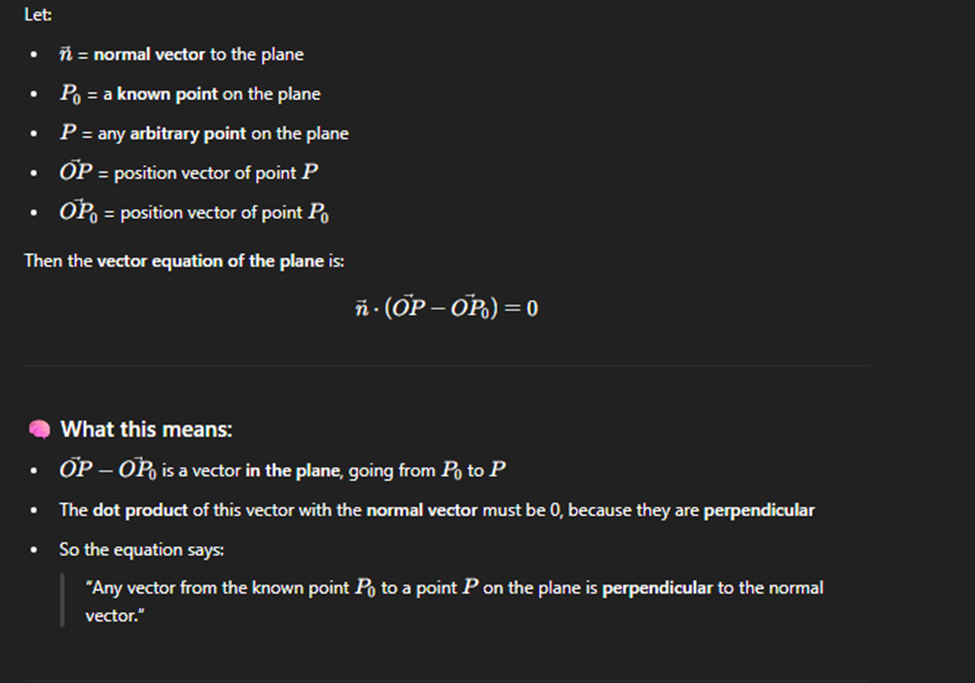
so if we get 0 then it means that P is a point on the plane

Scalar equation of a plane in R3

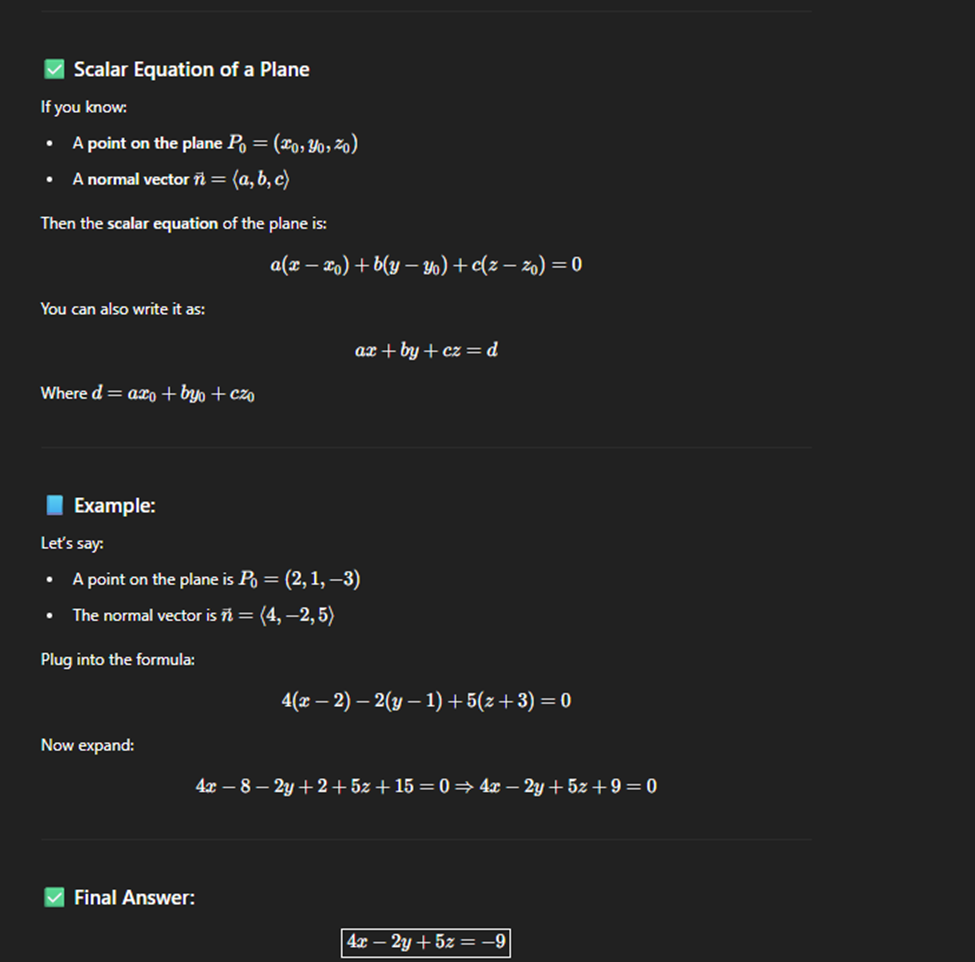
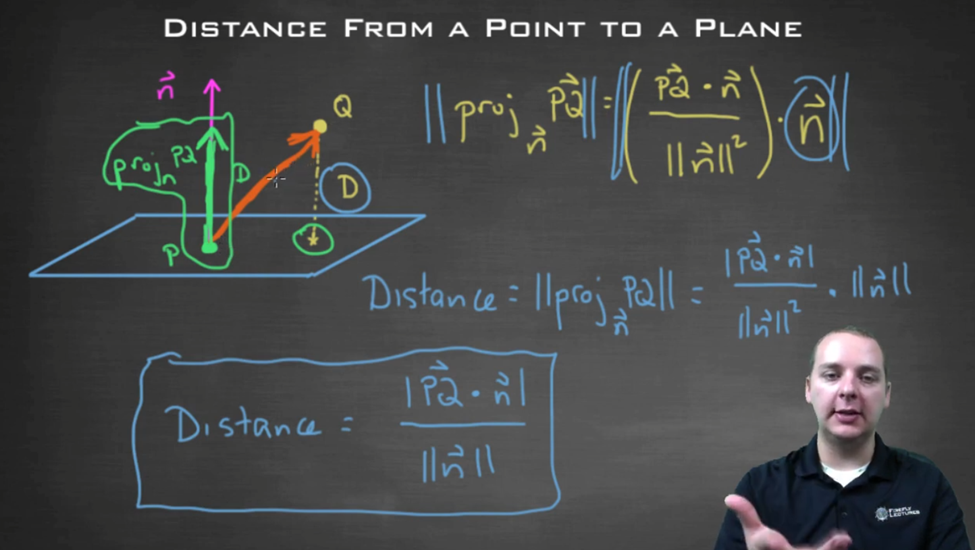
Find equation of a plane

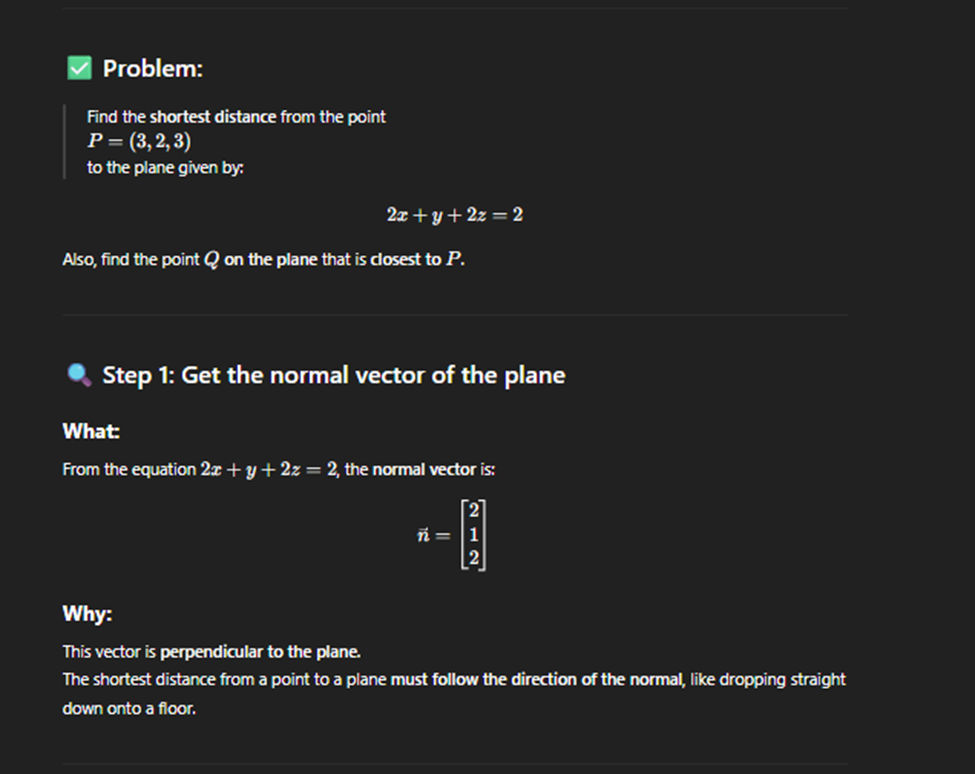
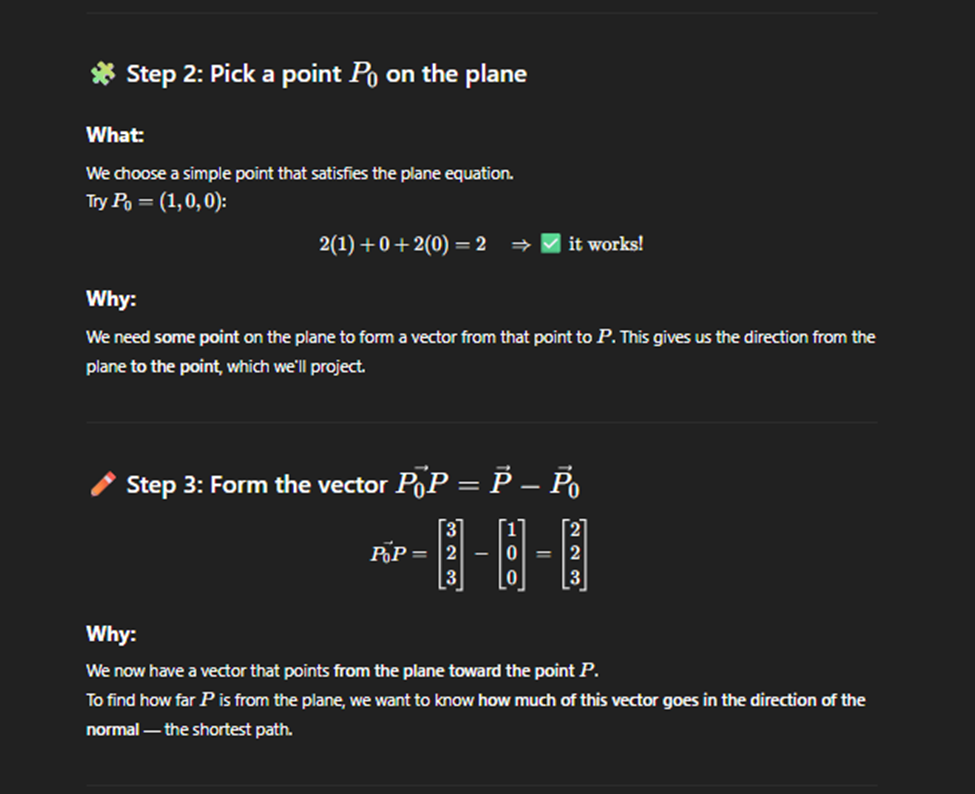
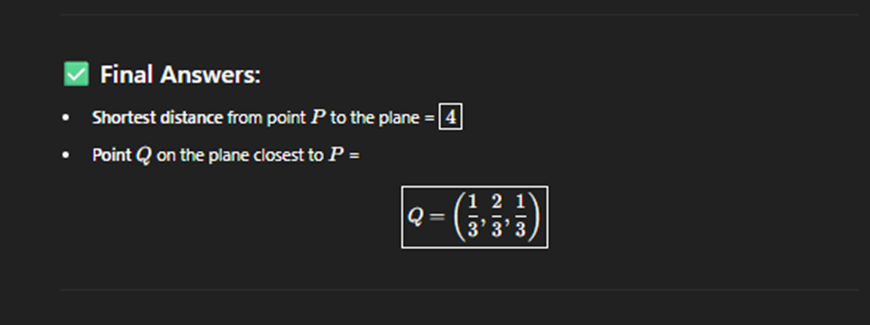
Span of vectors

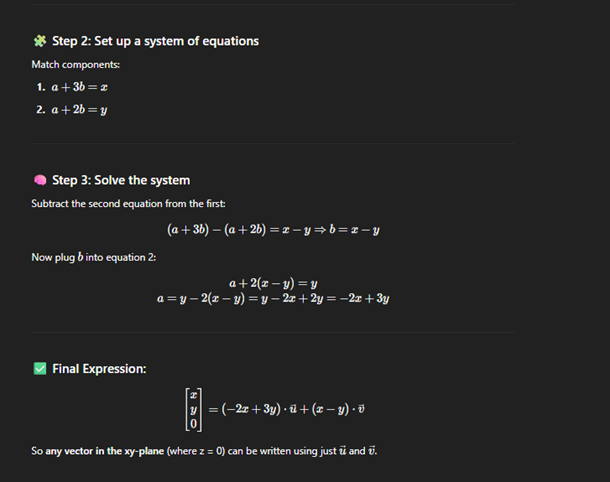
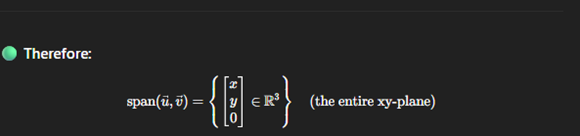
Describe vectors minum span

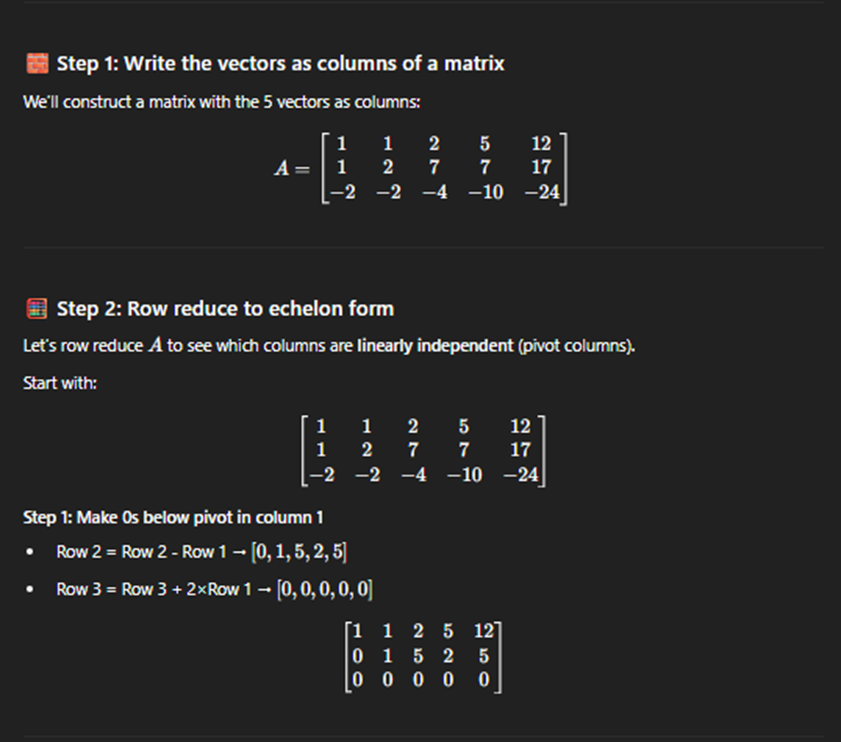
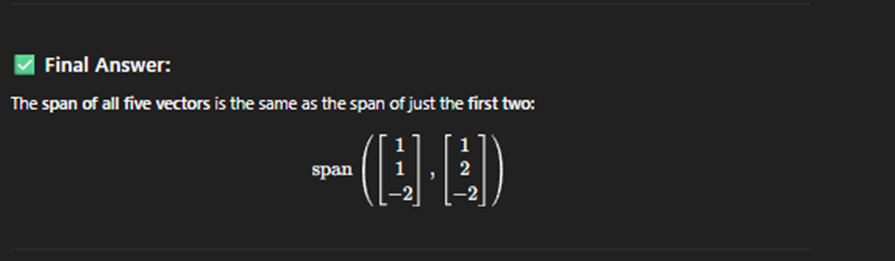
Solvign linear indpenetn

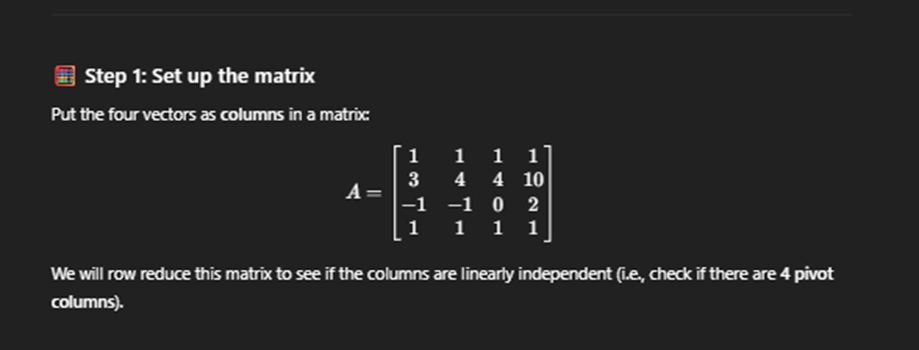
Vectors in a span

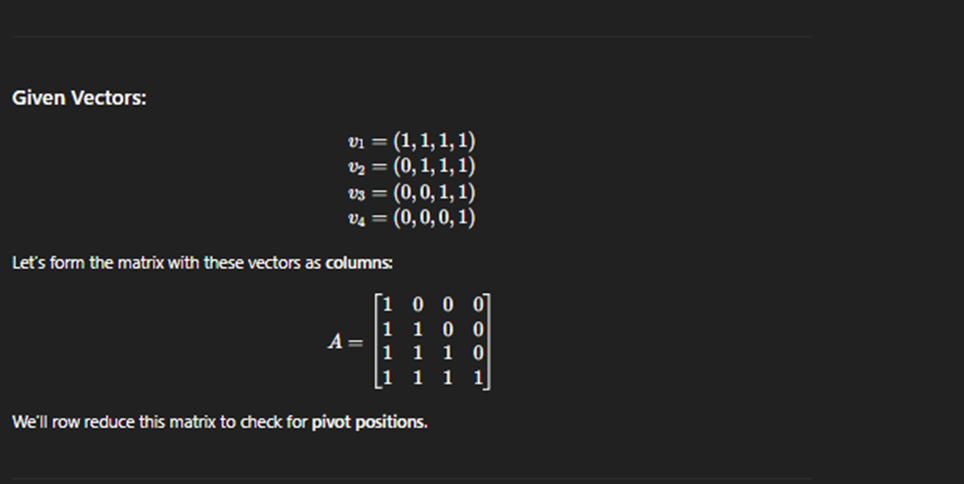
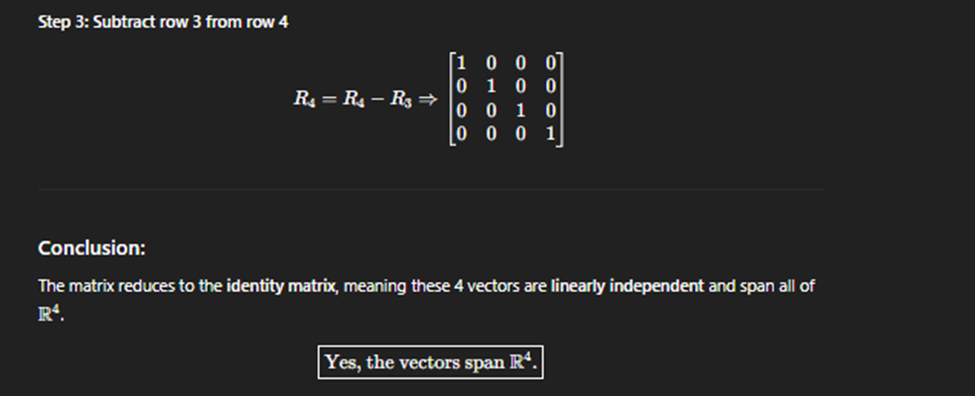
if linearly indpenedent then spans all of

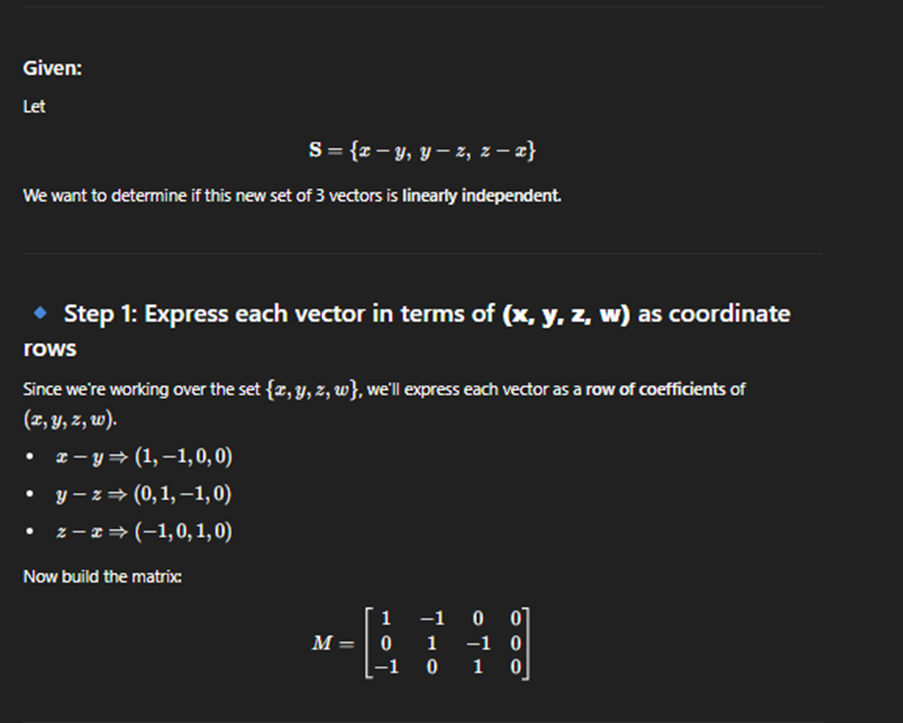
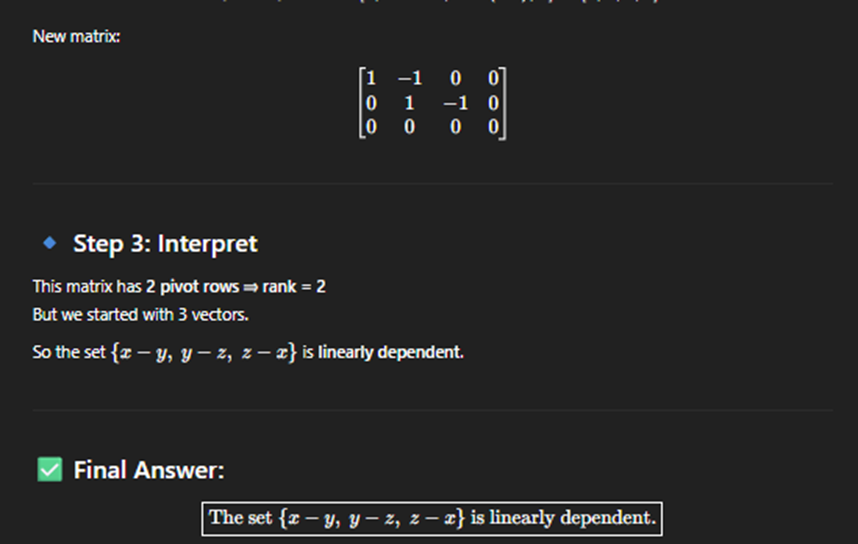
Linearly Dependent

ANY COLUMN LACKS pivot then its a linearly Dependet

Linearnily Indpendent

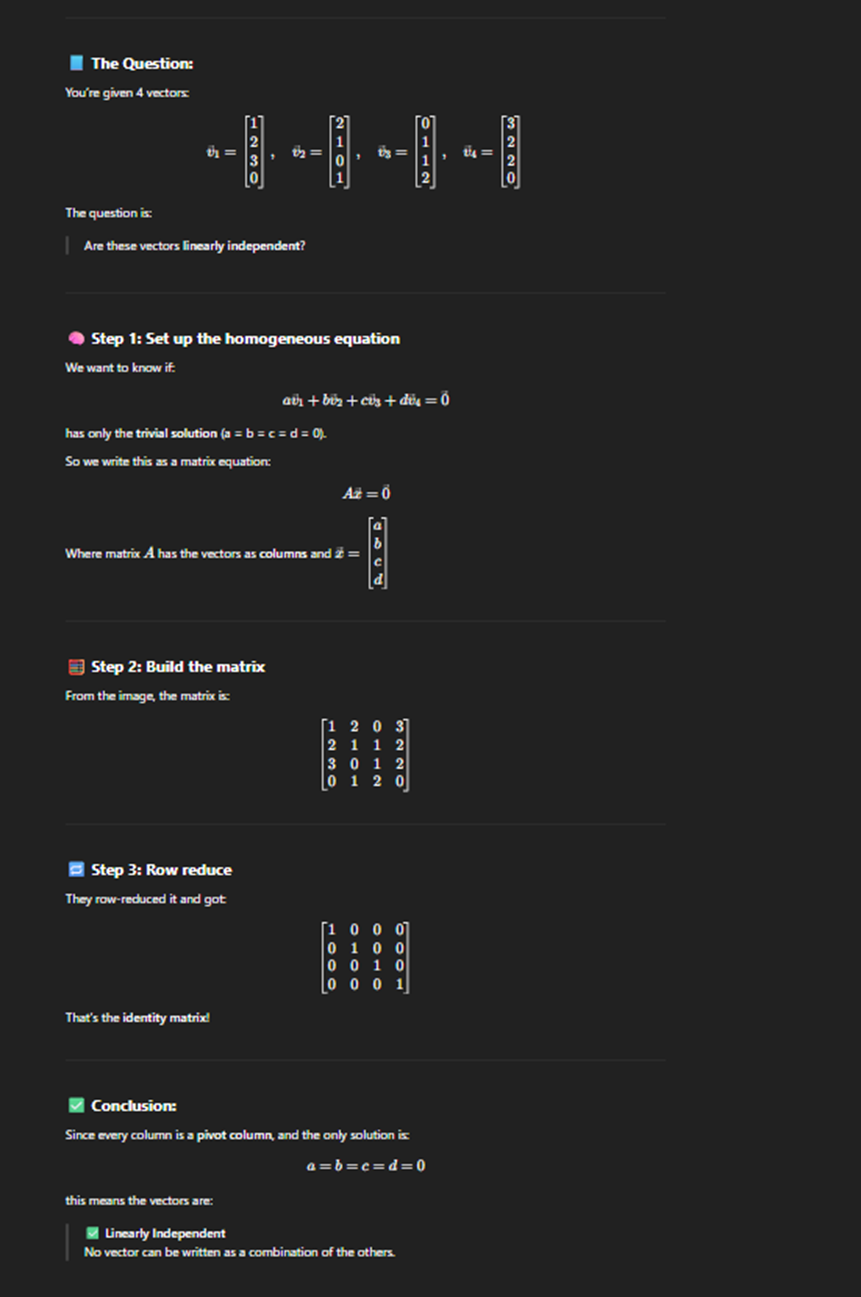
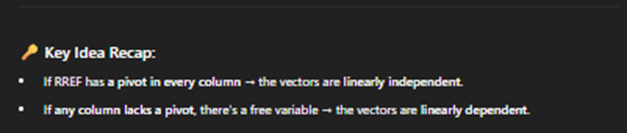
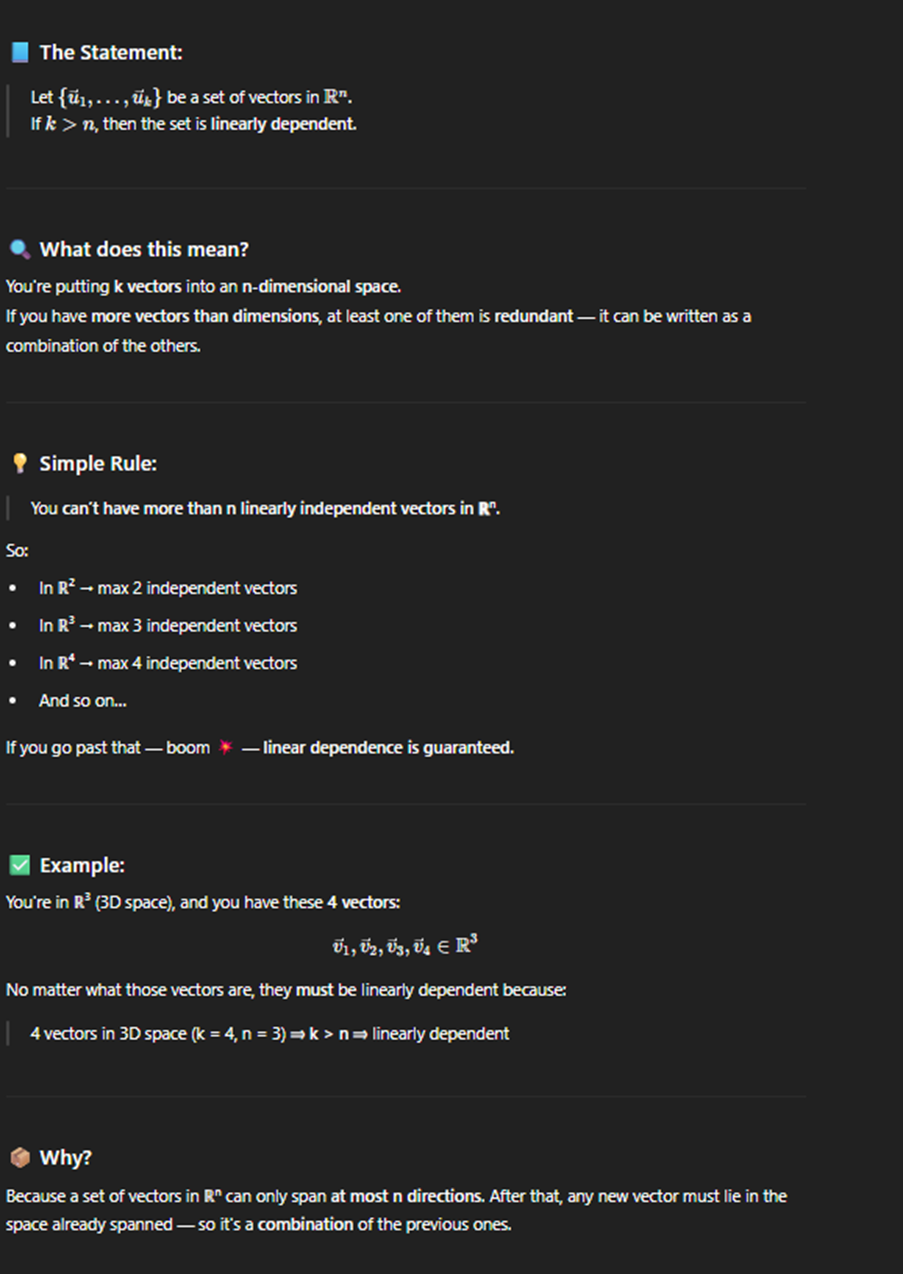
Rule for linearly indpendent or Dependent on span

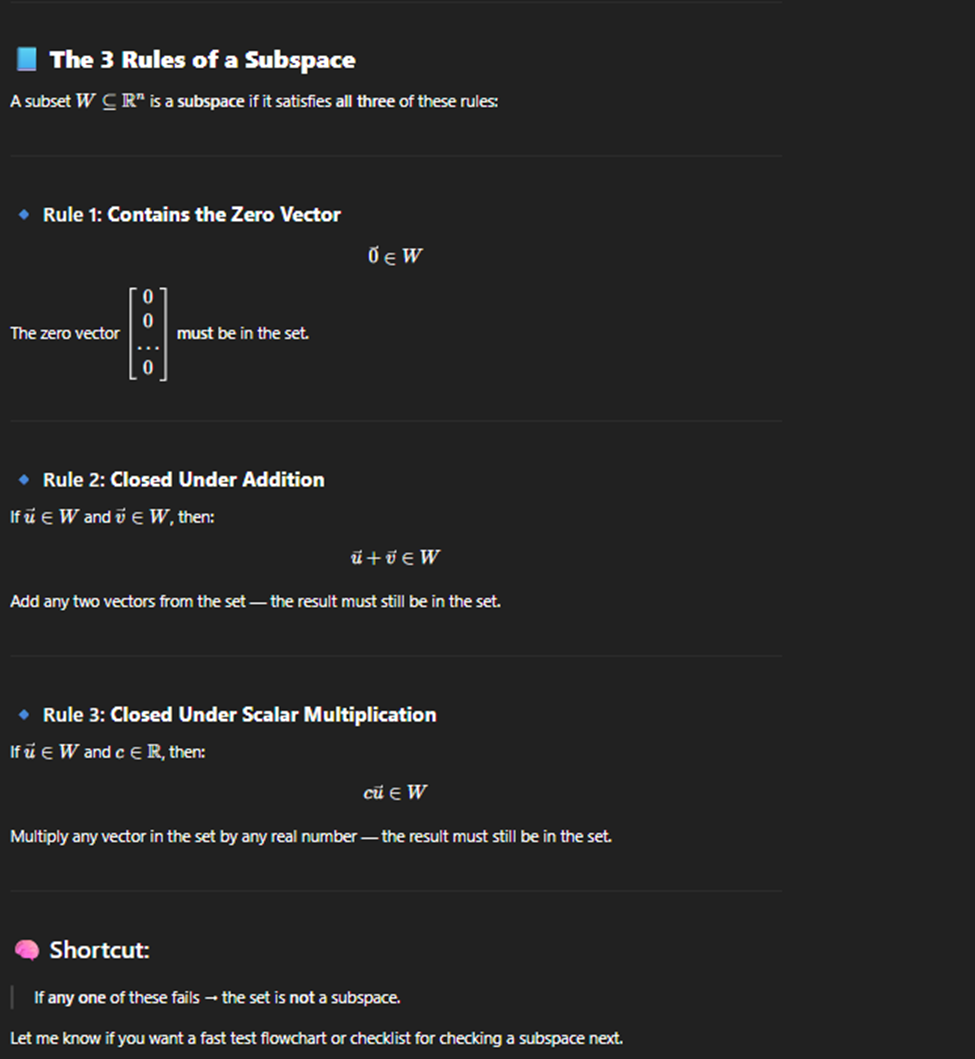
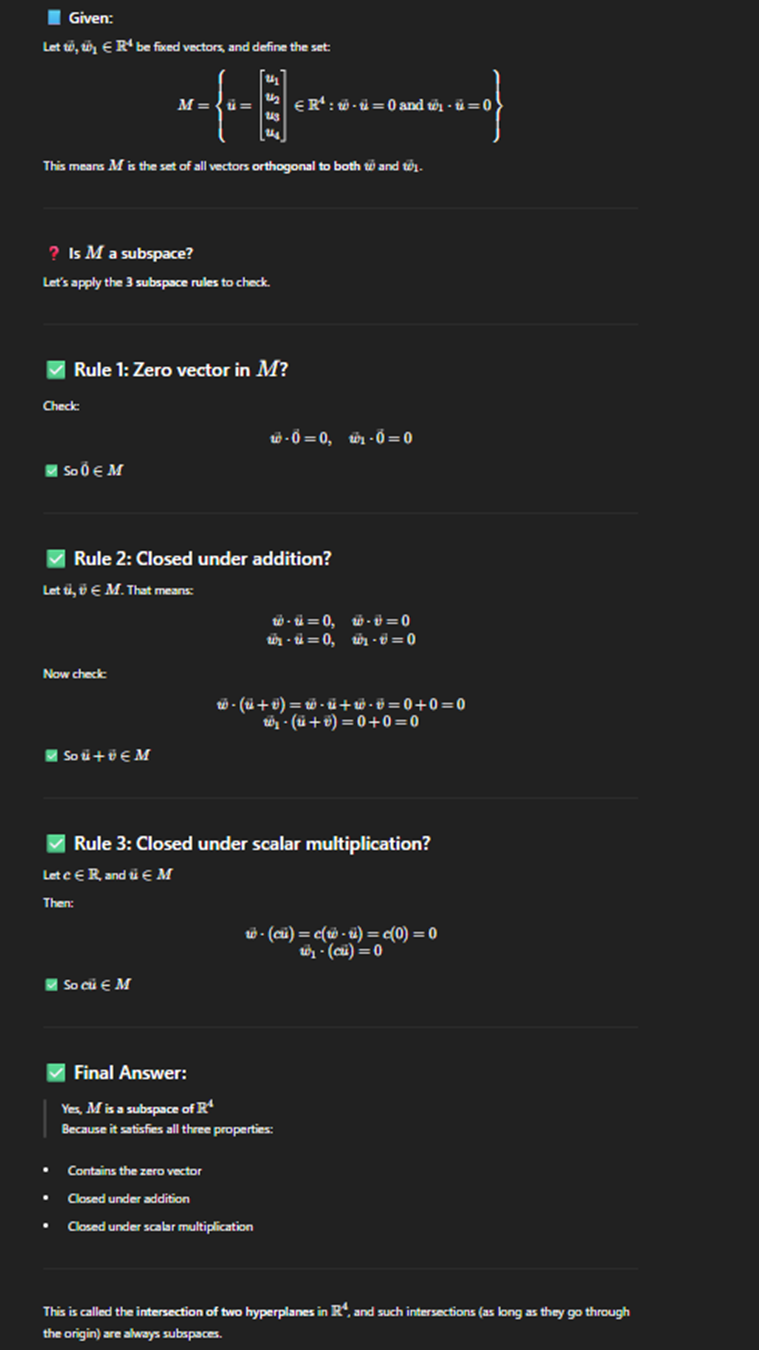
Subspace

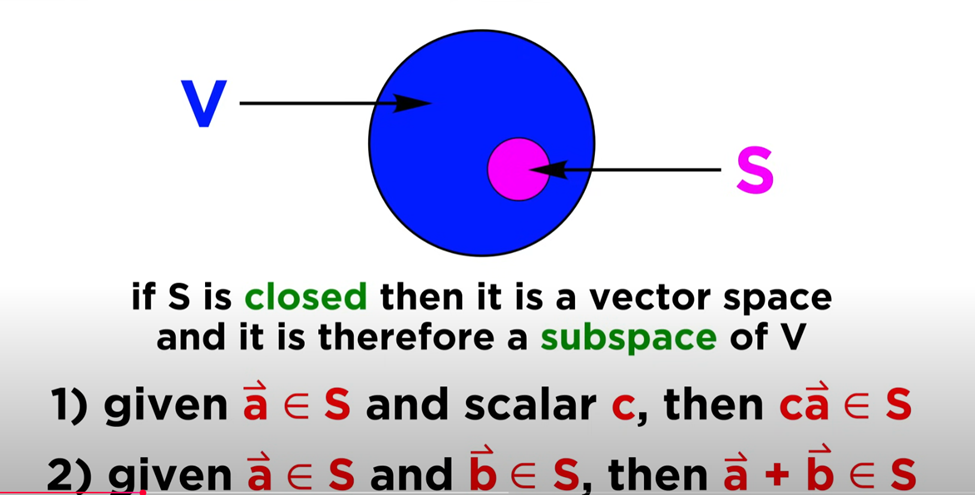
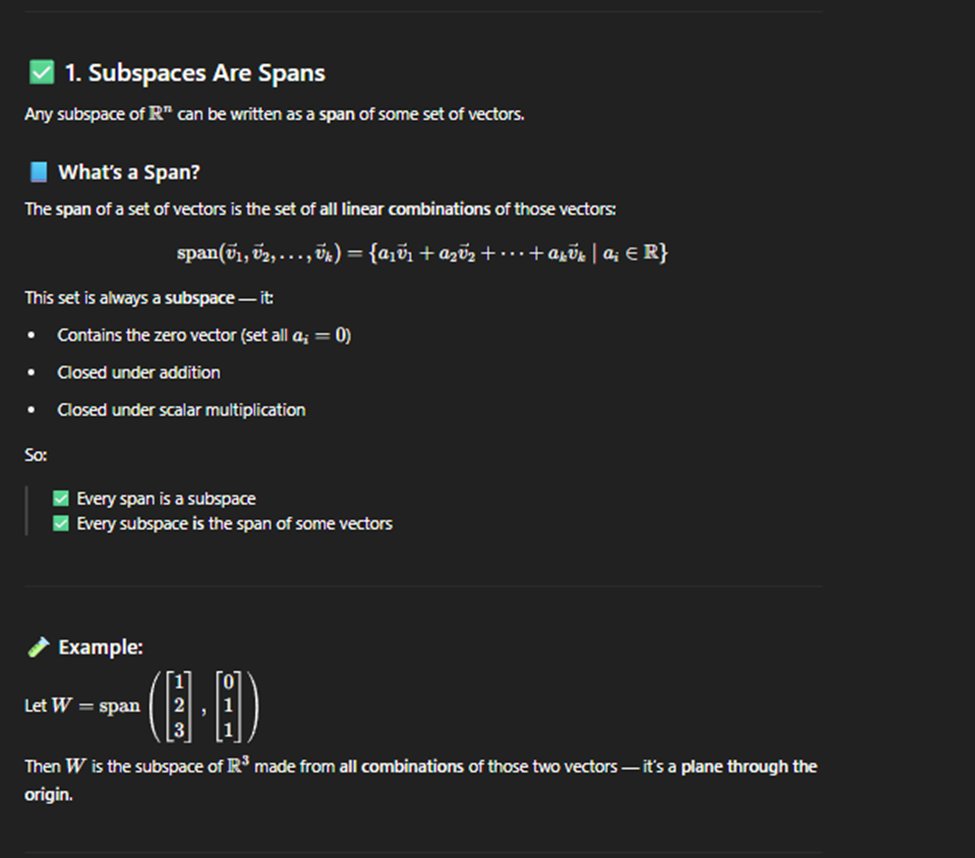
Subspace are spans

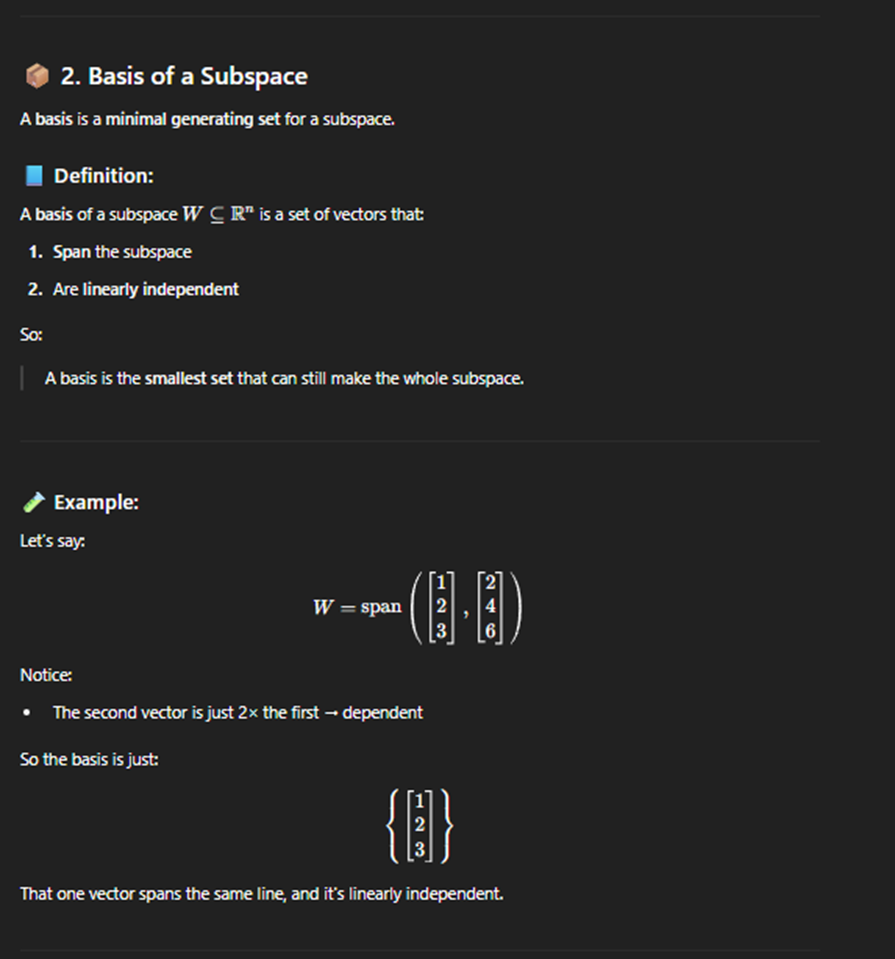
Dimention of a subspace

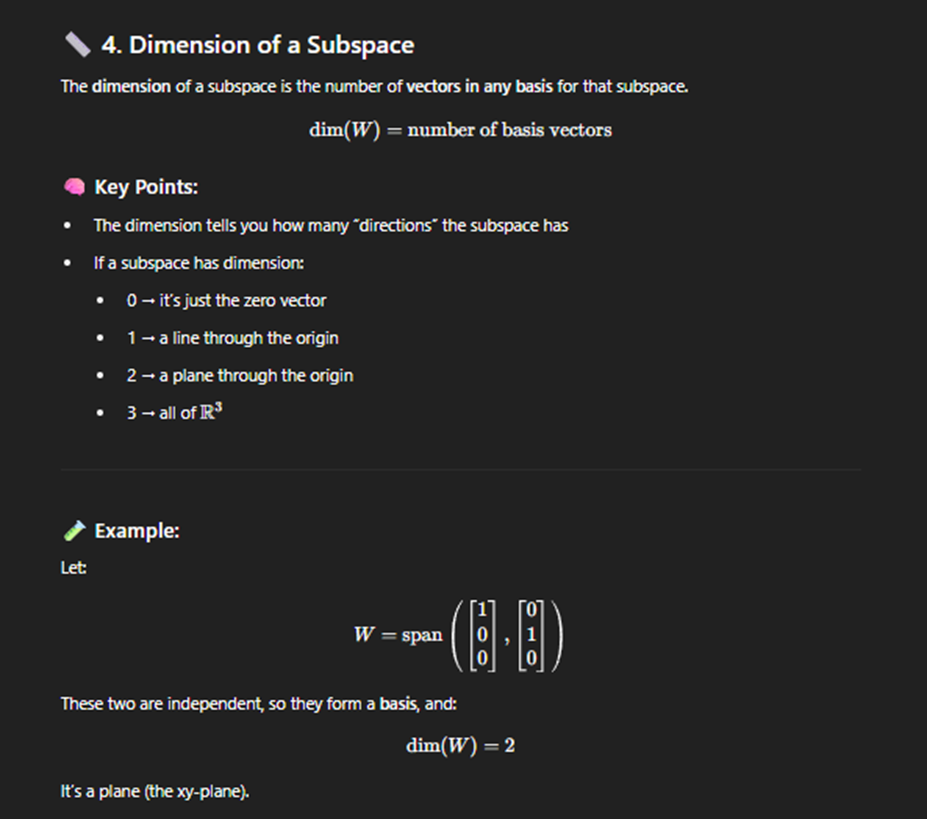
Findind dimension of Subspace and basis

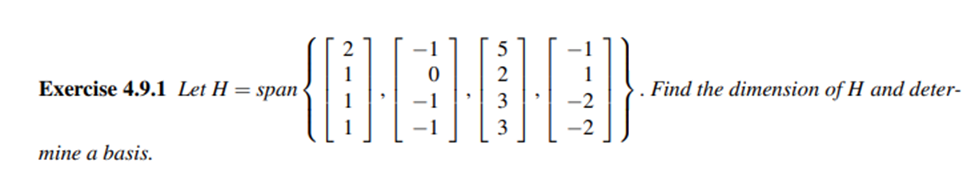
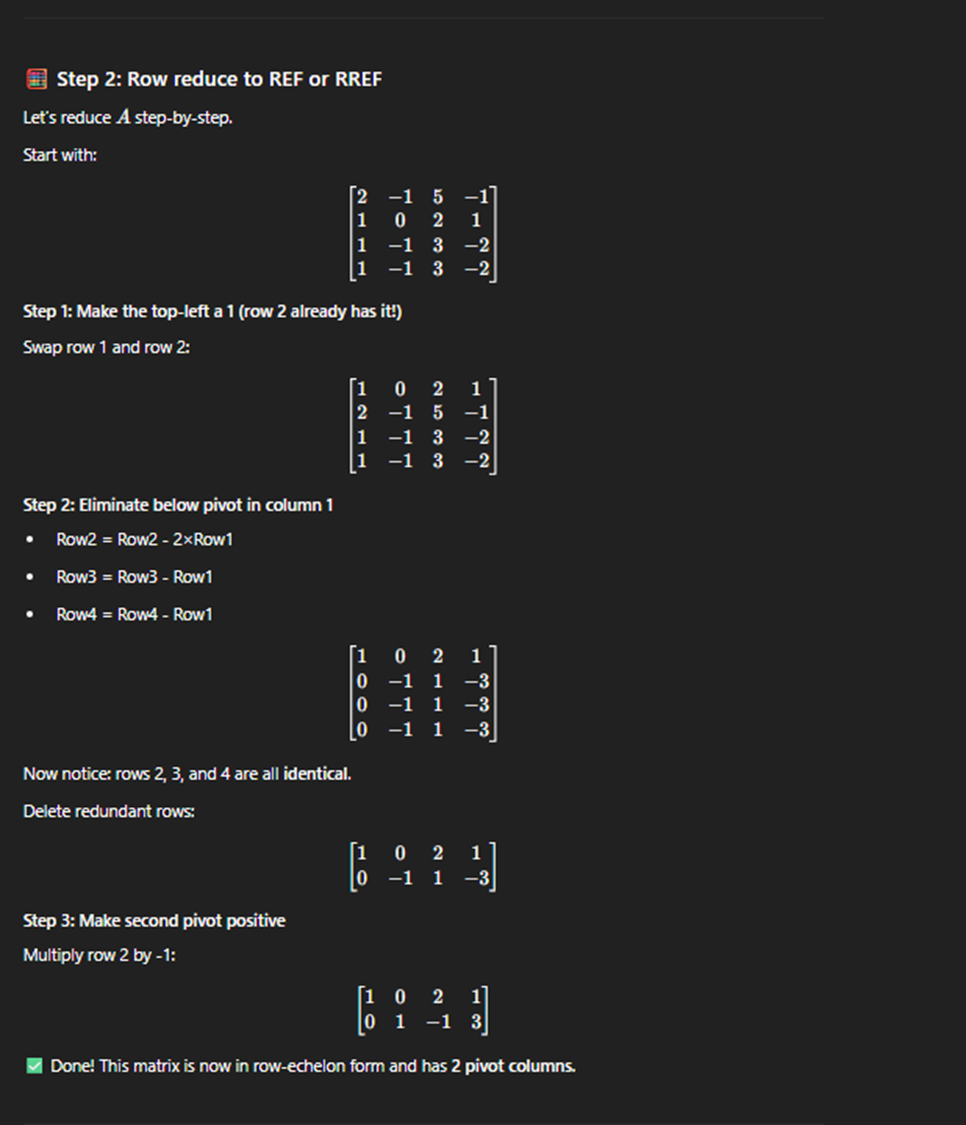
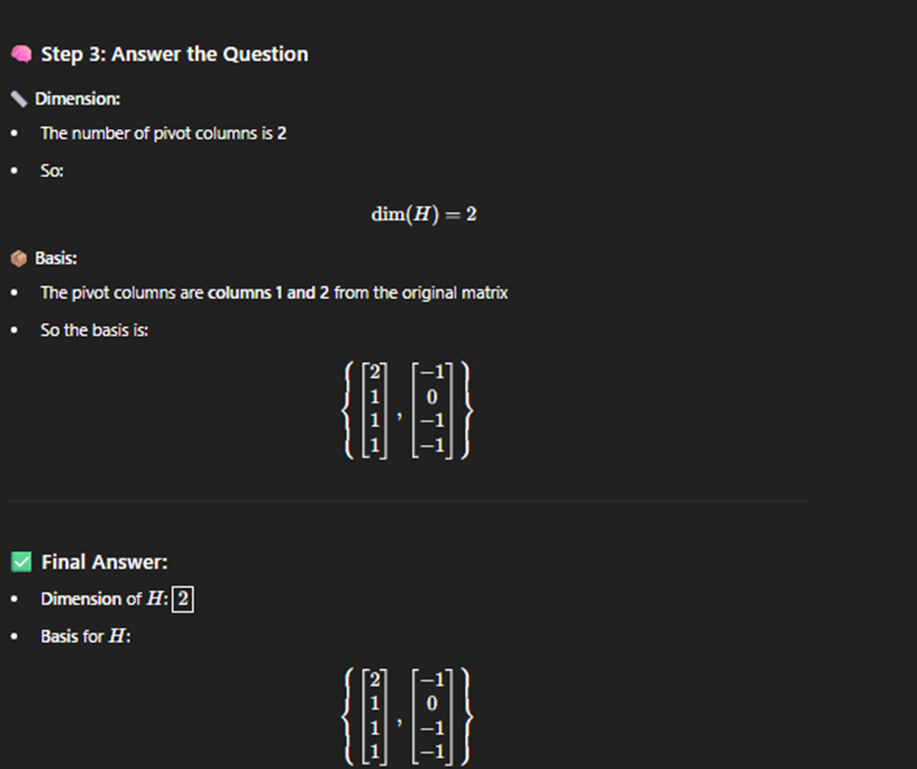
Solving subspace

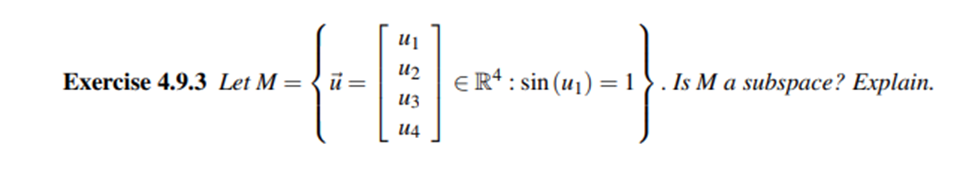
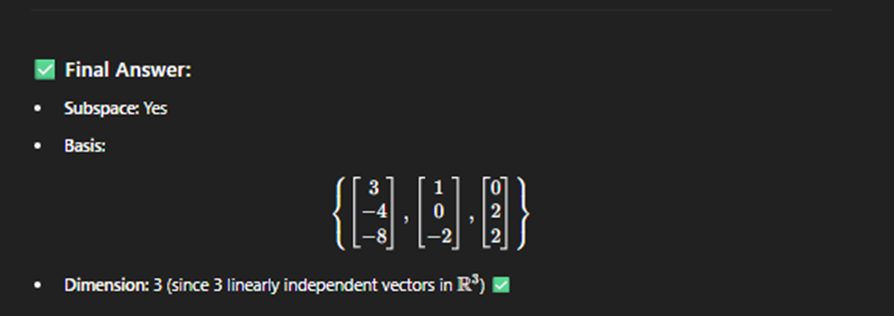
Solvign subspace 2 (remmerb is a supspace then linearly indpendent)

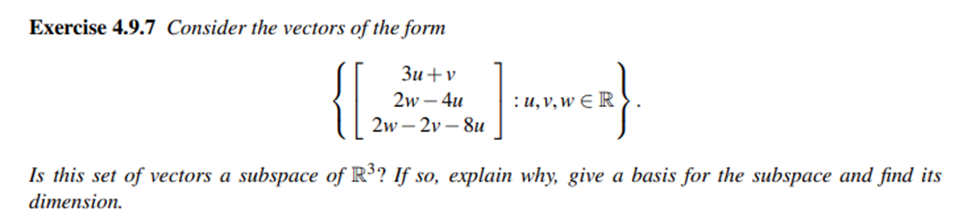
Rank of a matrix

Row Space

Any row that has a pivot colum is part of teh row space

Column space

Any column that has a pivot column is part of column space

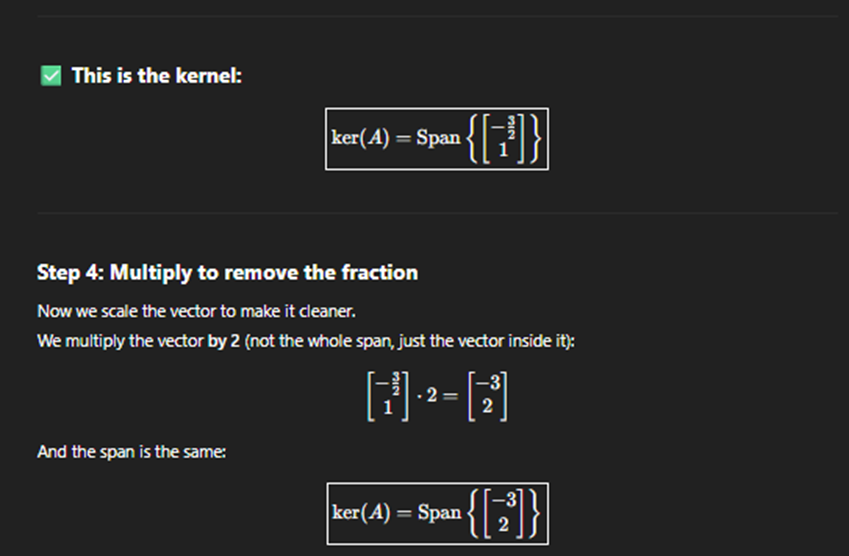
null space or kernal space

what multplied by A gives us 0

Rules of row space

rules for column space

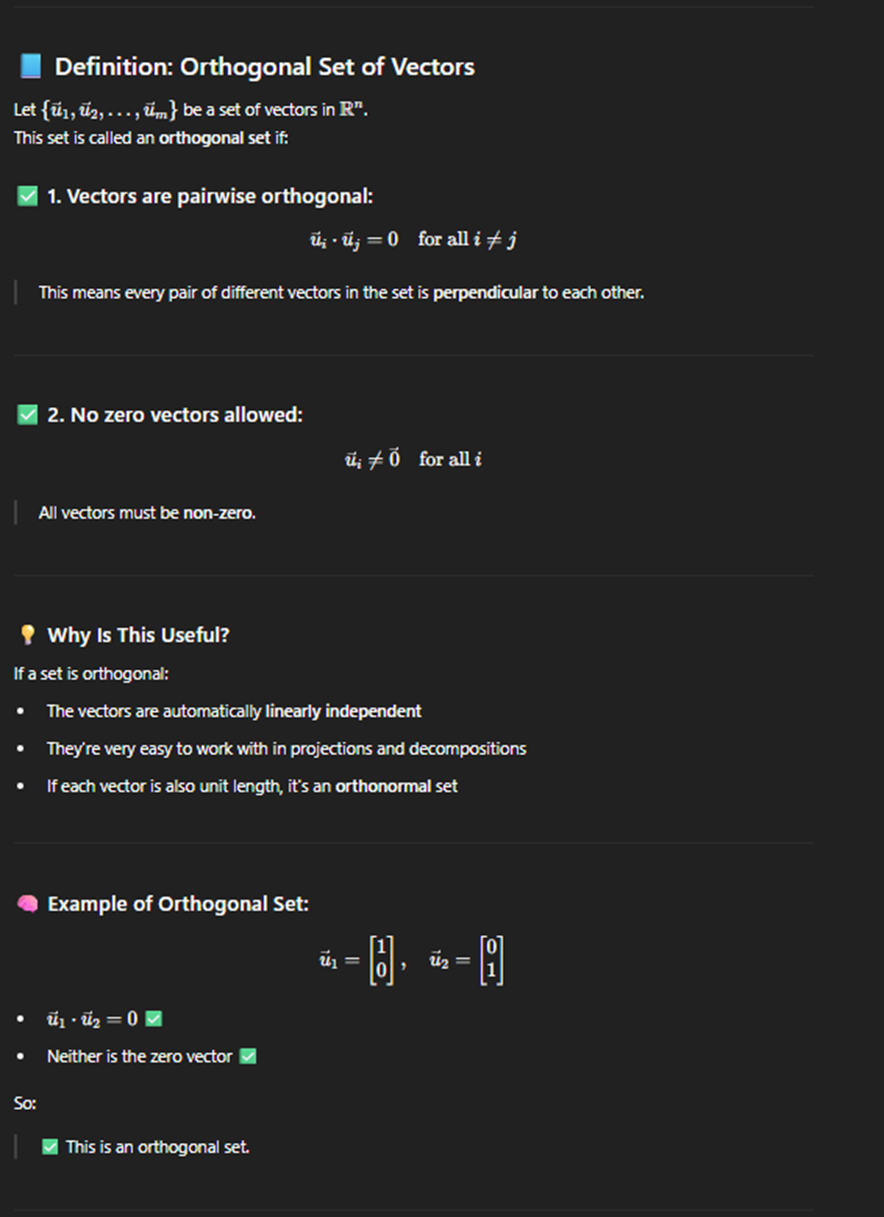
Orthogonal set

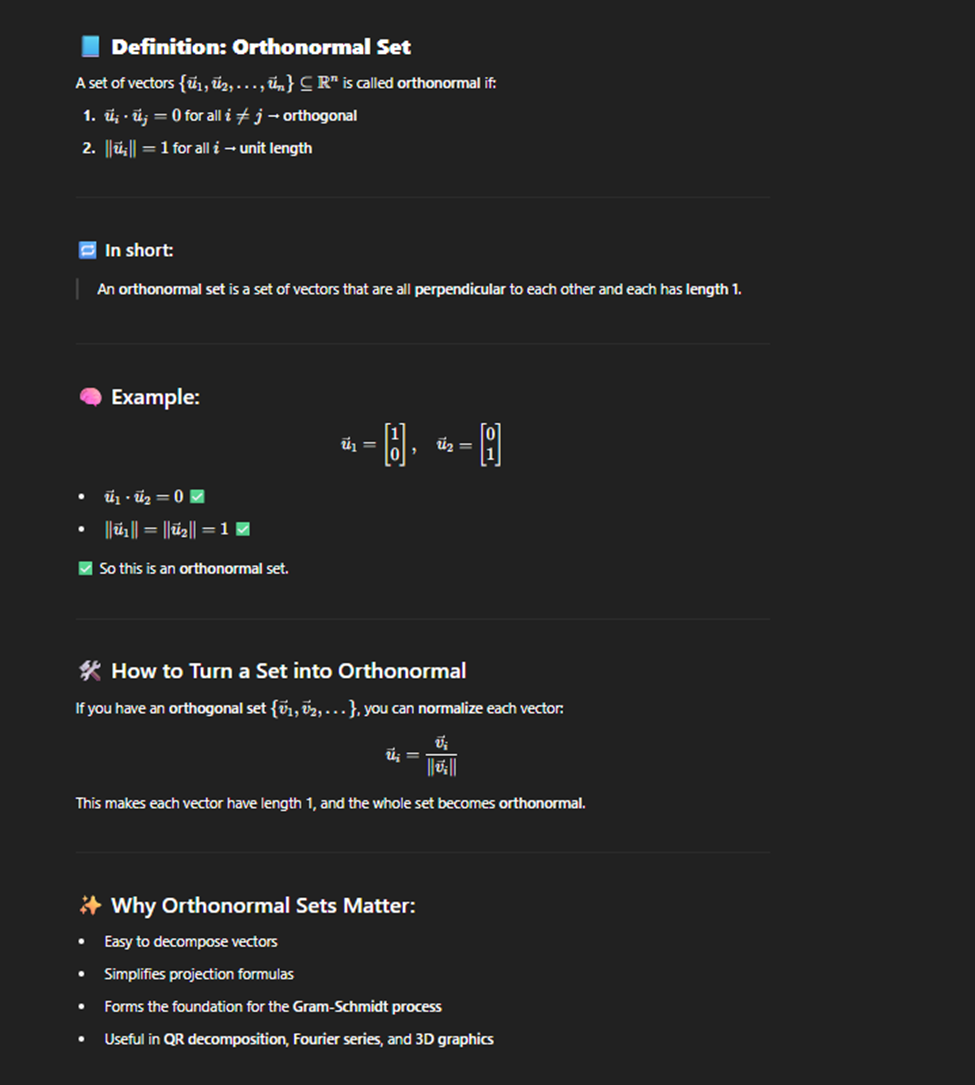
Orothornamal set

Fourier expansion

Orothogonal matrixes

Orthornamal basis

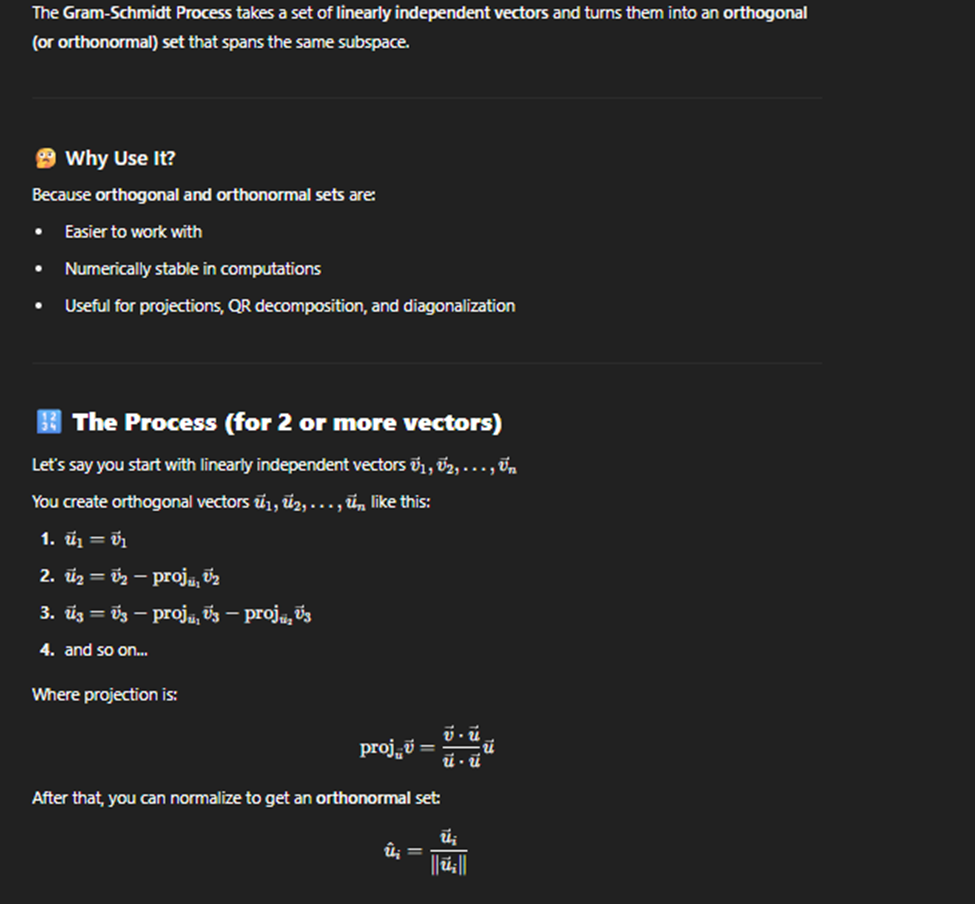
Grand smit processs

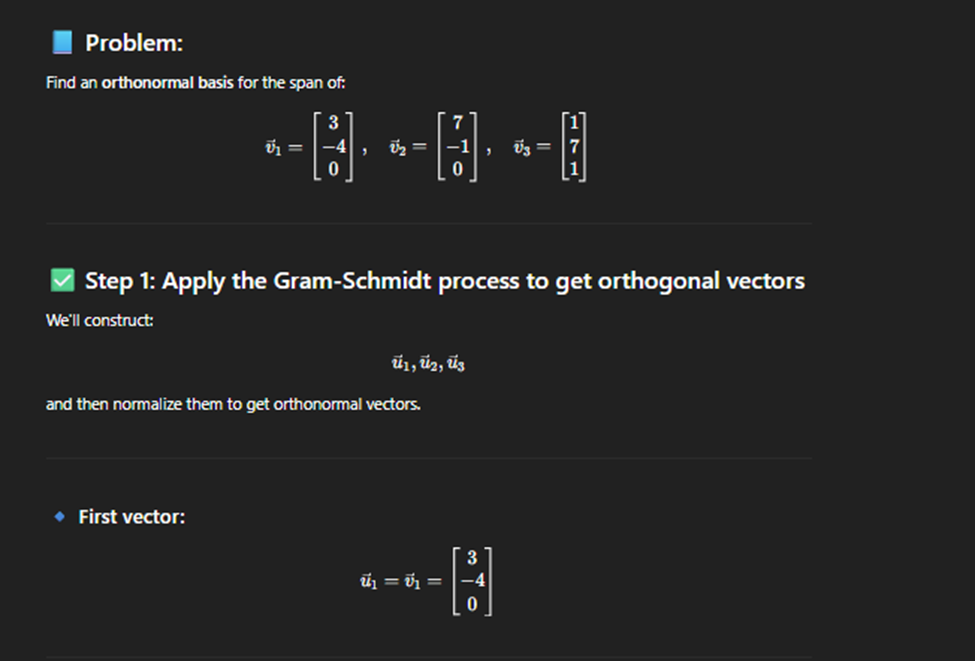
Finding orhtornomal basis

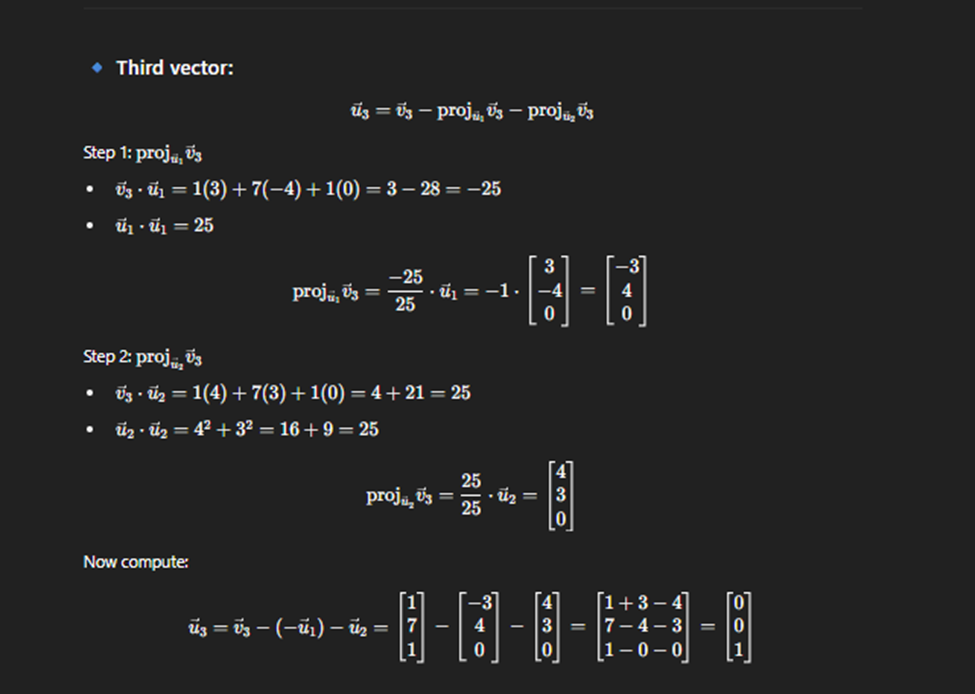
Linear Transformation

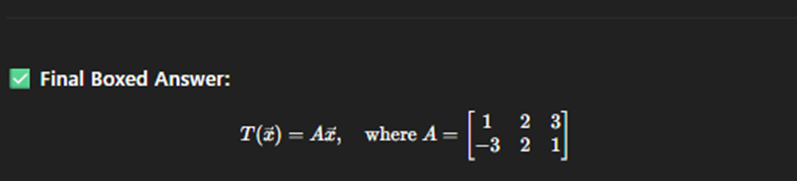
Transformatin not linear

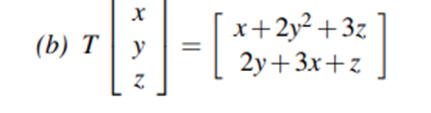
Linear trnasformation and projection

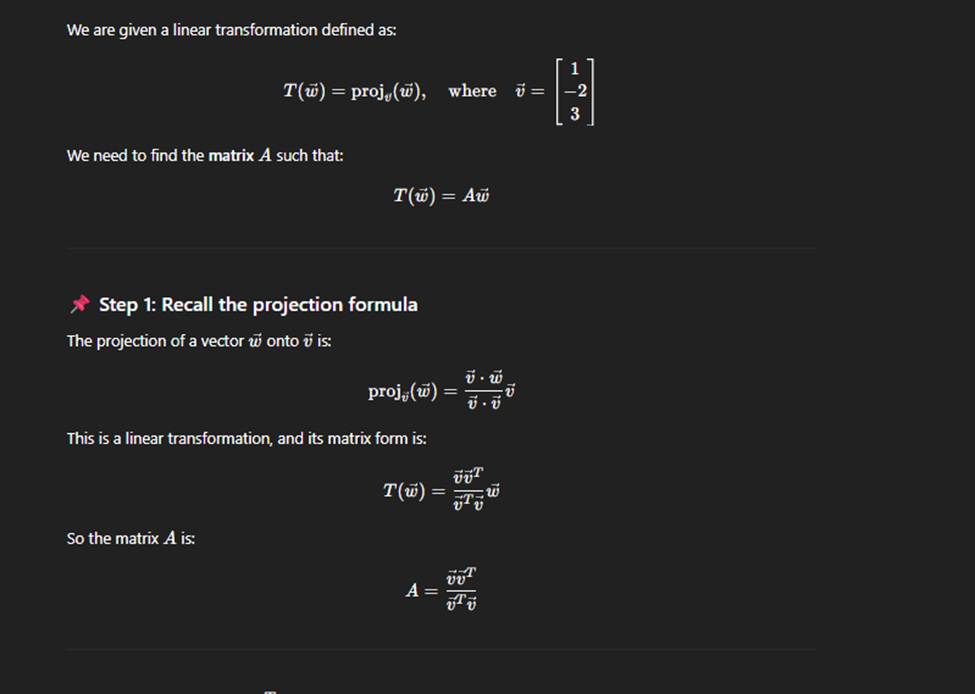
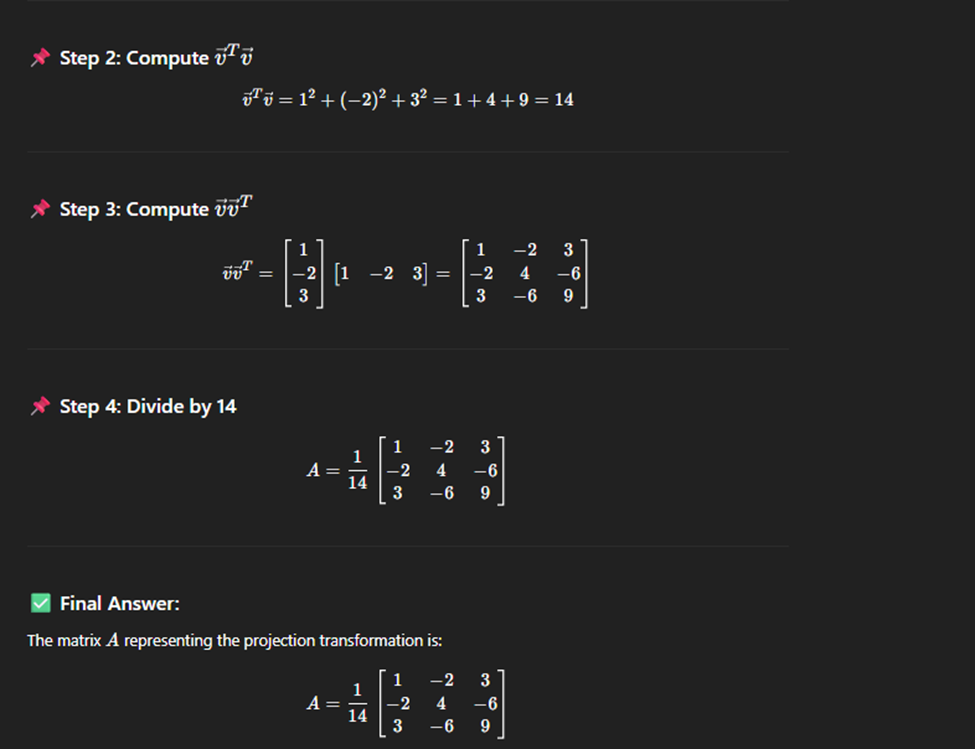
Matrix of linear transformation

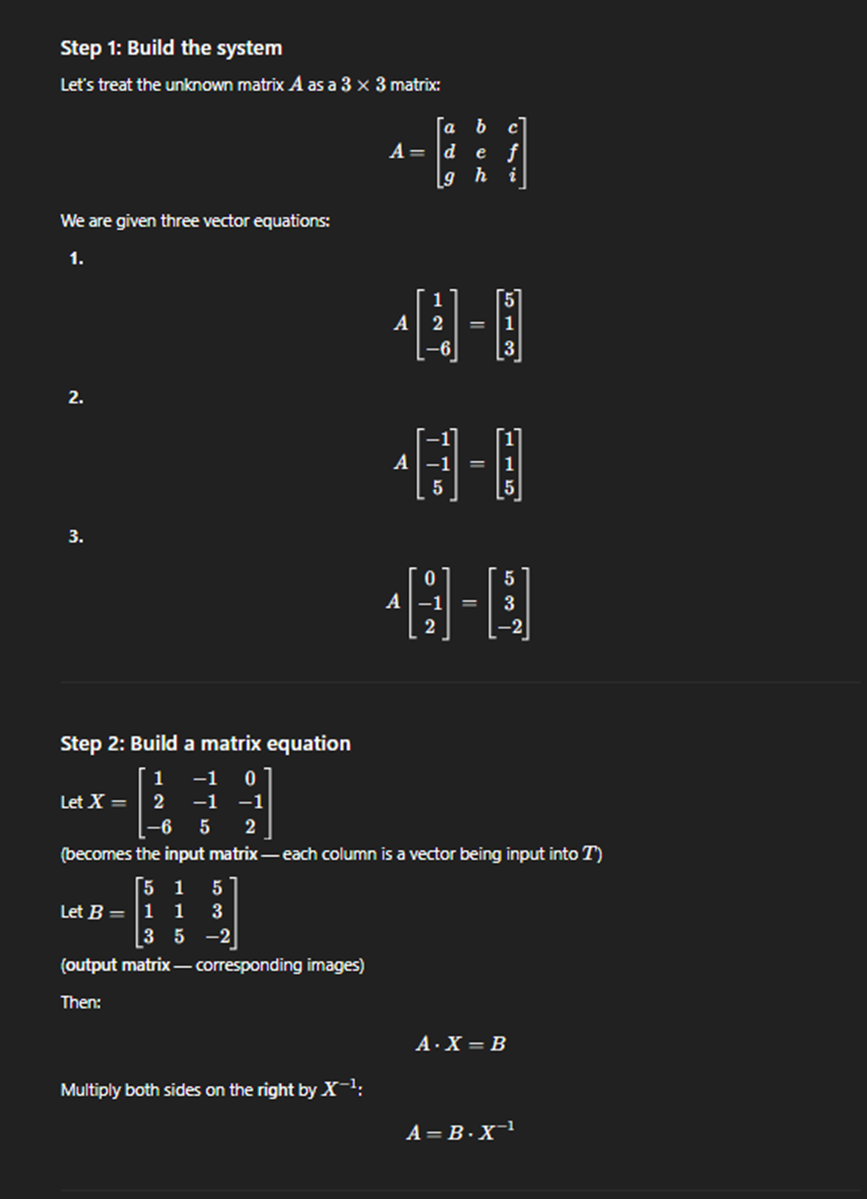
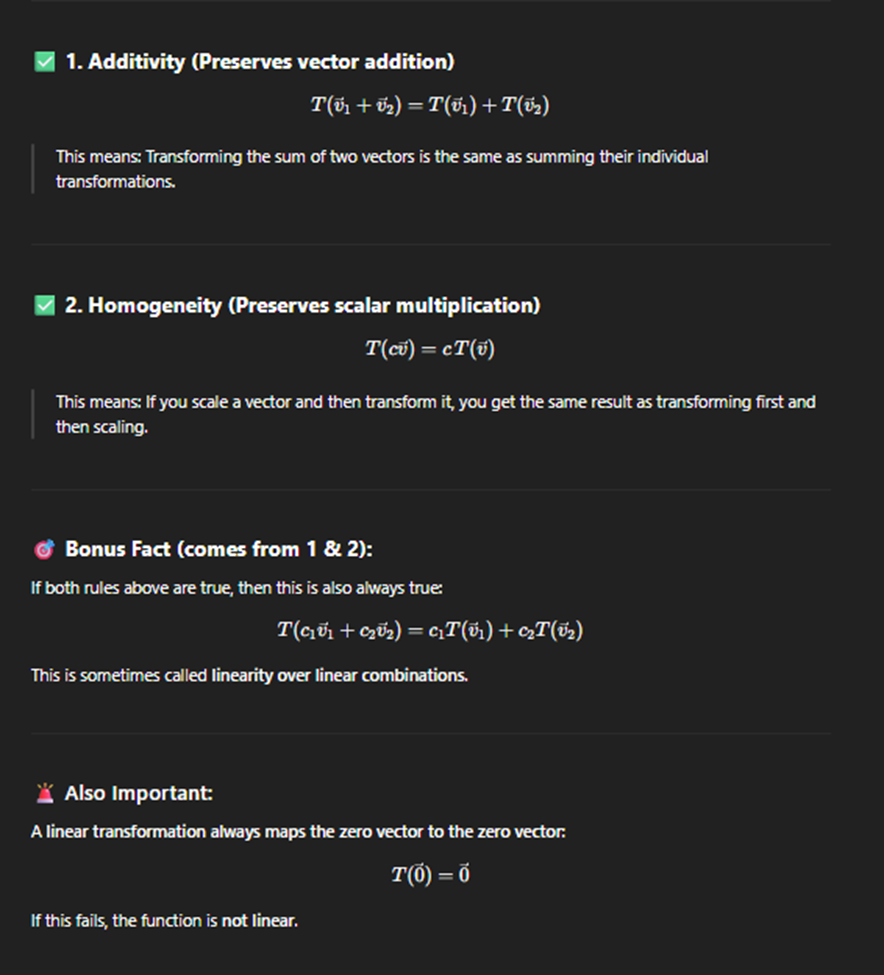
Properteis of Linear Transformation

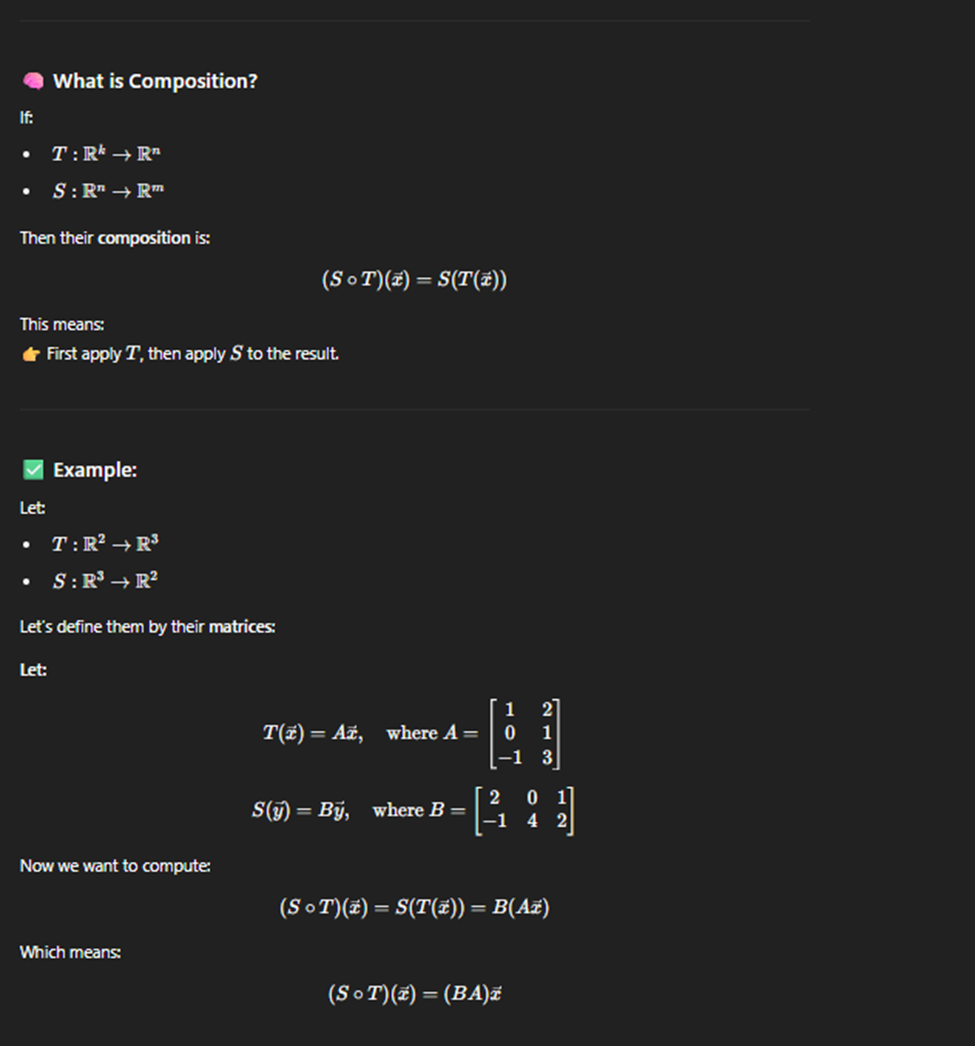
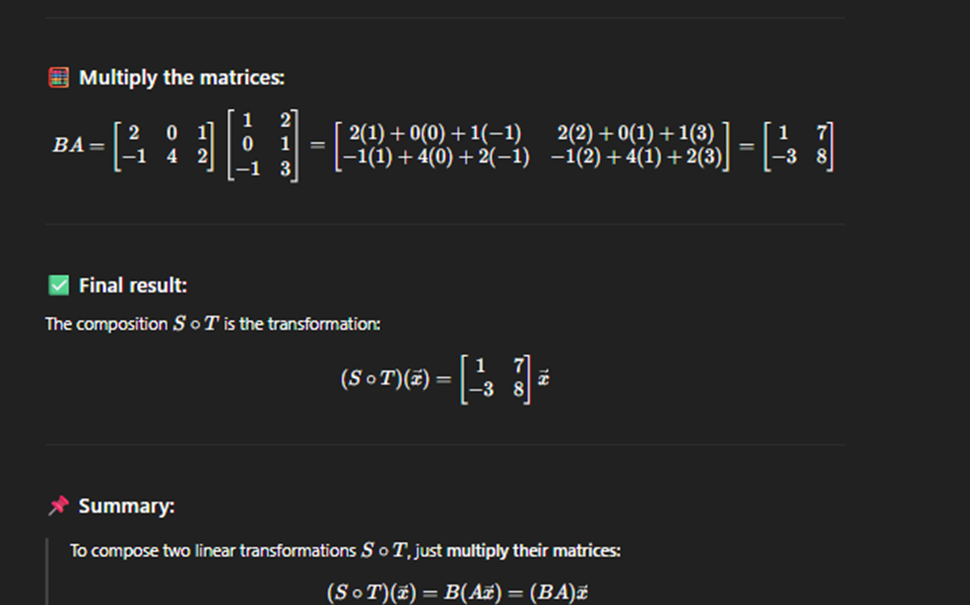
Composite of linear Transformation

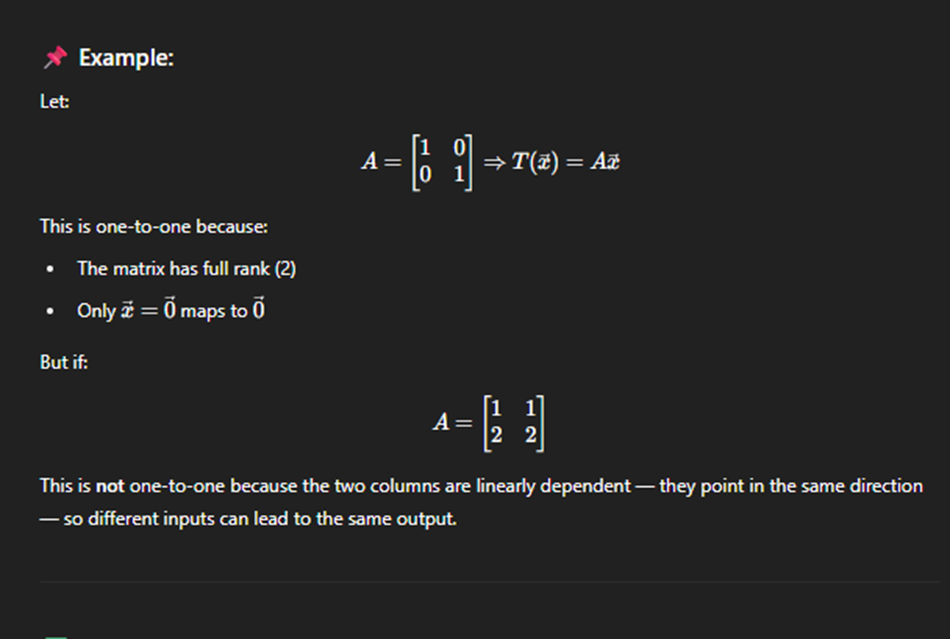
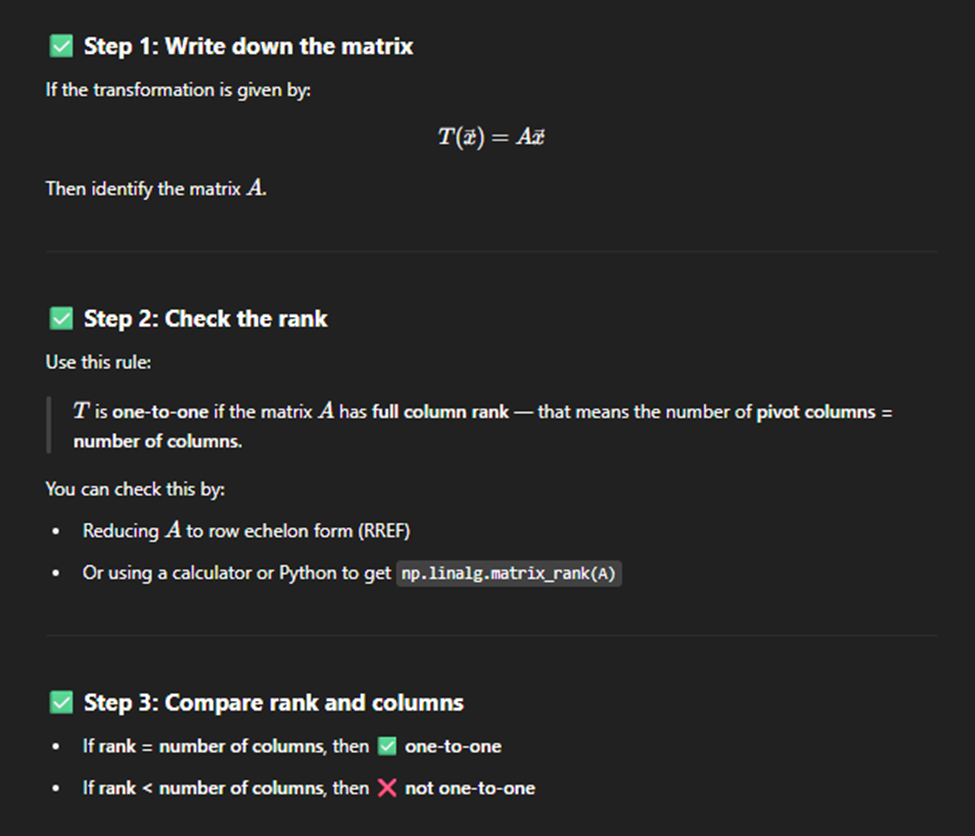
One to one Linear Transform

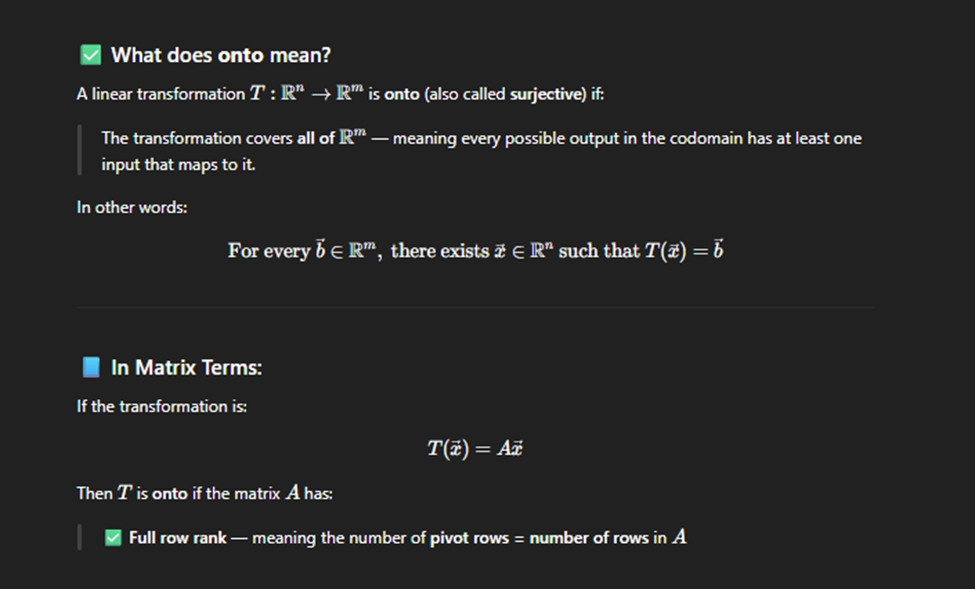
Onto Linear Transform

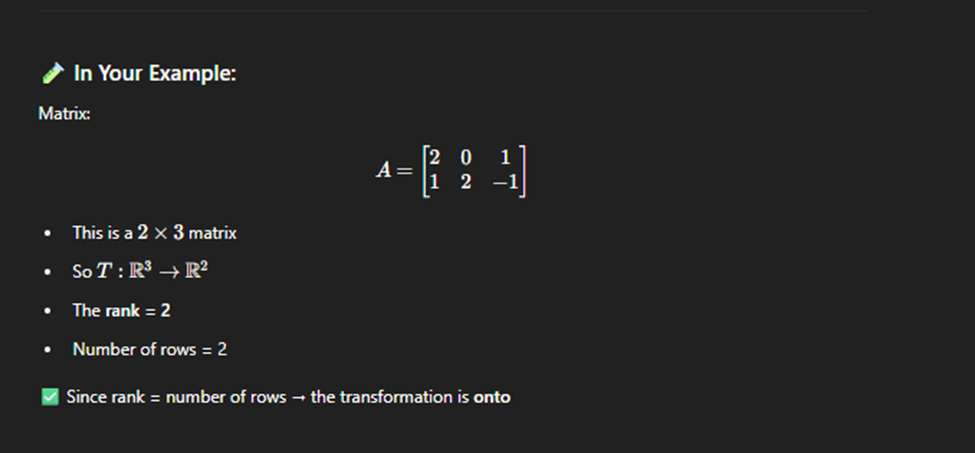
Isophomersim

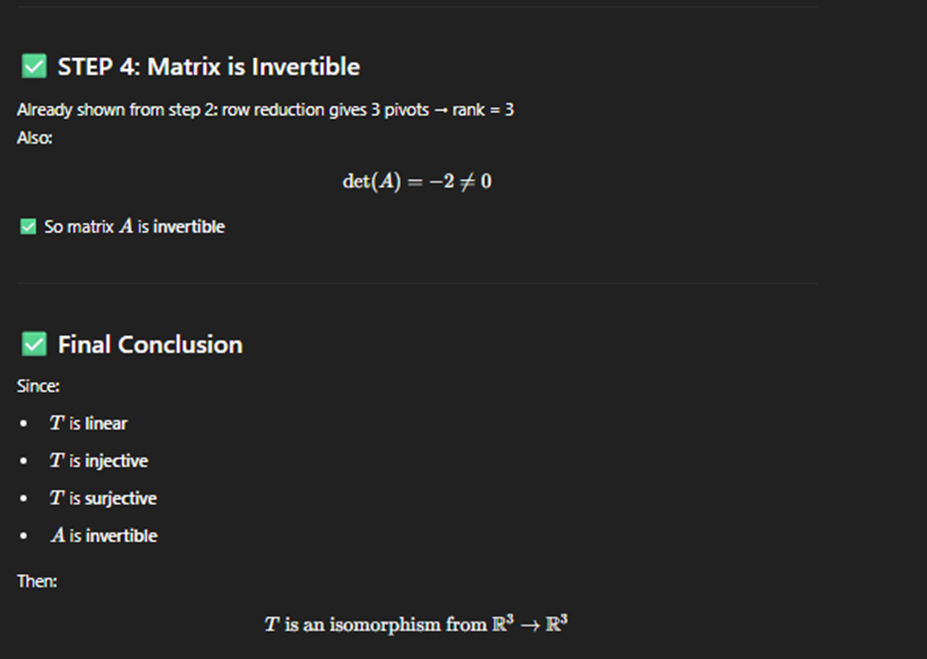
Properties of isophomerism

if det(A) note equal 0 isopherims (probaby dont use this)

Isopomerism subspace

matrix Isophermerism

Isophermism more with images

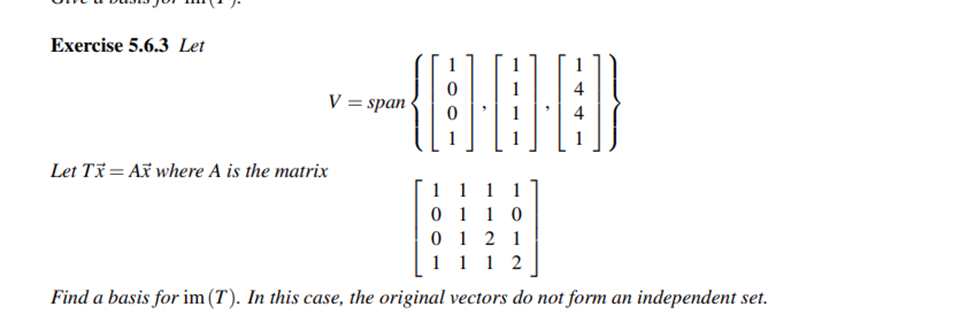
Prove matrix is invetitable

Inverse 2 by 2 matrix

Some more kernal space and others

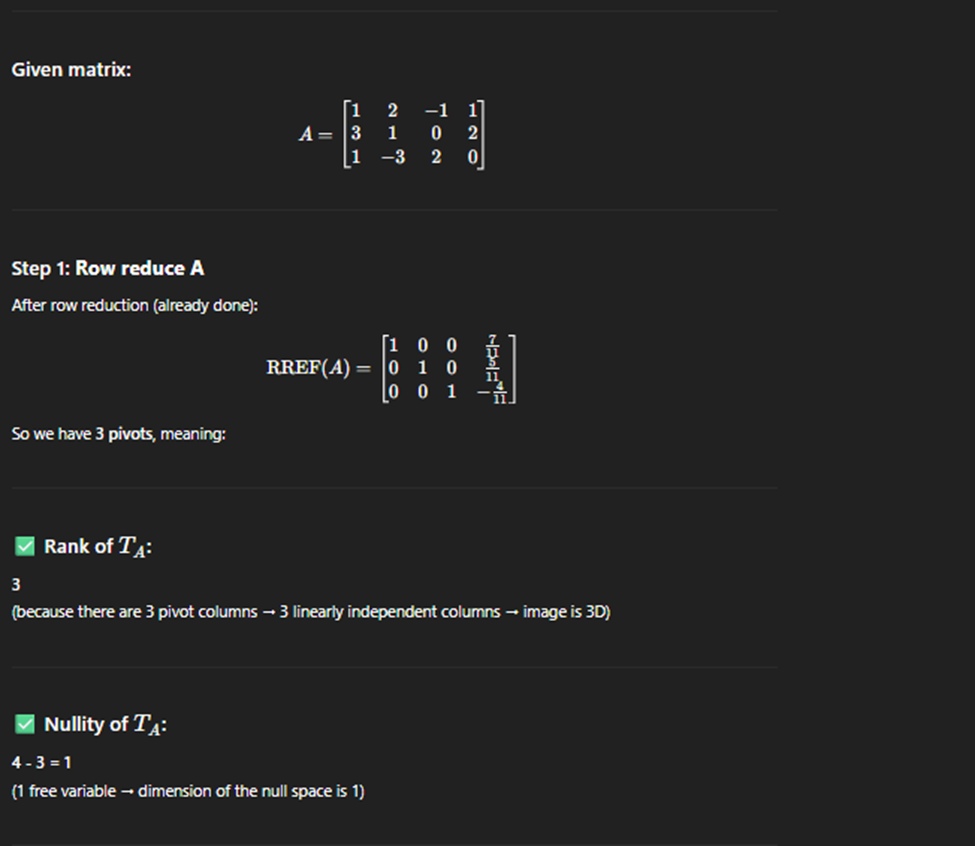
More practice kker basia

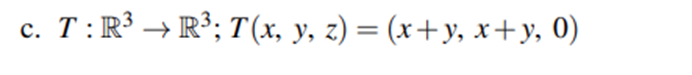
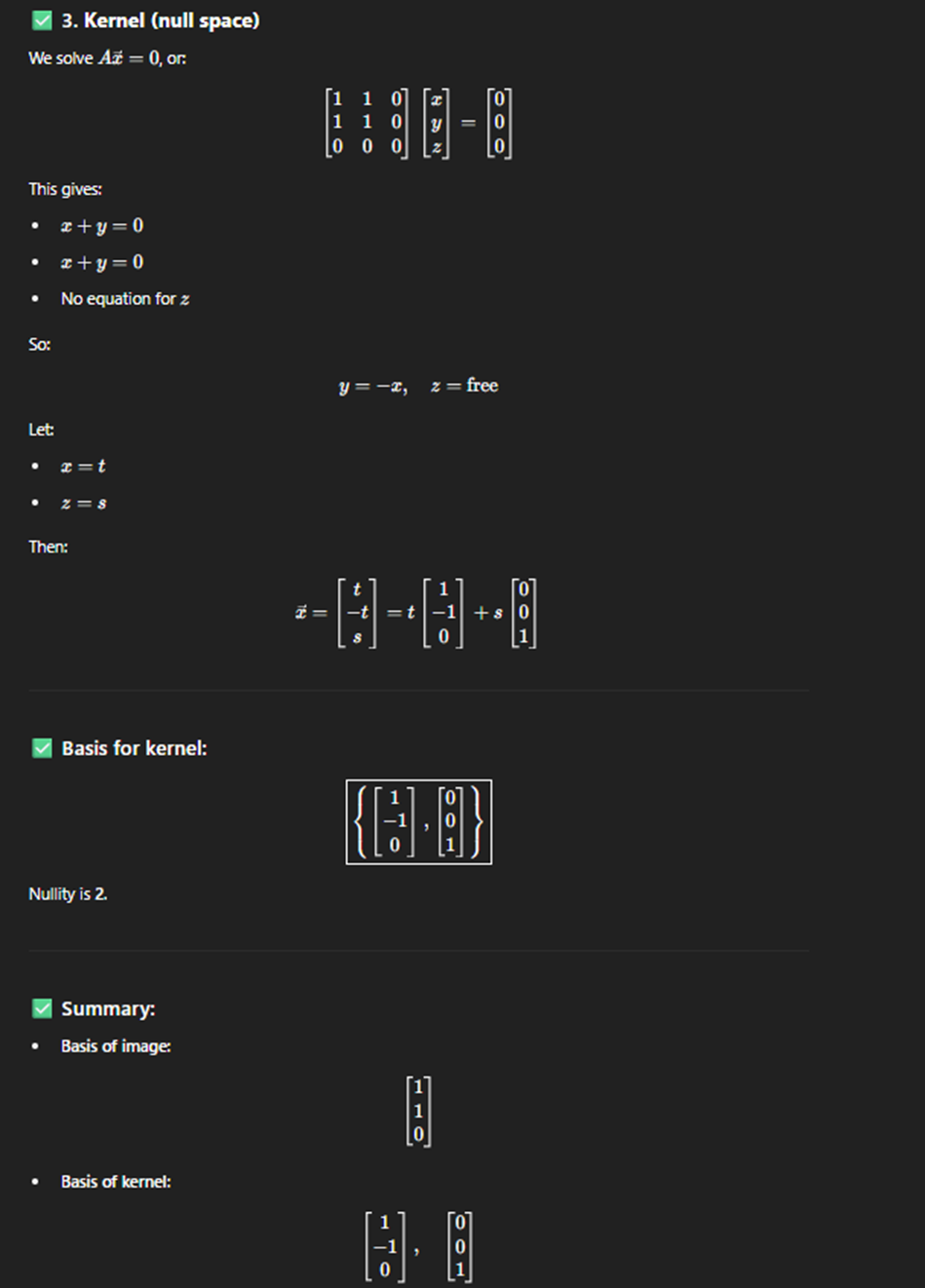
rememeber teh reson its one and all (x+y) is the first rwo and (1 1 0)

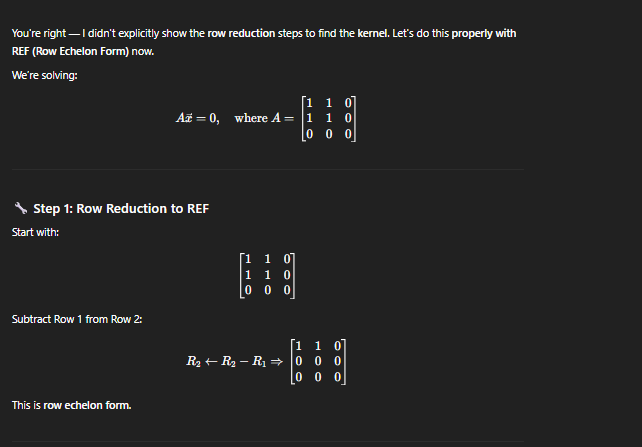
all possible to be orthogonal

Orthogonal projection in liek span

Orthogoanl complement

Poitn in a plane closest to a given point

Least square solution

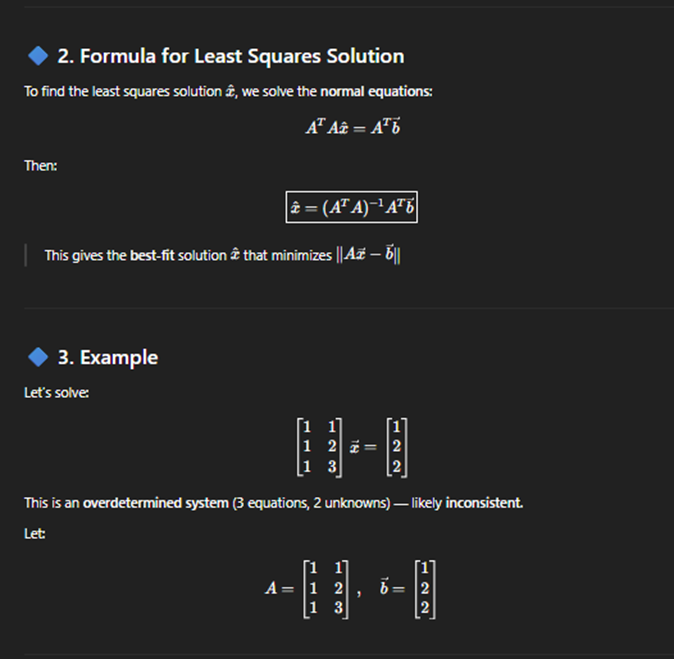
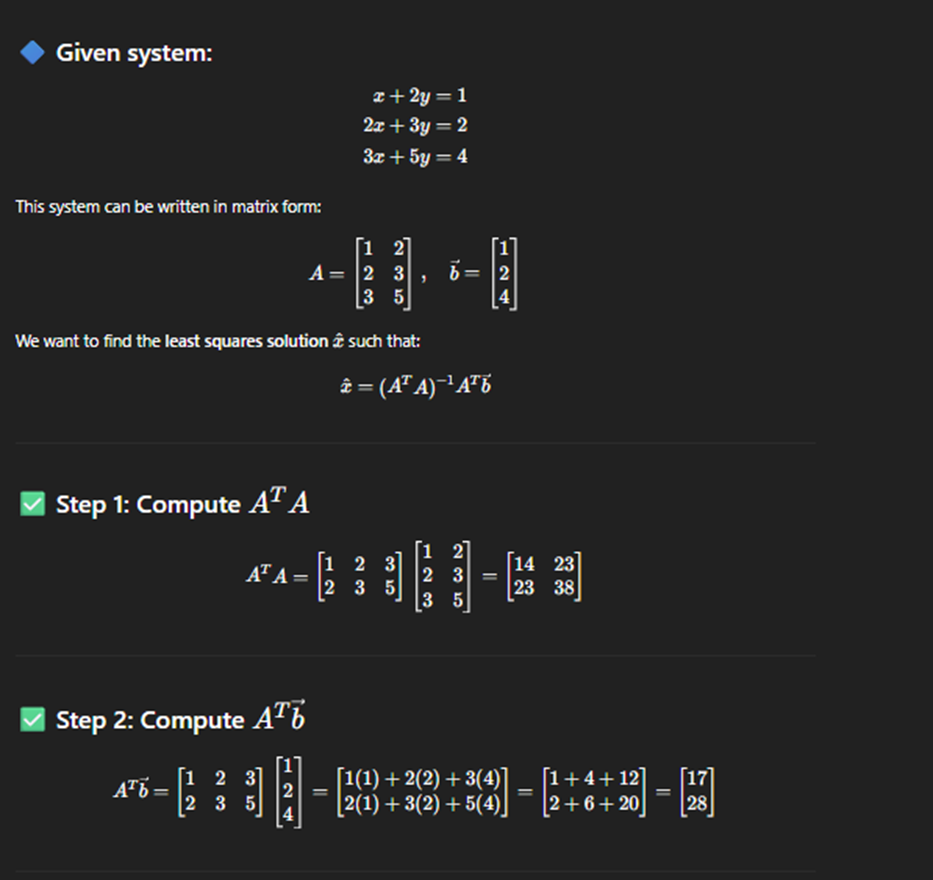
Least square soltuions more

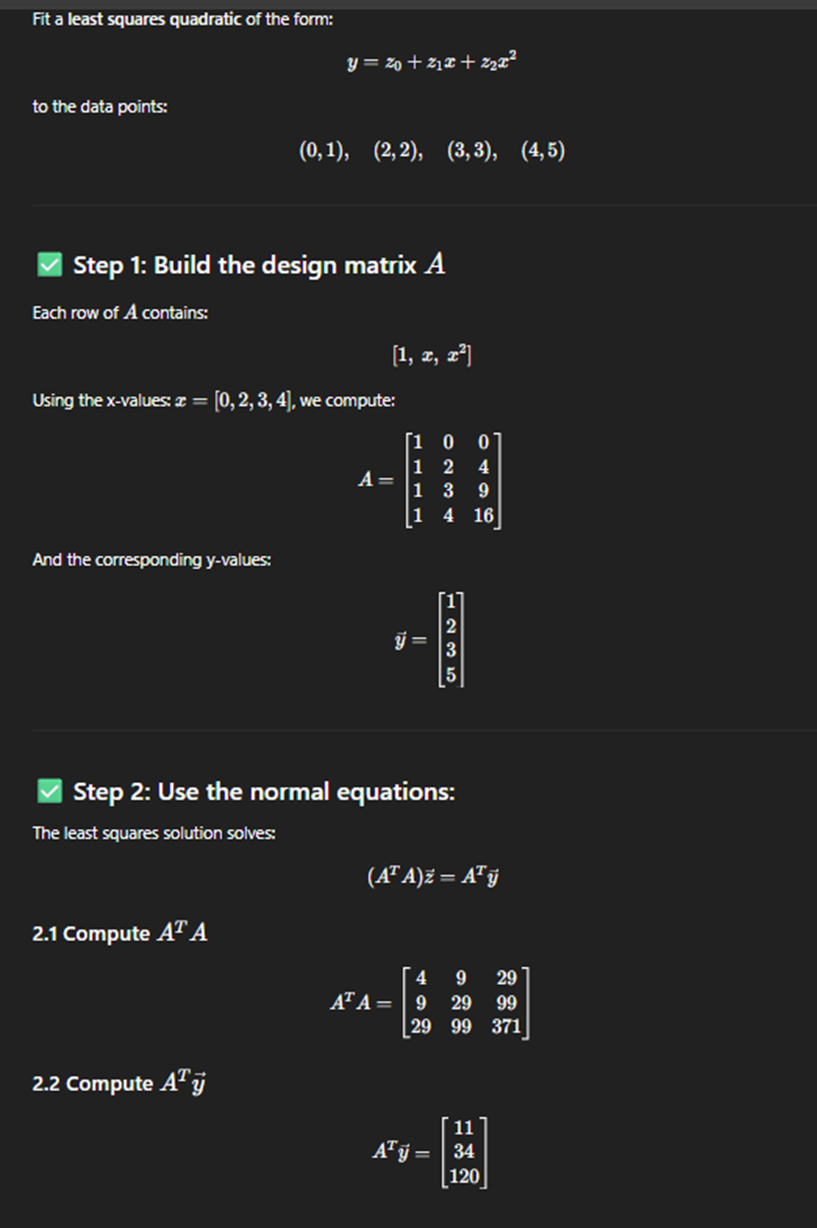
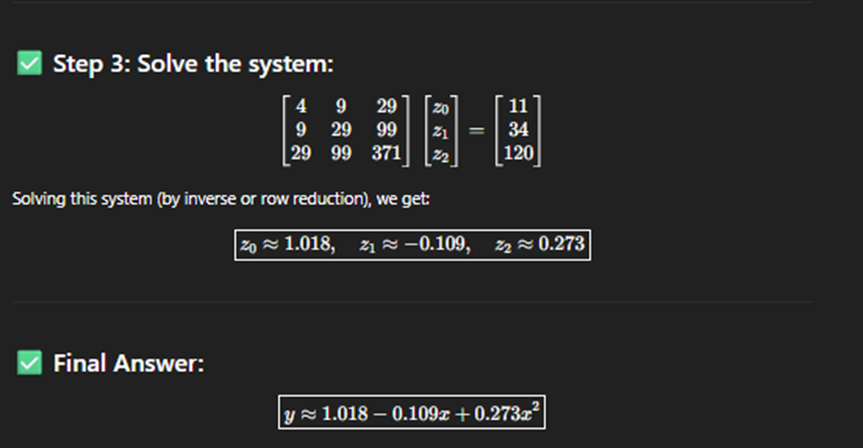
solve some system for fun