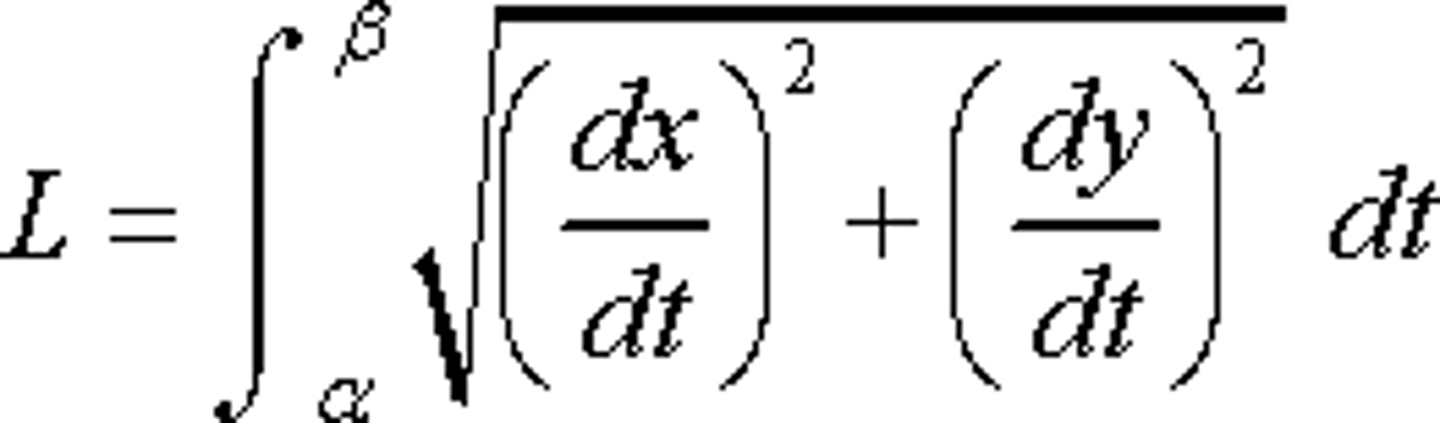Ultimate AP Calculus BC Formulas and Theorems

Sandwich Theorem

a function f that is sandwiched between two other functions, g and h. If g and h have the same limit as x approaches c, then f (the middle function) has that limit too

average rate of change

dividing distance by the time interval.
Slope of secant line between two points, used to estimate instantaneous rate of change at a point.

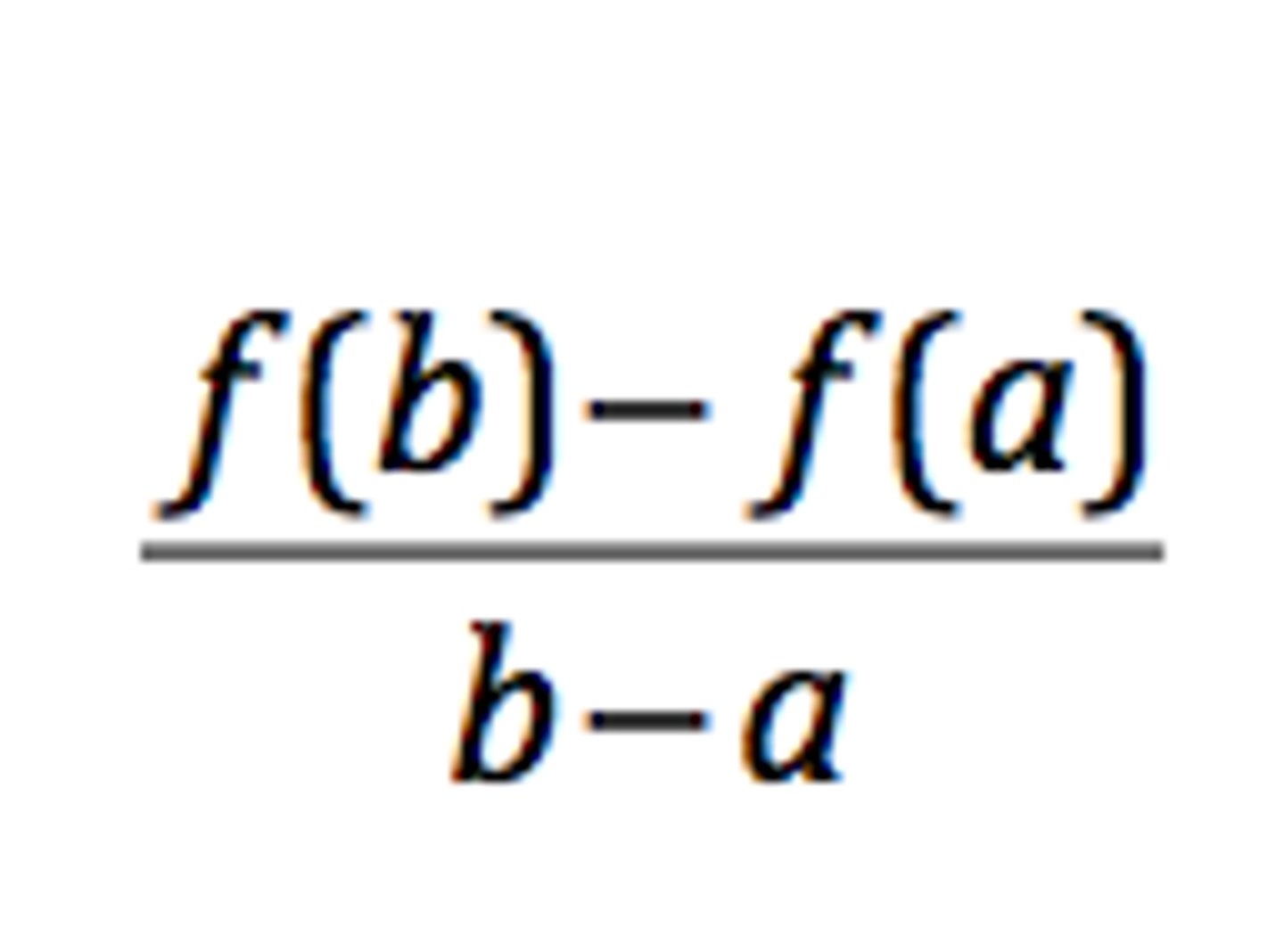
instantaneous rate of change

The rate of change, or slope of a tangent line, or value of the derivative, at a point of a graph.
h= a very small change in time, but it cant be 0 bc itll be undefined.

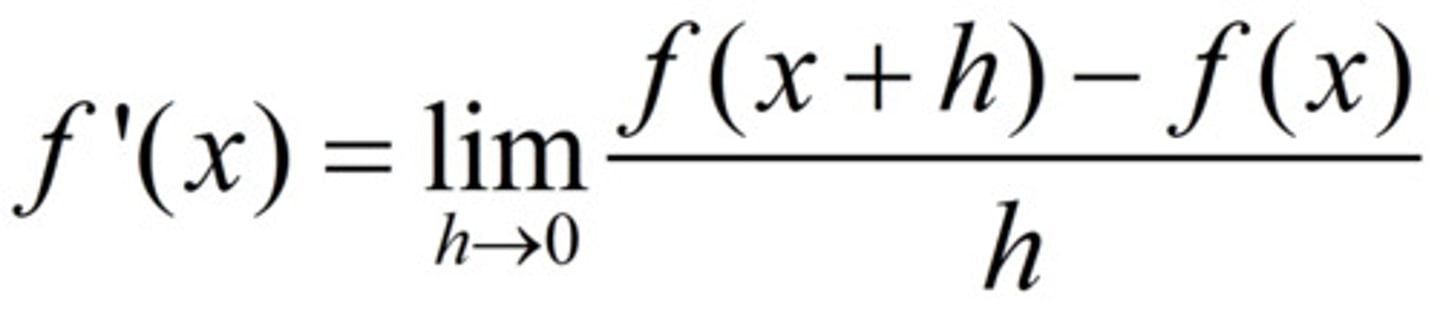
Intermediate Value Theorem

If a function is continuous between a and b, then it takes on every value between f(a) and f(b)

if f is a continuous function on the closed interval [a, b] and d is a number between f (a) and f (b), then the Intermediate Value Theorem guarantees that there is at least one number c between a and b, where f (c) = d.

Derivative at a point

limit as x approaches a of [f(x)-f(a)]/(x-a)

Formal definition of derivative

IRC formula.
limit as h approaches 0 of [f(a+h)-f(a)]/h

Product Rule

u'v + uv'

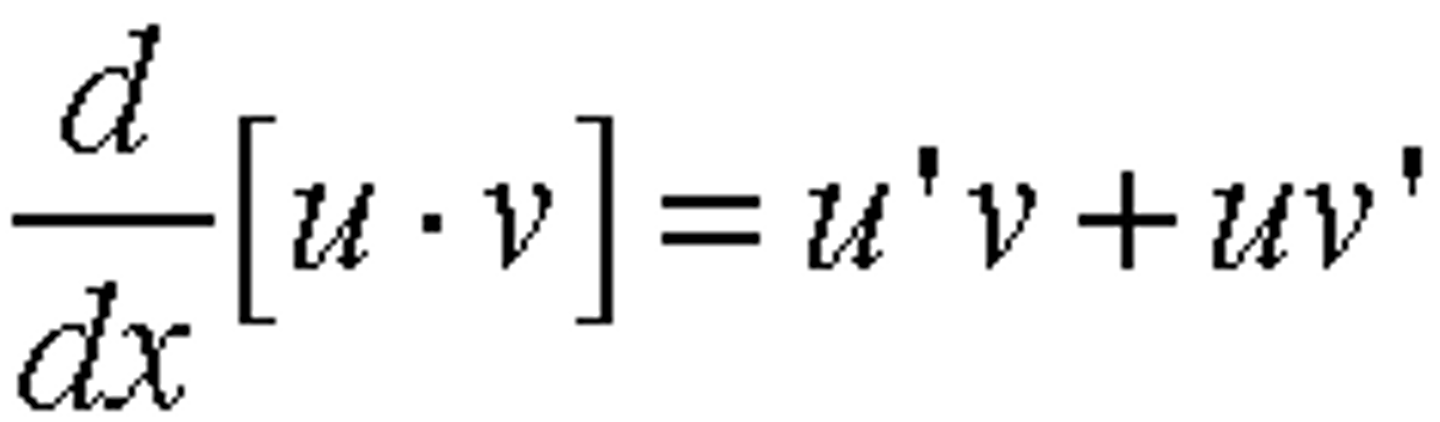
Quotient Rule

(u'v-uv')/v²

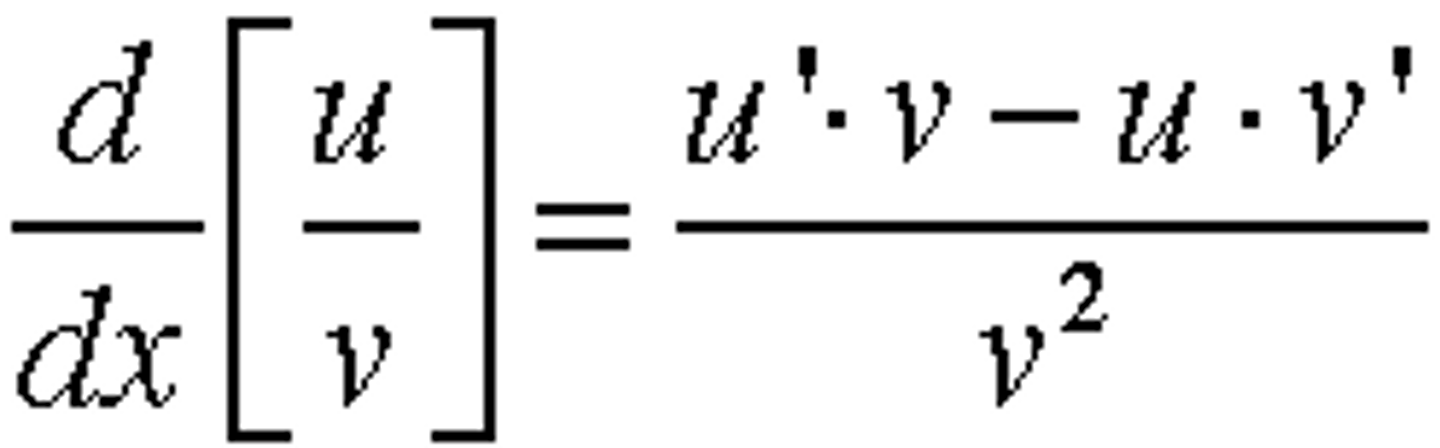
Chain Rule

f '(g(x)) g'(x)
inside function derivative * outside function derivative

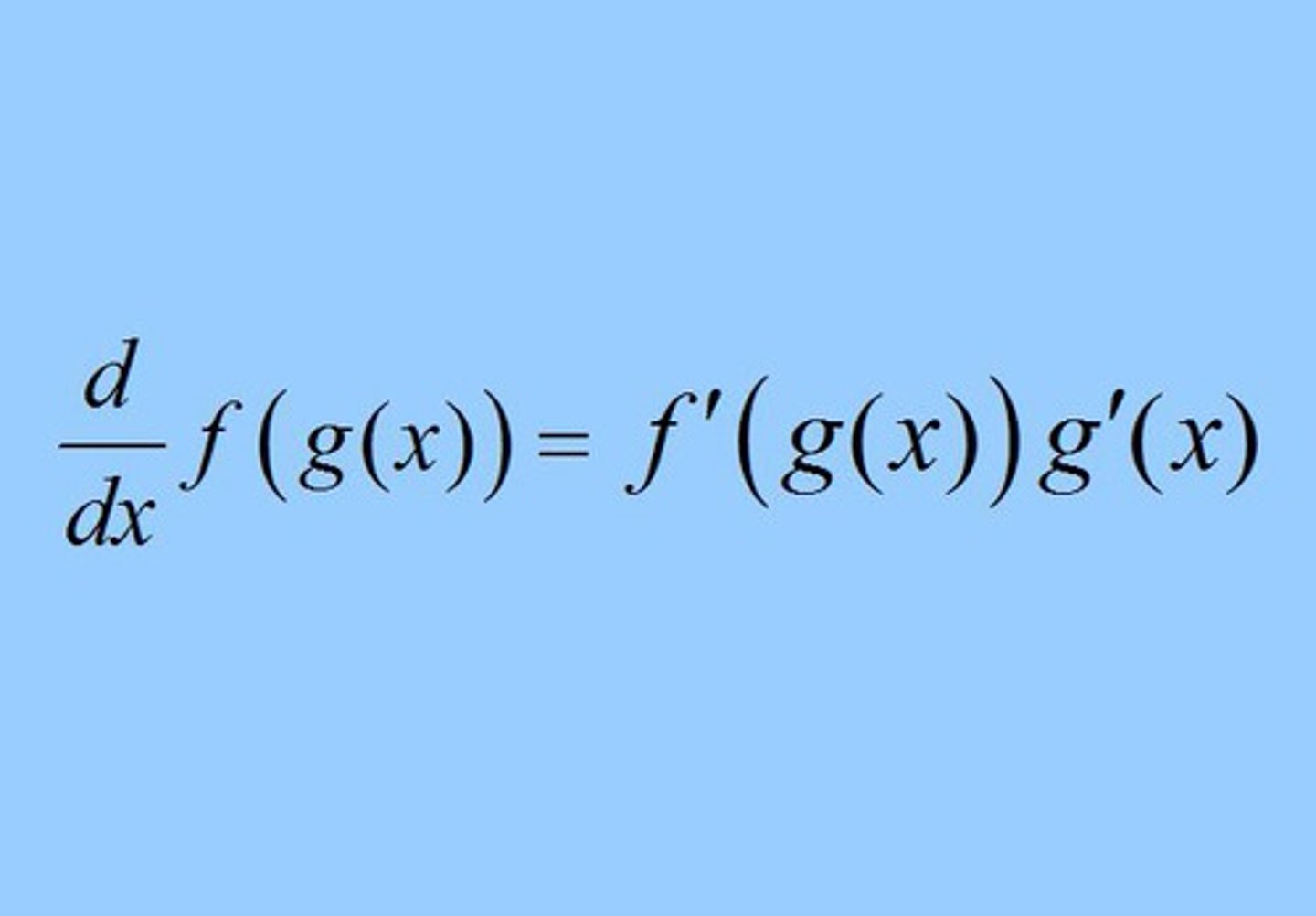
derivative of inverse

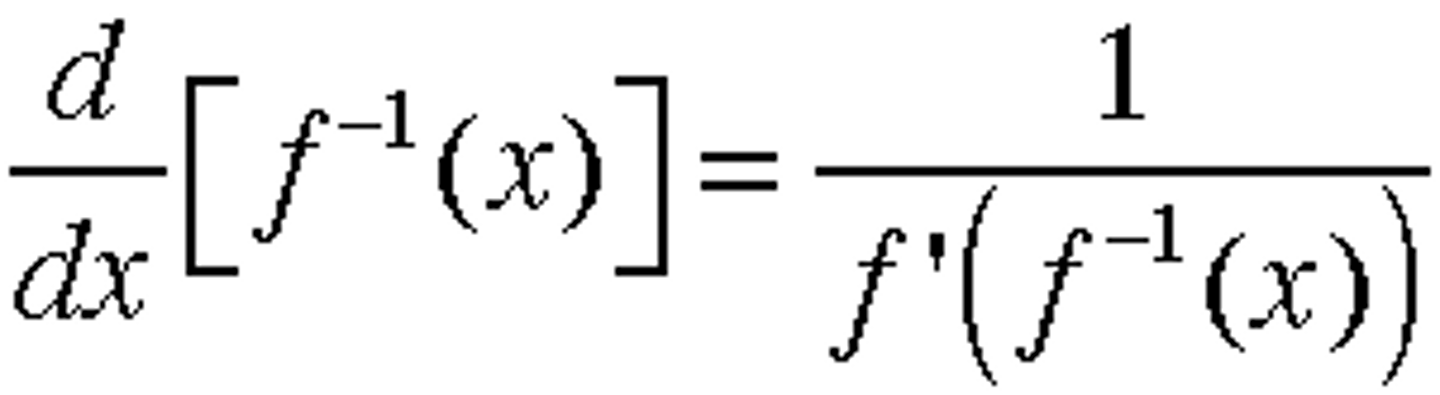
average velocity

∆s/∆t

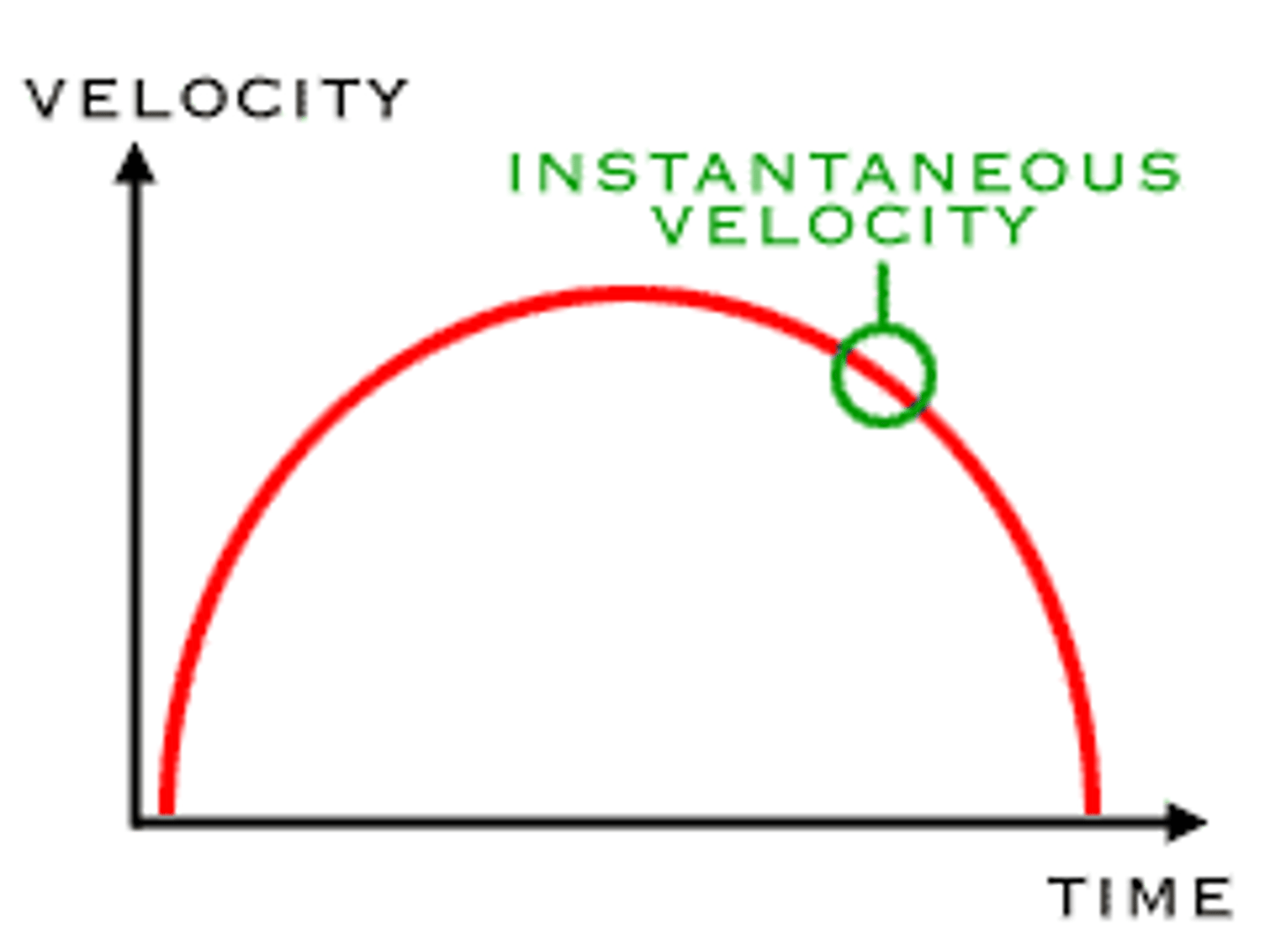
Instantaneous velocity

Derivative of position s(t) at a point.
ds/dt

speed

Absolute value of velocity.
|v(t)|

Acceleration

derivative of velocity. (units= m/s²)

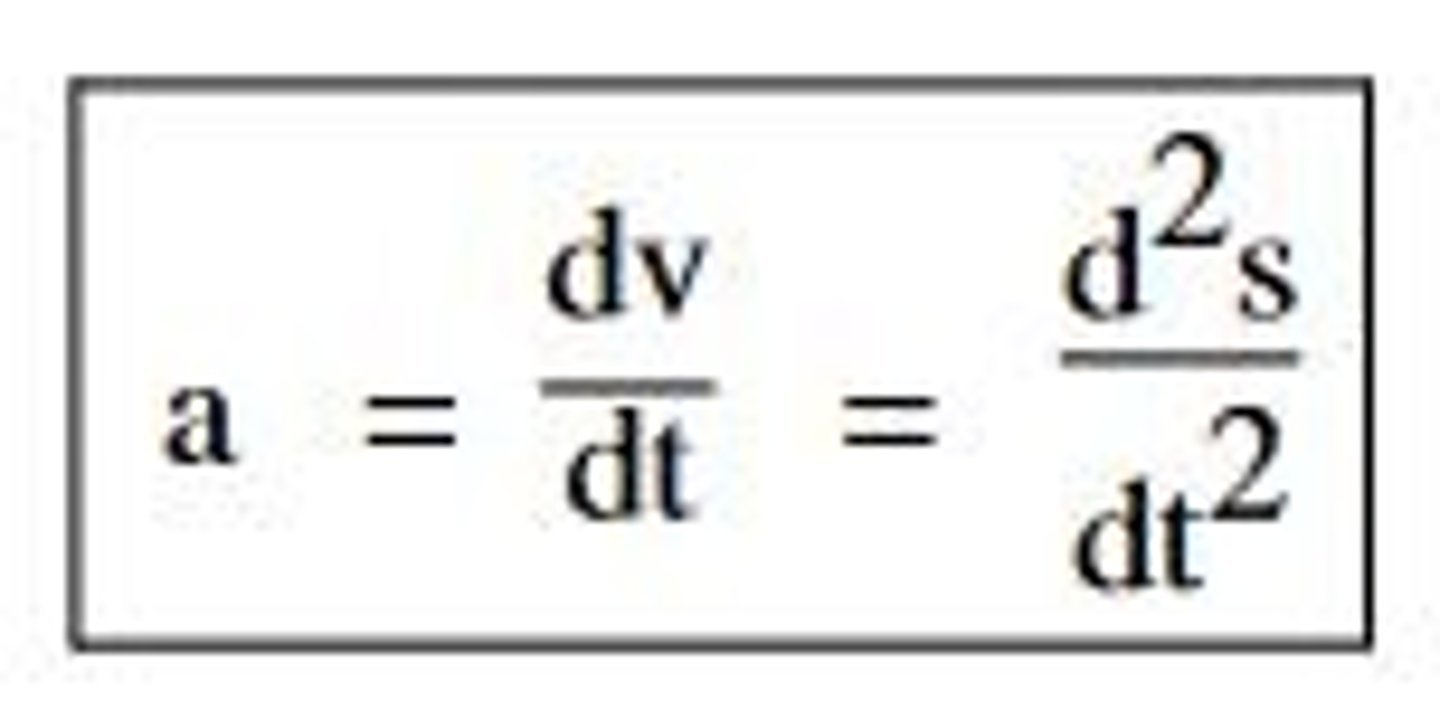
first derivative test for local extrema

For a continuous function f:
1) If f' changes sign, f has a local maximum or minimum value at c
2) If f' does not change sign at a critical point c, then f has no local extreme values at c

Second Derivative Test for local extrema

1. if f'(c)=0 and f''(c)>0, then f has local minimum at c. Concave up.
2. if f'(c)=0 and f''(c)<0, then f has a local maximum at c. Concave down.
3. FAILS if f''(c) = 0 or if f''(c) DNE

HOW TO USE SECOND DERIVATIVE TEST
1. use first derivative to find critical points
2. sub critical points into second derivative. if f''(x)<0, it is concave down, and a MAX.

Intermediate Value Theorem for Derivatives

If f is differentiable on [a,b], then f'(x) takes on all values between f'(a) and f'(b).

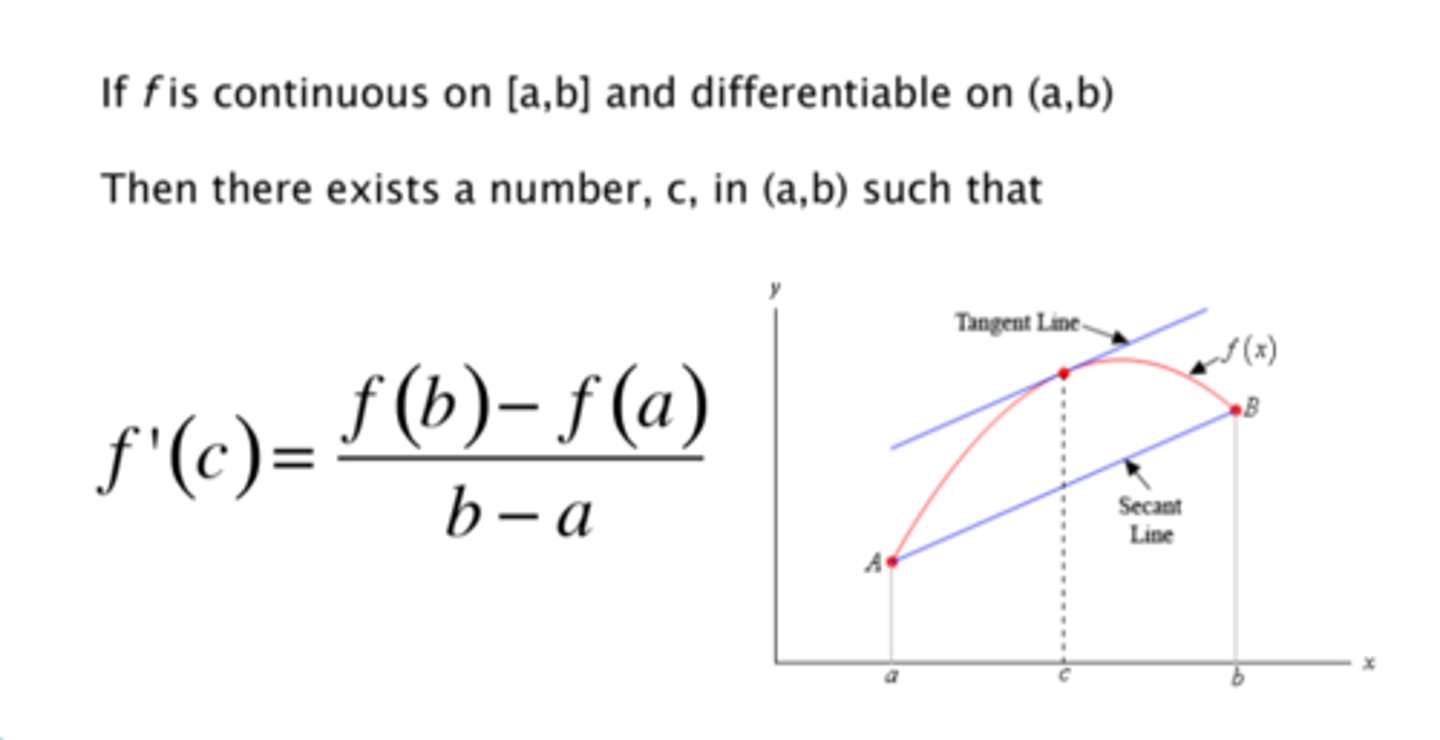
mean value theorem

CHECK CONDITIONS FIRST
if f(x) is continuous on the closed interval and differentiable on the open interval,,,,,, the slope of tangent line equals the slope of the secant line (secant line goes through 2 points), at least once in the interval (a, b)

f '(c) = [f(b) - f(a)]/(b - a)

IRC=ARC

mean value theorem for derivatives

IRC = ARC
continuous on closed, differentiable on the open. ALWAYS CHECK CONDITIONS. ONLY WORKS ON CLOSED INTERVALS

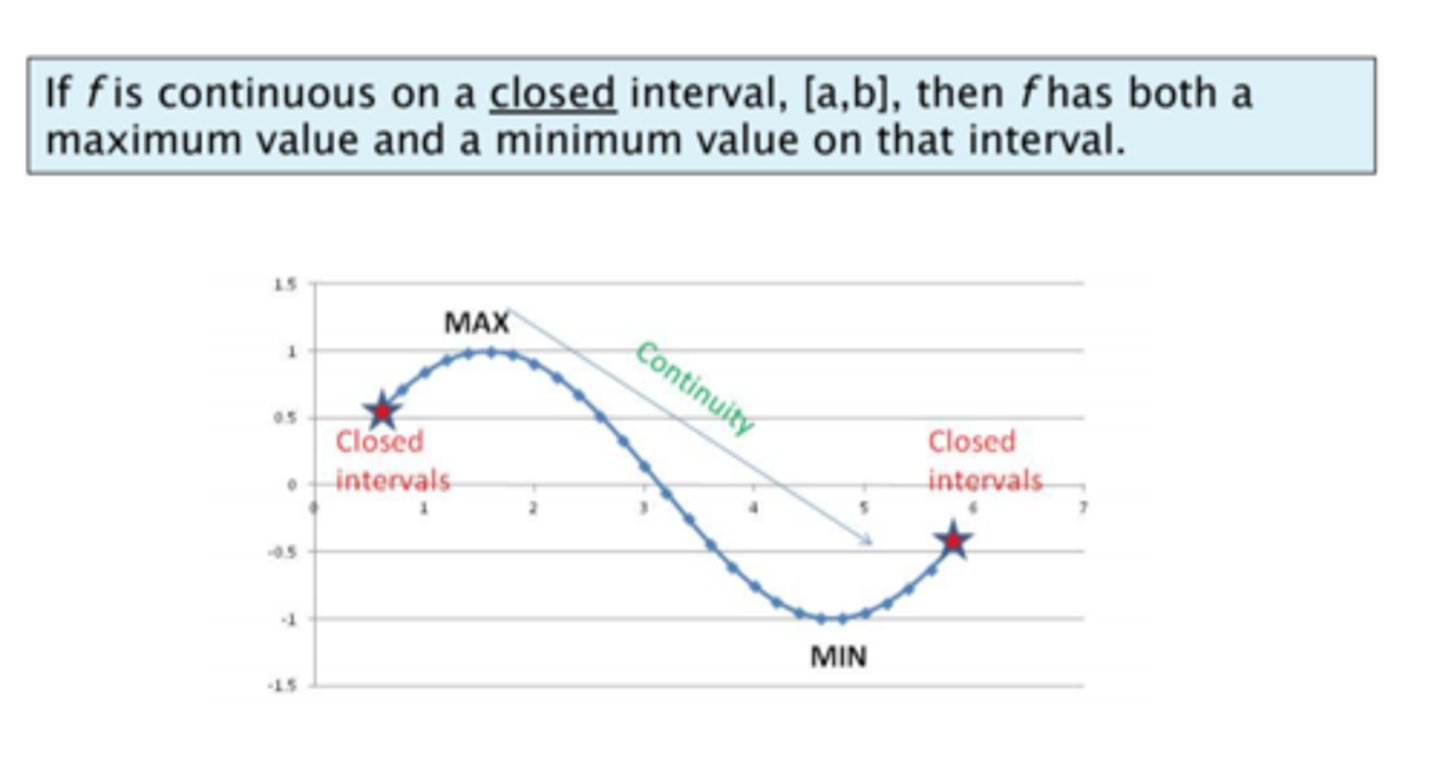
Extreme Value Theorem

If f is continuous over a CLOSED interval, then f has at LEAST one maximum and minimum value over that interval

Rolle's Theorem

If f(x) is continuous on the closed interval [a,b], AND differentiable on the open (a,b), AND f(a)=f(b), then there is at least one number x=c in (a,b) where f'(c)=0

rectangle surface area formula

SA = 2lw + 2wh + 2lh

right cylinder surface area formula

SA= 2πrh + 2πr²

right cylinder with no top surface area formula

SA= 2πrh + πr²

open top and square base surface area formula

SA= x² +4xh

sphere surface area formula

SA= 4πr²

right cylinder volume formula

V= πr²h

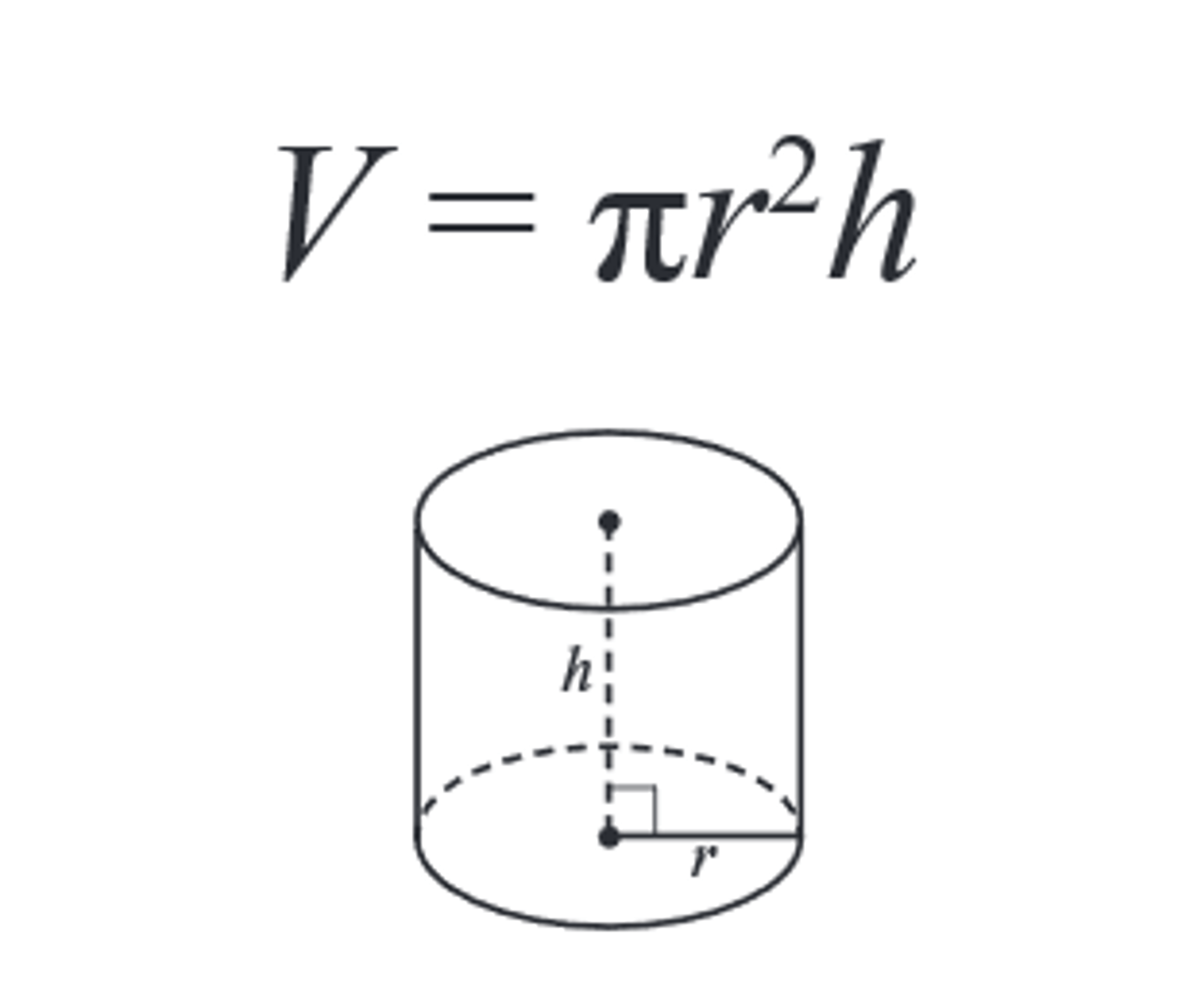
right cylinder with no top volume formula

V= πr²h (the same)

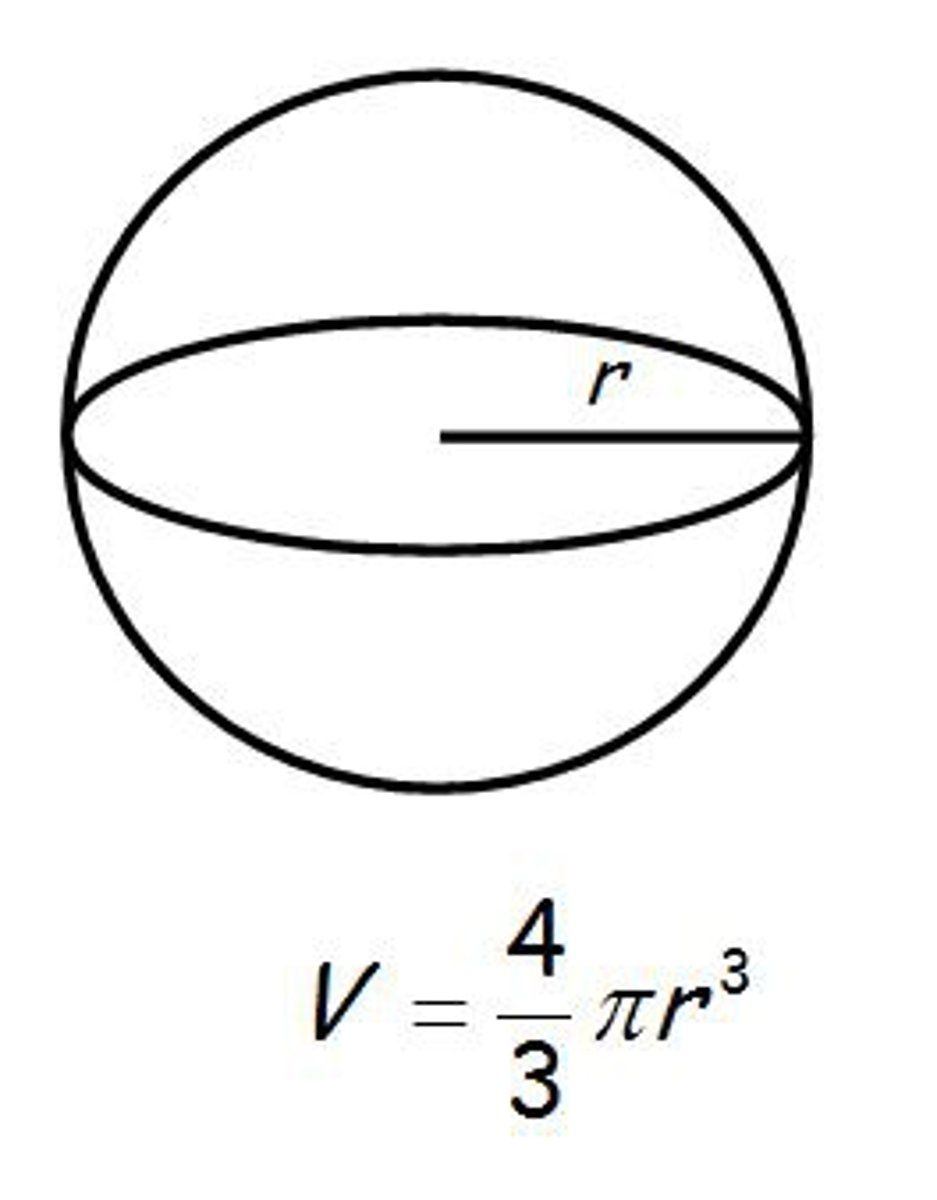
sphere volume formula

V = 4/3πr³

cone volume formula

V = 1/3πr²h

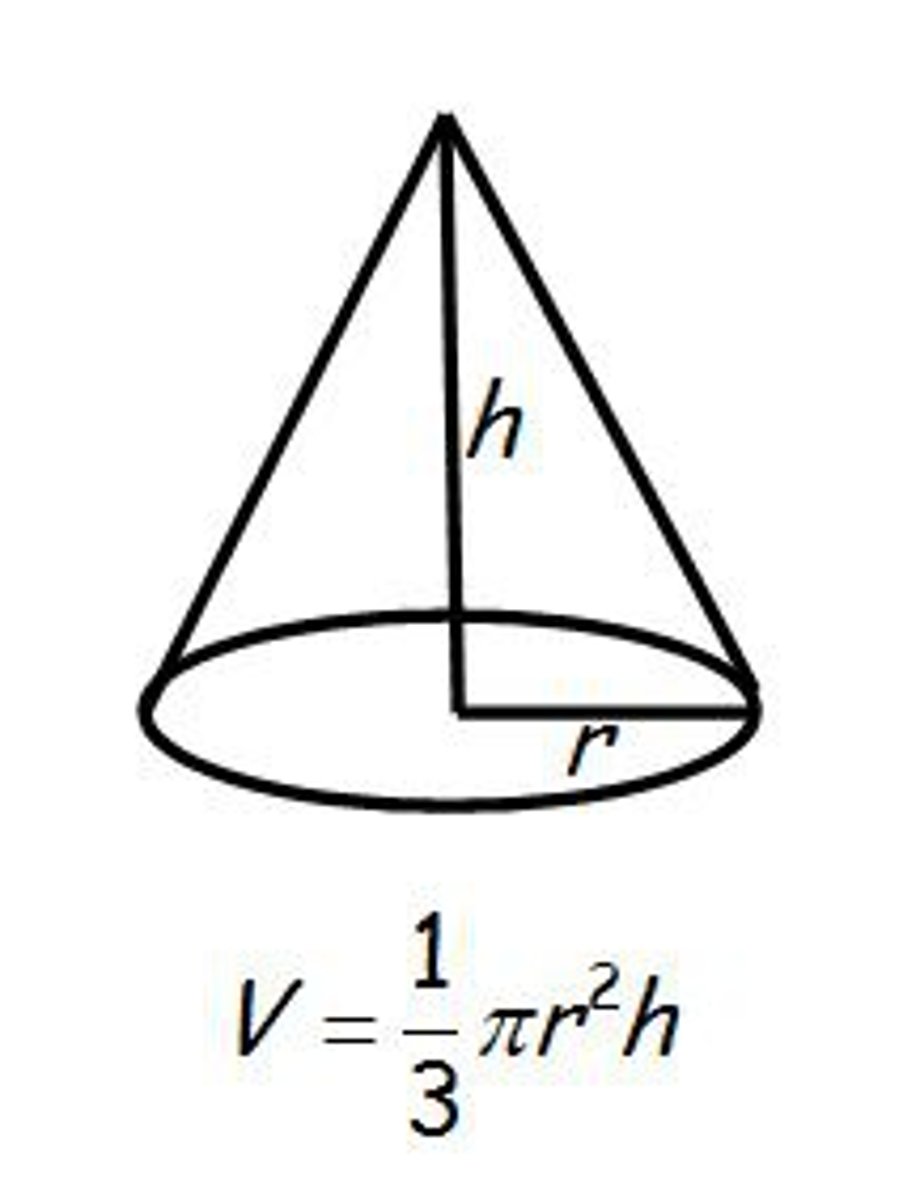
distance formula

√(x₂-x₁)²+(y₂-y₁)²

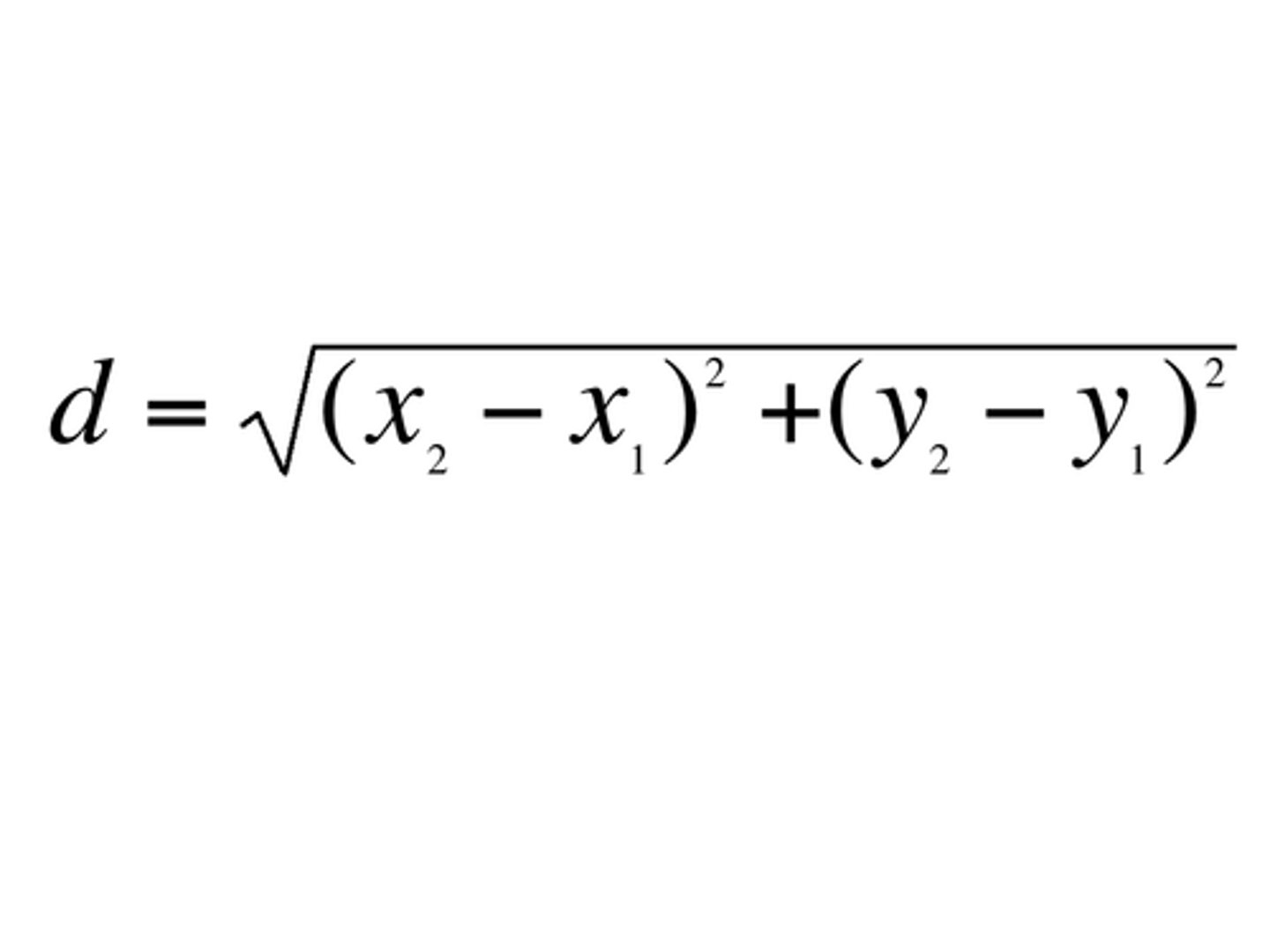
Newton's Method

x₁= x₀- f(x)/f'(x)
1. guess a root
2. find a y value for your guess
3. find the derivative for f'(c)
4. divide y value by derivative
5. subtract guess by y value divided by derivative
6. repeat until you get close to the actual root

GUESS - Y VALUE/DERIVATIVE

euler's method

A method for solving differential equations dy/dx by starting at initial conditions and iterating y_(n+1) = y_n + f(x_n,y_n)*h and x_(n+1) = x_n + h, where h is the step size of the independent variable

1. start with given point
2. sub point into dy/dx
3. find dx by dividing length of interval by the number of steps
4. multiply the dy/dx value by dx to get dy
5. add dy to the original y value, and add dx to the x value
6. repeat for the number of iterations

underestimate when the curve is concave up, and an overestimate when the curve is concave down.

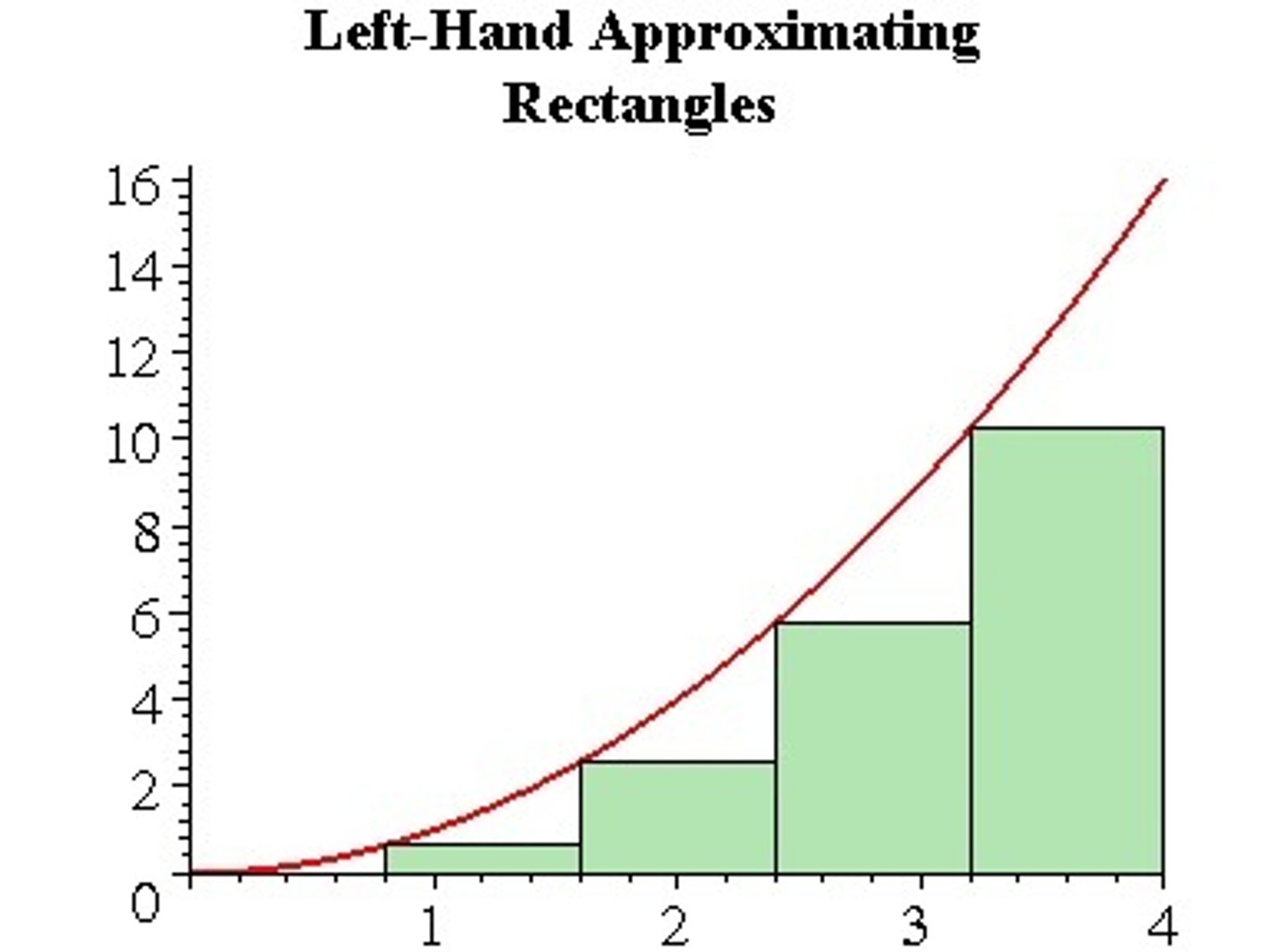
left riemann sum

use rectangles with left-endpoints to evaluate an integral (estimate area)
◦ UNDERESTIMATE OF AREA UNDER CURVE IF CURVE IS INCREASING
◦ OVERESTIMATE OF AREA UNDER CURVE IF CURVE IS DECREASING
◦ Interval *(adding up all y values on curve that the left side of rectangle touches. add all y values except last one)

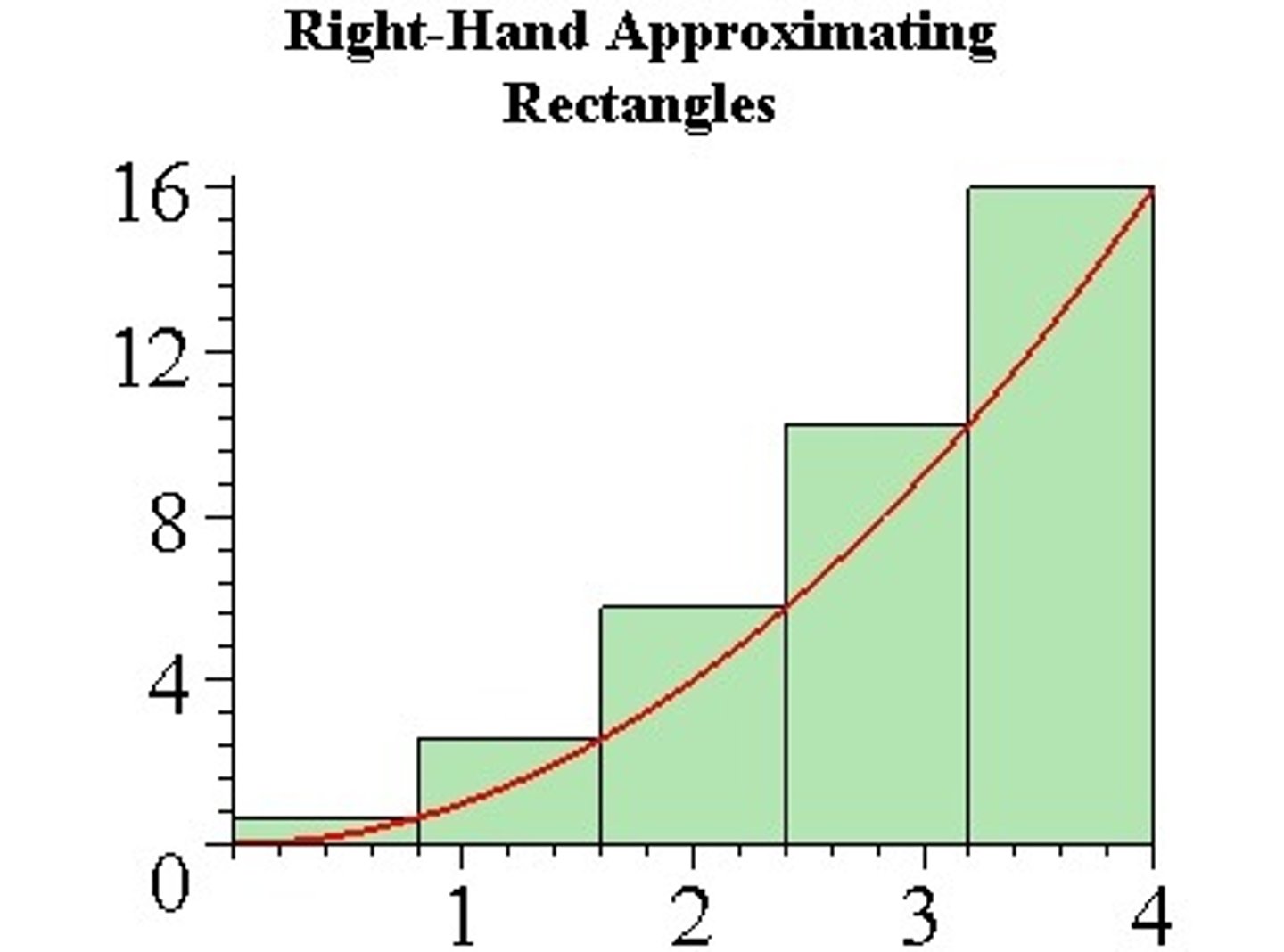
right riemann sum

use rectangles with right-endpoints to evaluate an integral (estimate area)
◦ UNDERESTIMATE OF AREA UNDER CURVE IF CURVE IS DECREASING
◦ OVERESTIMATE OF AREA UNDER CURVE IF CURVE IS INCREASING
◦ Interval *(adding up all y values on curve that the right side of rectangle touches. add all y values except the first)

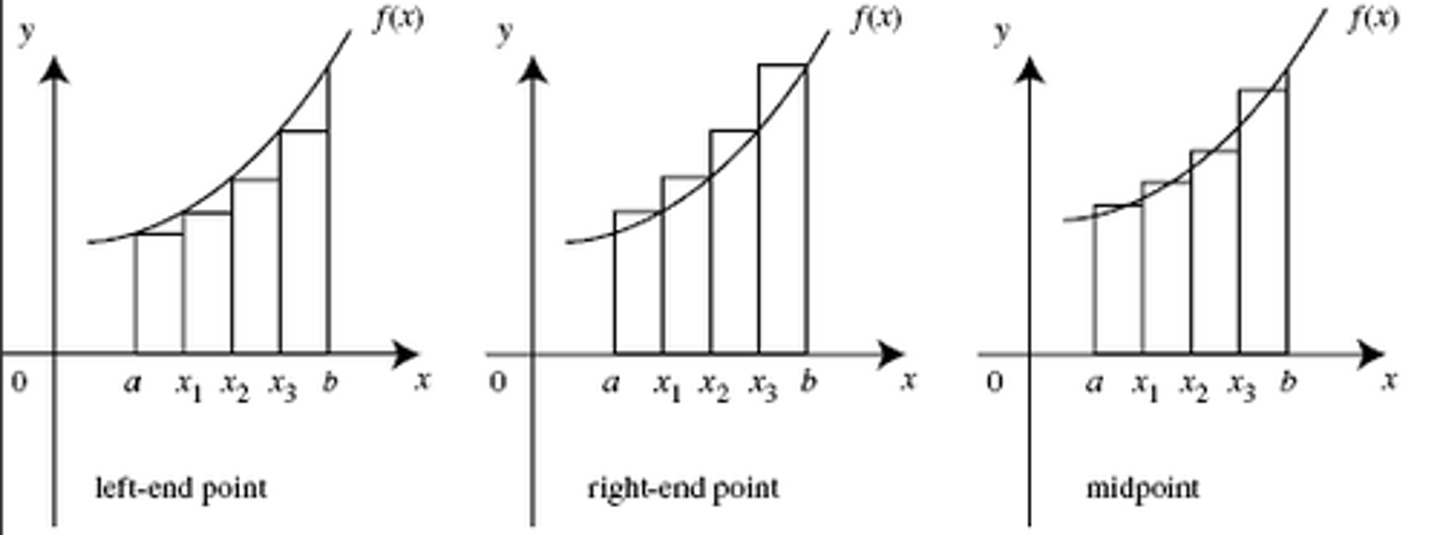
Midpoint Riemann Sum

midpoint of rectangle touches the curve.
length of interval*(all y values on curve that the midpoint of the rectangle touches)

area of each trapezoid

interval/2 * (b₁+b₂)

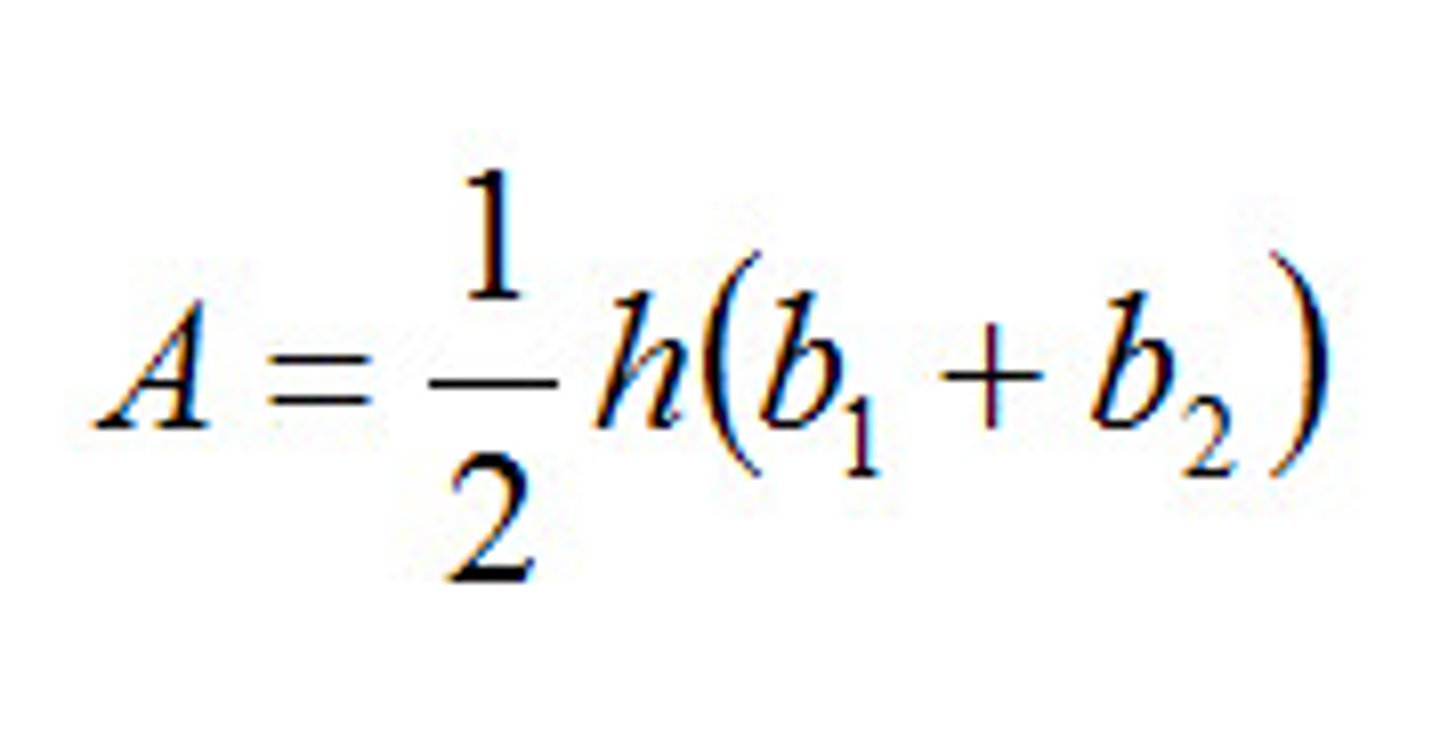
trapezoidal rule

use trapezoids to evaluate integrals (estimate area).
average of LRAM and RRAM.
(interval/2) * (y0 +2y1 + 2y2 + 2y3 ... + yn)

overestimates the integral where the graph is concave up, and underestimates the integral where the graph is concave down.

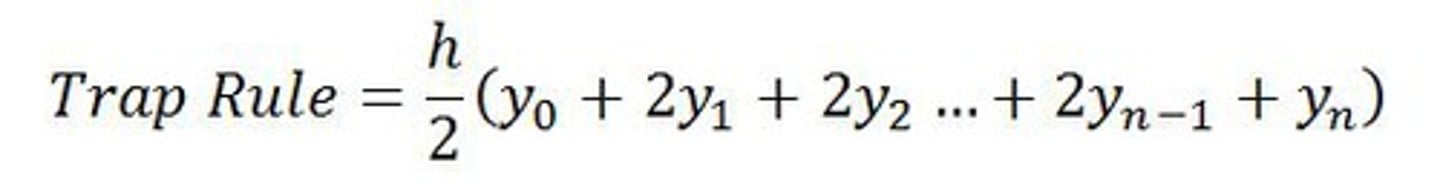
definite integral

has upper and lower bounds a & b. find antiderivative, F(b) - F(a)

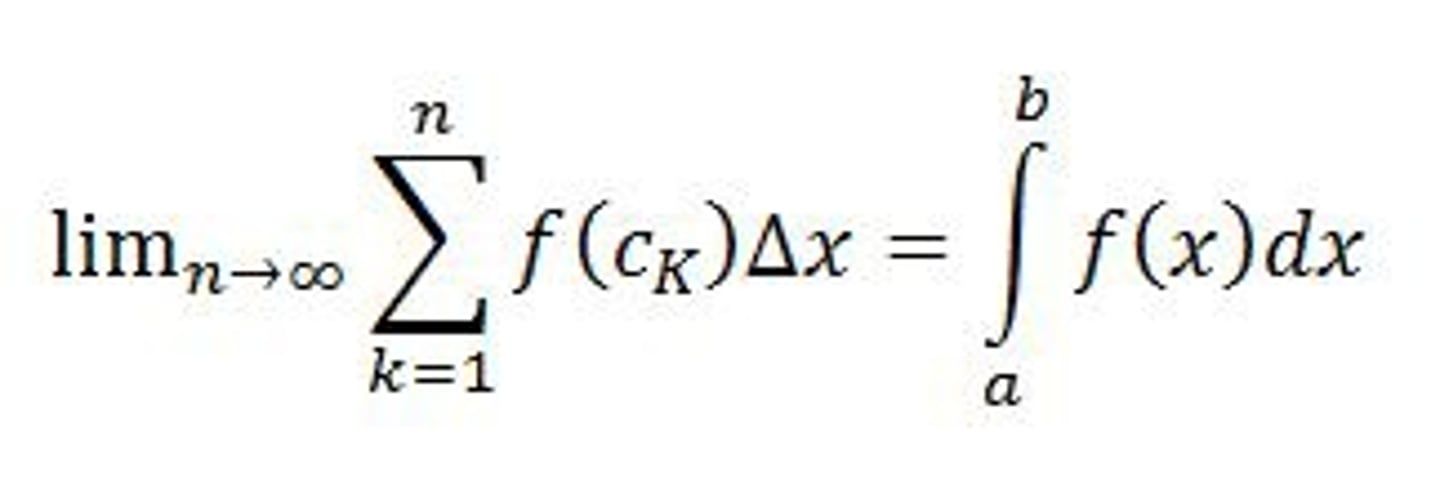
area under a curve

∫ f(x) dx
integrate over interval a to b

average value of f(x)

1/(b-a) * ∫ f(x) dx on the interval a to b

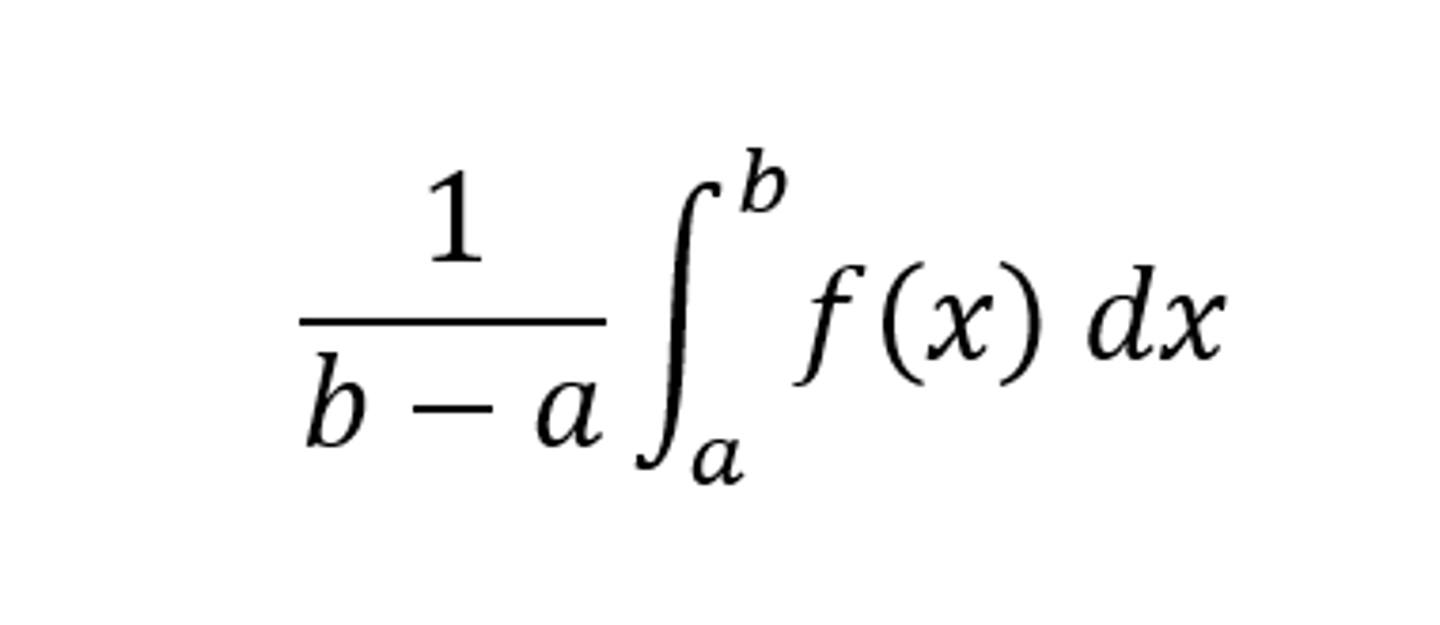
Mean Value Theorem for Definite Integrals

average value of integral = actual value. MUST check conditions (continuous on closed interval)

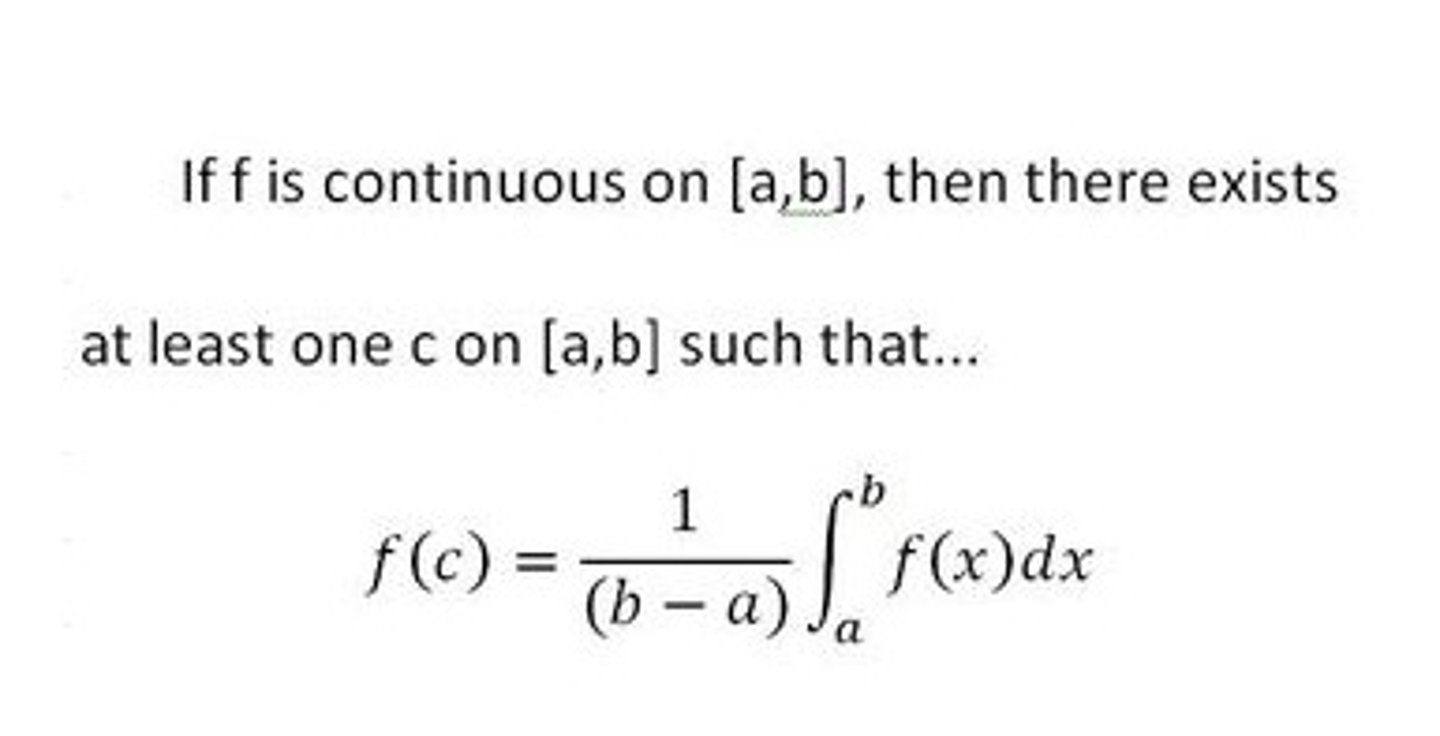
If g(x) = ∫ f(t) dt on the interval 2 to x, then g'(x) =

g'(x) = f(x)

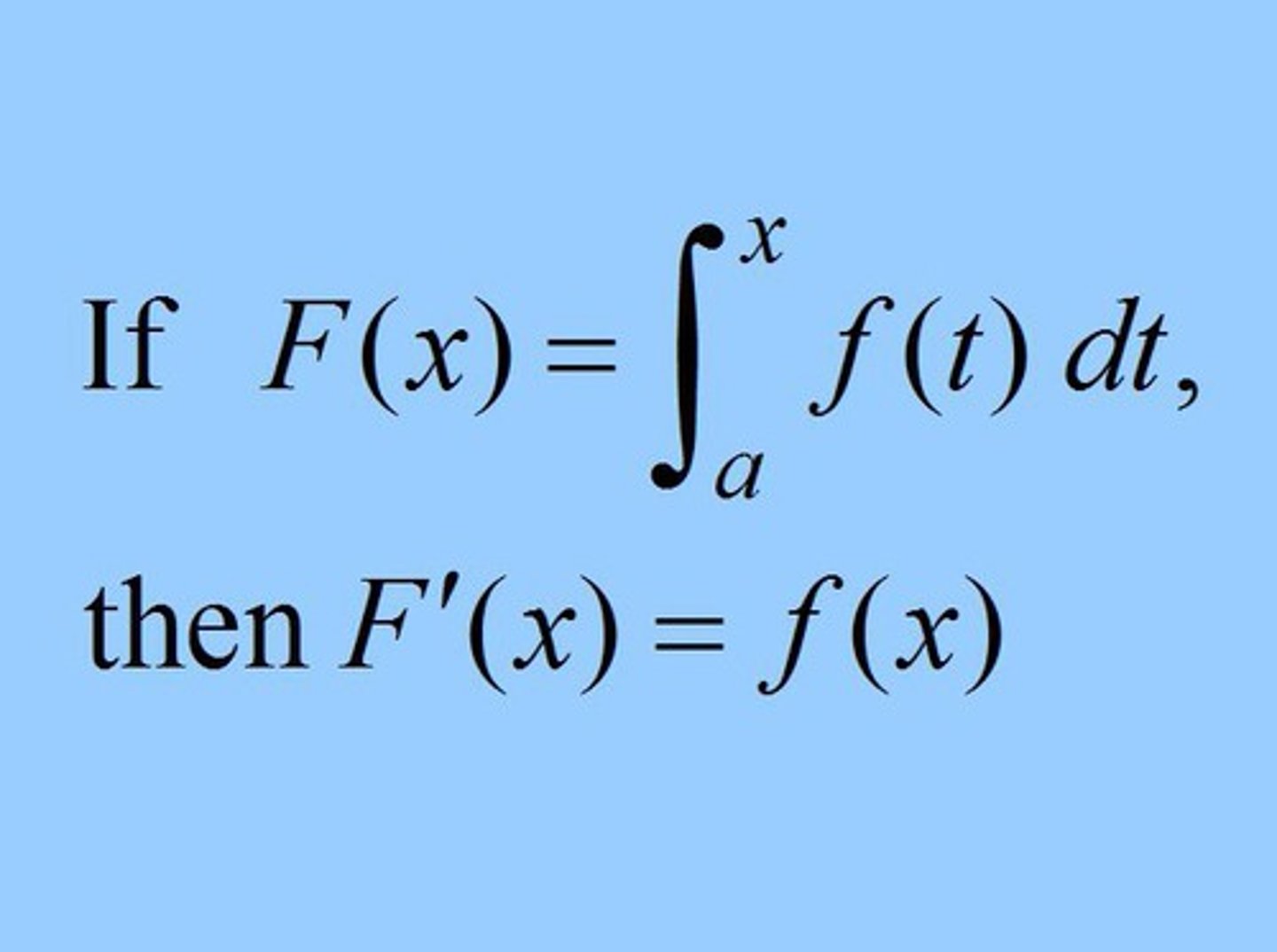
Fundamental Theorem of Calculus

∫ f(x) dx on interval a to b = F(b) - F(a).

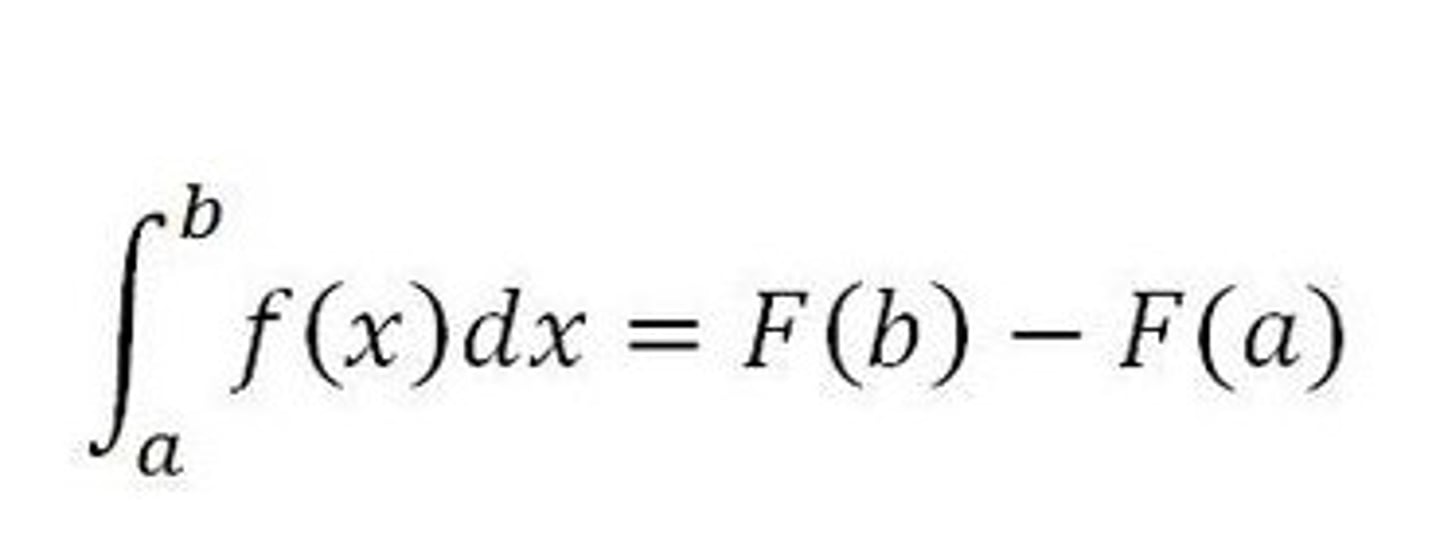
Fundamental Theorem of Calculus part 2

• variable in derivative (usually d/dx) matches the variable (upper bound) in the integral symbol
• lower limit is a constant, upper limit is a variable
• we have an integral and a derivative

Integration by parts formula

∫u dv= uv-∫vdu

u= use LIPET
dv= rest of integrand given

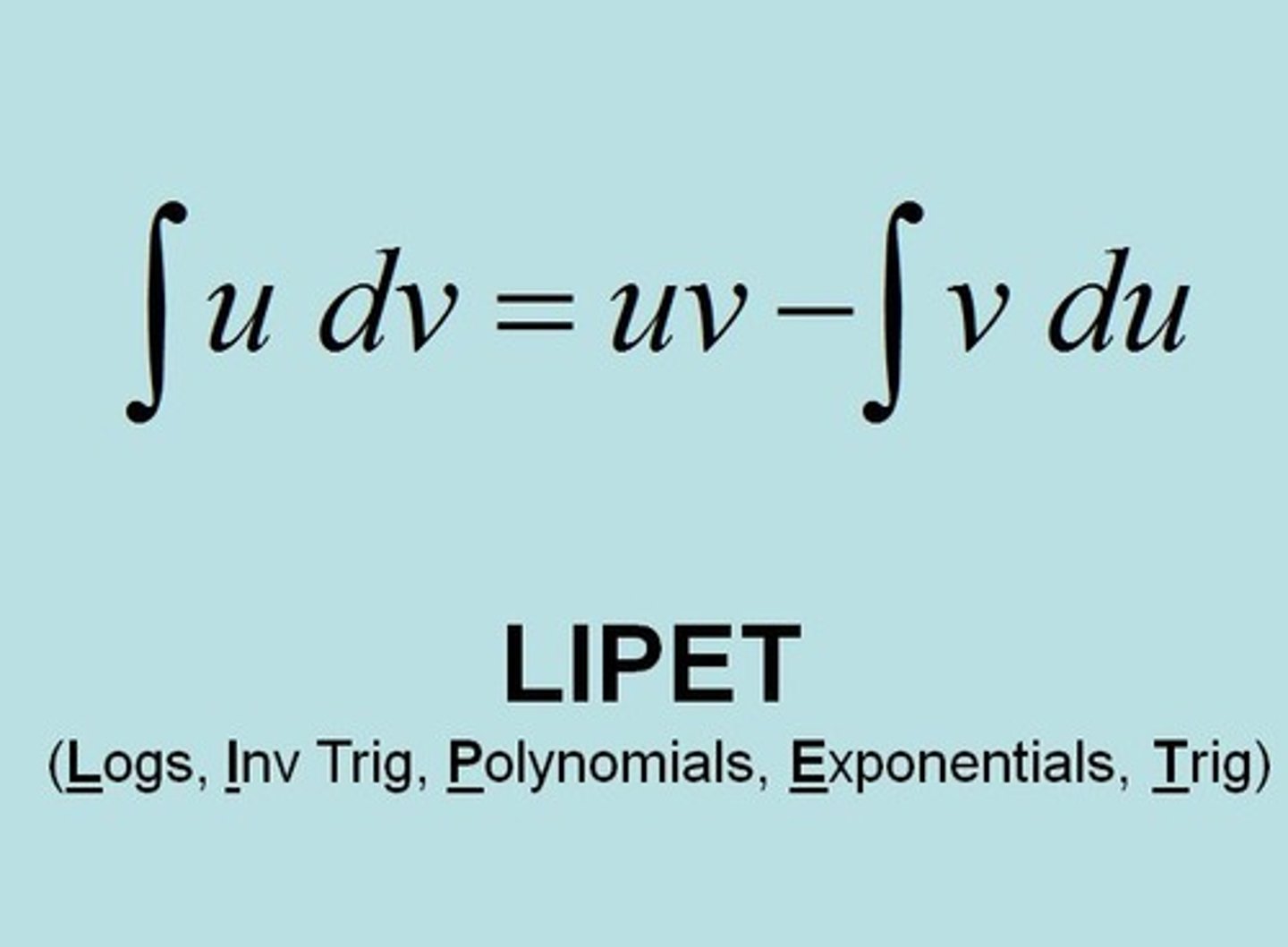
exponential growth equation

k= constant of proportionality.

used if y changes at a rate proportional to the amount present

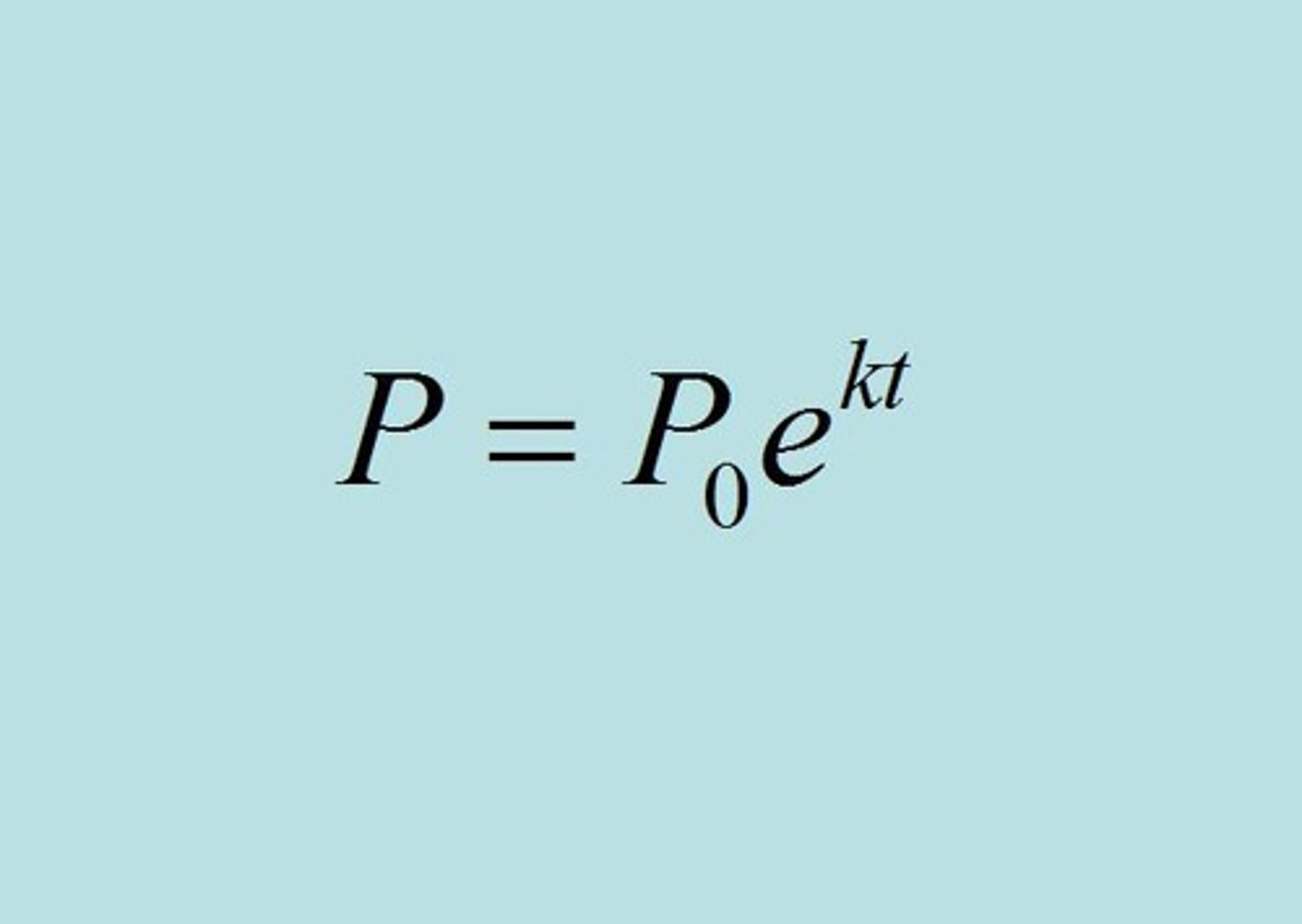
exponential differential equation

dP/dt= kP

logistic growth equation

P = M / (1 + Ae^(-Mkt))

M= carrying capacity
k= growth constant
A= a constant

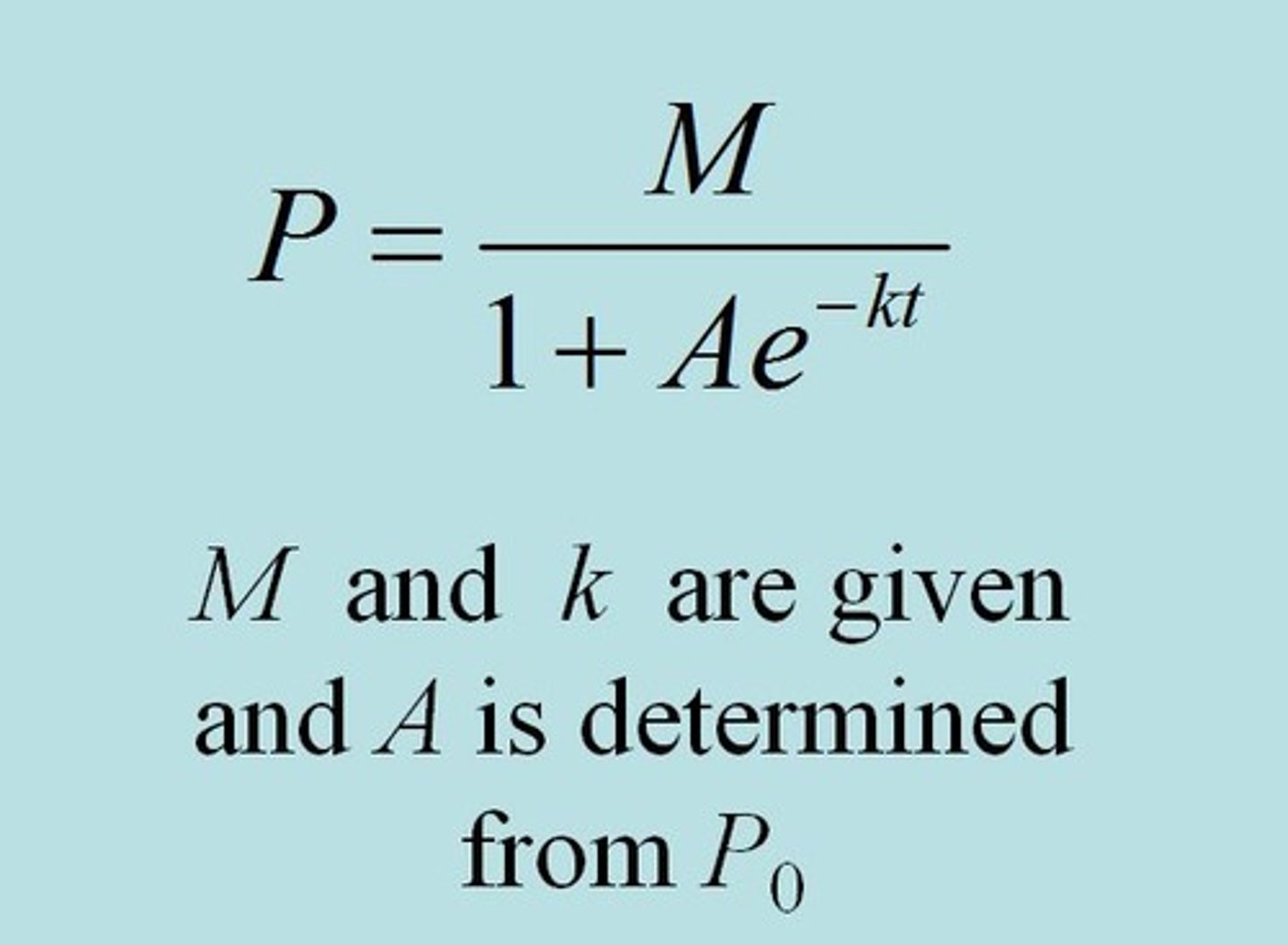
logistic differential equation

2 logistic differential equations:

dP/dt = kP(M - P)

AND

dP/dt = kP(1-P/M)

M = carrying capacity
k= proportionality constant
P= population

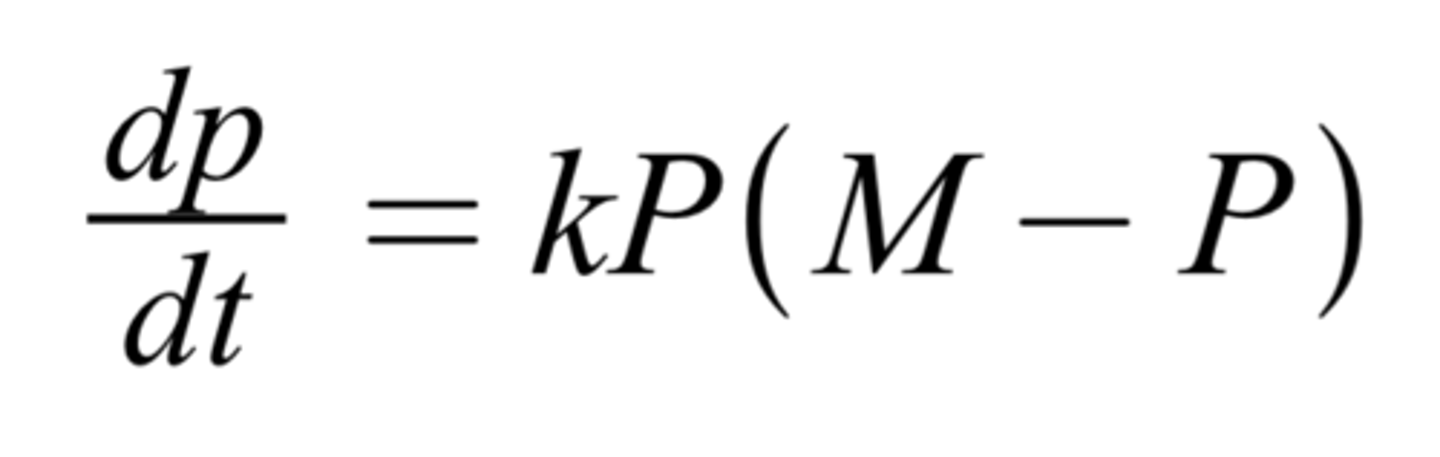
Taylor series of arctan(x)

ALL TRIG EQUATIONS= positive, negative, positive, negative WITH A (-1)ⁿ

arctan does NOT have a factorial in the denominator. exponent matches denominator. arctan has all odd exponents


x^2n+1 / 2n+1

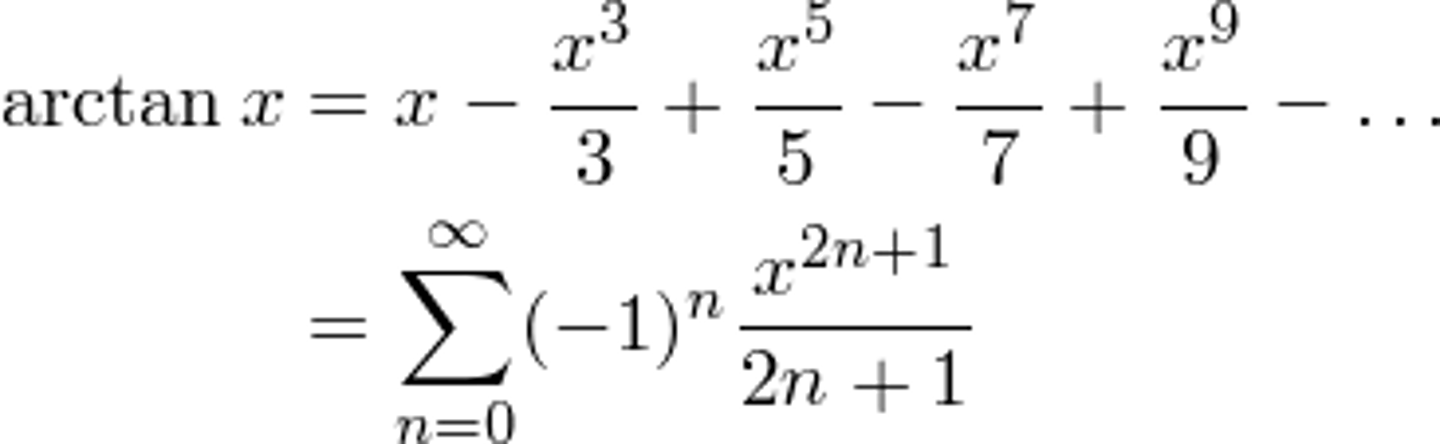
taylor series for (1+x)^k

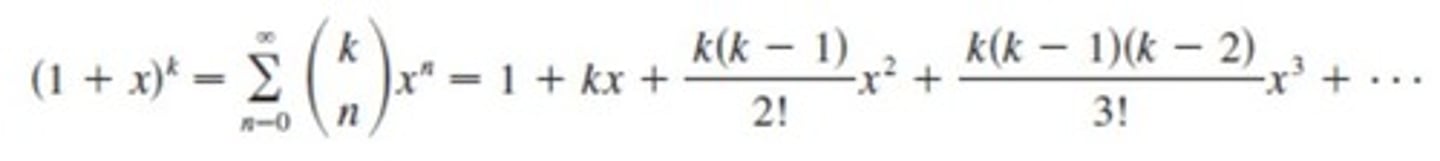
given rate equation, R(t) and initial condition when
t = a and R(t) = y₁, find final value when t = b

y₁ + Δy = y
original rate + change in rate = new rate
Δy = ∫ R(t) over interval a to b

given v(t) and initial position t = a, find final position when t = b

s₁+ Δs = s
original position + change in position = new position
Δs = ∫ v(t) over interval a to b

given v(t) find displacement

∫ v(t) over interval a to b

given v(t) find total distance travelled

∫ |v(t)| over interval a to b

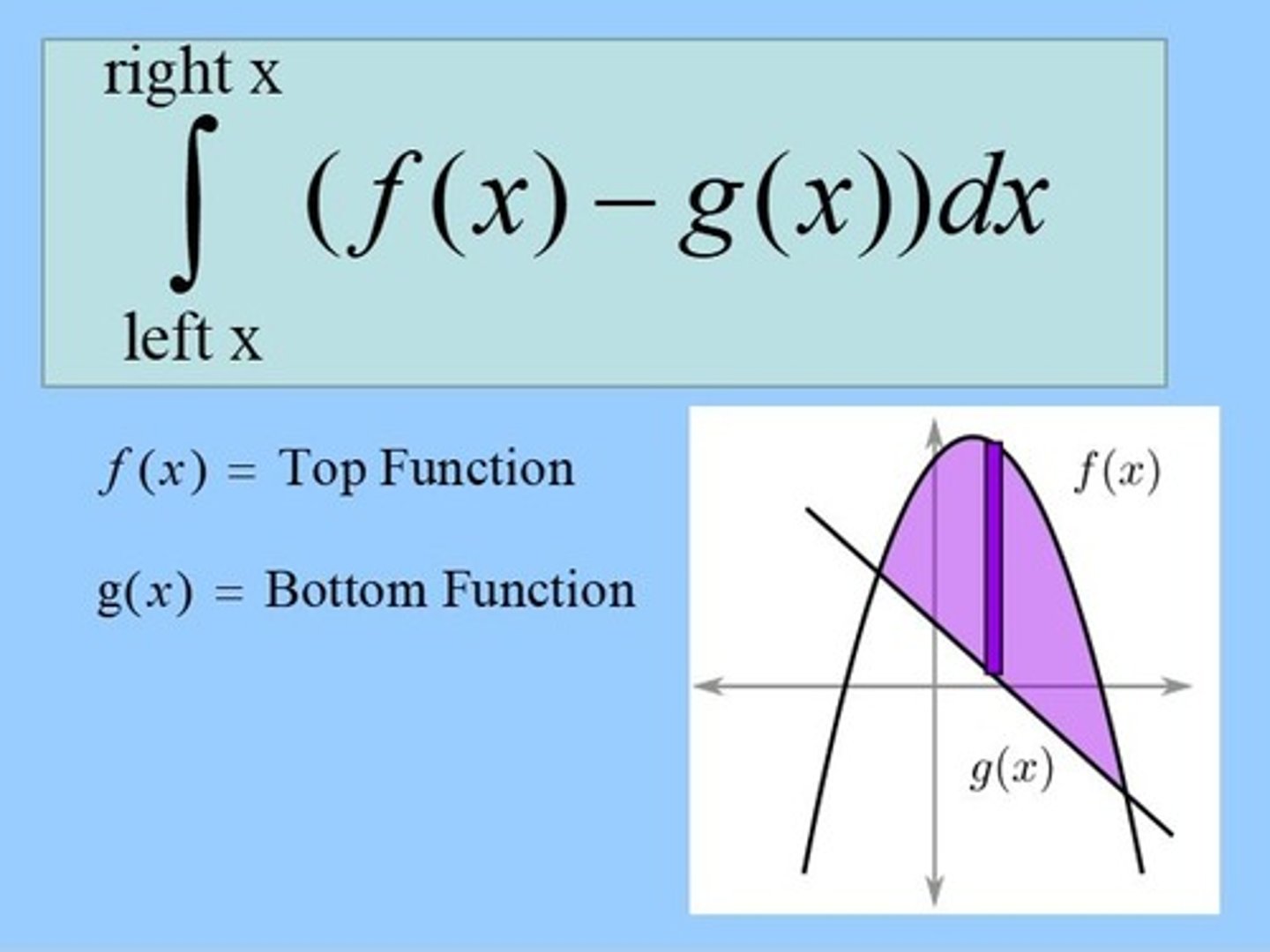
area between two curves (dx)

∫ f(x) - g(x) over interval a to b

f(x) is top function and
g(x) is bottom function
(dx: vertical strips)

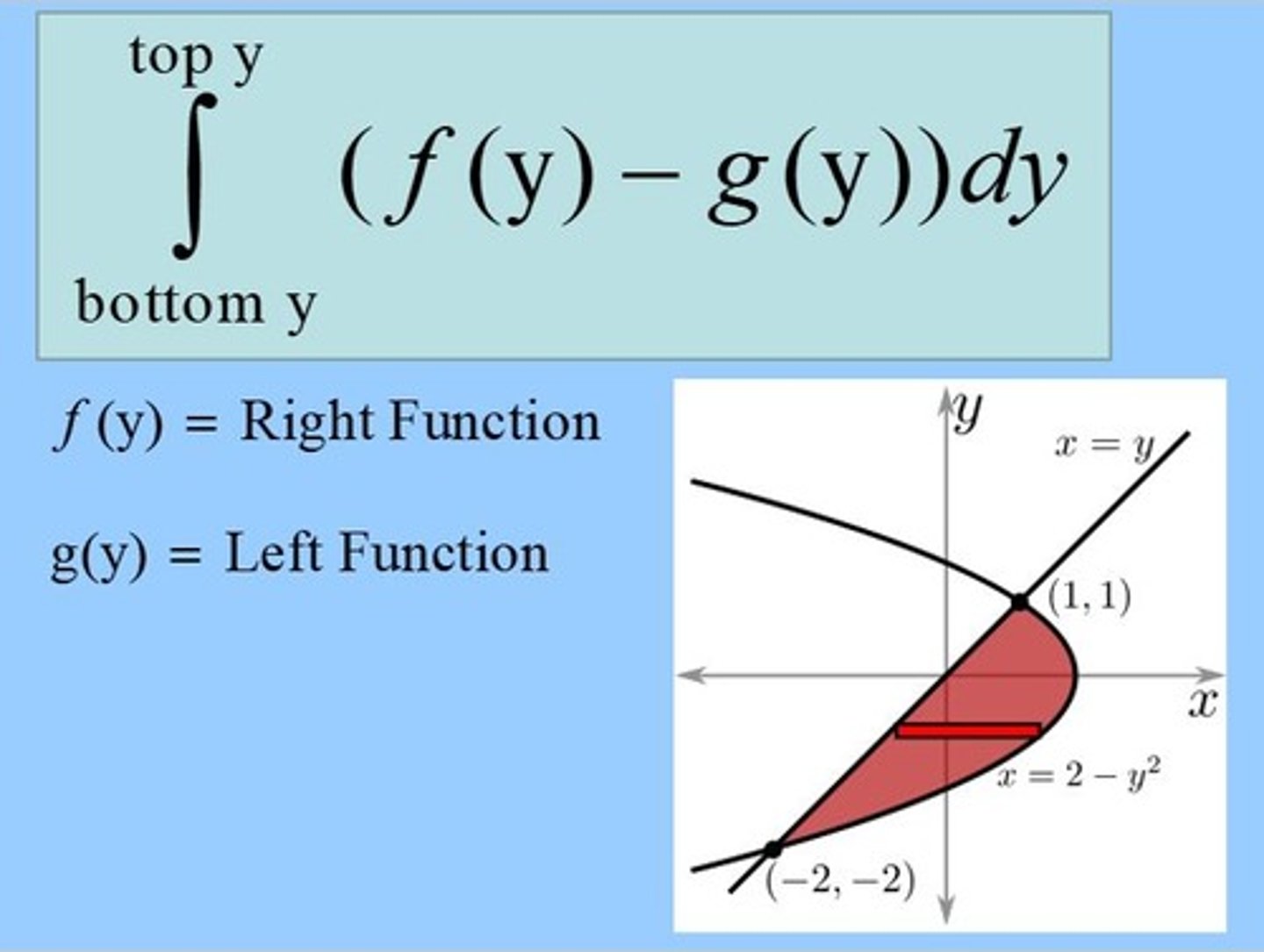
area between two curves (dy)

dy= horizontal strips bc width of horizontal strip=dy

∫ f(x) - g(x) over interval a to b

f(x) is right function and
g(x) is left function

1. solve the equations to be x=, so you can have it in terms of dy
2. find y values of intersections (these will be bounds for integral)
3. subtract RIGHT - LEFT functions

volume of solid with base in the plane and given cross-section

∫ A(x) dx over interval a to b
A(x) = the area of the given cross-section shape as a function of x

volume of solid of revolution - disks

π ∫ r² dx over interval a to b

r = distance from curve to axis of revolution

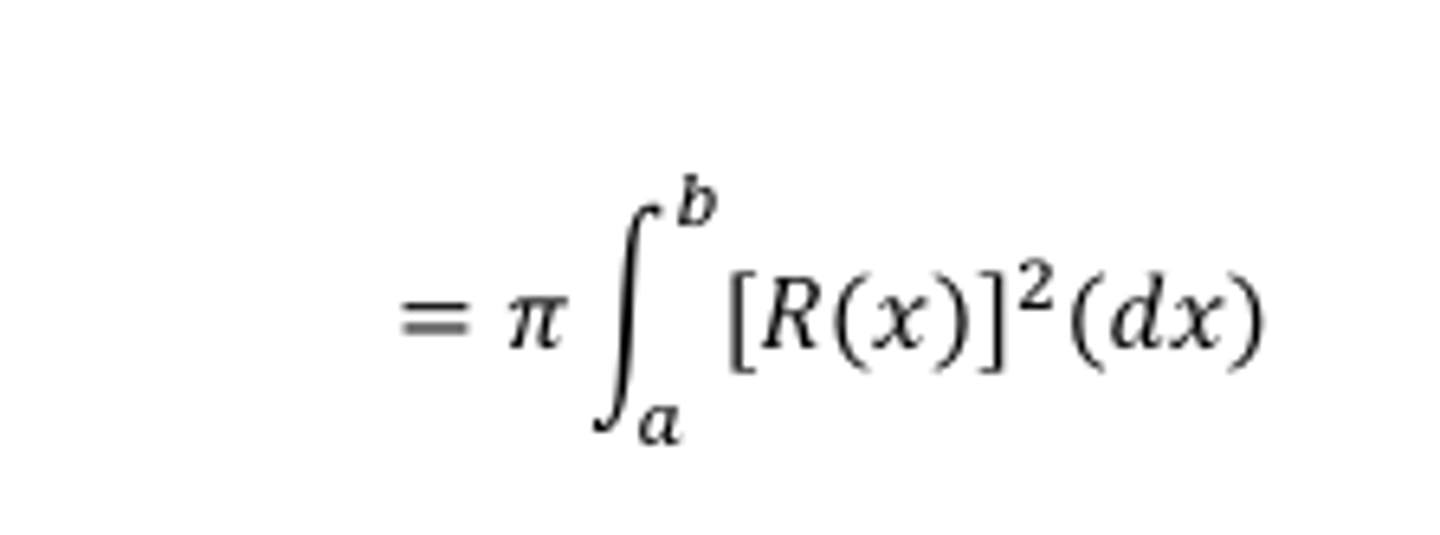
volume of solid of revolution - washers

π ∫ R² - r² dx over interval a to b

R = farthest distance from outside curve to axis of revolution,
r = closest distance from inside curve to axis of revolution

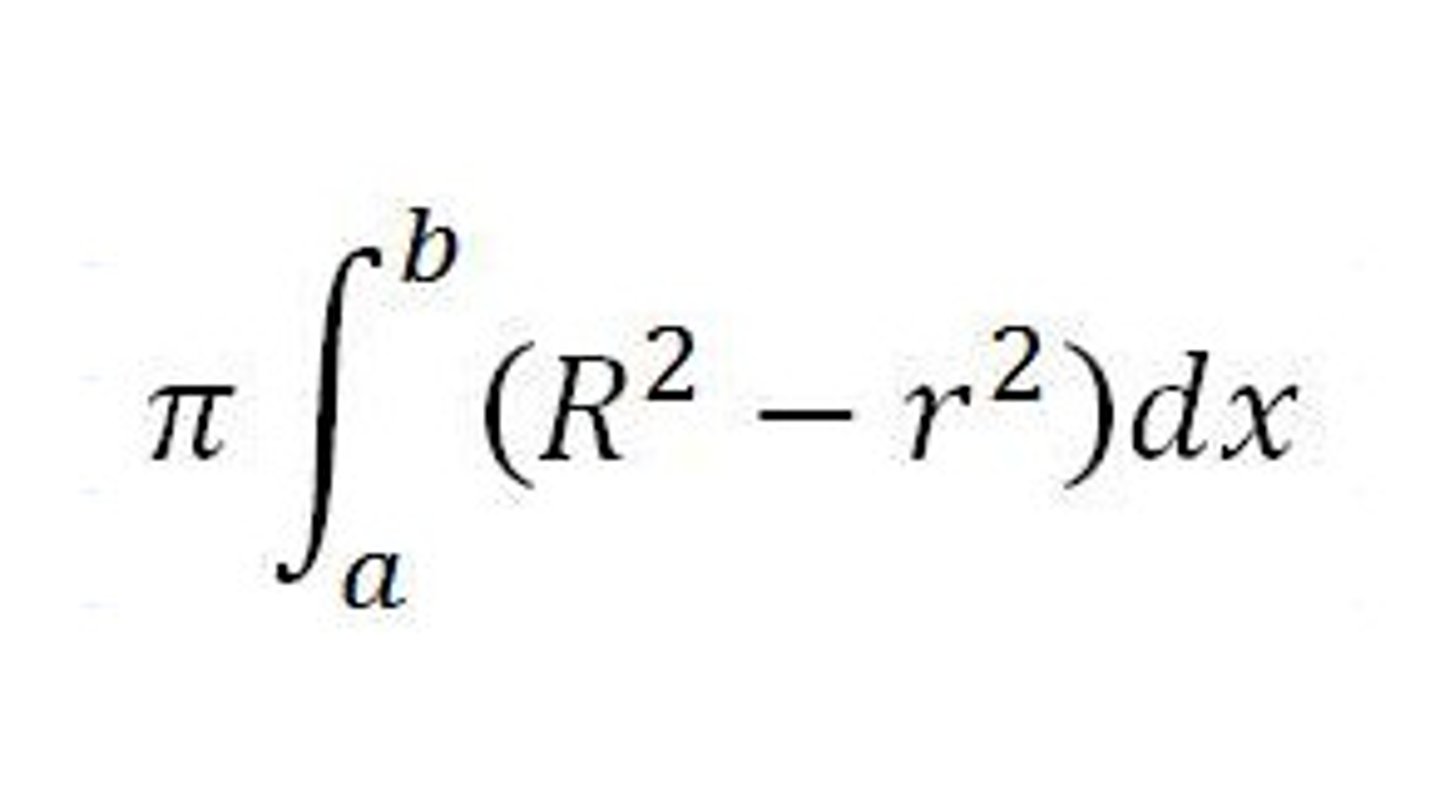
Shells Method

V= 2π ∫R(x) * h(x) dx

length of curve for rectangular functions

∫ √(1 + (dy/dx)²) dx over interval a to b

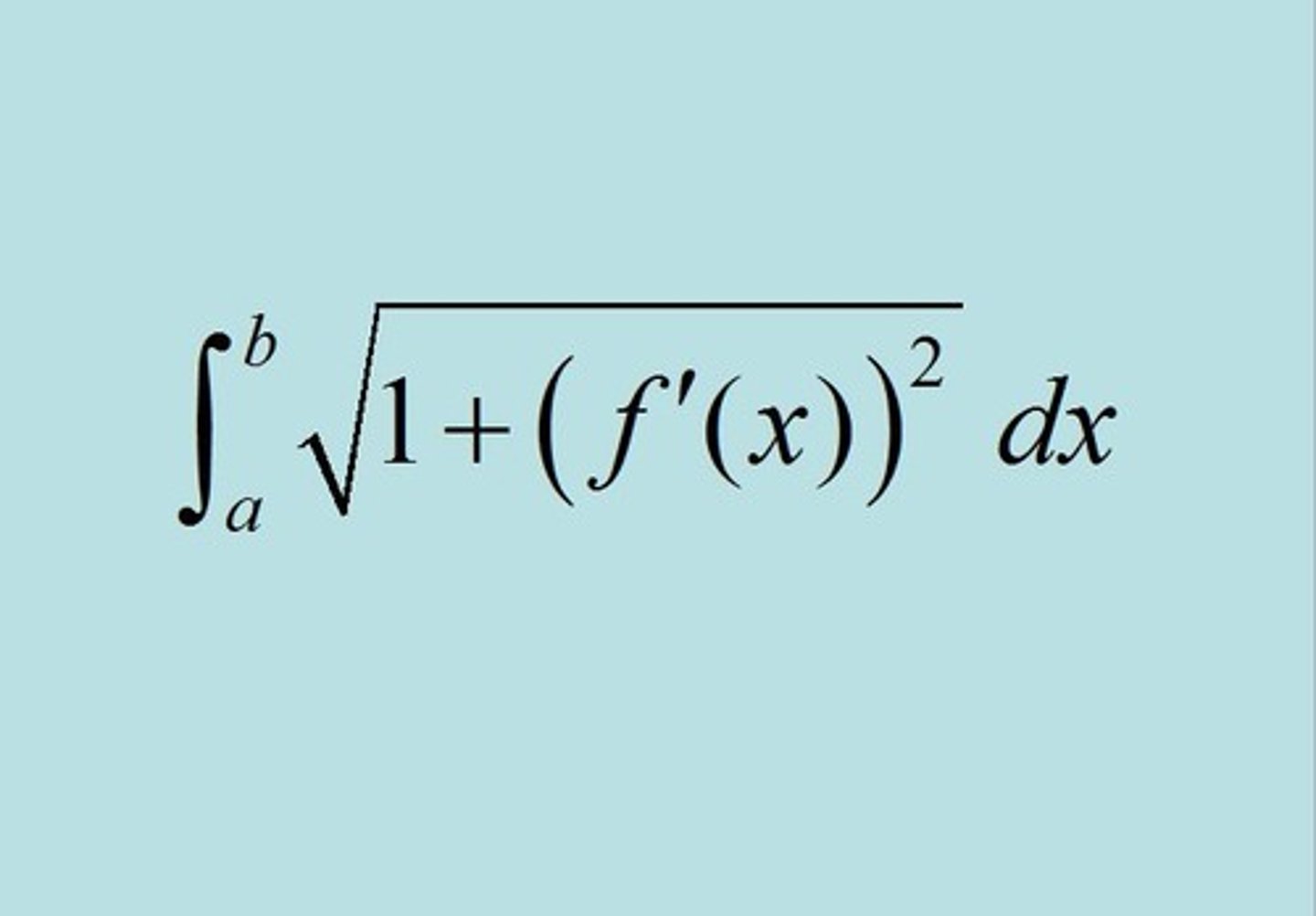
L'Hopitals rule

used to find limits when substitution gives you 0/0 or ∞/∞

find derivative of numerator and denominator separately, then evaluate limit

alternating series test

used on series that alternate from pos-> neg

if the lim as n->∞ of aₙ = 0, and the terms decrease, then the series converges

Nth Term Test for Divergence

if terms grow without bound (if lim as x->∞ ≠ 0 or DNE), series diverges

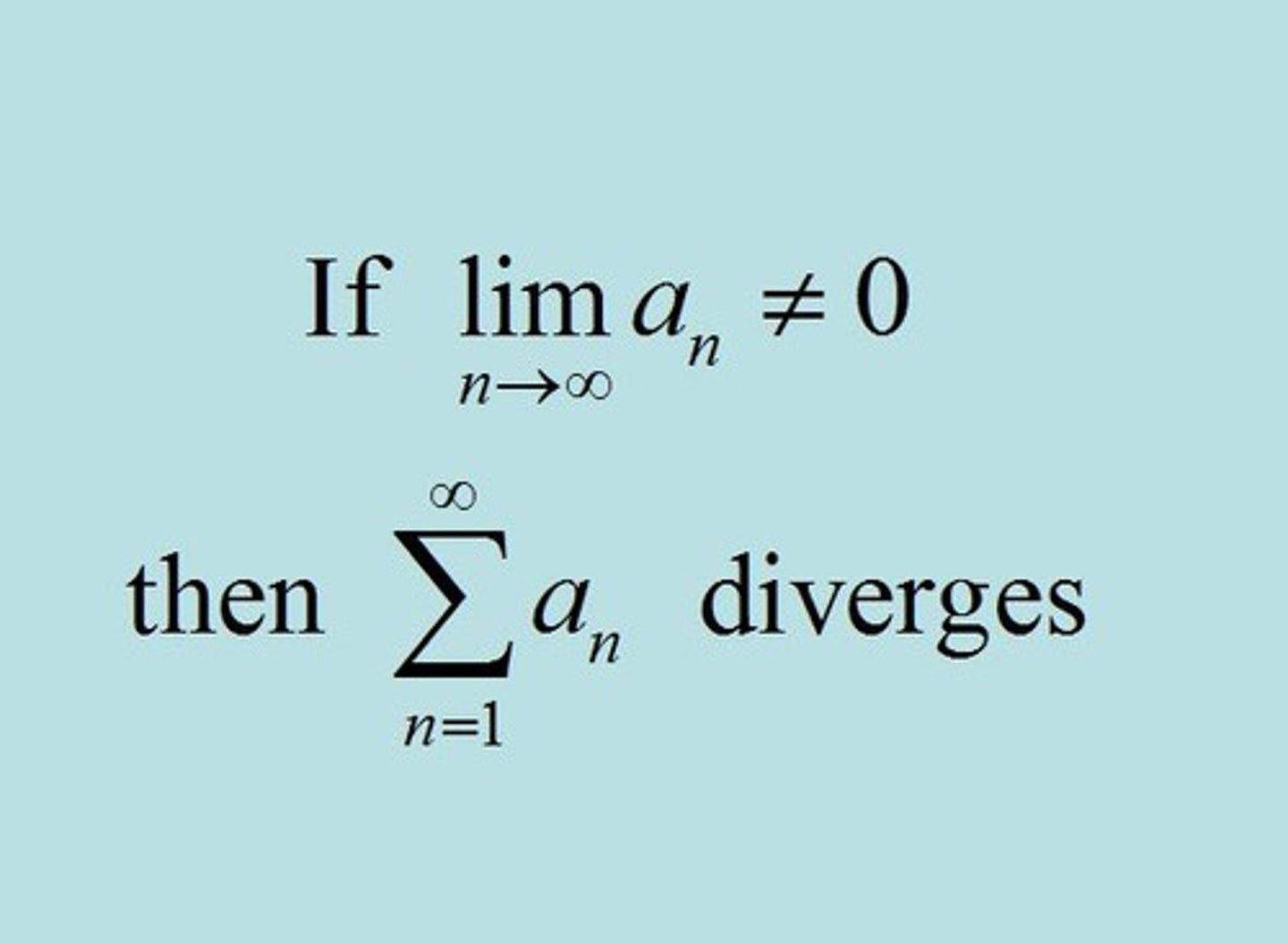
Ratio Test

lim as n-> ∞ of | a(n+1) / aₙ term | = L

lim as n-> ∞ of absolute value of n+1 term divided by n term.

L < 1, series converges
L = 1, inconclusive
L > 1, series diverges

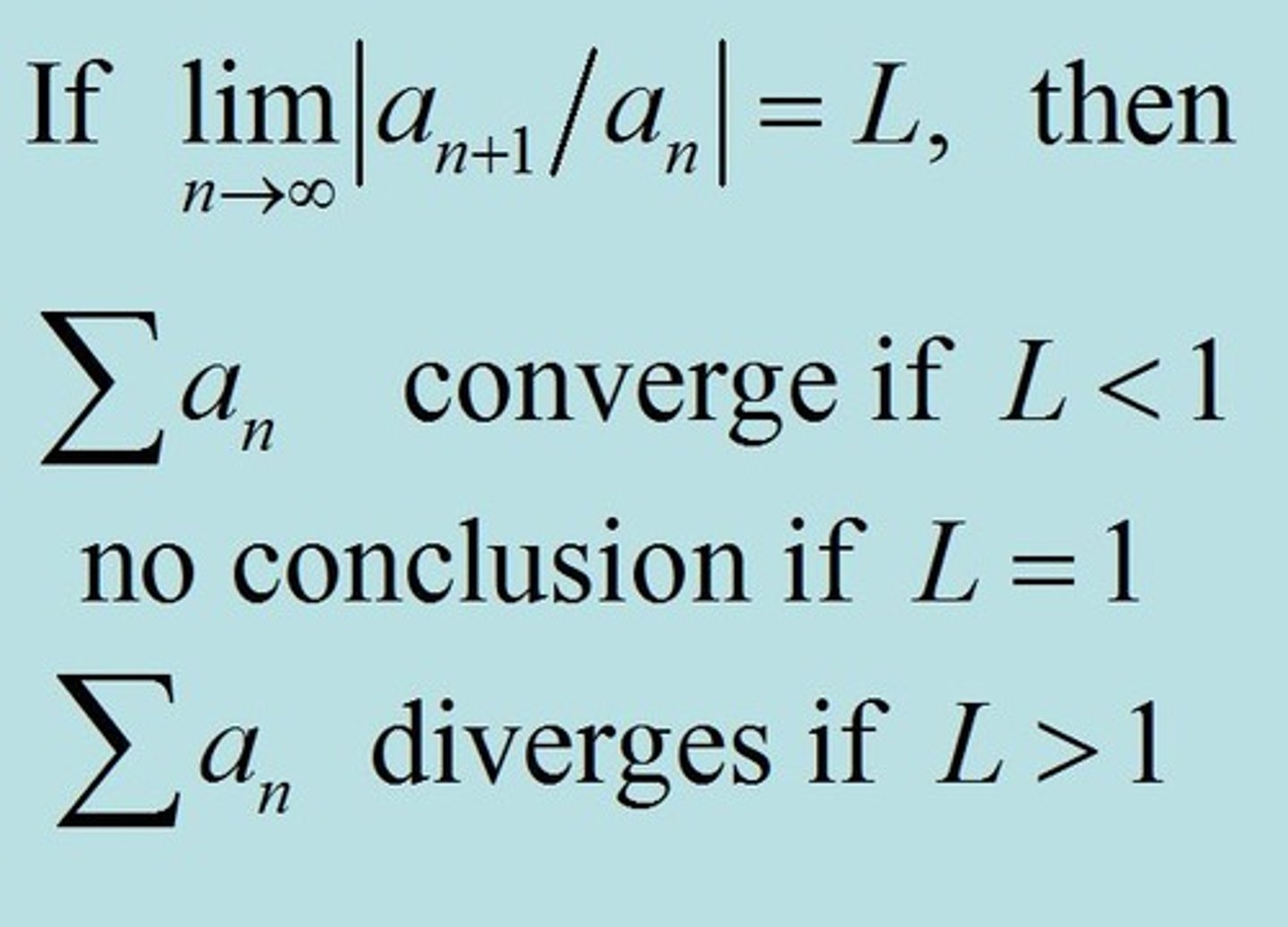
nth root test

lim as n-> ∞ of ⁿ√|aₙ| = L

lim as n-> ∞ of the nth root of the absolute value of a series = L

L < 1, series converges
L = 1, inconclusive
L > 1, series diverges

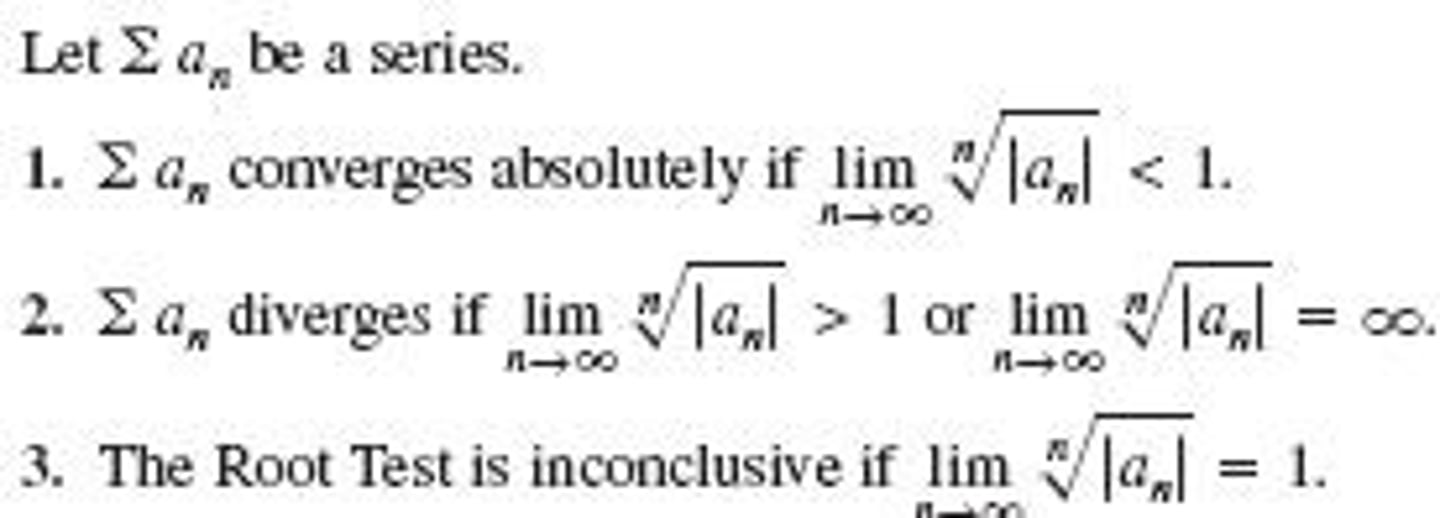
integral test

aₙ is a positive and decreasing series.

then, ∑aₙ and ∫aₙ both converge or diverge

the integral and series both converge or both diverge. DOES NOT necessarily converge to the number you get.

Direct Comparison Test

ONLY for series with all positive terms
Given two series:
if "bigger" series converges, both converge
if "smaller" series diverges, both diverge

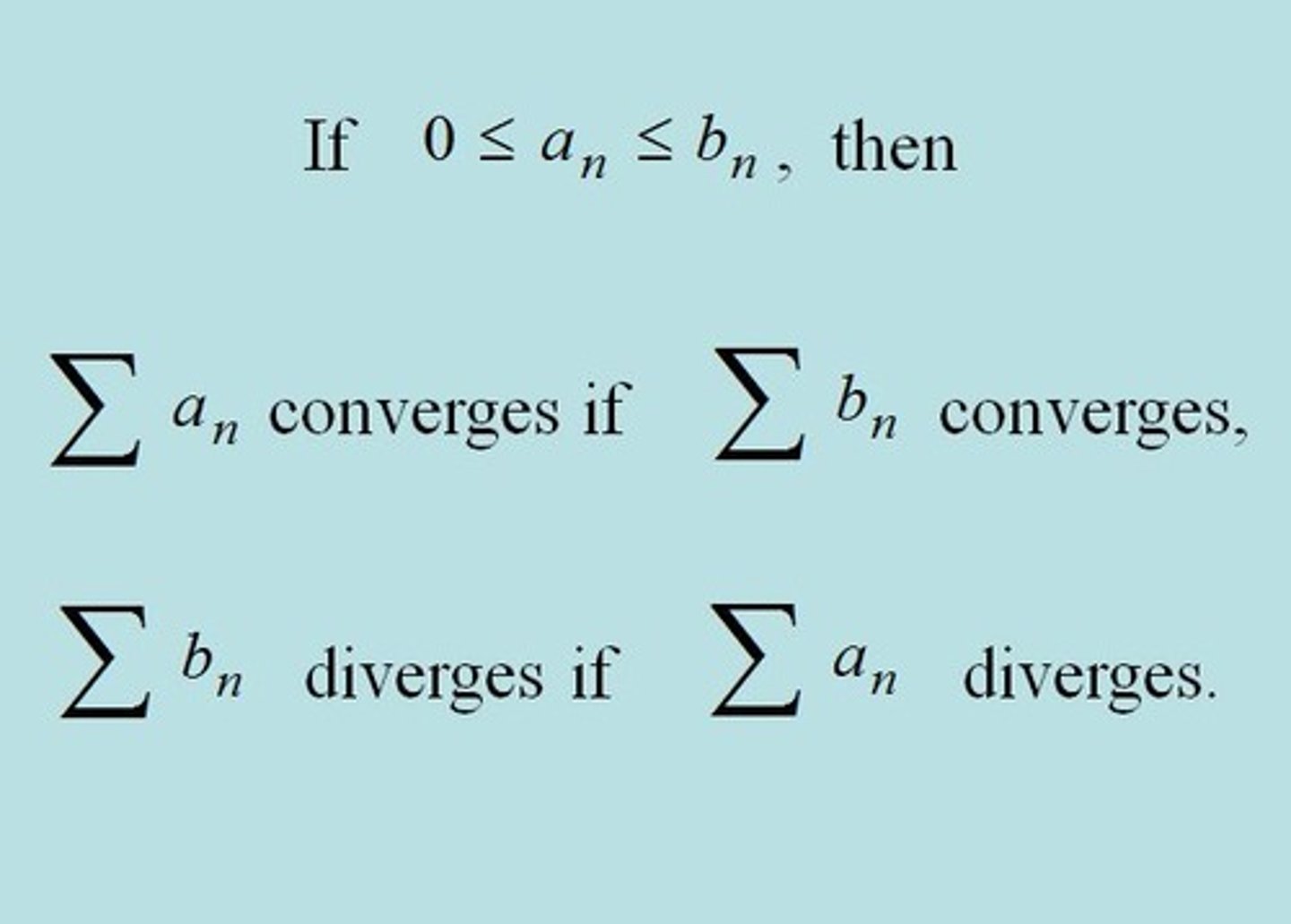
limit comparison test

if the lim as n approaches ∞, of the ratio of aₙ/bₙ, is a positive integer, then both series will converge or diverge

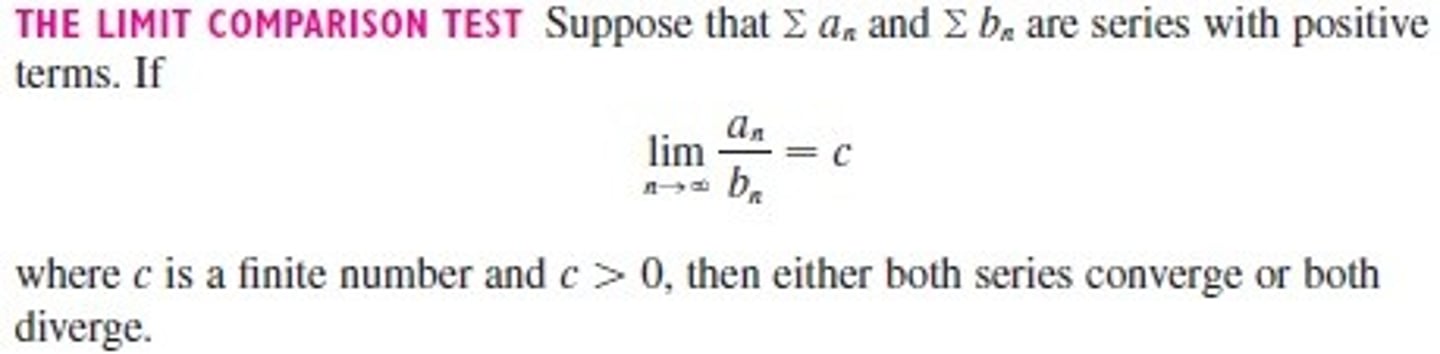
Absolute Convergence Test

if a series aₙ has NEGATIVE terms, use absolute convergence test to test for absolute convergence

if ∑ |aₙ| converges, then ∑ aₙ converges absolutely.
if a series converges absolutely, it converges.

sooo if ∑ |aₙ| converges, then ∑ aₙ converges

(if the absolute values of a series converges, the original series converges too)

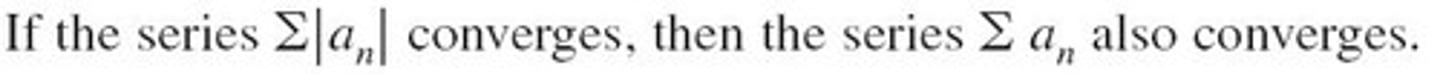
geometric series test

general term = a₁r^n
converges if -1 < r < 1, also known as |r| < 1 converges to a/1-r

|r| ≥ 1 diverges

p-series test

general term = 1/n^p, converges if p > 1
diverges if p ≤ 1

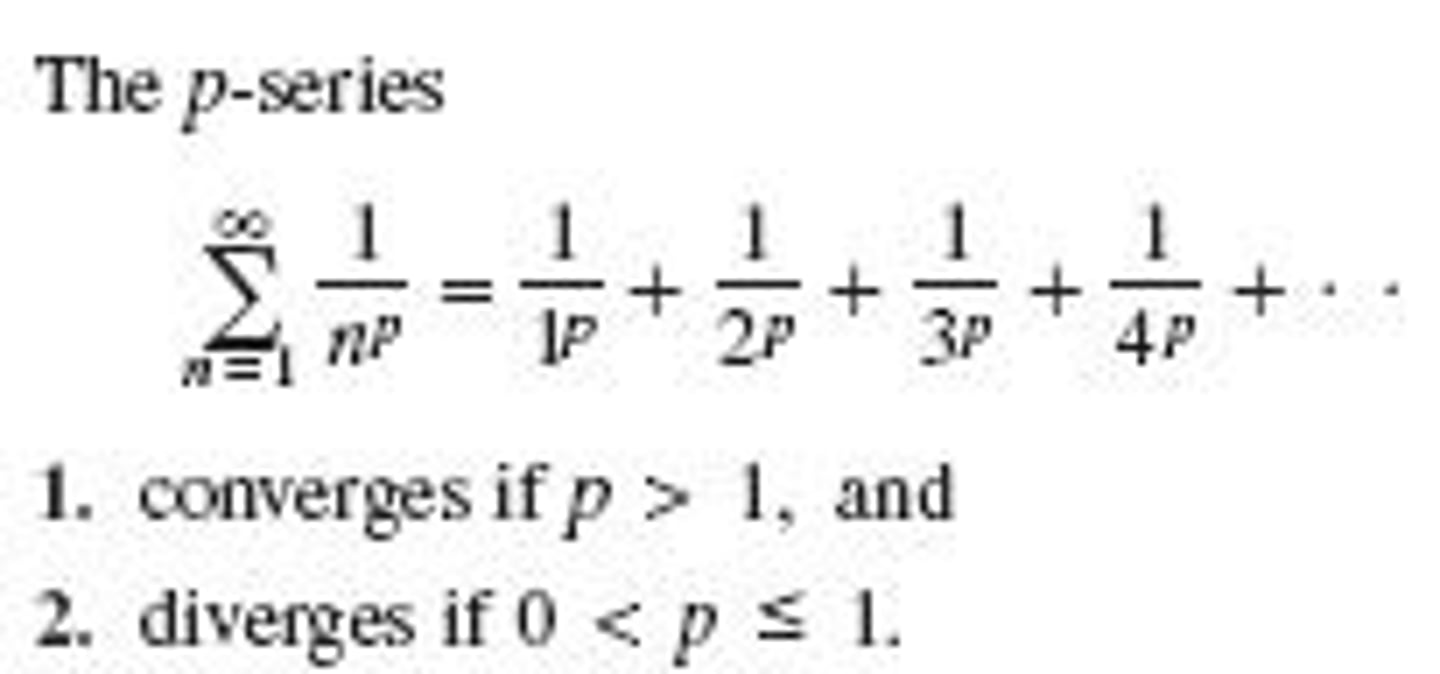
derivative of parametric curve

dy/dx = dy/dt / dx/dt

remember it's cancelling out dt

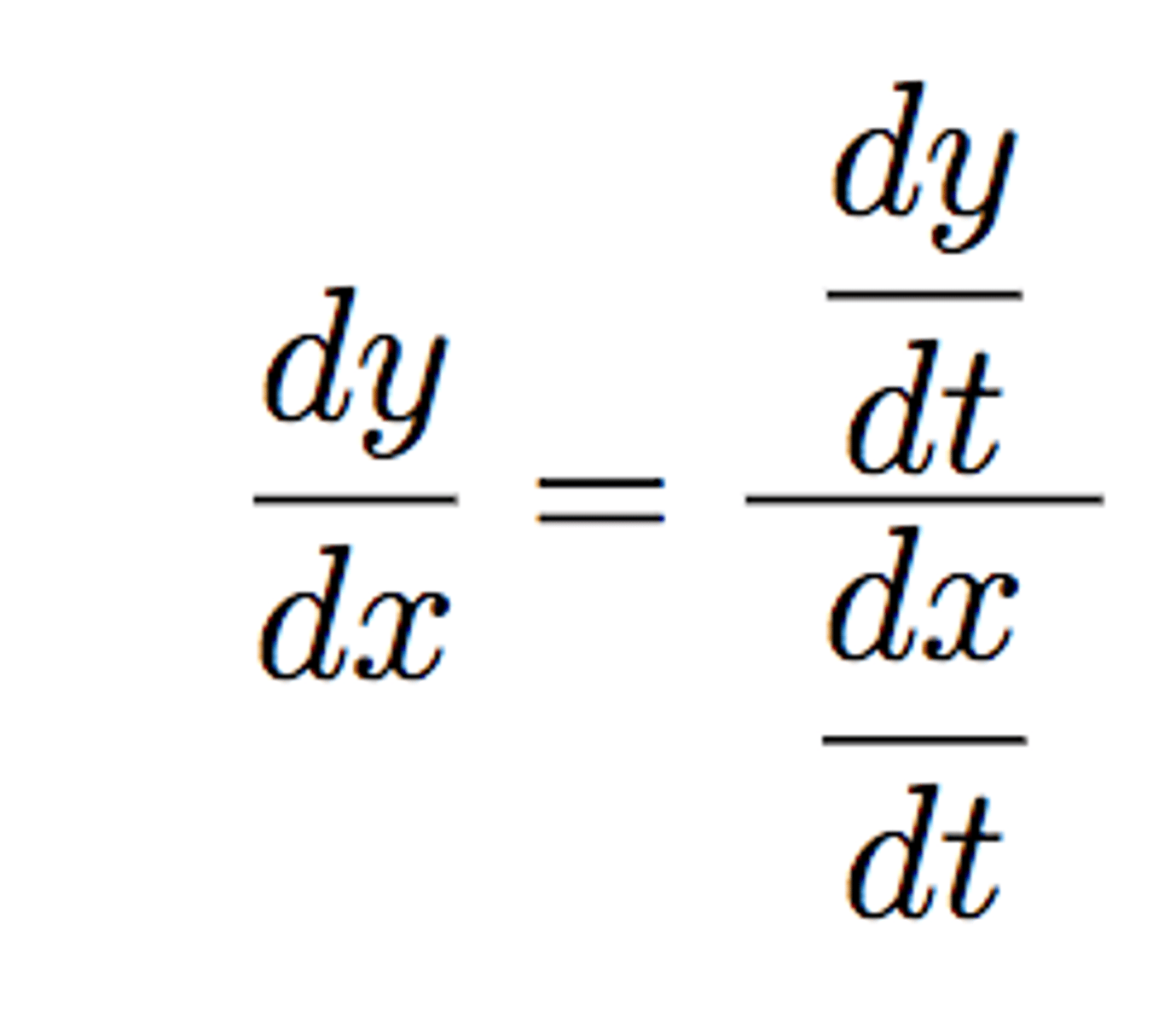
second derivative of parametric curve = d²y/dx²

d²y/dx²= dy'/dt / dx/dt
second derivative = first derivative divided by x'(t)

find first derivative, dy/dx = dy/dt / dx/dt.
then find the derivative of that by using the quotient rule.
now, divide by dx/dt

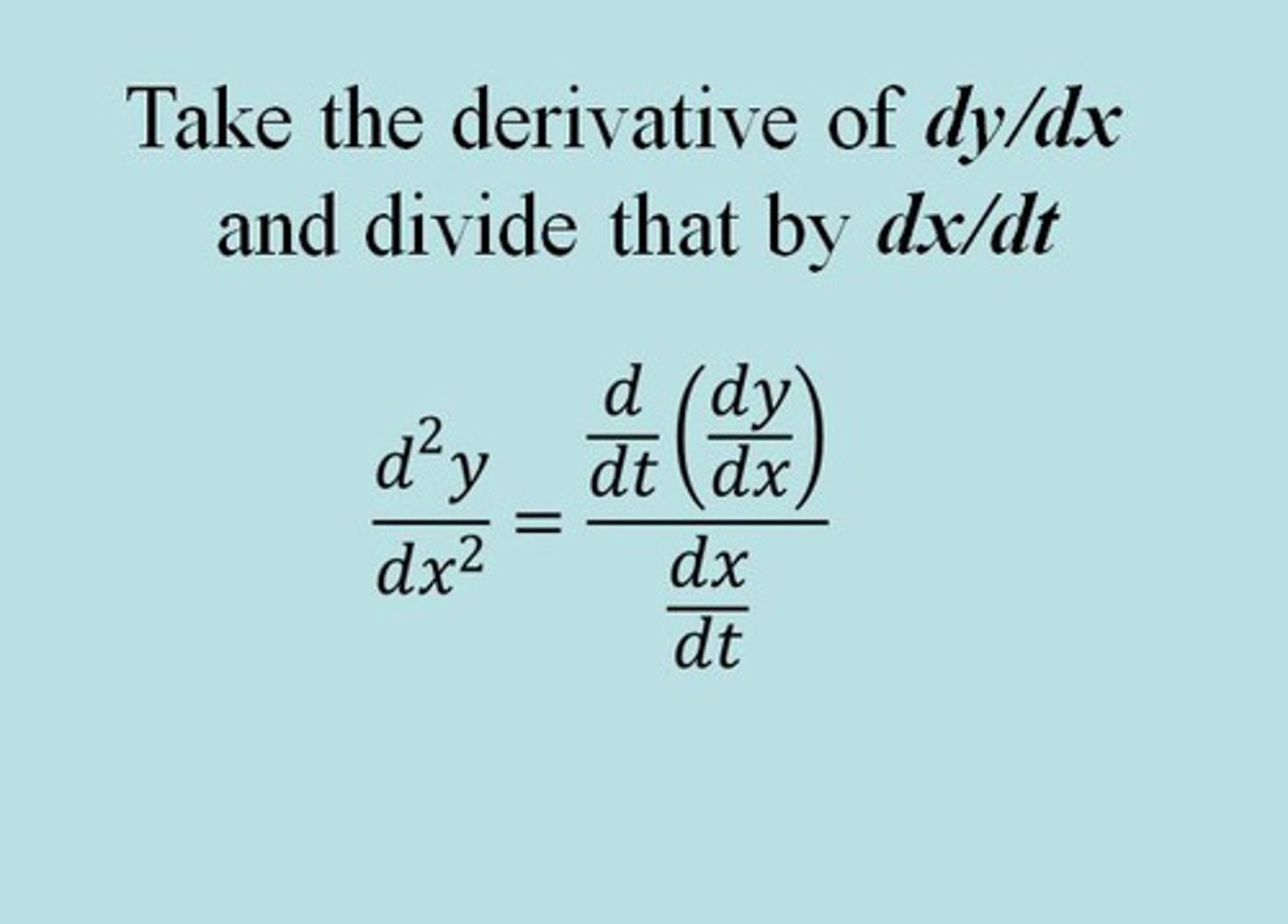
length of parametric curve

∫ √ (dx/dt)² + (dy/dt)² over interval from a to b

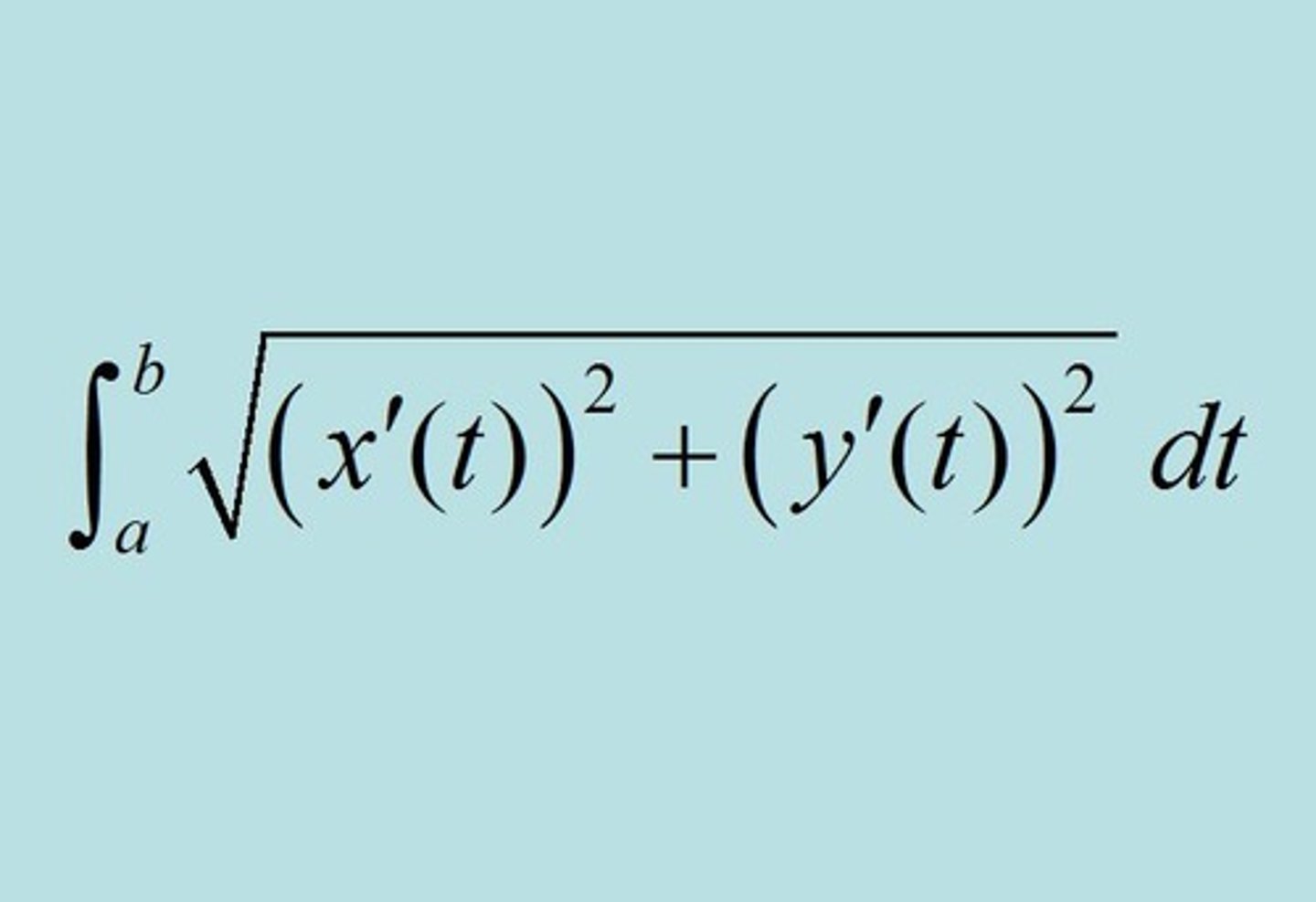
conversion from polar to rectangular coordinates

x= rcosθ
y= rsinθ

r²=x²+y²

derivative of a polar curve

take derivative of numerator and denominator separately by product rule:
dy/dx = == d/dθ rsinθ /// d/dθ rcosθ
=
r'sinθ + rcosθ // r'cosθ - rsinθ

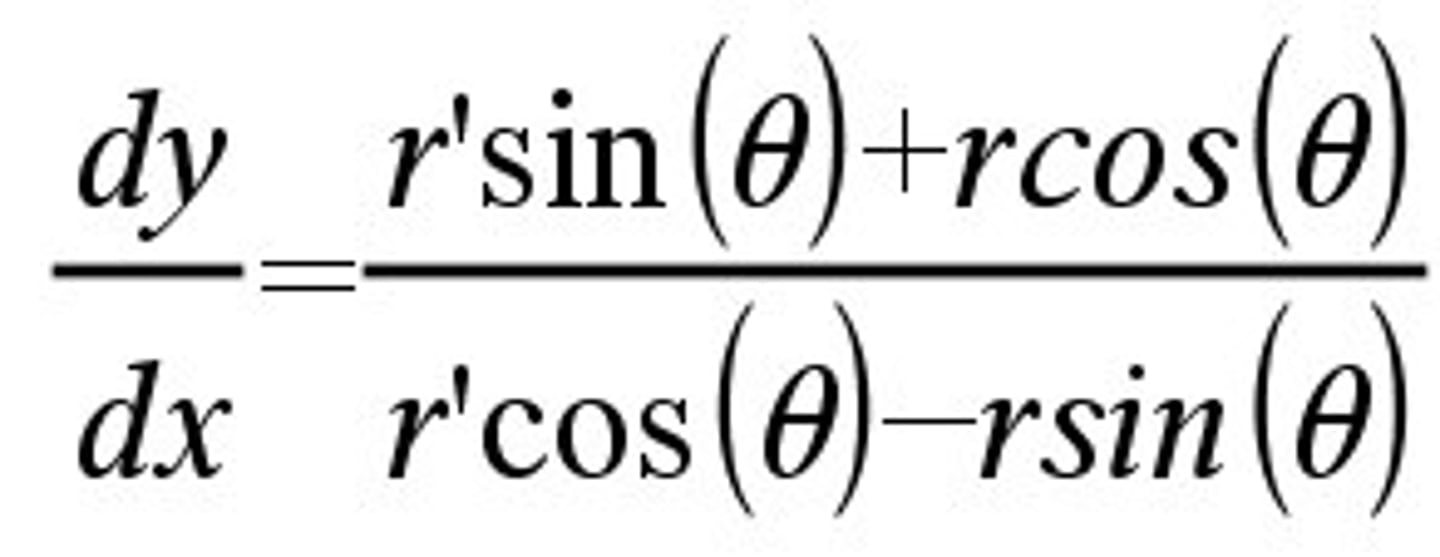
area inside 1 polar curve

1/2 ∫ r² over interval from a to b,
find α and β by setting r = 0, then solve for θ.

how to use:
theyll give r, so just sub into eq.

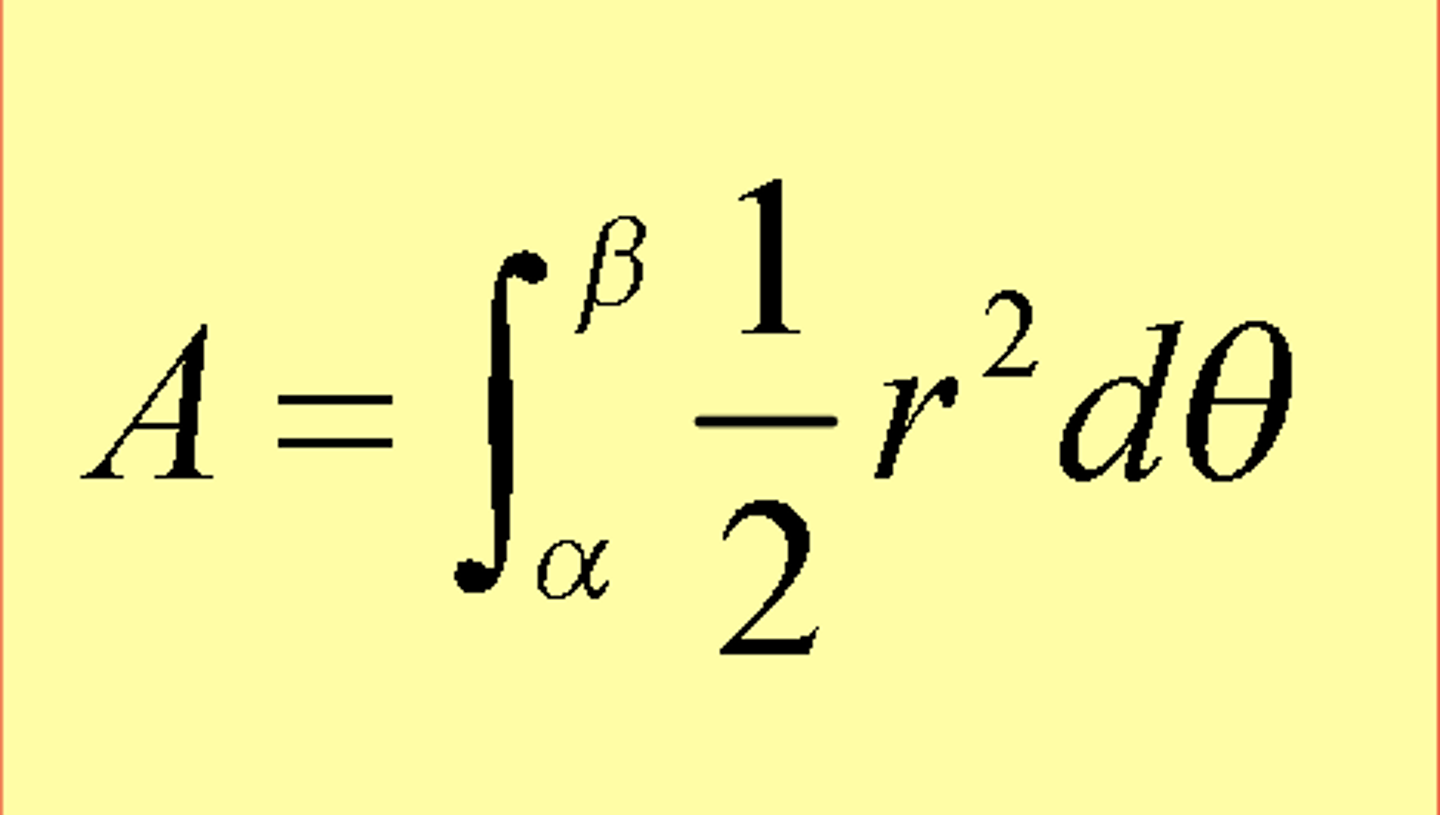
Area between 2 polar curves

1/2 ∫ R² - r² over interval from α to β,

find α and β by setting equations equal, solve for θ.

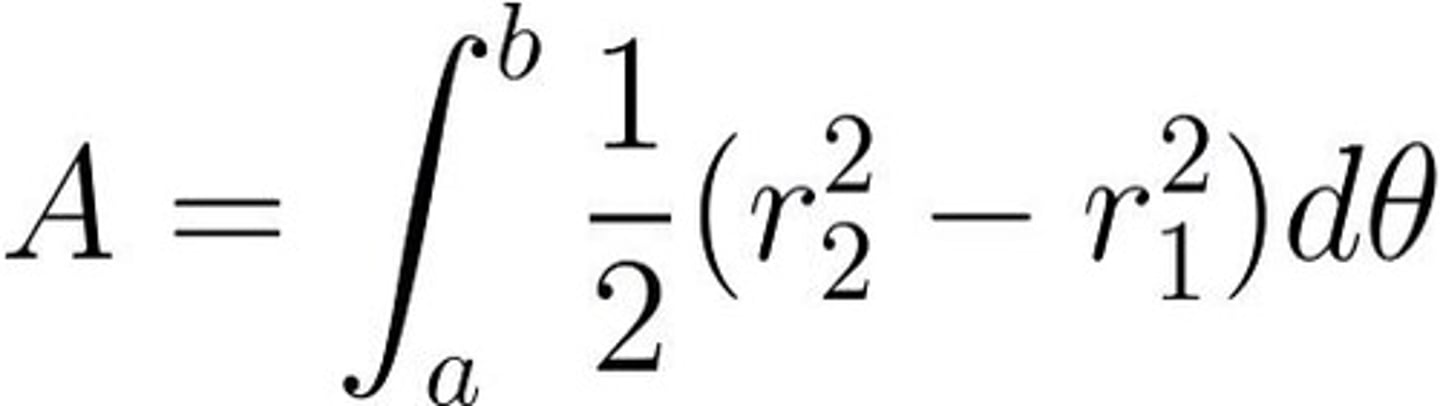
slope of line through origin for polar graphs

θ= tan⁻¹(m)

m=slope

derivative of a vector valued function

take derivative normally, piece by piece

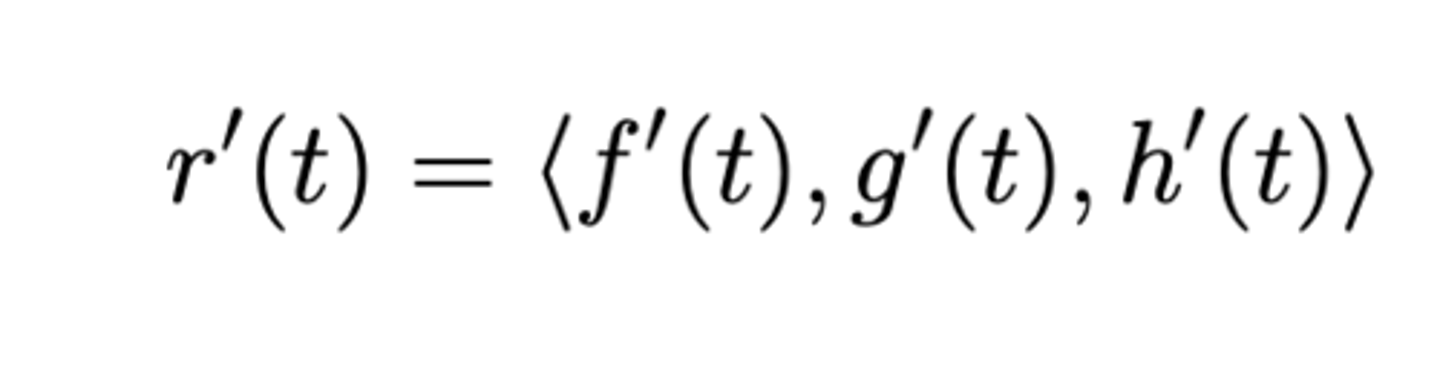
integral of a vector valued function

∫ y(t)x'(t) dt

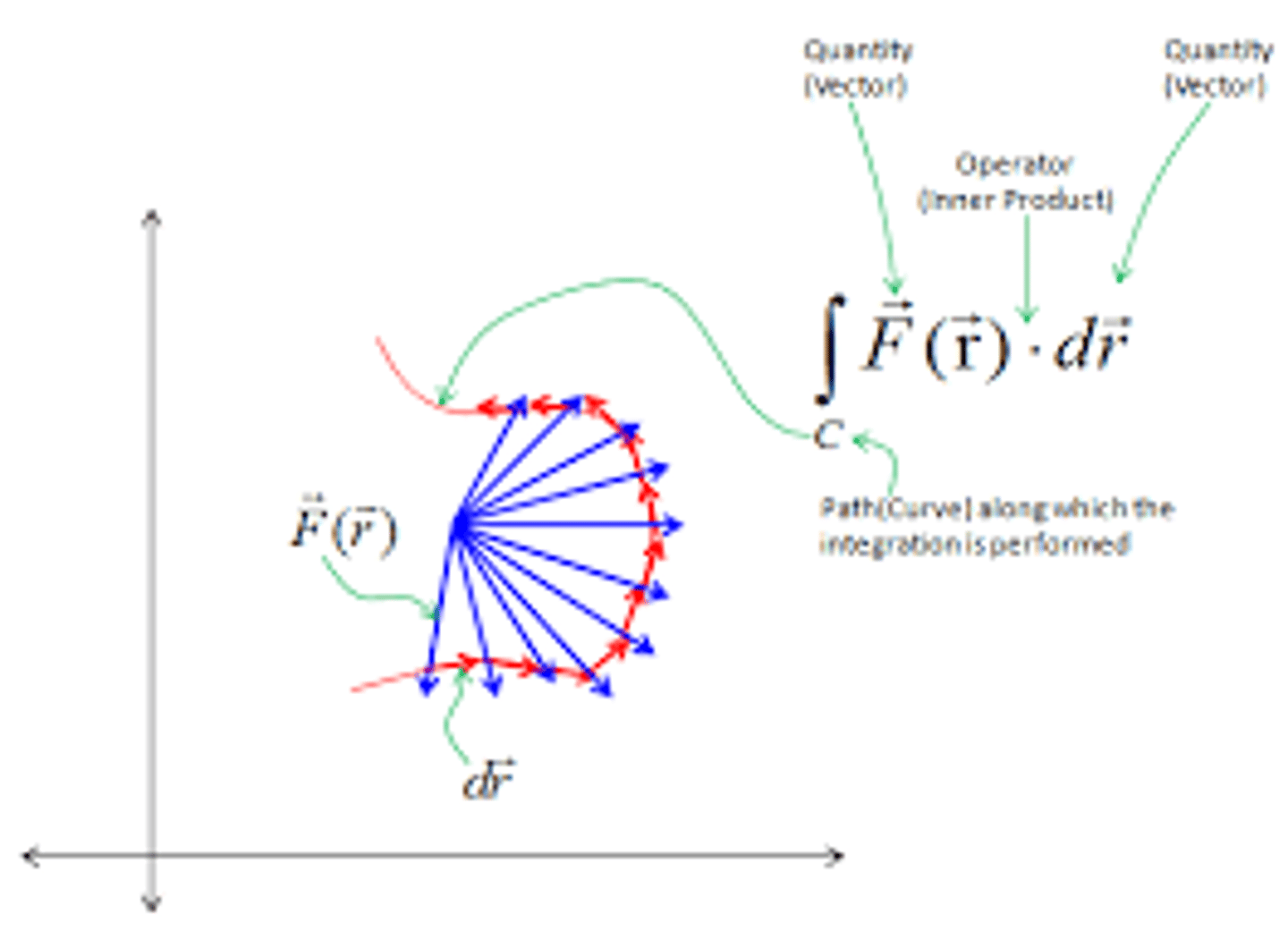
displacement with vector functions

integral of velocity

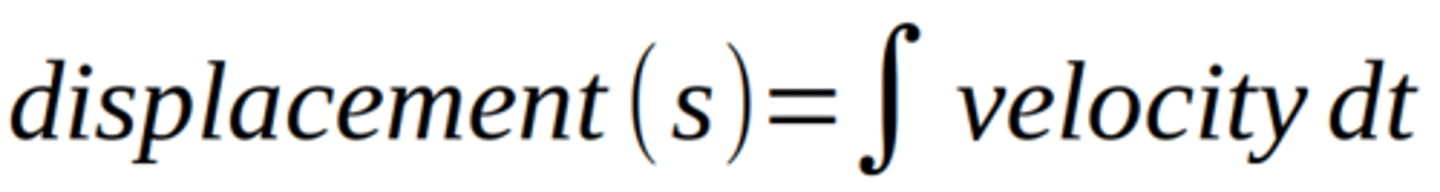
velocity with vector functionss

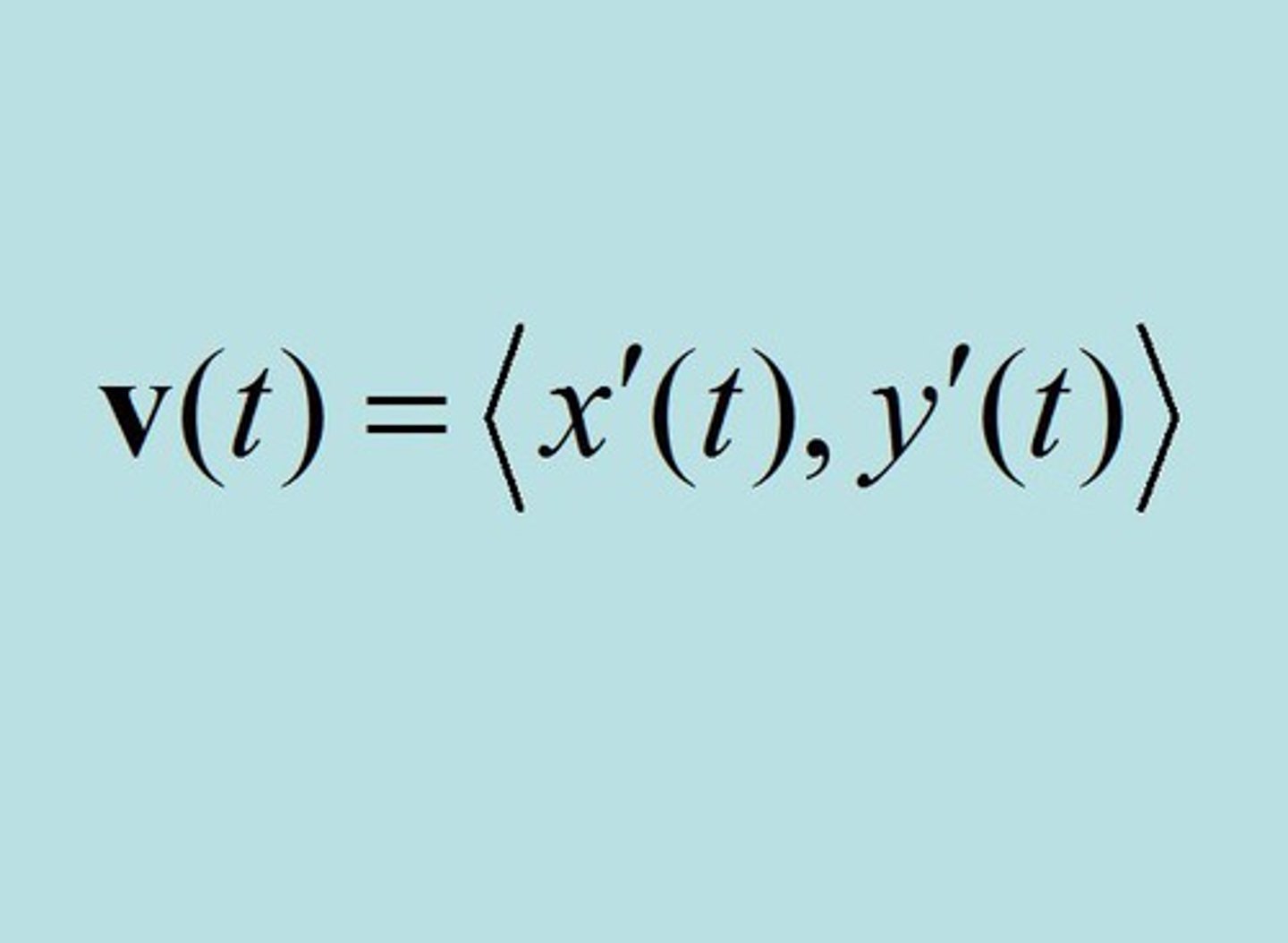
given velocity vectors dx/dt and dy/dt, find speed

(speed with vector functions)

speed= |v(t)|
=
√(dx/dt)² + (dy/dt)² not an integral!

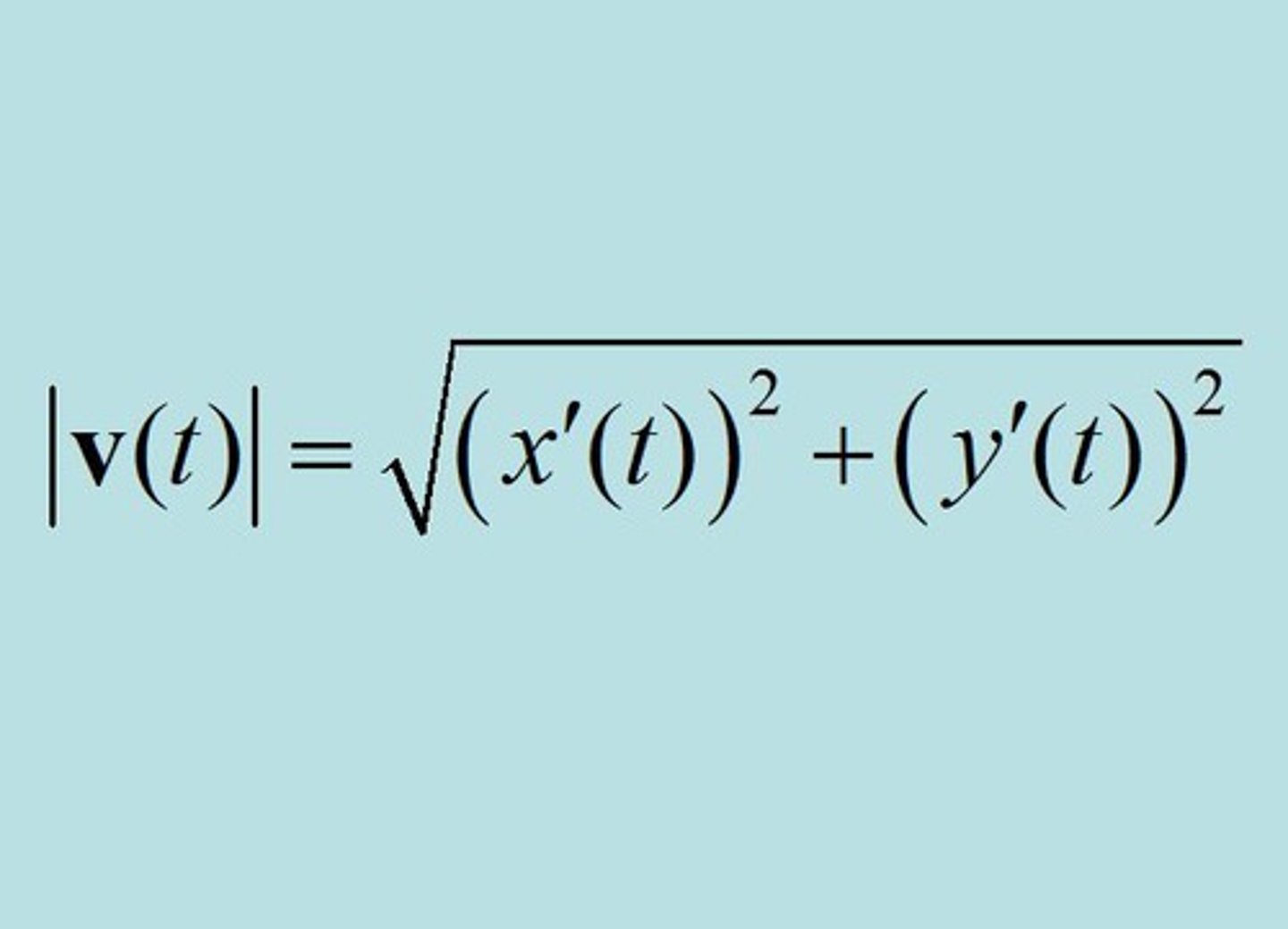
given velocity vectors dx/dt and dy/dt, find total distance travelled

(total distance with vector functions)

total distance= ∫|v(t)|
=
∫ √ (dx/dt)² + (dy/dt)² over interval from a to b

(integral of speed=total distance. integral of previous equation)