Forced Oscillation

Forced Oscillation

When a system is made to oscillate by an external periodic force, rather than oscillating freely at its natural frequency.

Driving Force

A periodic external force that continuously supplies energy to a system to maintain oscillations.
Example: The motion of a motor or a parent pushing a child on a swing.

The system oscillates with the same frequency as the driving force, not its natural frequency. Energy is continually supplied to maintain the motion against damping.

What happens when a system is driven by an external periodic force?

Natural Frequency

The frequency at which a system oscillates when there are no external driving forces or damping.

ω_0 = (k/m)^1/2

Mathematical representation of the Natural Frequency

Resonance

The phenomenon in which the amplitude of oscillation increases dramatically when the driving frequency equals the natural frequency of the system.

Resonance occurs when the driving frequency equals the natural frequency of a system, causing a large increase in amplitude because energy is transferred efficiently to the oscillator. When ω = ω_0

When does the resonance occur?

Because the driving force adds energy in phase with the oscillator’s motion, reinforcing each swing instead of opposing it; Like perfectly timed pushes on a swing.

Why does resonance cause large amplitudes?

Example of Resonance

Piano strings vibrating in response to a singer’s voice, or a child’s swing being pushed at just the right frequency.

The amplitude becomes small, since energy transfer between the driving force and the oscillator is inefficient at non-resonant frequencies

What happens to the amplitude when the driving frequency is much lower or higher than the natural frequency?

Damping reduces the maximum amplitude and broadens the resonance curve, making the system less sensitive to small frequency changes.

How does damping affect resonance?

(F_0)sin(ωt)

Equation of only the external driving force.

m(((d^2)(x))/(dt^2)) + kx + b(dx/dt) = (F_0)sin(ωt)

Equation of Motion for a Driven Damped Oscillator

Steady-State Solution

After initial transients fade, the system oscillates periodically with the same frequency as the driving force

x(t) = Acos(ωt + Φ)

the steady state solution to this differential equation after some time.

Small damping produces a sharp, narrow peak in the amplitude–frequency graph, meaning the system resonates strongly at one specific frequency

What type of damping produces the sharpest resonance?

Because small periodic forces can build up very large amplitudes, potentially causing structural failure, as seen in bridges, turbines, or buildings under rhythmic forces.

Why is resonance in lightly damped systems sometimes dangerous?

A = (F_0)/(((m^2)((ω^2) - ((ω_0)^2))^2 + ((b^2)(ω^2)))^1/2)

Amplitude of Forced Oscillation

When ω is approximately equal to ω_0

When does the amplitude peaks?

A_max = (F_0)/(b(ω_0))

Formula for the maximum amplitude at Resonance occurs when the driving frequency equals the natural frequency and damping is small.

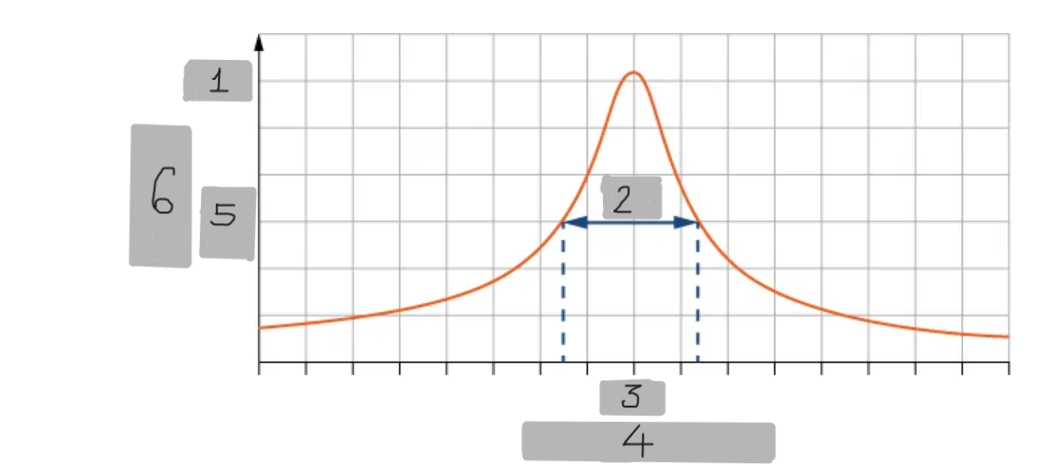
Δω

Symbol that represents the width of the resonance curve at half-maximum amplitude.

Quality Factor

A measure of how sharp or selective the resonance is.

Q = (ω_0)/(Δω)

Mathematical representation of the Quality Factor

High-Q Systems

Systems with small damping that respond strongly only to frequencies very close to the natural frequency.
Example: Radio tuning circuits.

A high Q-factor means the resonance curve is narrow, allowing the radio to select one precise frequency (station) and reject nearby ones.

Why is high-Q resonance desirable in radios?

Low-Q Systems

Systems with large damping that respond to a wide range of frequencies but less strongly.

Transient Motion

The temporary, non-periodic motion that occurs right after an oscillator is disturbed; it fades before steady-state motion begins.

Q = (m(ω_0))/b

Equation of the Quality Factor’s Approximation for the Small Damping

sharper, lower

Higher Q means ______ resonance and _____ energy loss.

lowers, higher and sharper

Larger damping (larger b) ______ the Q, while smaller damping gives a ________________ Q.

That the system has heavy damping and responds weakly to many frequencies, meaning it resonates broadly but less intensely.

What does a low-Q system indicate?

The width (Δω) shows how many frequencies can produce strong oscillations.
A narrow curve indicates selective resonance (high Q); A wide curve indicates broad response (low Q).

What is the significance of the width of the resonance curve?

Damping removes energy from the system each cycle. Less damping allows more stored energy, resulting in a higher peak amplitude.

Why does the amplitude of resonance depend on damping?

Even small rhythmic forces, like synchronized footsteps, can cause dangerous oscillations when they match the bridge’s natural frequency.

What lesson did engineers learn from the Millennium Bridge resonance?

The parent applies small periodic pushes at the swing’s natural frequency, causing the amplitude of the swing’s motion to increase steadily.

Why does a parent pushing a child on a swing represent resonance?

Without damping, there’s no energy loss, so each cycle adds more energy, making amplitude theoretically infinite (though impossible in practice).

Why does a system’s amplitude go to infinity if damping is zero and resonance occurs?

At resonance, the driving force and motion are in phase, so all the work done by the driver goes into increasing the system’s energy, not opposing it.

How does resonance improve energy transfer?

It measures how efficiently the system stores and transfers energy relative to how quickly it loses it, a high-Q system loses little energy per cycle.

What does the quality of a resonant system mean?

Resonance amplifies specific frequencies, allowing instruments like pianos, violins, and flutes to produce strong, clear tones at their natural frequencies.

Why do musical instruments rely on resonance?

A

(1)

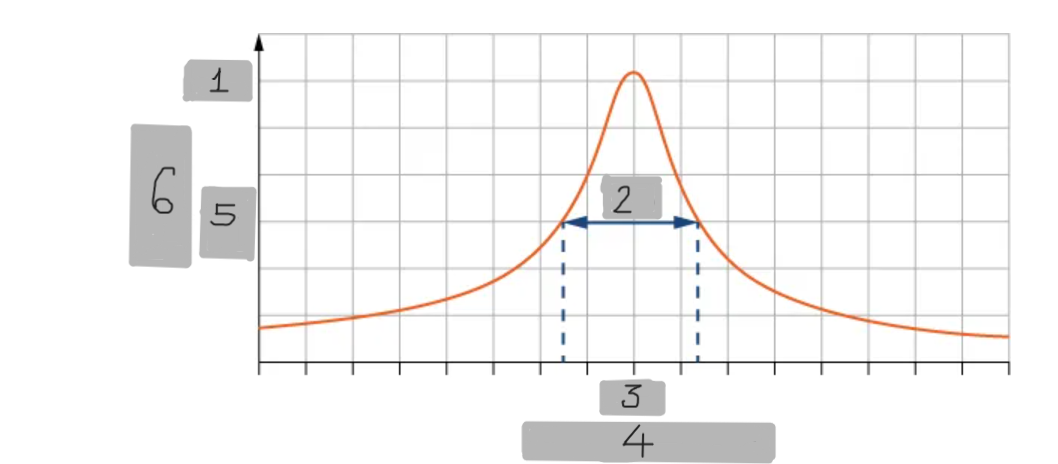
Δω

(2)

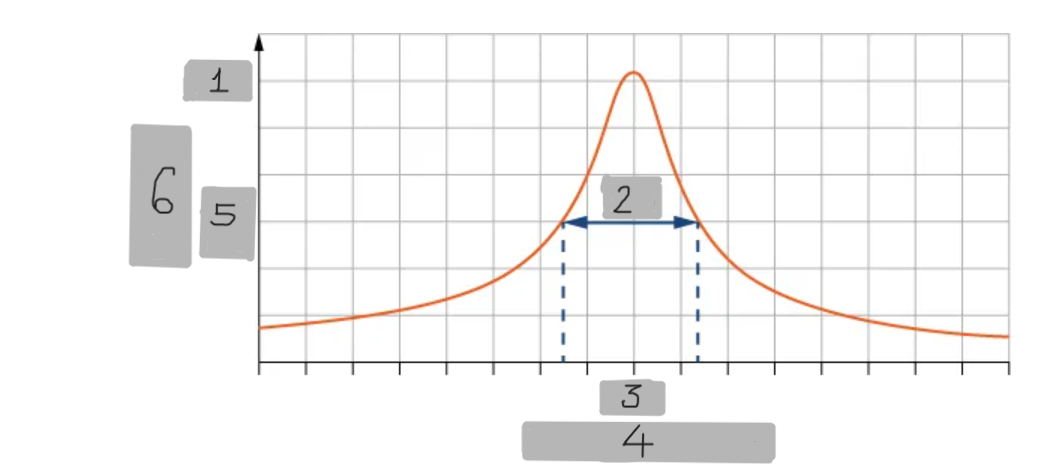
ω_0

(3)

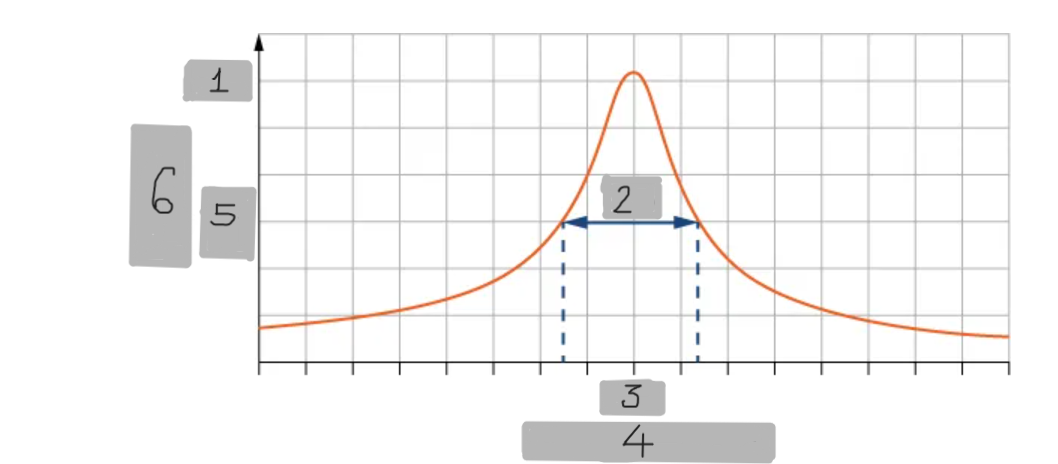
Angular Frequency

(4)

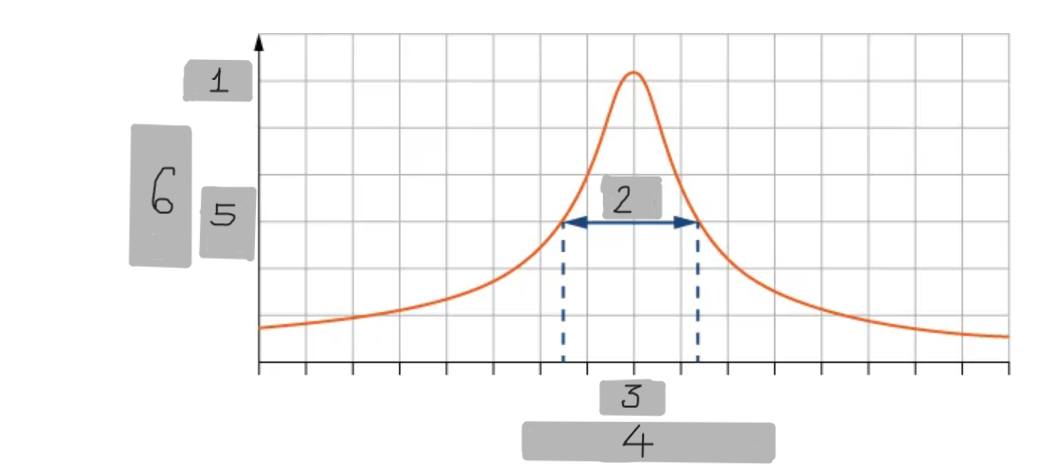
(1/2)A

(5)

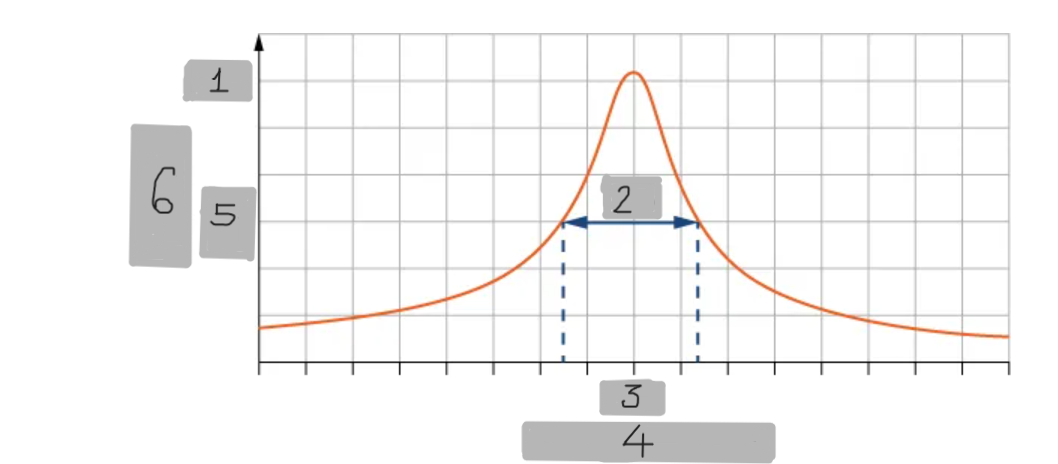
Amplitude

(6)

Small damping

(i)

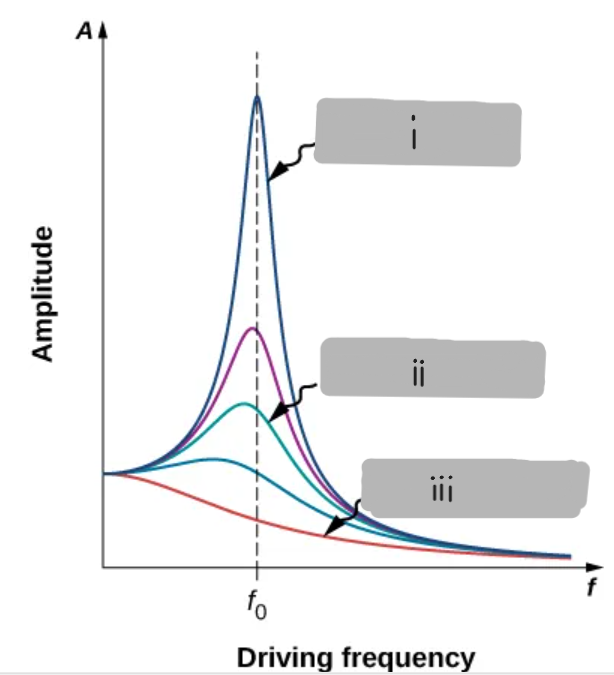
Medium damping

(ii)

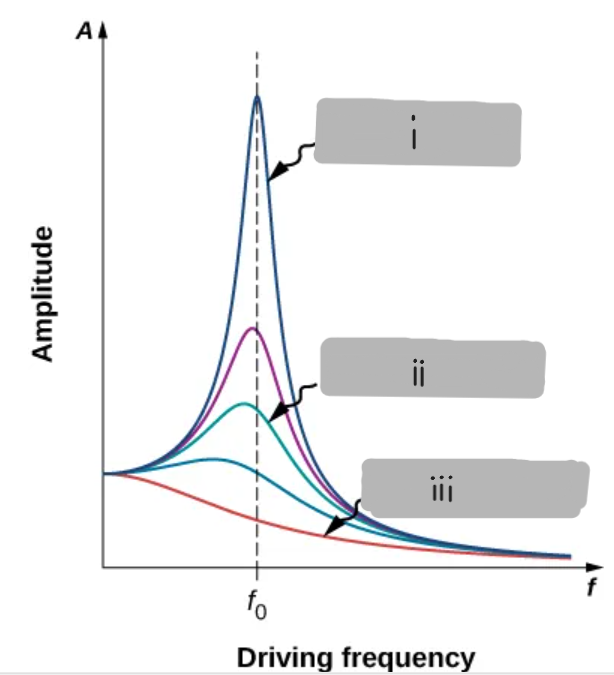
Large damping

(iii)