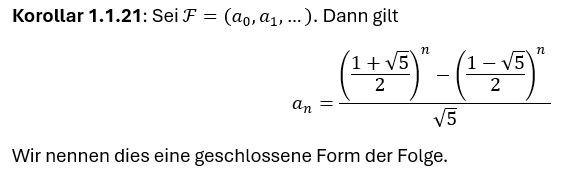Fibonacci Folge

Vocabulary flashcards covering definitions from the Linear Algebra 1 lecture notes.

Fibonacci-Folge (𝑎_𝑛)_𝑛≥0

Definiert durch die Rekursion

𝑎₀ = 0, 𝑎₁ = 1, 𝑎_𝑛 = 𝑎_𝑛−1 + 𝑎_𝑛−2 für 𝑛 ≥ 2

ℱ_𝑎,𝑏

Eine Folge definiert durch die Rekursion

𝑎₀ = 0, 𝑎₁ = 1, 𝑎_𝑛 = 𝑎_𝑛−1 + 𝑎_𝑛−2 für 𝑛 ≥ 2 wobei 𝑎, 𝑏 ∈ ℝ.

V

Die Menge aller Fibonacci-Folgen, d.h. 𝑉 = {ℱ_𝑎,𝑏 ∶ 𝑎, 𝑏 ∈ ℝ}

Summe von ℱ und 𝒢

Definiert als die Folge ℱ + 𝒢 = (𝑎_𝑛 + 𝑏_{𝑛)𝑛≥0,}

wobei ℱ = (𝑎_𝑛)_𝑛≥0 und 𝒢 = (𝑏_𝑛)_𝑛≥0 ∈ 𝑉.

Skalarprodukt von ℱ und 𝛼

Definiert als die Folge 𝛼 ∙ ℱ = (𝛼 ∙ 𝑎_𝑛)_𝑛≥0,

wobei ℱ = (𝑎_𝑛)_𝑛≥0 ∈ 𝑉 und 𝛼 ∈ ℝ.

Struktur eines Vektorraums über ℝ

V hat die Struktur eines Vektorraums über ℝ, wenn für

• ℱ, 𝒢 ∈ 𝑉 gilt ℱ + 𝒢 ∈ 𝑉

• ℱ ∈ 𝑉 und 𝛼 ∈ ℝ gilt 𝛼 ∙ ℱ ∈ 𝑉.

Es gilt…

• ℱ_a,b + ℱ_c,d = ℱ_{a+c, b+d}

• 𝛼 ∙ ℱ_a,b = ℱ_𝛼a,𝛼b

Das Ergebnis ist ebenfalls eine Fibonacci-Folge

Linearkombination

Die Gleichung schreibt ℱ als eine Linearkombination der Folgen ℱ_1,0 und ℱ_0,1, so dass

ℱ = 𝛼 ∙ ℱ_1,0 + 𝛽 ∙ ℱ_0,1

Symmetrie von V

Eine Abbildung 𝑇: 𝑉 → 𝑉 ist eine Symmetrie von V, wenn für alle ℱ, 𝒢 ∈ 𝑉 und 𝛼 ∈ ℝ gilt, dass

𝑇(ℱ + 𝒢) = 𝑇(ℱ) + 𝑇(𝒢) und 𝑇(𝛼 ∙ ℱ) = 𝛼 ∙ 𝑇(ℱ).

T ist eine lineare Abbildung.

Verschiebungs-Abbildung 𝑆 ∶ 𝑉 → 𝑉

Definiert als (𝑎₀, 𝑎₁, … ) ↦ (𝑎₁, 𝑎₂, … )

Eigenfolge

Sei 𝑇 ∶ 𝑉 → 𝑉 eine Symmetrie. Eine Folge ℱ ∈ 𝑉, ℱ ≠ ℱ_0,0 ist eine Eigenfolge, wenn es ein Element 𝛼 ∈ ℝ gibt so dass

𝑇(ℱ) = 𝛼 ∙ ℱ

In diesem Fall heisst 𝛼 der Eigenwert der Folge ℱ.

In der linearen Algebra bezeichnet eine Eigenfolge eine Folge von Vektoren, die bei der Anwendung einer linearen Abbildung oder Matrix auf sich selbst einen bestimmten Faktor (den Eigenwert) erhält, ohne ihre Richtung zu ändern

Eigenfolge der Abbildung S

Geschlossene Form der Folgen