COP4415 - Final Exam
0.0(0)
Card Sorting
1/122
Earn XP
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
123 Terms
1
New cards
binary search trees
* abstract data type
* used for indexing data points
* data structure made of nodes and pointers
* used for indexing data points
* data structure made of nodes and pointers
2
New cards
height
length of the longest path from the root to a leaf in a tree is known as the ______
3
New cards
0
a tree with only 1 node has the height of __
4
New cards
binary tree
each node can have at most 2 children
5
New cards
full binary tree
each node (other than leaves) has exactly 2 children
6
New cards
complete binary tree
every level (except maybe last) is completely filled and all nodes are as far left as possible
7
New cards
full, not complete
full or complete?
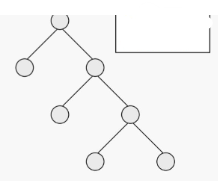
8
New cards
complete, not full
full or complete?
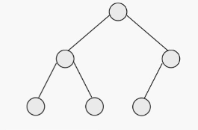
9
New cards
neither
full or complete?
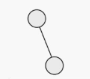
10
New cards
both
full or complete?
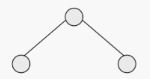
11
New cards
depth first search
explores a path all the way to a leaf before backtracking and exploring another path
12
New cards
breadth first search
* explores levels in order
* every node in a level should be visited before going to next level
* starts at root, ends at leaves
* every node in a level should be visited before going to next level
* starts at root, ends at leaves
13
New cards
binary tree traversals
1\.) preorder
2\.) inorder
3\.) postorder
2\.) inorder
3\.) postorder
14
New cards
preorder traversal
root is visited before its left and right subtrees
15
New cards
inorder traversal
root is visited between the subtrees
16
New cards
preorder traversal
What type of traversal is this?
void traverse(Node\* p) {
if(p != NULL) {
cout << p→data << endl;
traverse(p→left_child);
traverse(p→right_child);
}
}
void traverse(Node\* p) {
if(p != NULL) {
cout << p→data << endl;
traverse(p→left_child);
traverse(p→right_child);
}
}
17
New cards
inorder traversal
What type of traversal is this?
void traverse(Node\* p) {
if(p != NULL) {
traverse(p→left_child);
cout << p→data << endl;
traverse(p→right_child);
}
}
void traverse(Node\* p) {
if(p != NULL) {
traverse(p→left_child);
cout << p→data << endl;
traverse(p→right_child);
}
}
18
New cards
postorder traversal
What type of traversal is this?
void traverse(Node\* p) {
if(p != NULL) {
traverse(p→left_child);
traverse(p→right_child);
cout << p→data << endl;
}
}
void traverse(Node\* p) {
if(p != NULL) {
traverse(p→left_child);
traverse(p→right_child);
cout << p→data << endl;
}
}
19
New cards
4, 8, 1, 3, 9, 2, 5, 0, 6
What is the preorder traversal for this tree?
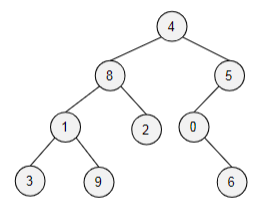
20
New cards
3, 1, 9, 8, 2, 4, 0, 6, 5
What is the inorder traversal for this tree?
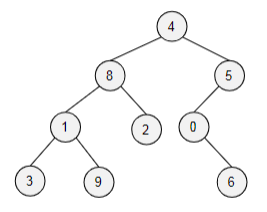
21
New cards
3, 9, 1, 2, 8, 6, 0, 5, 4
What is the postorder traversal for this tree?
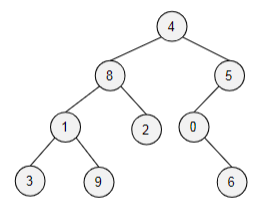
22
New cards
O(logn)
BST time complexity (for insert, search, delete) for a balanced tree
23
New cards
O(n)
BST time complexity (for insert, search, delete) for an unbalanced tree
24
New cards
balanced binary tree
height of left subtree and right subtree of any node differ by at most 1
25
New cards
self-balancing binary tree
height-balanced BSTs that automatically keeps height as small as possible when insertion/deletion is performed on tree
26
New cards
O(logn)
self-balancing BST time complexity
27
New cards
height
* total number of nodes in the longest path from the root to a leaf
* if no node, height is 0
* if 1 node, height is 1
* if no node, height is 0
* if 1 node, height is 1
28
New cards
height
* length of the longest path from the root to a leaf
* if no node, height is -1
* if 1 node, height is 0
* if no node, height is -1
* if 1 node, height is 0
29
New cards
AVL
* a self-balancing BST
* difference between the height of the left and right subtree cannot be more than 1 for all node (balanced)
* difference between the height of the left and right subtree cannot be more than 1 for all node (balanced)
30
New cards
O(logn)
AVL time complexity (for delete, search, insert)
31
New cards
AVL formal definition
1\.) All empty trees are also AVL trees
2\.) If T is a non-empty BST with TL and TR as its left and right subtrees, then T is an AVL tree iff:
* TL and TR are also AVL trees
* |hL - hR|
2\.) If T is a non-empty BST with TL and TR as its left and right subtrees, then T is an AVL tree iff:
* TL and TR are also AVL trees
* |hL - hR|
32
New cards
balance factor
* height of the left subtree minus the height of the right subtree
* hL - hR or hR - hL
* hL - hR or hR - hL
33
New cards
left rotation
What do we do for this case:
1\.) Inserting a new node into the right subtree of a right child (RR)
1\.) Inserting a new node into the right subtree of a right child (RR)
34
New cards
right rotation
What do we do for this case:
2\.) Inserting a new node into the left subtree of a left child (LL) (symmetric case)
2\.) Inserting a new node into the left subtree of a left child (LL) (symmetric case)
35
New cards
right rotation, then left rotation
What do we do for this case:
3\.) Inserting a new node into the left subtree of a right child (RL)
3\.) Inserting a new node into the left subtree of a right child (RL)
36
New cards
left rotation, then right rotation
What do we do for this case:
4\.) Inserting a new node into the right subtree of a left child (LR) (symmetric case)
4\.) Inserting a new node into the right subtree of a left child (LR) (symmetric case)
37
New cards
right rotation
This is what type of rotation?
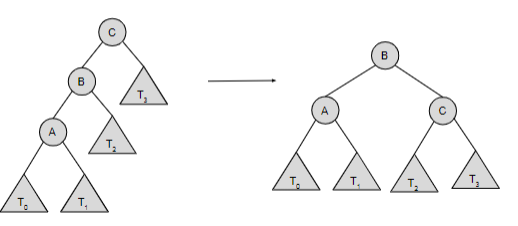
38
New cards
left rotation
This is what type of rotation?
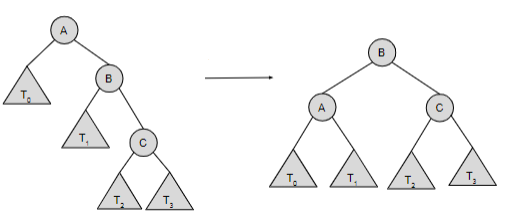
39
New cards
heap
* an abstract data type
* must be a complete binary tree
* must be a complete binary tree
40
New cards
max heap
* all values stored in the subtree of a given node are less than or equal to the value stored in the node
* root stores highest value of any given subtree
* root stores highest value of any given subtree
41
New cards
min heap
* all values stored in the subtree of a given node are greater than or equal to the value stored in that node
* root stores the smallest value of any given subtree
* root stores the smallest value of any given subtree
42
New cards
binary heaps
used to implement another abstract data type → priority queues
43
New cards
priority queue
* elements are inserted in order of arrival
* element with highest priority is processed/removed first
* element with highest priority is processed/removed first
44
New cards
O(logn)
time complexity of percolate up/down
45
New cards
True
(T/F) In a priority queue, we always delete the element with the highest priority (the root)
46
New cards
O(logn)
time complexity of deleting nodes from binary heap
47
New cards
O(nlogn)
time complexity of building a heap from scratch
48
New cards
O(n)
heapify time complexity
49
New cards
O(nlogn)
heap sort time complexity
50
New cards
graph
* collection of nodes (vertices) and the connections between them (edges)
51
New cards
simple graph
G = (V, E) consists of a finite set denoted by V and a collection E of unordered pairs {u, v} of distinct elements from V
52
New cards
vertex
* each element of V
* AKA point, node
* AKA point, node
53
New cards
edge
* each element of E
* AKA link
* AKA link
54
New cards
order of graph
* number of vertices (cardinality of V)
* denoted by |V|
* denoted by |V|
55
New cards
size of graph
* cardinality of E
* denoted by |E|
* denoted by |E|
56
New cards
path
sequence of edges denoted by v1, v2, …., v_n-1, v_n
57
New cards
cycle
If v1 = v_n, then the path is a _______.
58
New cards
adjacent
2 vertices are _____ or neighbors if there’s an edge between them
59
New cards
degree
number of edges incident with a vertex v is the _____ of the vertex
60
New cards
graph representations
1\.) adjacency list
2\.) adjacency matrix
2\.) adjacency matrix
61
New cards
adjacency list
* each vertex adjacent to a given vertex is listed
* space: O(|V| + |E|)
* takes O(|V|) time to check if vertex u is adjacent to vertex v
* space: O(|V| + |E|)
* takes O(|V|) time to check if vertex u is adjacent to vertex v
62
New cards
adjacency matrix
* |V| x |V| binary matrix
* A(u,v) = 1 if (u,v) is an edge, else it equals 0
* space: O( |V|^2 )
* O(1) time to check if vertex u is adjacent to vertex v
* (|V|) time to list all neighbors
* A(u,v) = 1 if (u,v) is an edge, else it equals 0
* space: O( |V|^2 )
* O(1) time to check if vertex u is adjacent to vertex v
* (|V|) time to list all neighbors
63
New cards
BFS theorem
A vertex v is discovered in Round k iff the shortest distance of v from source S is k
64
New cards
O(|V| + |E|)
total time for BFS algorithm
65
New cards
O(|V| + |E|)
total space for BFS algorithm
66
New cards
BFS algorithm
* implemented using common queue:
* when vertex is discovered, put it at end of queue
* next vertex to visit is the one at front of queue
* finished when no more vertices in queue
* when vertex is discovered, put it at end of queue
* next vertex to visit is the one at front of queue
* finished when no more vertices in queue
67
New cards
DFS algorithm
An alternative algorithm to find all vertices reachable from a particular source vertex S
68
New cards
O(|V| + |E|)
total time for DFS
69
New cards
tree
connected graph with no cycles
70
New cards
n-1
a tree with n vertices has ____ edges
71
New cards
spanning tree
* a tree that spans undirected and connected graph G and is a subgraph of G
* includes every vertex of G and every edge in the tree belongs to G
* includes every vertex of G and every edge in the tree belongs to G
72
New cards
cost of spanning tree
sum of the weights of all edges in the tree
73
New cards
minimum spanning tree
spanning tree where the cost is minimum among all the spanning trees
74
New cards
spanning forest
if graph isn’t connected, there is a spanning tree for each connected component of the graph
75
New cards
greedy algorithm
* simple, intuitive algorithm used in optimization problems
* tries to find overall optimal way to solve entire problem
* tries to find overall optimal way to solve entire problem
76
New cards
kruskal’s algorithm
* builds spanning tree by adding edges one by one into growing spanning tree
* follows greedy approach → finds an edge with least weight and adds it to tree
* follows greedy approach → finds an edge with least weight and adds it to tree
77
New cards
O(|V| log|V|)
kruskal’s algorithm time complexity
78
New cards
prim’s algorithm
* keeps track of vertices already included in MST
* picks vertices with minimum key value to add to MST and updates key value of all adjacent vertices
* picks vertices with minimum key value to add to MST and updates key value of all adjacent vertices
79
New cards
O(E logV)
prim’s algorithm time complexity
80
New cards
selection sort
* Given an array of n numbers, sort the array in n steps
* Steps
* Scan the entire array and find smallest element
* Swap smallest element with element at index i
* Increment i
* Repeat until i = n
* Steps
* Scan the entire array and find smallest element
* Swap smallest element with element at index i
* Increment i
* Repeat until i = n
81
New cards
O(n^2)
selection sort time complexity
82
New cards
merge sort
* Using divide and conquer, break down the array and sort each part
* Then, merge the pieces back together
* Then, merge the pieces back together
83
New cards
O(nlogn)
merge sort time complexity
84
New cards
table
abstract data type that stores and retrieves
85
New cards
record
each individual row in the table
86
New cards
hash table
implemented using an array to store records in unsorted order
87
New cards
unsorted array
runtime complexity:
* adding a record: O(1)
* deleting a record: O(n)
* searching for a record: O(n)
* adding a record: O(1)
* deleting a record: O(n)
* searching for a record: O(n)
88
New cards
sorted array
runtime complexity:
* adding a record: O(n)
* deleting a record: O(n)
* searching for a record: O(logn) → binary search
* adding a record: O(n)
* deleting a record: O(n)
* searching for a record: O(logn) → binary search
89
New cards
binary tree
runtime complexity:
* adding a record: O(logn)
* deleting a record: O(logn)
* searching for a record: O(logn)
* adding a record: O(logn)
* deleting a record: O(logn)
* searching for a record: O(logn)
90
New cards
direct access table
runtime complexity:
* adding a record: O(1)
* deleting a record: O(1)
* searching for a record: O(1)
* adding a record: O(1)
* deleting a record: O(1)
* searching for a record: O(1)
91
New cards
direct access table
* special type of array
* each record has own exclusive cell → large array
* pro: O(1) time complexity for everythin
* con: space complexity is huge
* each record has own exclusive cell → large array
* pro: O(1) time complexity for everythin
* con: space complexity is huge
92
New cards
hash table
array of table items, where index is calculated by a hash function
93
New cards
hash function
* a mathematical calculation that maps the search key to an index in a hash table
* time complexity for calculating: O(1)
* time complexity for calculating: O(1)
94
New cards
hashing
* a way to access a table/array in constant time
* uses a hash function and collision resolution scheme
* uses a hash function and collision resolution scheme
95
New cards
collision
* when a hash function maps 2+ search keys into the same location in a hash table
* h(key1) = h(key2)
* h(key1) = h(key2)
96
New cards
hash functions for integers
1\.) Selecting digits
2\.) Folding
3\.) Modulo arithmetic
2\.) Folding
3\.) Modulo arithmetic
97
New cards
selecting digits
* only select a few digits instead of whole integer
* ex: h(4324494421) = 432
* pro: fast and easy to calculate
* con: does not distribute randomly
* ex: h(4324494421) = 432
* pro: fast and easy to calculate
* con: does not distribute randomly
98
New cards
folding
* adds digits of the integer together
* ex: h(123456789) = 1+2+3+4+5+6+7+8+9 = 45
* can add in different ways for hash tables of diff sizes:
* ex: h(123456789) = 123+456+789 = 1368
* ex: h(123456789) = 1+2+3+4+5+6+7+8+9 = 45
* can add in different ways for hash tables of diff sizes:
* ex: h(123456789) = 123+456+789 = 1368
99
New cards
modulo arithmetic
* uses prime number for table size to reduce collisions
* h(x) = x mod (tableSize)
* ex: h(123456789) = 123456789 mod 31 = 2
* h(x) = x mod (tableSize)
* ex: h(123456789) = 123456789 mod 31 = 2
100
New cards
perfect hash function
ideal situation where hash function maps each search key into a diff location in the hash table (no collisions)