Discrete Math Final
0.0(0)
Card Sorting
1/185
Earn XP
Description and Tags
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
186 Terms
1
New cards
Increasing function
if ∀x1∀x2(x1 < x2 → f (x1) ≤ f (x2))
2
New cards
Strictly Increasing Function
∀x1∀x2(x1 < x2 → f (x1) < f (x2))
3
New cards
Increasing vs. Strictly Increasing functions
Increasing functions can have flat points, so previous points could have the same output as future points. But this is not the case for strictly increasing functions.
4
New cards
Decreasing Function
∀x1∀x2 (x1 < x2 → f (x1) ≥ f (x2))
5
New cards
Strictly Decreasing Function
∀x1∀x2 (x1 < x2 → f (x1) > f (x2))
6
New cards
Decreasing vs Strictly Decreasing Functions
Same as Increasing vs Strictly increasing, no flat points allowed
7
New cards
Injective functions
Every image has a unique pre-image. Ex: f(x) = x+1 (R to R), f(x) = x^2 (Z+ to Z+)
8
New cards
Injective Functions are also known as...
one-to-one functions
9
New cards
Surjective functions
For every element of the co-domain, there is a corresponding pre-image in the domain. (codomain = range). Ex: f(x) = x + 1, from Z to Z
10
New cards
Surjective functions are also called..
Onto Functions
11
New cards
Bijective Functions
When a function is both injective and surjective, it is a bijective functions. (Both one-to-one and onto). Ex: f: {a, b, c, d} → {1, 2, 3, 4} with f (a) = 4, f (b) = 2, f (c) = 1, and f (d) = 3
12
New cards
Different Functions Example
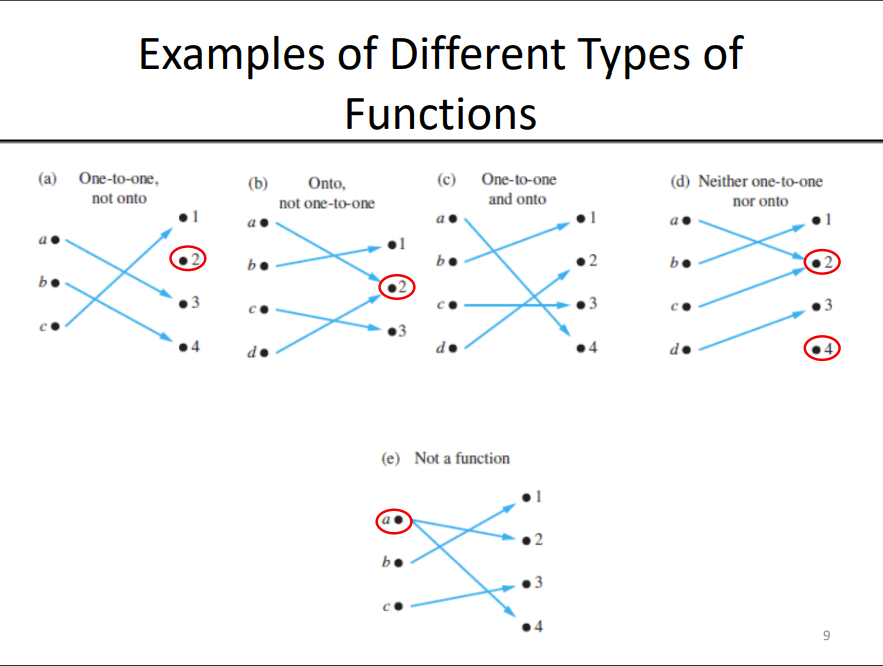
13
New cards
How to show that a function is one-to-one?
Show that if f(x) = f(y) for some x and y of the domain, then x = y.
14
New cards
How to show that function is not one-to-one?
Find x and y such that f(x) = f(y) and x ≠ y
15
New cards
How to show that function is onto?
Take an arbitrary element y from the co-domain, show that there is an element x from the domain such that f(x) = y
16
New cards
How to show that f is not onto?
Find an arbitrary y belonging to the co-domain such that f (x) ≠ y for all x ∈ A.
17
New cards
How to show that a function is bijective?
Show that function is both injective and surjective
18
New cards
Inverse functions
The function that maps B to A (given original function mapped from A to B). In other words, g(y) = x iff f(x) = y
19
New cards
What kind of functions are invertible?
Only bijective functions
20
New cards
Composition
if f maps B to C and g maps A to B, composition function h = f o g(x) = f(g(x)) will map from A to C
21
New cards
Function Graphs
The points such that one coordinate belongs to the domain and other to the range and f(a) = b. (not lines, dots, we're dealing with integers here)
22
New cards
Floor Function
f(x) = ⌊x⌋. The largest integer less than or equal to x.
23
New cards
Ceiling Function
f(x) = ⌈x⌉. The smallest integer greater than or equal to x.
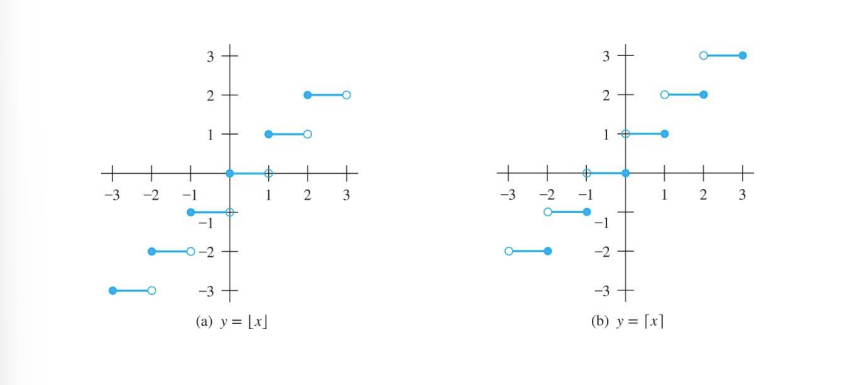
24
New cards
Floor and Ceiling Function Properties
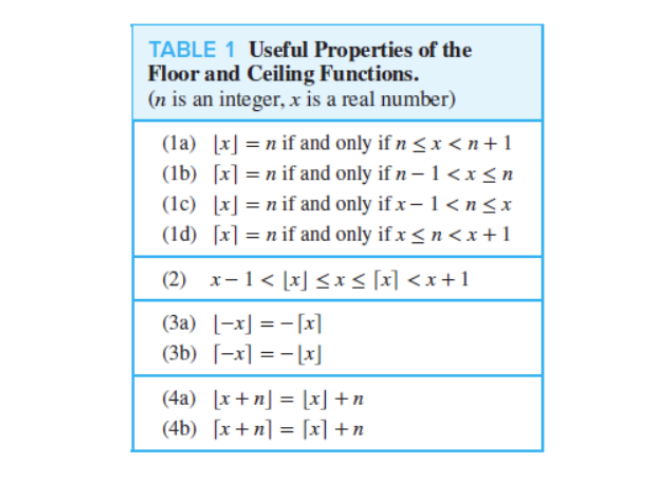
25
New cards
Factorial Functions
f(n) = 1*2*3*....*(n-1)*n. The product of the first n positive integers when n is a nonnegative integer.
26
New cards
Stirling's Formula
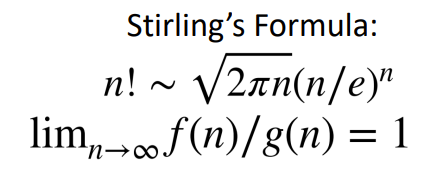
27
New cards
Partial Functions
An assignment of each element of the domain to a unique element in the co-domain. This means there can be holes (in graphs)
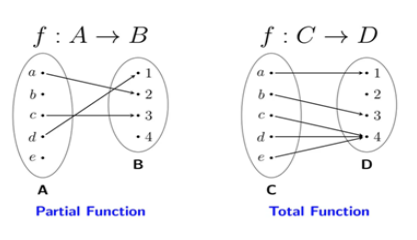
28
New cards
Sequences
Ordered lists of elements. Indices are important with sequences. Used in mathematics, computer science and other disciplines like botany and music.
29
New cards
Sequences (2)
A function from the subset of integers to a set S.
30
New cards
Geometric Progression
A sequence of the form a, ar, ar^2....ar^n. a is the initial term and r is the common ratio
31
New cards
Arithmetic Progression
A sequence of the form a, a+d, a+2d...a+nd. Here a is the initial term and d is the common difference.
32
New cards
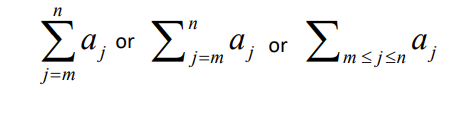
Summations
The sum of the terms am, am+1, ...an. Here j is the index of summation. m is the lower limit and n is the upper limit.
33
New cards
Geometric Series
Sums of terms of geometric progression
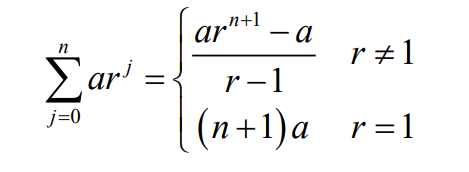
34
New cards
Useful summation formulae
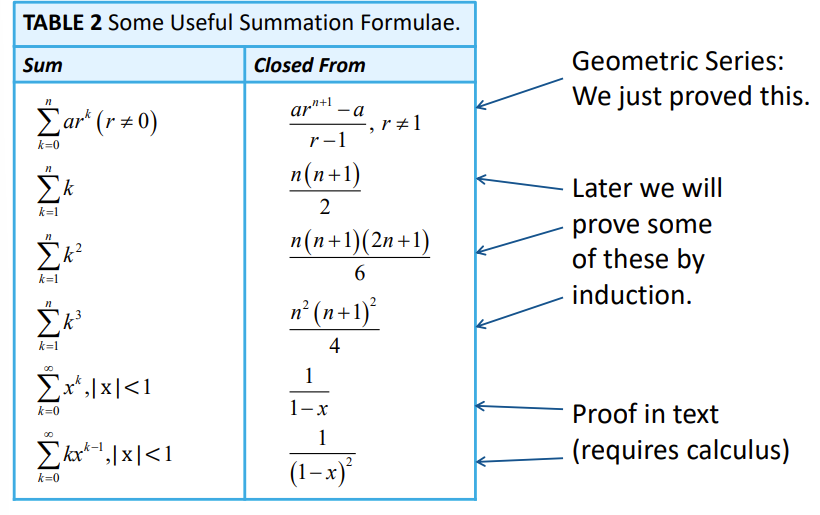
35
New cards
The first step in solving computational problems..
precisely state the problem, using
the appropriate structures to specify the input
and the desired output
the appropriate structures to specify the input
and the desired output
36
New cards
Algorithm
An algorithm is a finite set of precise instructions for performing a computation or for solving a problem
37
New cards
Algorithms can be specified in different ways
Human Language, Flowchart, Pseudocode
38
New cards
Pseudocode
an intermediate step between an English language description of the steps and coding of these steps using a programming language
39
New cards
Flowchart
Graphical representation of an algorithm. Different types of instructions are represented by boxes of different shapes. The flow of control is represented by directional lines. Con is it gets complicated pretty quickly.
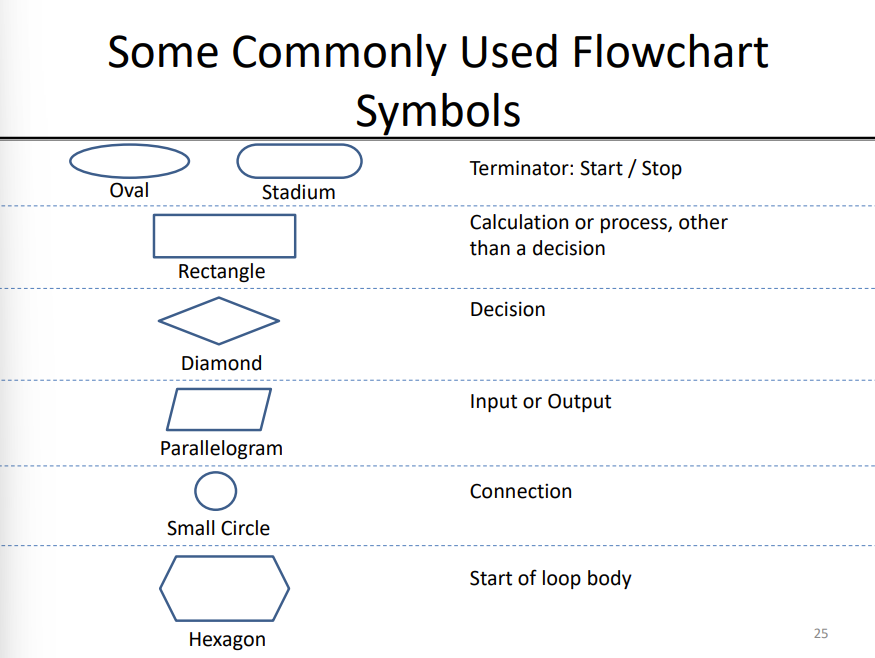
40
New cards
Properties of Algorithms
Input: An algorithm typically has input values from a specified set.
Output: The algorithm performs an action or produces the output values from a specified set (the solution).
Correctness: An algorithm should produce the correct output values for each set of input values.
Finiteness: An algorithm should produce the output after a finite number of steps for any input.
Effectiveness: It must be possible to perform each step of the algorithm correctly and in a finite amount of time.
Generality: The algorithm should work for all problems of the desired form.
Output: The algorithm performs an action or produces the output values from a specified set (the solution).
Correctness: An algorithm should produce the correct output values for each set of input values.
Finiteness: An algorithm should produce the output after a finite number of steps for any input.
Effectiveness: It must be possible to perform each step of the algorithm correctly and in a finite amount of time.
Generality: The algorithm should work for all problems of the desired form.
41
New cards
Algorithm Problem Types
Searching Problems, Sorting problems, Optimizations Problems
42
New cards
Searching Problems
Finding the position of a particular element in a list
43
New cards
Sorting Problems
Putting the elements of a list into increasing order
44
New cards
Optimization Problems
Determining the optimal value of a particular quantity over all possible inputs.
45
New cards
Heuristic Algorithms
An algorithm that quickly produces good, but not necessarily optimal solutions
46
New cards
Linear search algorithm
Locates an item in a list by examining elements in the sequence one at a time, starting at the beginning
47
New cards
Binary Search
Cuts the list in half each time when searching. Sorted list, checks mid value, if smaller searches up else searches down.
48
New cards
Sorting
To sort elements of a list is to put them in increasing order.
49
New cards
Why is sorting an important problem?
Sorting takes a lot of resources. There's a lot algorithms that have been developed for efficient sorting that are studied extensively. Illustrate the basic notions of computer science.
50
New cards
How many sorting algorithms have been developed till date?
More than 100
51
New cards
Examples of common sort algorithms
Binary, Insertion, Bubble, Selection, Merge, Quick and Tournament
52
New cards
Bubble Sort
Multiple passes, swaps when out of order. With each iteration the highest remaining number "sinks" to its correct position.

53
New cards
Selection Sort
Finds the smallest element and brings it to the front of the list.

54
New cards
Insertion sort
Like sorting cards. Goes to element, checks against sorted portion, puts it in the correct spot.

55
New cards
Greedy Algorithms
An optimization algorithm. Makes the best choice at each step. This could mean making a unsustainable solution at the end as a total.
56
New cards
Greedy Change Making Algorithm

57
New cards
Greedy Scheduling Algorithm
Talk that ends the soonest

58
New cards
Halting Problem
A program that tells if a program can stop or will run forever is impossible to create. Alan Turing. Proof by contradiction, feeding the program itself
59
New cards
Growth of Functions
Algorithm efficiency is evaluated and compared by seeing how fast the problem can be solved given a growing size of input
60
New cards
Factors that affect the runtime of a program
1. The size of the input to the program *
2. The time complexity of the algorithm underlying the program *
3. The quality of code generated by the compiler used to create the object program
4. The nature and speed of the instructions on the machine used to execute the program
2. The time complexity of the algorithm underlying the program *
3. The quality of code generated by the compiler used to create the object program
4. The nature and speed of the instructions on the machine used to execute the program
61
New cards
Big O Notation
f(x) is O(g(x)) if f(x) grows slower than g(x). |f(x)|
62
New cards
Parts of Big O
C - constant of multiplication
k - the point where g(x) goes over f(x)
these two combined are called witnesses
k - the point where g(x) goes over f(x)
these two combined are called witnesses
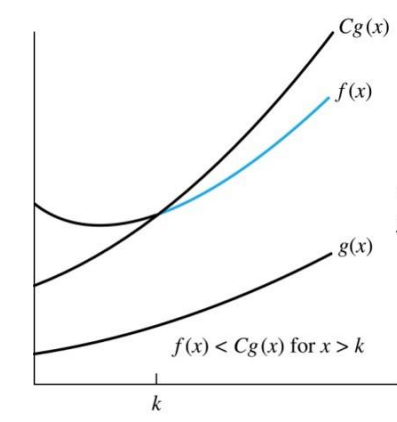
63
New cards
A property of a pair of witnesses
you can pick any C greater, say C' and this C'g(x) would still continue to satisfy the the big O inequality.
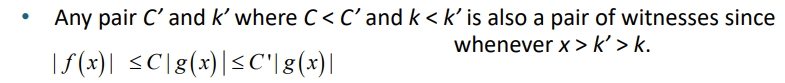
64
New cards
Big O of any polynomial function is...
The highest power
65
New cards
Big O estimates for some functions
1+2+3+...+n -> O(n^2)
n! -> O(n^n)
n! -> O(n^n)
66
New cards
log(n!)
O(nlog(n))
67
New cards
Growth of functions visual
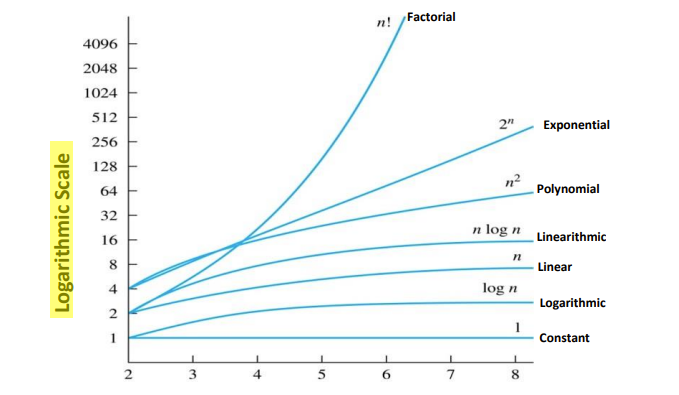
68
New cards
Combinations of functions
f1+f2 -> O(max of the two)
f1*f2 -> O(both big o product)
f1*f2 -> O(both big o product)
69
New cards
Big Omega Notation
gives the lower bound on the growth of a function. It tells us that a function grows at least as fast as another.
70
New cards
Big-Omega Inequality
|f(x)| >= C|g(x)| when x > k
71
New cards
Big Theta Notation
f(x) is big theta of g(x) if big o of g(x) and big omega of g(x)
72
New cards
Big Theta Inequality
C1g(x) < f(x) < C2g(x)
73
New cards
Big Theta polynomial estimate
highest order exponent is big theta
74
New cards
What questions do we ask when checking how efficient an algorithm is?
How much time does this algorithm take? How much memory does this algorithm use?
75
New cards
Time-Complexity
When we analyze the time the algorithm uses to solve the problem given input of a particular size
76
New cards
When we analyze the computer memory the algorithm uses to solve the problem given input of a particular size
77
New cards
Space-Complexity analyzes..
the extra memory needed to solve the problem. So storing the input itself doesn't matter.
78
New cards
Time-complexity analyzes..
the number of operations it takes to arrive at the solution
79
New cards
Focus of time-complexity analysis
lies in the worst-case complexity (big O), the upper bound. It is harder to determine the average-case complexity (big Theta).
80
New cards
Time-Complexity of some algorithms
Linear search: Θ(n)
Binary search: Θ(log n)
Bubble Sort: Θ(n^2)
Selection Sort: Θ(n^2)
Insertion Sort: Θ(n^2)
Matrix Multiplication (n x n): Θ(n^3)
Binary search: Θ(log n)
Bubble Sort: Θ(n^2)
Selection Sort: Θ(n^2)
Insertion Sort: Θ(n^2)
Matrix Multiplication (n x n): Θ(n^3)
81
New cards
Complexity chart
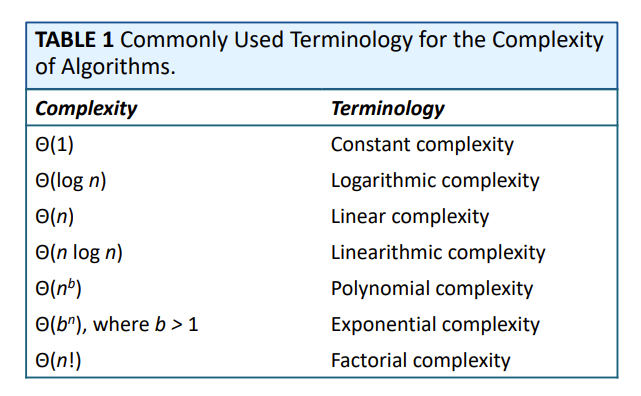
82
New cards
Tractable Problem
There exists a polynomial time algorithm to solve this problem. Belongs to Class P.
83
New cards
Intractable Problem
There does not exist a polynomial time algorithm to solve this problem
84
New cards
Unsolvable Problem
No algorithm exists to solve this problem (halting problem)
85
New cards
Class NP
Solution can be checked in polynomial time. But no polynomial time solution has been found for problems in this class.
86
New cards
NP complete class
if we find a polynomial time time solution for one member of the class, it can be used to solve all the problems in the class
87
New cards
P vs NP
are there problems that can be checked in polynomial time but cannot be solved in polynomial time? not discovering does not mean that it doesn't exist
88
New cards
Number theory
part of mathematics devoted to the study of integers and their properties
89
New cards
Application of number theory
cryptography, pseudorandom number generation, error detection and error correction codes
90
New cards
Division
If a and b are integers with a ≠ 0, then a divides b if there exists an integer c such that b = ac
91
New cards
a|b
this means a "divides" b. another way to think about this b/a is an integer.
92
New cards
a|b is a..
boolean function. true when remainder is equal to 0
93
New cards
Properties of divisibility
if a|b and a|c then a|(b+c)
if a|b then a|bc for all integers c
if a|b and b|c, then a|c
if a|b then a|bc for all integers c
if a|b and b|c, then a|c
94
New cards
Division terms
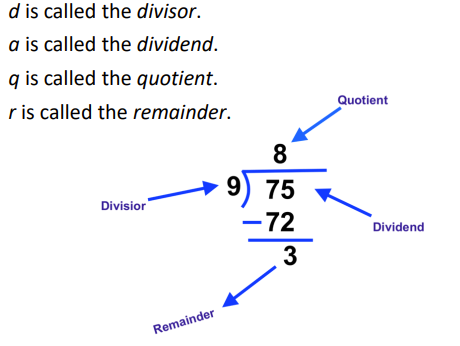
95
New cards
positive and negative remainders
+1 the multiplication, take the difference. normally, 18/5 is q: 3 and remainder 3. but negative remainder would work like q: 4 and 4: -2
96
New cards
Congruence
Two integers a and b are said to be congruent modulo m if a mod m = b mod m
97
New cards
a is congruent to b modulo m
if m divides a-b
98
New cards
a is congruent to b modulo m (2)
if there is an integer such that a = b + km
99
New cards
Congruence Class
The set of all integers congruent to a mod m is called the congruence class of a modulo m
100
New cards
if a is congruent to b mod m, and c is congruent to d mod m then...
a+c is congruent to b+d mod m and ac is congruent to bd mod m