Lecture 2: 1D and 2D Kinematics

Mechanics

study of motion, forces and energy

Kinematics

description of motion (how things move)

Dynamics

causes of motion (why things move)

Translational Motion

objects moving along lines, ignoring internal motion

Displacement

must include directions either with a ± sign or with words (“to the left” etc.)

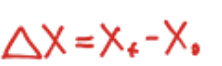
Distance

magnitude of displacement; pure number with units

Distance traveled

total length of the path

Scalars (s)

quantities that only have magnitude (mass, distance, temp)

vectors (v)

quantities with both magnitude and direction (force and displacement)

Reference frame

from what position must be described with respect to (standard coordinates)

Elapsed time

when one event happens at t0 and another at tf; often t0 = 0 and tf = t ( elapsed time = t)

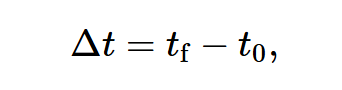
average speed

distance traveled / time taken; scalar quantity because distance is scalar

average velocity

displacement / time traveled; vector because displacement is a vector

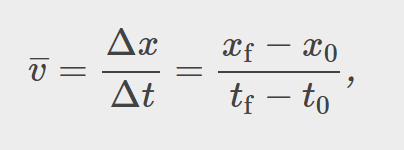
Travel furthest path

moving steadily in a straight lin e

distance traveled

average velocity x time

time

distance traveled/ displacement divided by average velocity

Find average velocity given two different velocities

find total distance then divide by total time

Acceleration

rate of change of velocity; change of velocity/time taken

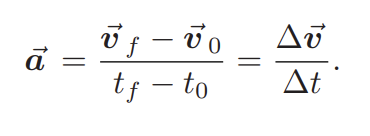
Equation A of motion (Constant Acceleration)

given v and vo and looking for t

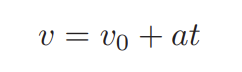
Equation B of motion (Constant Acceleration)

use given x0, v0, and t and need to find x; also use to find t given x,x0, and v0

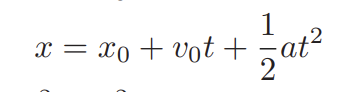
Equation C of motion (Constant Acceleration)

given x, x0, and v0 looking for v

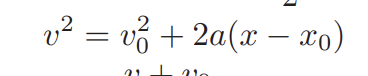
Equation D of motion (Constant Acceleration)

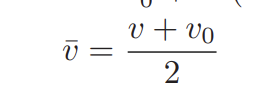
Why is there so many kinematic equations

to use depending on what info is available and what is sought

why is g (a = 9.80m/s²) negative given up is positive

because gravity pulls stuff down

Equal vectors

same magnitude (length) and direction regardless of location

Resultant

Sum/Difference of vectors

Formulas for Combining Vectors

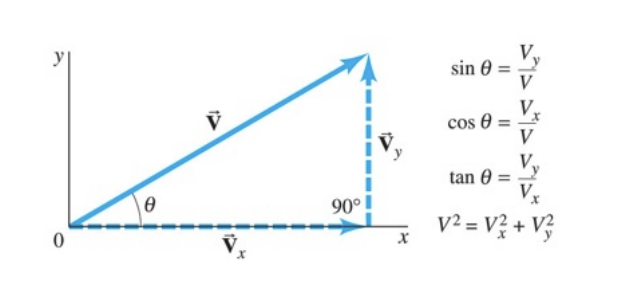
Horizontal Component of Vector

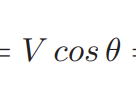
Vertical Component of Vector

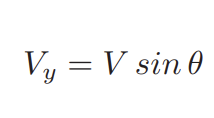
Projectile Motion

treat the x- and y- motions separately by taking components (always resolve initial velocity into components)

Horizontal Motion

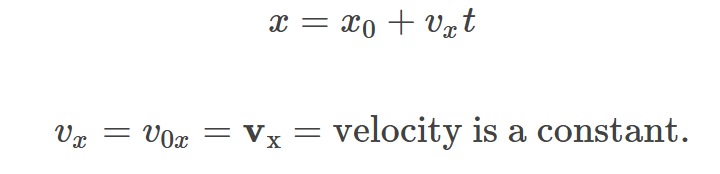
Vertical Motion

finding max height

use equation C

finding time to return to ground

use equation B

finding horizontal distance

use equation A (for x)

negative time to ground

projecting the trajectory into the past when the object would hypothetically have left the ground to have the same eventual trajectory

Resultant Components of 2 Vectors

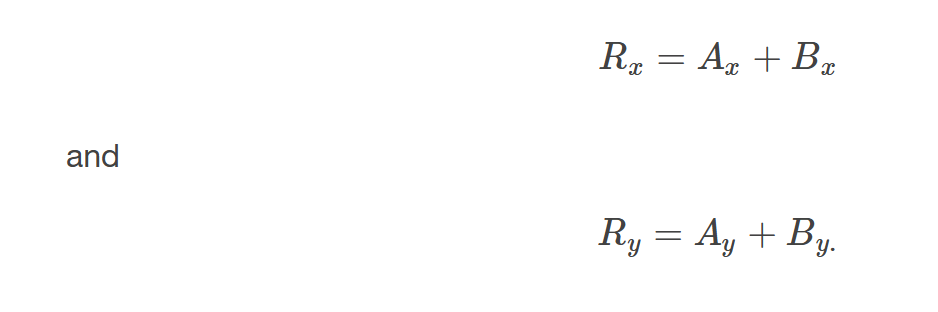
Does horizontal motion change drop rate?

No, 2 objects drop at the same rate from a given height, irrespective of what their initial horizontal velocities were