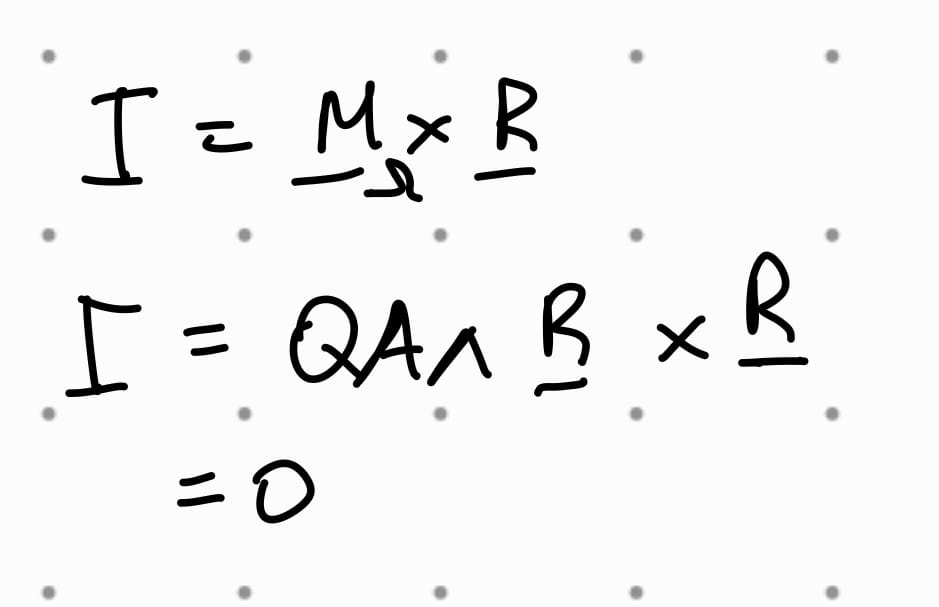0 Meccanica Razionale Capitolo 0: Preliminari
1/42
Earn XP
Description and Tags
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
43 Terms
quali sono le misure scalari, che proprietà hanno
le misure scalari sono misure che si possono esprimere con un solo e semplice numero,
es tempo, massa,
il valore non dipende dalla orientazione rispetto al sdr
che cosa è una matrice
un ente matematico che se moltiplicato (con il prodotto matrice * vettore) restituisce un vettore trasformato
se una matrice viene indentificata come una sorta di funzione che prende un vettore e lo trasforma, esiste una inversa che prende un vettore trasformato e lo raddrizza?
si, la trasposta della matrice stessa
quale è la differenza tra una matrice simmetrica ed una antisimmetrica
una matrice simmetrica equivale alla sua trasposta,
una matrice antisimmetrica invece equivale al negativo della sua trasposta:
A = -AT
quali sono le proprietà di una matrice simmetrica:
A ha tutti gli autovalori positivi
A puo essere diagonalizzata
equivale alla sua trasposta
che cosa vuole dire che una matrice è diagonalizzabile
se A è diagonalizzabile esiste una base formata da autovettori ortonormale, in quella base la matrice si puo esprimere in forma diagonale
come viene definito il prodotto tensoriale di due vettori v e w
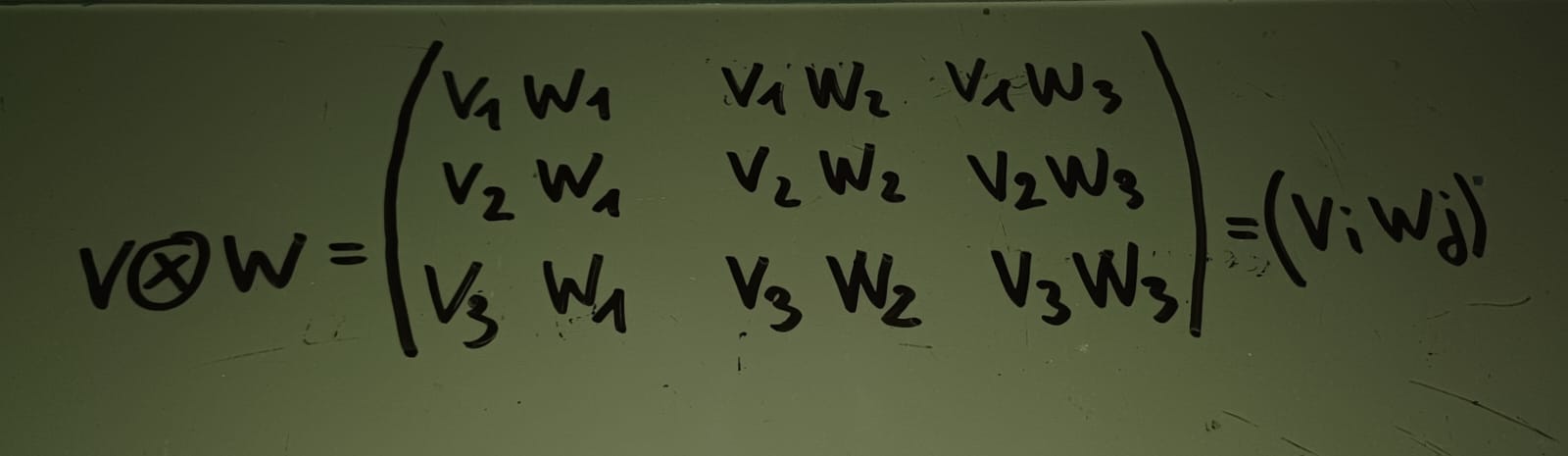
che cosa sono le matrici definite positive / negative, quali criteri si usano per capire se A è definita positiva o negativa
A definita negativa se
Av*v < 0 per ogni v diverso da 0, Av*v = 0 se e solo se v = 0
ha tutti gli autovalori negativi
A definita positiva se
Av x v > 0 per ogni v diverso da 0, Av * v = 0 se e solo se v = 0
ha tutti gli autovalori positivi
determinanti sulla diagonale principale sono tutti positivi
TEO con dimostrazione:
ogni matrice puo essere scomposta in una parte simmetria e antisimmetrica
DIM 1

quale è l’effetto geometrico su un vettore se viene moltiplicato per una matrice
1. positiva
2. negativa
la moltiplicazione di matrice - vettore genera un altro vettore scalato e ruotato
A matrice positiva —> A*v = w con angolo x tra v e w acuto
A matrice def negativa —> A*v = w con angolo x tra v e w tozzo
come è definita la matrice di rotazione (2 Proprietà)
perche deve avere queste due proprietà
DIM 2
una matrice di rotazione ha le seguenti die proprietà:
RT*R = I
det(R) = 1
la

che cosa è il simbolo di Kronoker
una funzione denotata con δ(i,j) associato ad una matrice —> δij
se i = j —> δ = 1
se i diverso da j —> δ = 0
una matrice quadrata di simboli di Kroneker è una matrice identità nxn
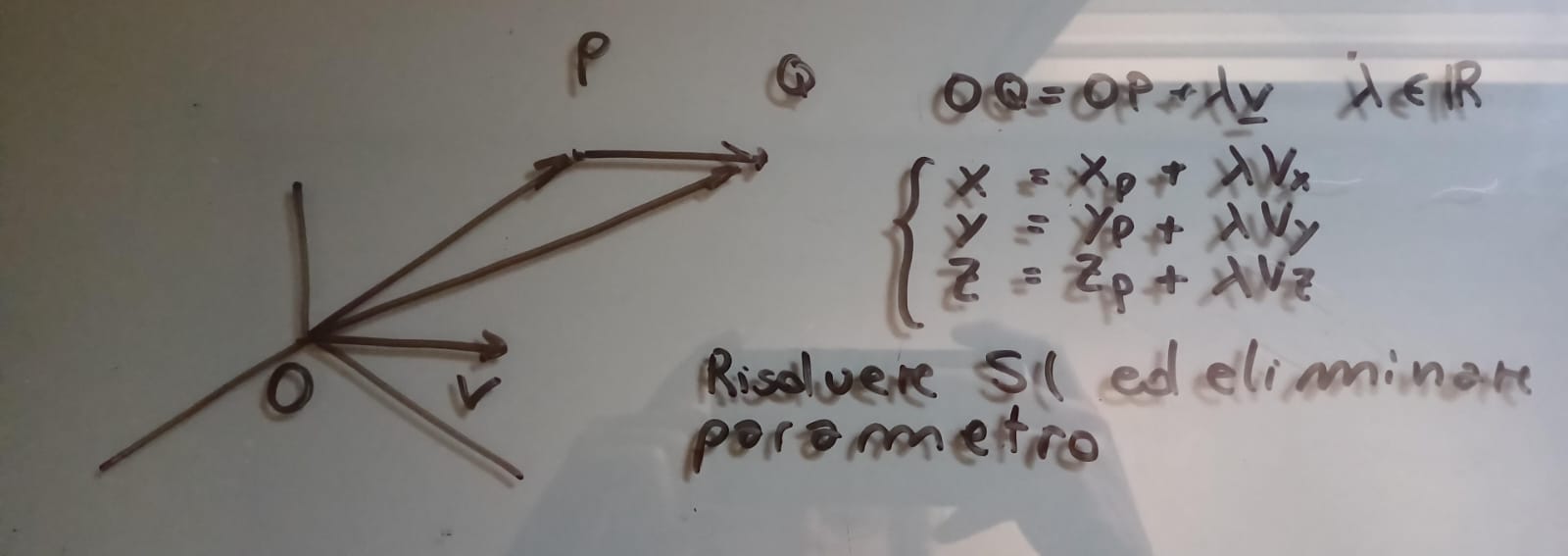
come trovo la equazione di una retta passante per un punto P e parallela ad un vettore v
esercizio
prendo un sistema di riferimento, vale allore che OP = OQ + xv
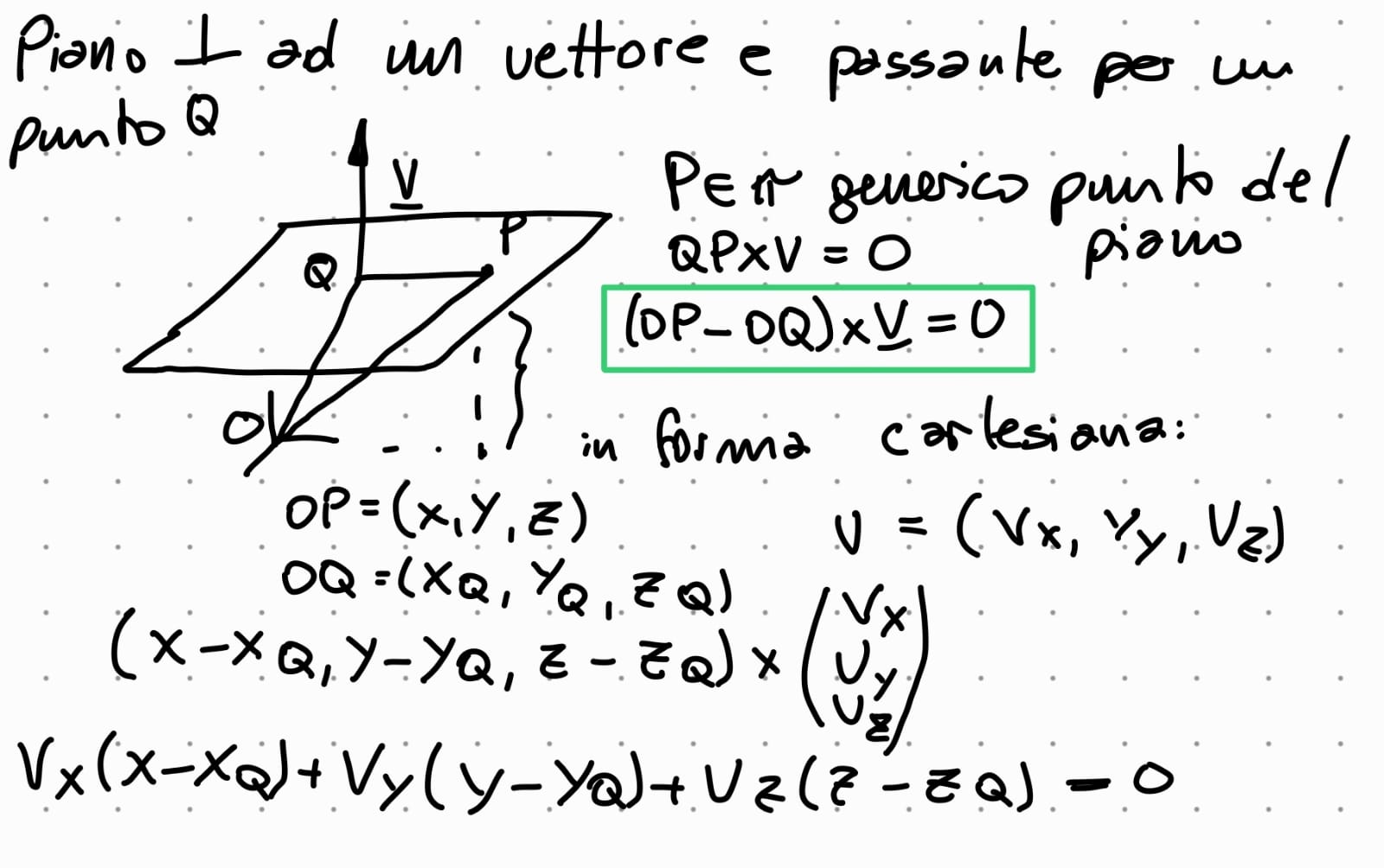
come posso trovare il piano ortognoale ad un vettore e passante per un Punto Q
che cosa sono i vettori applicati
i vettori applicati sono vettori che come punto iniziale non hanno lorigine ma un punto a caso, sono definiti dal vettore v ed un punto iniziale A: va = (v,A)
come è definito il momento Polare,
è un vettore, che direzione ha
quale è una proprietà importante di M spostando v sulla sua retta di azione
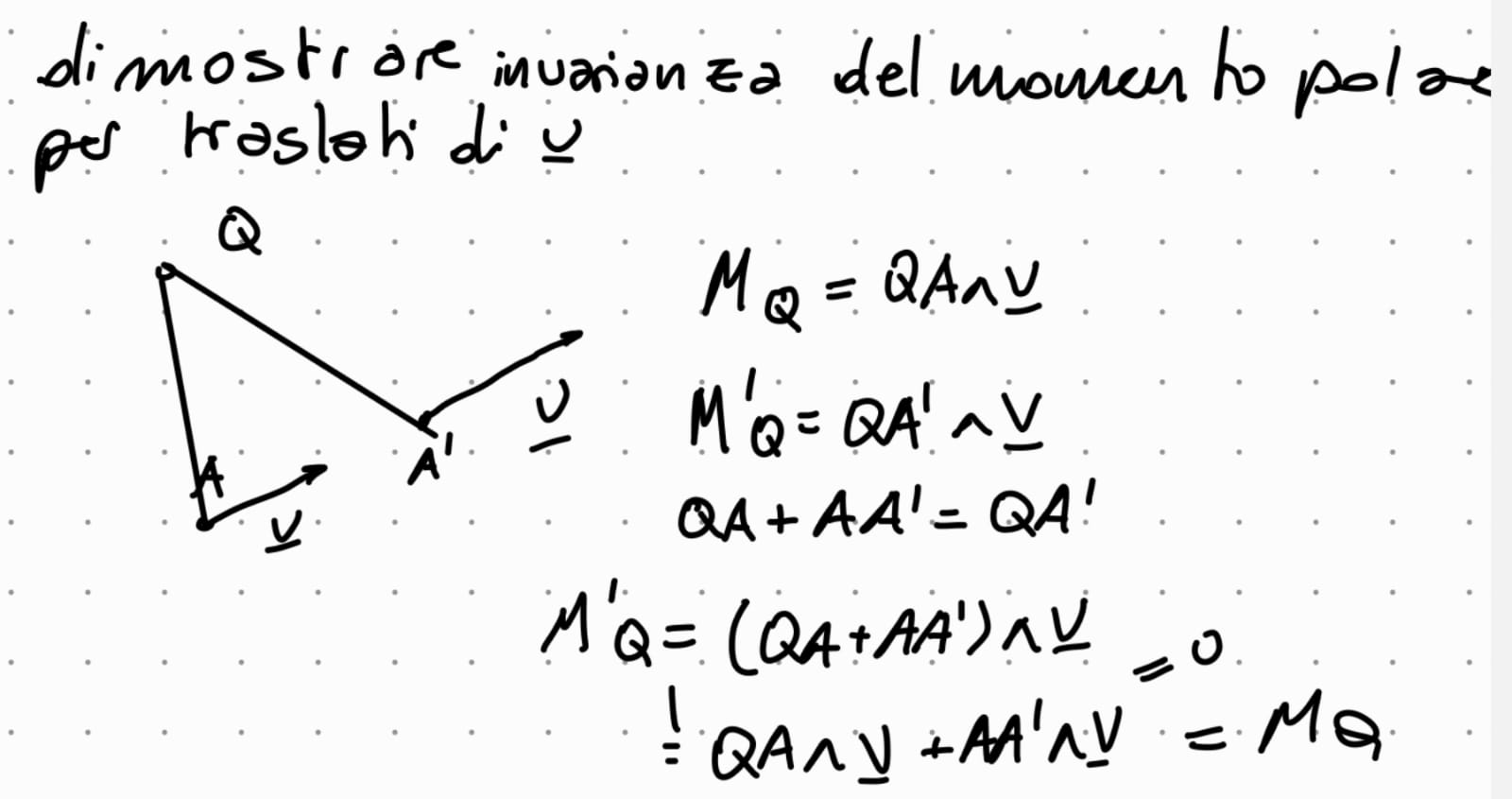
Dimostrare che il momento polare è invariante per traslati di v lungo la sua retta di azione DIM 3
il momento polare di un vettore è definito in funzione di un punto Q, si calcola come
MQ = QA x v dove x è il prodotto vettoriale,
è un vettore ortonormale al piano individuato da QA e v
MQ é invariante per traslati di v lungo la sua retta di azione
come si calcola il momento polare di un sistema di vettori applicati
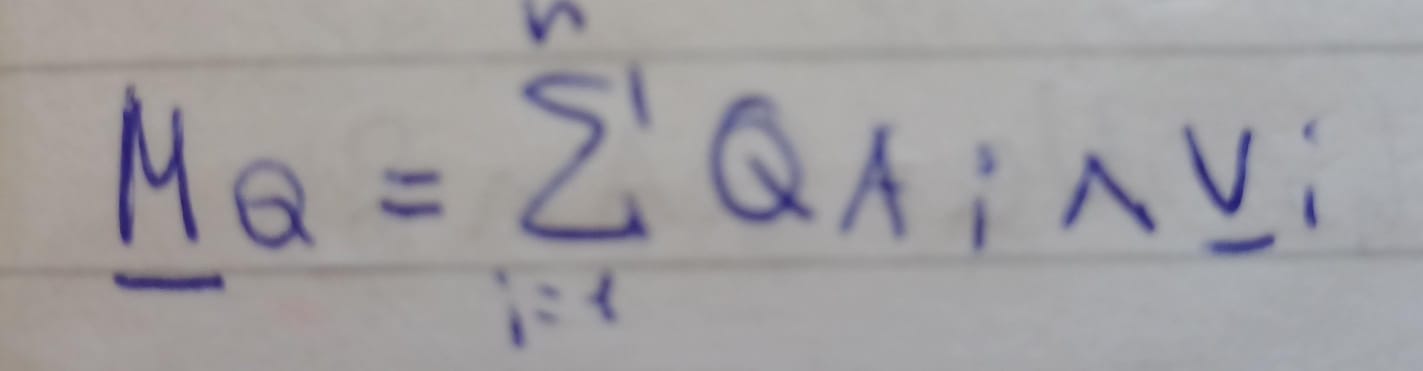
che cosa è l’invariante I
quali sono le 2 Proprietà importanti, dimostrare la prima
I = Mq * R
dove Mq è il momento polare del sistema di vettori applicati rispetto ad un polo q
R è la risultante delle forze
I non dipende dal polo di riduzione q DIM 4
è uno scalare

come si puo scomporre il momento Mq se la risultante delle forze è diversa da 0
si puo scomporre in una componente normale ad R e una parallela ad R
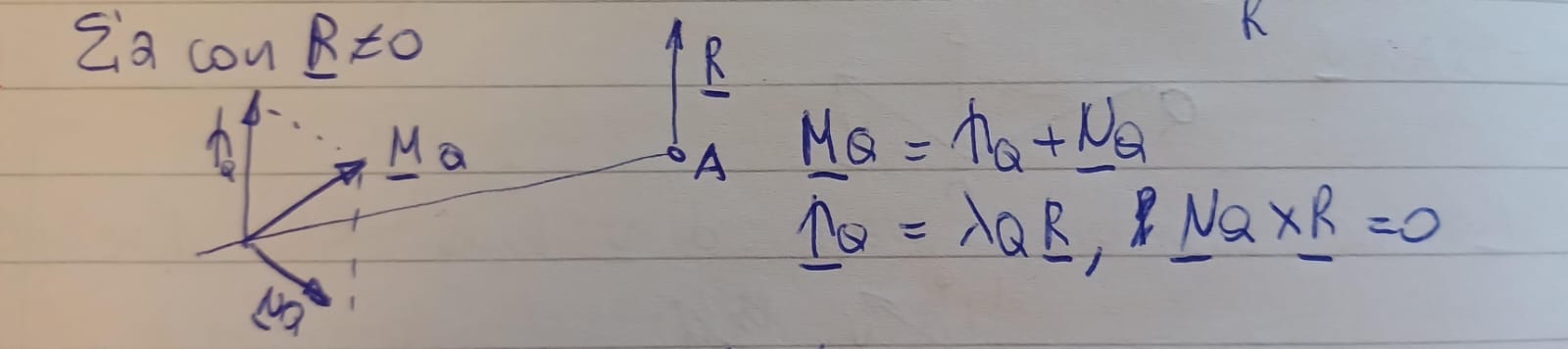
che cosa è la asse centrale.
come è disposta rispetto a R risultante
perche è speciale
DIMOSTRARE la esistenza della asse centrale
DIMOSTRARE che la componente parallela alla risultante del momento è invariante rispetto al polo di riduzione
la asse centrale è un insieme di punti disposti lungo una retta
Parallela a R
se si prende come polo di riduzione il momento ha modulo minimo perche la componente MN normale a R si annulla

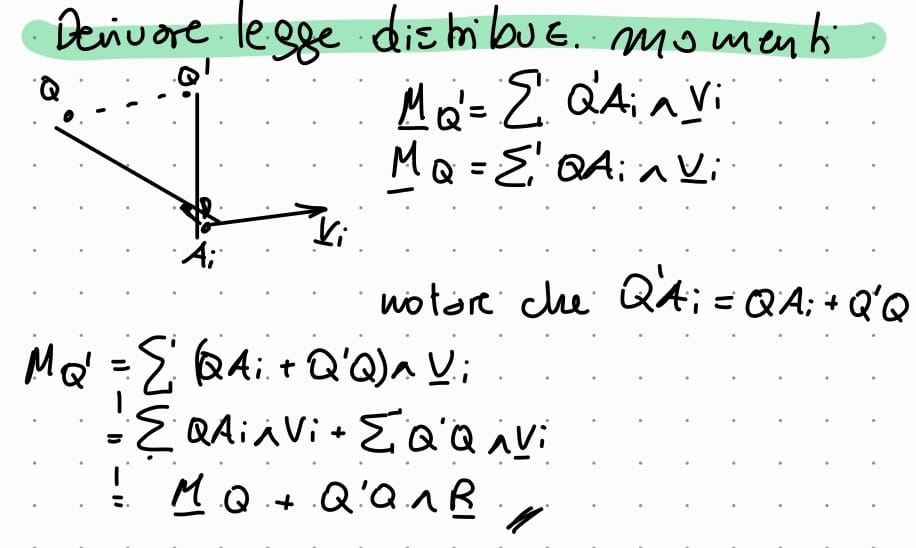
che cosa si chiede la legge della distribuzione dei momenti
e che cosa dice DERIVARE
si chiede come varia il momento risultante di un sistema di vettori applicati al variare del polo di riduzione:
secondo la legge di distribuzione dei momenti, quando il momento di un sistema di vettori applicati è invariante rispetto al polo di riduzione ?
se la risultante è nulla R = 0,
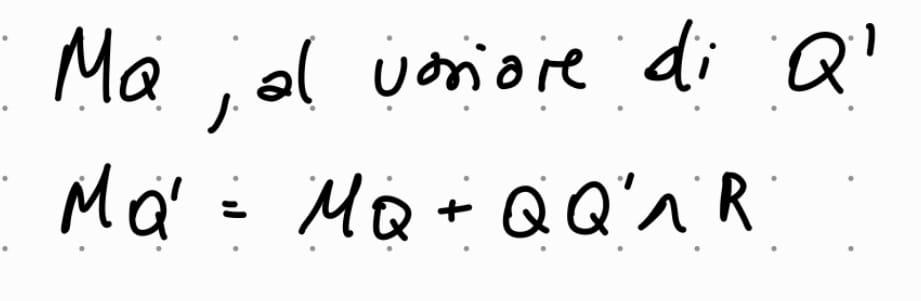
che cosa è il momento assiale Mr di un sistema di vettori applicati ?
rispetto a che cosa viene calcolato ?
quali caratteristiche ha ?
il momento assiale Mr viene calcolato rispetto ad una asse di verso versore u
viene calcolato come il Mr = MQ * u
la cosa piu importante è: per ogni punto Q della retta individuata da u, il momento assiale rimane costante.
DIM 4
il principio della dimostrazione è che partendo con un momento calcolato rispetto ad un polo di riduzione Q elemento della retta “r“ del versore u si ha con
v versore con punto iniziale A
Mq = AQ x v
Se ora calcolo il momento rispetto al punto Q’ elemento della retta r e diverso da Q si ha che Mq’ per la legge di distribuzione dei momenti vale:
Mq’ = AQ’ x v = AQ x v + Q’Q x v
Da notare che AQ x v non cambia al variare di Q’ —> rimane costante per ogni punto Qi sulla retta r. questo si chiama Momento assiale.
la formula sopra riesce ad isolare questa componente di Mq’ perchè
(Q’Q x v) * u = 0 dato che Q’Q x v genera un vettore ortogonale al piano dove giaciono i due vettori —> (Q’Q x v) è ortogonale a u e percio il prodotto scalare si annulla!
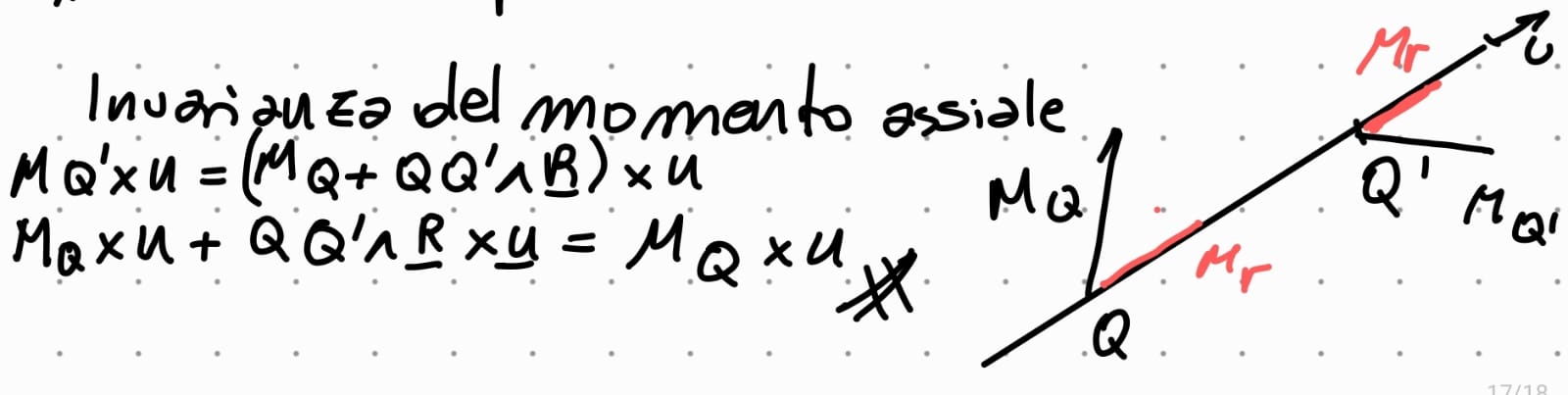
enunciare il teorema di Varignon e Dimostrazione
Un sistema di vettori applicati in uno stesso punto, o tali che le loro rette d’azione passino per lo stesso punto, ha momento risultante uguale al momento del vettore risultante applicato in quel punto
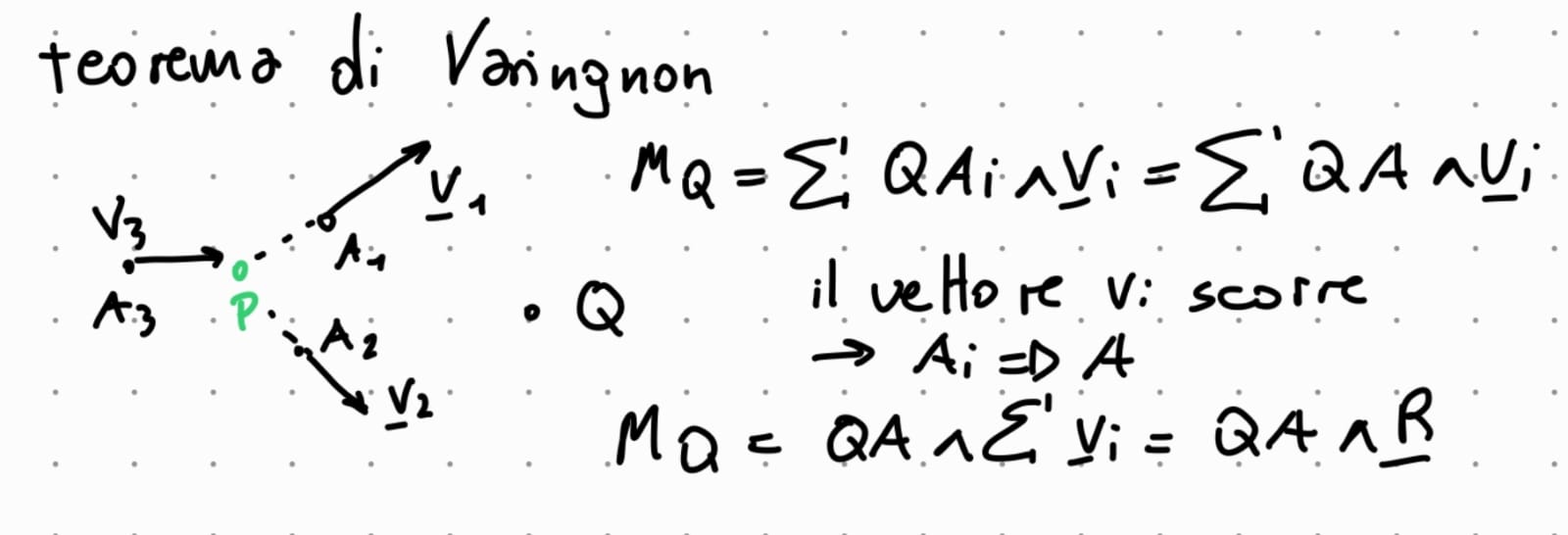
come viene definita una COPPIA
una coppia è un sistema di due vettori applicati a risultante nulla
quali sono le caratteristiche di una coppia
quando una coppia ha momento risultante nullo
Una coppia è composta da due vettori a risultante nulla, il momento della coppia è invariante dalla scelta del polo di riduzione
una coppia ha risultatnte nullo ed è composta da due vettori, per forza i due vettori devono avere la stessa direzione ma orientamento diverso e essere uguali in modulo
una coppia ha momento risultante nullo quando i due vettori della coppia hanno la stessa retta di azione e percio braccio nullo
quale è la condizione affineche il momento di un sistema di vettori applicati sia indipendente dalla scelta del polo di riduzione?
è una condizinoe neccessaria, sufficiente o entrame?
Per un sistema di vettoria applicati con risultante nulla il momento risultante non dipende dal polo di riduzione. è una condizione sufficiente e necessaria
come si calcola il momento di una coppia
|Mc| = d*|v| dove di è il braccio
Mc = b*v*u dove u è il versore normale al piano su cui giace la coppia
perche la invariante si chiama invariante, che cosa succede quando si annulla
Dimostrare!
L’invariante si chiama invariante perche non dipende dal polo di riduzione scelto
DIM 6(p. 25 pdf)
quando linvariante I = M * R = 0 si annulla vuole dire che M e R sono ortogonali
es in un sistema di vettori paralleli

che cosa sono le operazioni elementari, che caratteristiche hanno
aggionta / togliere coppia di vettori a braccio nullo
sostituzione di piu vettori applicati nello stesso punto con la risultante di tali vettori applicata sempre nello stesso punto; o viceversa la scomposizione di un vettore in piu vettori con risultante equivalente al vettore iniziale
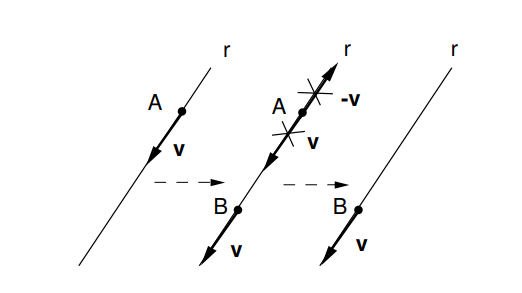
Segue dalle due definizioni sopra che si puo spostare un vettore applicato lungo la sua retta di azione
Caratteristica:
le operazioni elementari non cambiano ne il momento risultante ne la risultante del sistema di vettori
che cosa sono sistemi di vettori applicati ridicubili
due sistemi di di vettori applicati di dicono riducibili se si riesce a passare da un sistema di vettori applicati ad un altro con operazioni elementari
che cosa è un sistema di vettori applicati riducibile a zero (= sistema in equilibrio)
un sistema che tramie operazioni elementari si riesce a ridurre a coppie con braccio nullo
Teorema di Riducibilità (no dimostrazione ) sono tre punti
Un sistema di vettori applicati di risultante R e momento risultante MQ calcolato rispetto a un polo Q è riducibile ad un solo vettore R applicato in Q e ad una coppia di momento MQ.
un qualunque sistema di vettori applicati si puo riscrivere come sistema di 3 v.a.:
{(A1,v1), (A2,v2), (A3,v3)}un qualunque sistema di 3 v.a. è riducibile a 2 v.a.:
{(A1,v1),(A2,v2)}un qualunque sistema di 2 v.a. è riducibile a 1 v.a. e una coppia
{(A,v), + coppia}, in questo caso R = v e M = momento della coppia
che cosa dice il teorema di equivalenza (no dimostrazione)
in particolare che cosa dice riguardo ad un sistema di vettori riducibile a zero
La condizione Sufficiente e Necessaria per la equivalenza di due sistemi di vettori applicati chiamati S e S’
R = R’
Mo = Mo’ per ogni o
Nel caso particolare la condizione sufficiente e necessaria per un sistema riducibile a zero:
condizione necessaria e sufficiente: R = 0 Mo = 0 per ogni “o“
a che cosa si puo ridurre un sistema di vettori applicati con R ≠ 0 e I ≠ 0 per:
A un polo qualsiasi, A polo della asse centrale
A polo qualsiasi: v.a. + coppia
A polo asse di centrale: v.a + coppia di modulo minimo
a che cosa si puo ridurre un sistema di vettori applicati con R ≠ 0 e I = 0 per:
A un polo qualsiasi, A polo della asse centrale
A polo qualsiasi: v.a. + coppia
A polo di asse centrale: v.a + nessun momento, che in questo caso è nullo
DIM M = I/R² * R = 0
a che cosa si puo ridurre un sistema di vettori applicati con R = 0 e M ≠ 0 per:
A un polo qualsiasi, A polo della asse centrale
A polo qualsiasi: Coppia
A polo di asse centrale: non esiste asse centrale
a che cosa si puo ridurre un sistema di vettori applicati con R = 0 e M = 0 per:
A un polo qualsiasi, A polo della asse centrale
A polo qualsiasi: coppia di vettori a braccio nullo
A polo di asse centrale: non esiste asse centrale
che cosa è un sistema di vettori applicati piano
quanto vale Invariante per un sistema piano:
un sistema in cui tutte le rette di azione dei vettori appartengono ad un piano, il piano si dice piano del sistema
L’invariante per un sistema piano è nullo dato che il momento rispetto ad un qualunque polo sul piano è ortogonale al piano stesso —> il prodotto scalare tra R (parallelo al piano) e M è nullo
che cosa è un sistema di vettori paralleli
quanto vale Invariante per sistemi a vettori paralleli
un sistema si dice a vettori parallele se tutte le rette di azione dei vari vettori sono parallele tra loro
Linvariante è nullo dato che il momento calcolato per ogni punto è ortogonale a R
la asse centrale invece è una retta parallela e coincidente R
che cosa è il centro di un sistema di vettori paralleli, come si calcola
Dimostrazione DIM 6
lasse centale di un sistema di vettori applicati paralleli è concorde con la direzine dei vettori. se ora si fanno ruotare tutti i vettori di un certo e dello stesso angolo ci sara un nuovo asse centrale, questo si va a intersecare con quello di prima. facendo la stessa operazione piu volte si trova il punto di intersezinoe di tutte le assi centrali del sistema di vettori applicati paralleli.
il centro di un sistema di vettori paralleli è la intersezinoe di tutti gli assi centrali calcolati per il sistema se si fanno ruotare i vettori
la formula per lasse centrale è

scrivere la equazione parametrice per l’asse centrale
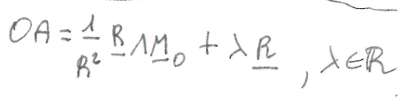
dimostrare che la invariante di di un sistema di vettori paralelli è nulla