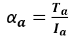Biomechanics Angular Kinetics In Class Notes

Module 8

What is Angular Power?

The rate of change in angular work​

Is power a vector or a scalar ?

scalar

What are the units of power?

watts (J/s)

Equation for angular power? 

torque and angular velocity 

What is Muscle Power determined by

calculating net torque at the joint and angular velocity of the joint

Muscle Power equation?

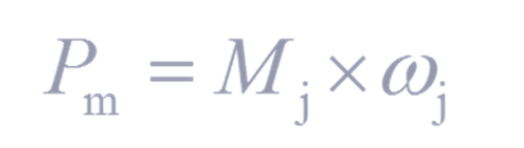
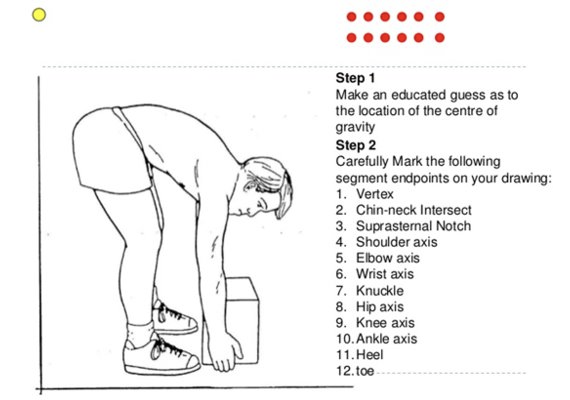
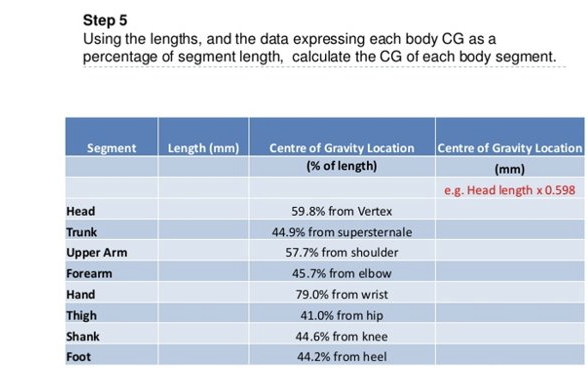
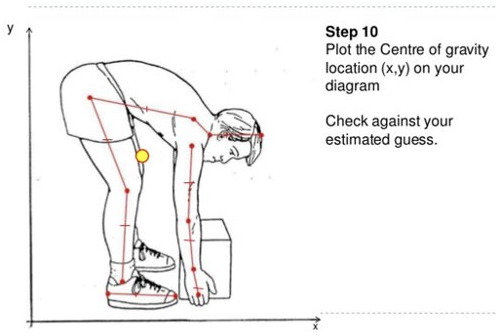
The segmental method is the estimation of the

location of the body’s total center of gravity

• each individual segment has its own center of gravity

• standard set of values for mass ratio and center of gravity for each body segment is used

• Cartesian coordinates are obtained for each segment (tells us our x,y)

What does segmental method steps look like?

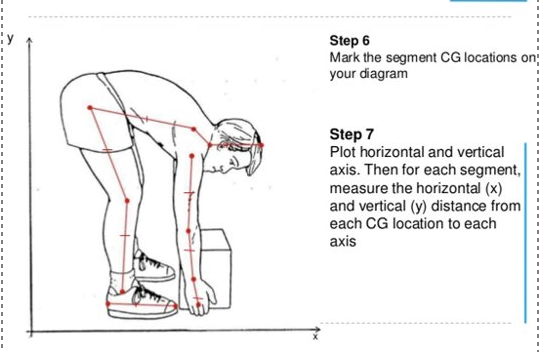
During Newtons First Law (Law of Inertia) during angular pov

A body continues in a state of rest or uniform rotation about its axis unless acted upon by an external torque​

Eccentric force: force applied off-center​

Forces generated by the muscle​

Angular inertia​

Mass distribution about an axis of rotation (i.e., joint) may be altered by changing the limb position (i.e., bringing the limb in closer to the axis of rotation by flexing at a joint​

ex ) constant angular velocity: fan spinning

ex) at rest: fan not spinning

Many concepts of angular inertia are similar to ?

linear kinetics

Linear Inertia is 

resistance of a body to changing motion

Angular Inertia is the property of

an object to resists changes in its angular motion

• its not just dependent on mass

Center of mass can

move

Moment of Inertia quantifies

how an objects mass is distributed relative to a specific axis of rotation

During moment of inertia, a mass that is farther from the axis has

more angular resistance

During moment of inertia, a mass that is closer to the axis has

less angular resistance

Moment of inertia considers each individual

mass particle

Moment of Inertia mathematical equation?

Radius of gyration is the

radial distance of that point, from the axis of rotation at which the whole mass of the body is supposed to be concentrated

• Simpler approach to consider mass distribution​

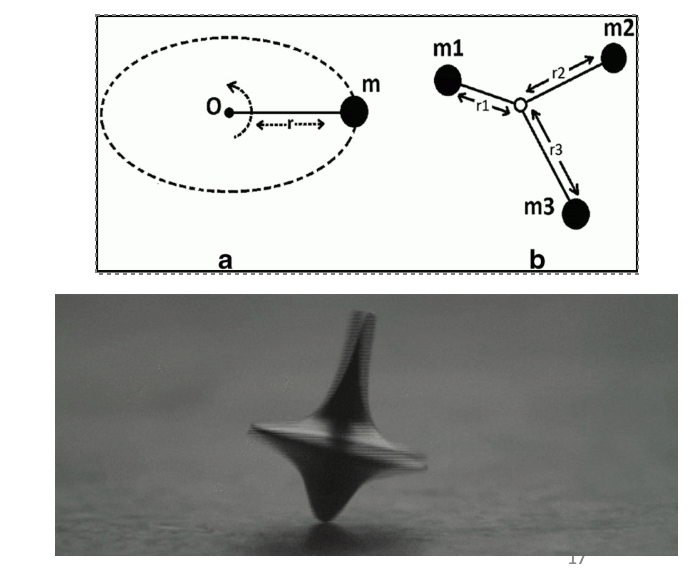
Rotating body’s resistance t angular acceleration or deceleration is equal to

• Product of the mass ​

• Square of its perpendicular distance from the axis of rotation

Moment of inertia depends on?

• mass

• distribution of the mass

Moment of inertia determines the torque needed for

a desired angular acceleration about a rotational axis

• Distribution has a greater effect ​

• Double the mass = 2 × Inertia would double

• Double the radius of gyration = 4 × Inertia would quadruple) because the r is squared!

Moment of inertia about eccentric axes says

Not all rotation occurs around the center of gravity

Eccentric axis → implement axis not passing through the center of gravity​

• The performer holds the “grip” or “end” of the implement, not the center of gravity. EX) Bat, hammer, stick, racket​

• The new axis is called → parallel axis​

• Mass farther from the axis of rotation means I is greater​

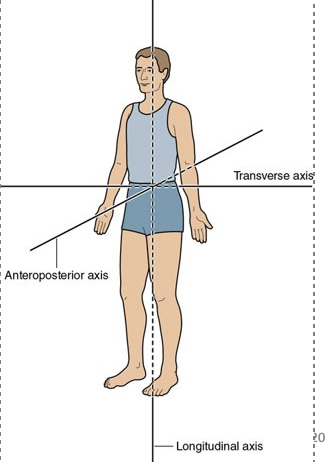
What are the principle axes in the human body?

Anteroposterior (cartwheel)​

Transverse (somersault)​

Longitudinal (twist)​

The moment of inertia around each axis depends on?

the position or orientation of the limbs relative to the axis

Manipulating the moments of inertia of the human body is when you alter the

relative angle at a joint or joints changes / by changing the mass distribution around a joint axis

• Sprinter’s leg during recovery phase​

• Swinging a tool​

​Altering the relative angle at many joints changes the Icg by changing the mass distribution around the cg​

• Arm use by figure skaters when spinning​

• Tuck versus layout position of divers and gymnasts in somersaults​

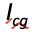
moment of inertia center of gravity

Angular momentum quantifies the

angular motion of an object, describing both current state of motion and resistance to changing motion

Angular momentum is a vector or scalar?

vector

Magnitude: Iω (units: kg∙m²/s)​

Direction: same as direction of ω​ (Follows right-hand rule conventions)

Tangential velocity (Vt) and Moment of Inertia (I) is greater with

longer radius

The trade-off when choosing length of swinging implement is

Ease of swing versus effectiveness of velocity achieved​

• Bat, stick, racket, hammer​

For angular momentum of the human body, frequently many limbs rotate at

different ωs

• Ha of body is the sum of angular momenta of individual segments

(H is angular momentum)

For Newtons First Law, (Angular Interpretation), angular momentum of an object remains constant unless

a net external torque acts on it

• If Is are constant, ω is constant

For Newtons First Law, (Angular Interpretation), for a rigid projectile, gravity is the

only external force

• Weight acts through the cg​

• Weight has no moment arm around the cg​

• No external force on body​

• Weight creates no external torque on a projectile​

​

Newtons First Law (Angular Interpretation) : H (product of l and ω) remains constant unless

a net external torque acts on the rotating body

Newtons First Law (Angular Interpretation): Human body is a system of 

rigid links with a modifiable I

• With H constant (no external torque applied)​

       -Increase in I, there must be a proportional decrease in ω ​

       -Decrease in I, there must be a proportional increase in ω​

• For faster spin, reduce I (tuck, arms in)​

• For slower spin, increase I (layout, arms out)​

When talking about Controlling ω of Limbs or Trunk​, Hcg remains

constant while a projectile

• Individual segments have Hi/cg from I and ω

Repositioning one or more segments of a body must be countered by

repositioning one or more segments in the opposite direction to maintain constant Hcg

• Repositioning means changing ω

Newton’s Second Law: Angular Interpretation​, if a net external torque acts on a body, the body will angularly

accelerate in the direction of the net external torque

Newton’s Second Law: Angular Interpretation, acceleration will be

• Directly proportional to the torque ​

• Inversely proportional to its moment of inertia​

It is similar to newtons second law for linear motion

Newton’s Second Law: Angular Interpretation​, angularly accelerate is a

change in angular momentum

the change in angular momentum of an object is proportional to the

net external torque exerted on it and the changes is in the direction of the net external torque

• Torquea and ωa have same sign: Ha increases​

• Torquea and ωa have opposite sign: Ha decreases

If I changes when T applied, change in ω is 

greater 

Newton’s Third Law: Angular Interpretation, for every torque exerted by one object on another, the other object exerts an

equal torque back on the first object but in the opposite direction

Newton’s Third Law: Angular Interpretation​, torque on each body is of equal

magnitude, not the effect