Physic Notes -> Newton's Laws of Motion
1/30
Earn XP
Description and Tags
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
31 Terms
First Law of Motion
Unless we apply an external influence on an object, an object at rest will remain at rest, and an object in motion will continue with uniform velocity in a straight line.
Inertia
The tendency of an object to resist changes in its state of motion, maintaining its velocity unless acted upon by an external action.
Static Inertia
The property of an object that causes it to remain at rest unless acted upon by an external action.
Kinetic Inertia
The property of an object that causes it to continue moving at a constant velocity unless acted upon by an external action.
Force
The external influence/action that changed the inertia of a body.
Frame of Reference
The perspective, described by a coordinate system, of analysis; the viewer
Inertial Frame of Reference
A reference frame where its motion is either at rest or moving at a constant speed in a straight line; note that all of Newton’s Laws of Motion can apply in these situations.
Non-Inertial Frame of Reference
A reference frame where its motion is described as an acceleration or deceleration; note that all of Newton’s Laws of Motion does not apply in these situations.
Differences in Inertial Frames of References
As all inertial frames of reference are the same, we can say that there is no ABSOLUTE inertial frame of motion; all motion is relative.
Second Law of Motion
The force is proportional to the rate of change of momentum.
Momentum
p = m(mass) x v(velocity)
The force is proportional to the rate of change of momentum.
F ∝ ΔP/ΔT
k → constant of proportionality
F = k x ΔP/ΔT
If unit force is defined, in any unit of measurement system, as a force that causes a unit change in momentum in unit time, thus k=1.
F = ΔP/ΔT
When the mass is constant:
F = dp/dt
F = d/dt x (mv)
→ As Mass is constant
F = m (dv/dt)
Thus, F = ma
F = ΔP/ΔT
When the velocity is constant:
F = dp/dt
F = d/dt x (mv)
→ As Velocity is constant
Thus, F = v (dm/dt)
F = ΔP/ΔT
When both variables are changing:
F = dp/dt
F = d/dt x (m x v)
→ Use product Rule
F = m x dv/dt + v x dm/dt
Rocket Equation
When a rocket lets go of the liquid fuel, it causes the mass to change constantly, thus no longer constant; while the rocket moves away from Earth, the air resistance and gravitational pull become less and less, therefore less force is needed, so the velocity is changing. In this case, use the product rule:
Third Law of Motion
Every Action has its equal and opposite reaction.
Components of the Third Law
Action → object 1 applies force on object 2
Reaction → object 2 reacts by applying the force onto 1 instantaneously
Equal → thus, we can say that the force applied from object 1 to 2 is equal to the force from object 2 to 1.
Free Body Diagram
Identify each body in ACTION
We take each body out from its environment and then day the FBD for each body separately, essentially detaching them.
In the FBD process, we only draw the forces that act on the body itself; never ever draw the forces that the body applies to others.
Then apply New’s Law of Motion on each body.
Usefulness of the FBD
Able to:
Visualize all external forces acting on an object.
Simplify complex problems by isolating an object from its environment.
Apply Newton's Laws of Motion to analyze motion or equilibrium.
Determine the net force and acceleration of an object clearly.
Gravity
Action at a Distance
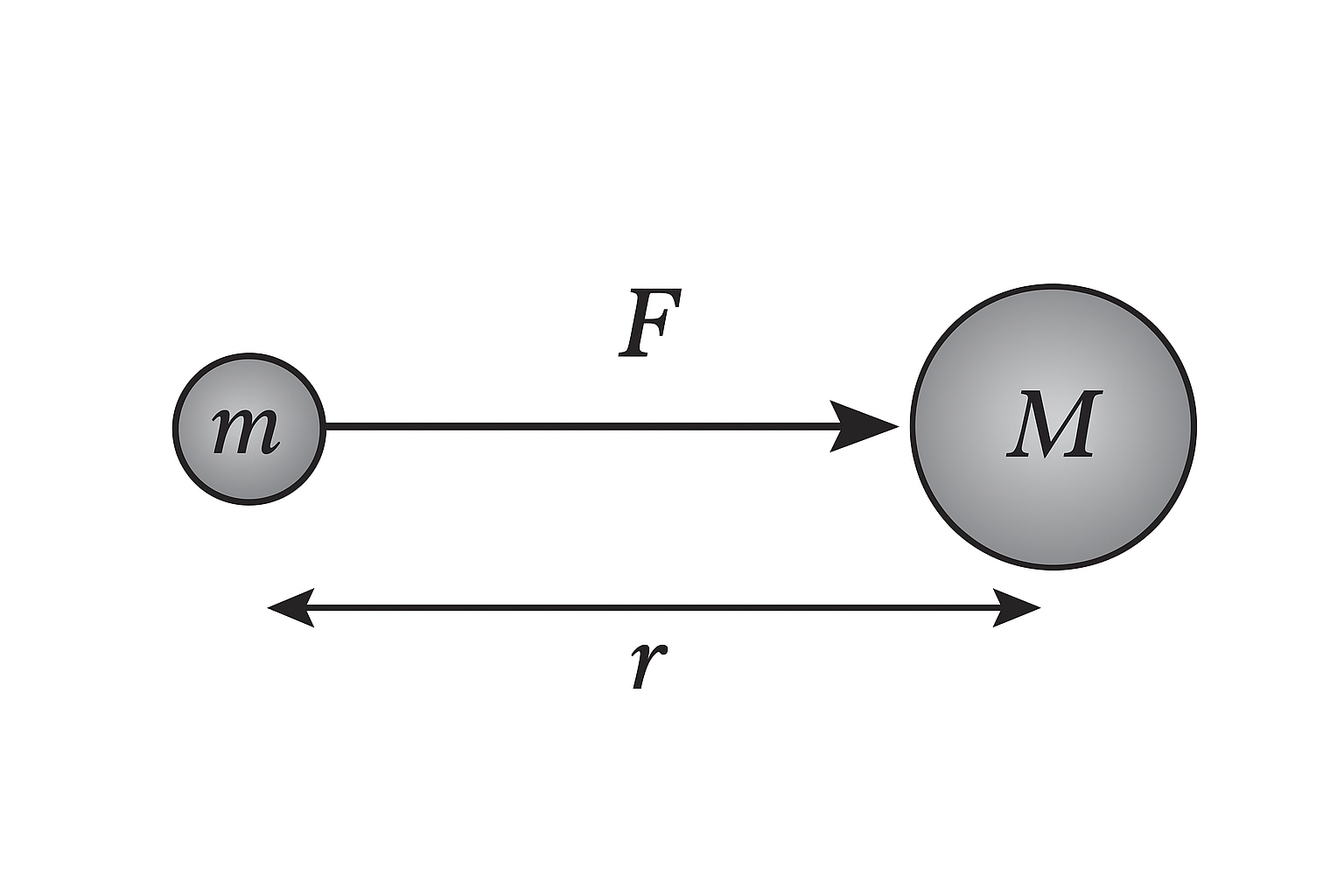
Two bodies of masses, m & M, separated by the distance of r, that attract each other with the gravitational force F
F ∝ mM
Force varies with the product of the masses of the two bodies
F ∝ 1/r2
Force inversely varies with the square of the distance between the two bodies
Joint Law Variation
Mathematical relationship where one quantity is directly proportional to two or more other quantities
Newton’s Law of Gravity
F ∝ mM/r2
F = G( mM/r2)
Newton’s Law of Gravity
G
When turning the proportion of Newton’s Law of Gravity, the k that is usually multiplied to the proportion becomes G, the gravitational constant, in order to tranform the intial proportion into an equation.
Gravitational Acceleration
On Earth, the gravitational acceleration remains as constant