pure

find value of k in y= k(x-2)(x-4)

-substitute in values of x and y from graph

derivative of 2^x

(ln2)(2^x)

find quadratic equation lonking H with x

H= a(x+b)(x+c)

proof by contradiction

a rational number is a number in the form a/b where a and b are integers with no common factors (a/b is in its simplest form)

arithmetic equations

Un = a + (n-1)d

sum: n/2(2a+ (n-1)d)

n/2(a+L)

proving arithmatic sequence sum….

a + (a+d) + (a+2d)…a+(n-1)d

reverse: a+ (n-1)d + a+(2d) + a+d +a

2sum :ADD TOGETHER: 2a + (n-1)d

sum:

geometric sequene equation

un= a x r^n-1

a(1-r^n)/1-r

proving sum of geometric sequence

Sn: a + ar + ar²…+ar^n-1

multiply by r: ar + ar²…+ar^n

subtract both equation: a+ar^n = a(1+r^n)

Sn(1-r) = a(1-r^n)

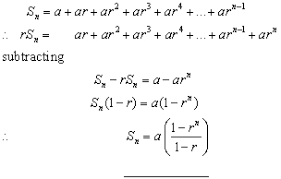
convergent geometric series equation (sum to infinity)

a/1-r

convergent if r<1

inequality set notation

{x:x<5}U{x:x>10}

area of segment

1/2r²x - r²sinx

x is angle

area of sector

1/2r² x angle

only applies when angle is in radians, not degrees

arc sector length

angle x radius

sine rule

a/sin(A) = b/sin(B) = c/sin(C)

cosine rule

a²=b²+c² -2bcsin(a)

cast diagrams

cos all sin tan

Area of a rhombus

Cross section x cross section /2

Prove using vectors that a shape is a trapezium

Has 2 parallel lines so vectors will be factors of each other

3D vectors: find angle that vector a=2i-3j-k makes with +ve x axis

cosX = x/ magnitude of a

magnitude of a is hypotenuse

binomial expansion formula for (1+x)^n

1+nx+ n(n-1)/2! (x²) +n(n-1)(n-1)/3!(x³)

if its (4+x)^n, factor our 4 to make it 4^n(1+1/4x)

-expansion valid if [x]<1
-or [x]<4

x should be as close as possible to 0

exponential graph

Trig modelling- find time for one complete revolution

Find consecutive times that tourist is at certain height, e.g. H=0, pi, 3pi

prove that square of any natural number is a multiple of 3 or 1 more than a multiple of 3

natural number can be expressed as 3k, 3k+1, 3k+2

exponential model equation

y=Ae^kx

OR y=a.b^x

model is reliable if value of y~ their value (approximately equal)

cylinder: volume and surface are

pi x r² x h

circumference x h + 2 pi r^ 2(top and botto. surfaces )

circumference = 2pi x r

which functions have an inverse

one-to-one

because for many-to-one functions, line intercepts curve more than once

irrational numbers

root 2, root 3