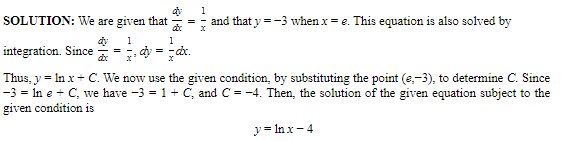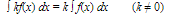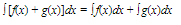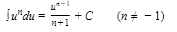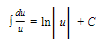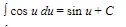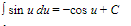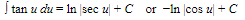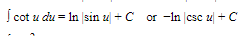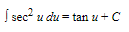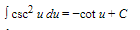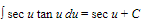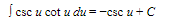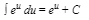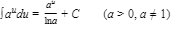Chapter 5: Antidifferentiation

A. Antiderivatives

• The antiderivative or indefinite integral of a function f(x) is a function F(x) whose derivative is f(x).

• Since the derivative of a constant equals zero, the antiderivative of f(x) is not unique; that is, if F(x) is an integral of f(x), then so is F(x) + C, where C is any constant.

• The arbitrary constant C is called the constant of integration.

• The indefinite integral of f(x) is written as ∫ f(x) dx; thus

  

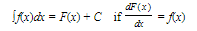
• The function f(x) is called the integrand.

• The Mean Value Theorem can be used to show that, if two functions have the same derivative on an interval, then they differ at most by a constant; that is, if

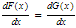
  then

  F(x) − G(x) = C(C is a constant)

  \

B. Basic Formulas

\
15.
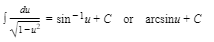
16.

\
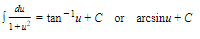
17.

\

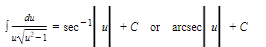
C. Integration by Partial Fractions

• The method of partial fractions makes it possible to express a rational function f(x)/g(x) as a sum of simpler fractions.

• Here f(x) and g (x) are real polynomials in x and it is assumed that f(x)/g(x) is a proper fraction; that is, that f(x) is of lower degree than g(x).

• If not, we divide f(x) by g(x) to express the given rational function as the sum of a polynomial and a proper rational function. Thus,

  

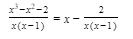
where the fraction on the right is proper

• Theoretically, every real polynomial can be expressed as a product of (powers of) real linear factors and (powers of) real quadratic factors.
• In the following, the capital letters denote constants to be determined.
• We consider only nonrepeating linear factors. For each distinct linear factor (x − a) of g(x) we set up one partial fraction of the type A/x−a.
• The techniques for determining the unknown constants are illustrated in the following examples.

\
Example:

Find ∫ x cos x dx.

SOLUTION:

We let u = x and dv = cos x dx.

Then du = dx and v = sin x. Thus, the Parts Formula yields

∫ x cos x dx = x sin x − ∫ sin x dx = x sin x + cos x + C

\

The Tic-Tac-Toe Method

This method of integrating is extremely useful when repeated integration by parts is necessary. To integrate ∫ u(x)v(x) dx, we construct a table as follows:

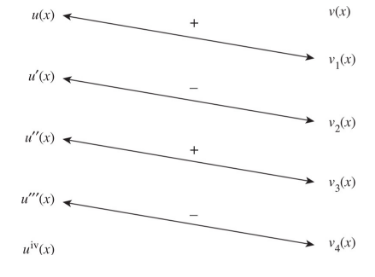
• Here the column at the left contains the successive derivatives of u(x).
• The column at the right contains the successive antiderivatives of v(x) (always with C = 0); that is, v(x) is the antiderivative of v(x), v2(x) is the antiderivative of v1(x), and so on.
• The diagonal arrows join the pairs of factors whose products form the successive terms of the desired integral; above each arrow is the sign of that term. By the tic-tac-toe method,

∫ u(x)v(x)dx = u(x)v1(x) − u′(x)v2(x) + u″(x)v3(x) − u″′(x)v4(x) + . . . .

\
Example:

To integrate ∫ x4 cos x dx by the tic-tac-toe method, we let u(x) = x4 and v(x) = cos x, and get the following table:

\

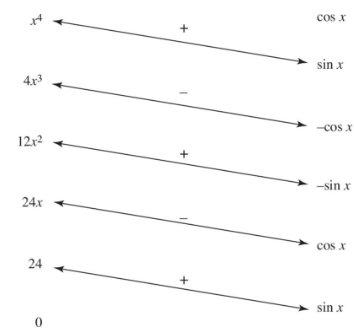
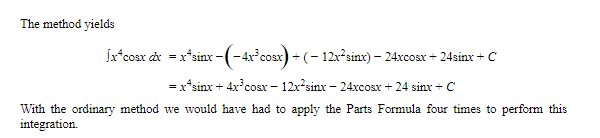
E. Applications of Antiderivatives: Differential Equations

The following examples show how we use given conditions to determine constants of integration.

\
Example :

Find a curve whose slope at each point (x,y) equals the reciprocal of the x-value if the curve contains the point (e,−3).

SOLUTION:

\