Matematika SNBT

Pers Kuadrat

X1+X2

-b/a

pers kuadrat

X1.X2

c/a

hasil = waktu . merupakan perbandingan?

Perbandingan senilai

hasil = tenaga . merupakan perbandingan?

Perbandingan senilai

waktu = tenaga . merupakan perbandingan?

Perbandingan terbalik

Baris dan deret

Rumus Suku ke-n (aritmatika)

Un = a+(n-1)b

Baris dan Deret

Rumus jumlah suku ke-n (aritmatika)

Sn = n/2 (2a+(n-1)b)

Sn = n/2 (a+Un)

Baris dan Deret

Rumus mencari Suku tengah

Ut = a+suku terakhir /2

Baris dan Deret

Rumus Suku ke-n (geometri)

Un = ar^n-1

Baris dan Deret

Rumus jumlah suku ke-n (geometri)

Sn = a/1-r .(1-r^n)

Rumus deret tak hingga

S~= a/1-r

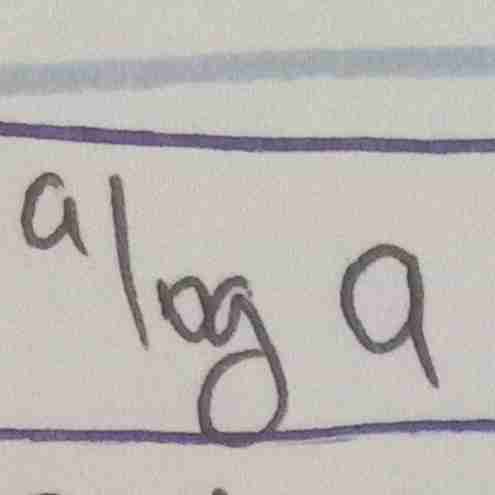
sifat logaritma

1

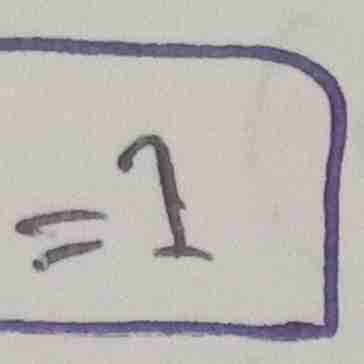
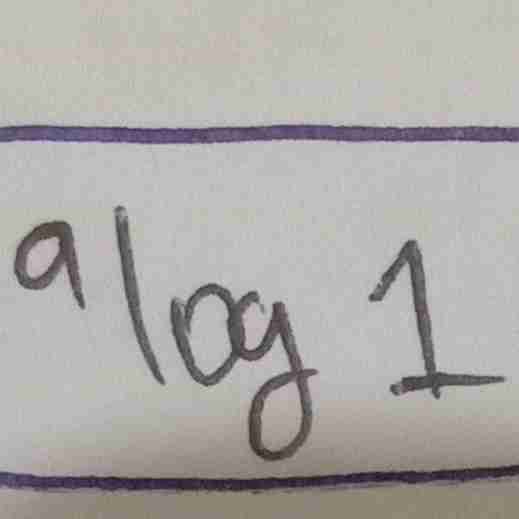
a

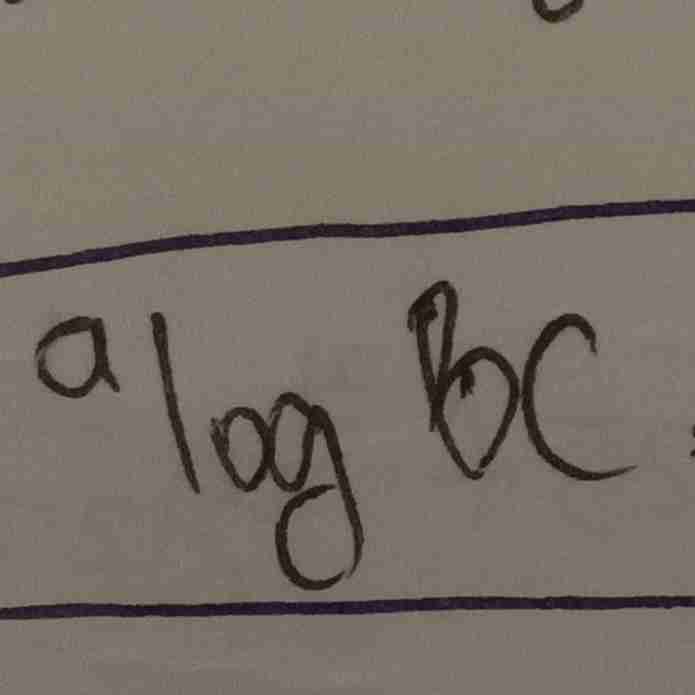
sifat logaritma

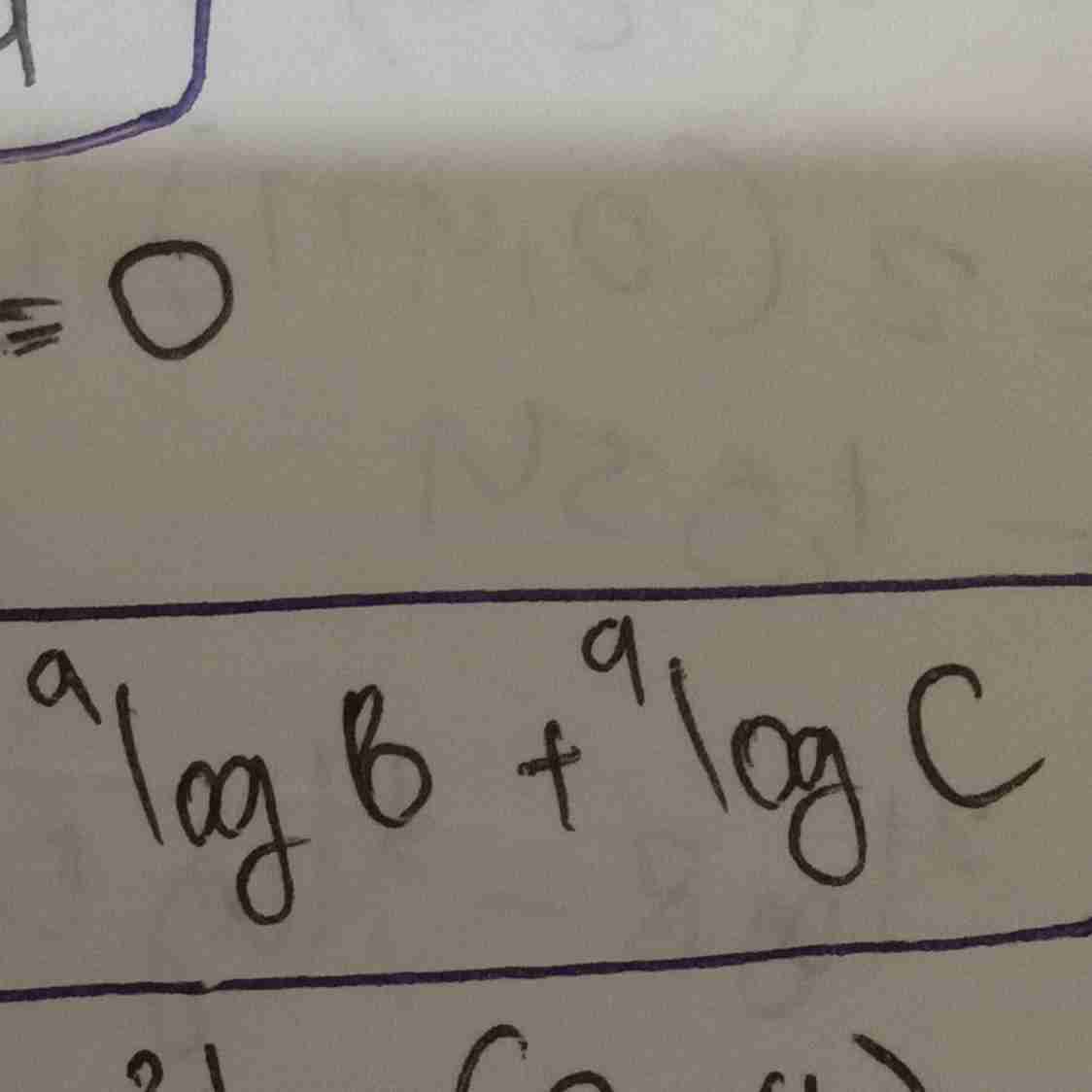
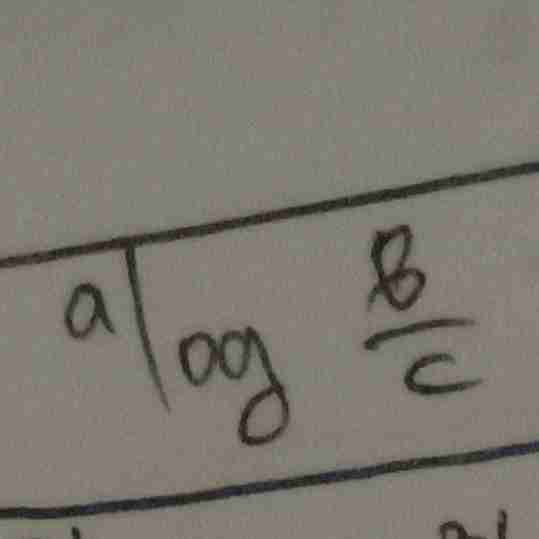
logaritma

dikurang

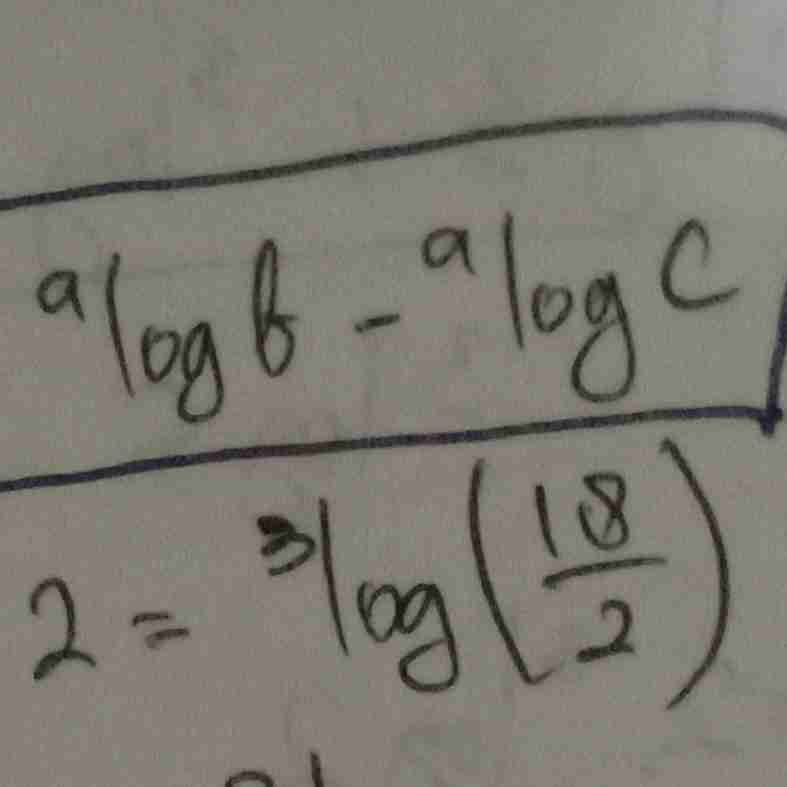
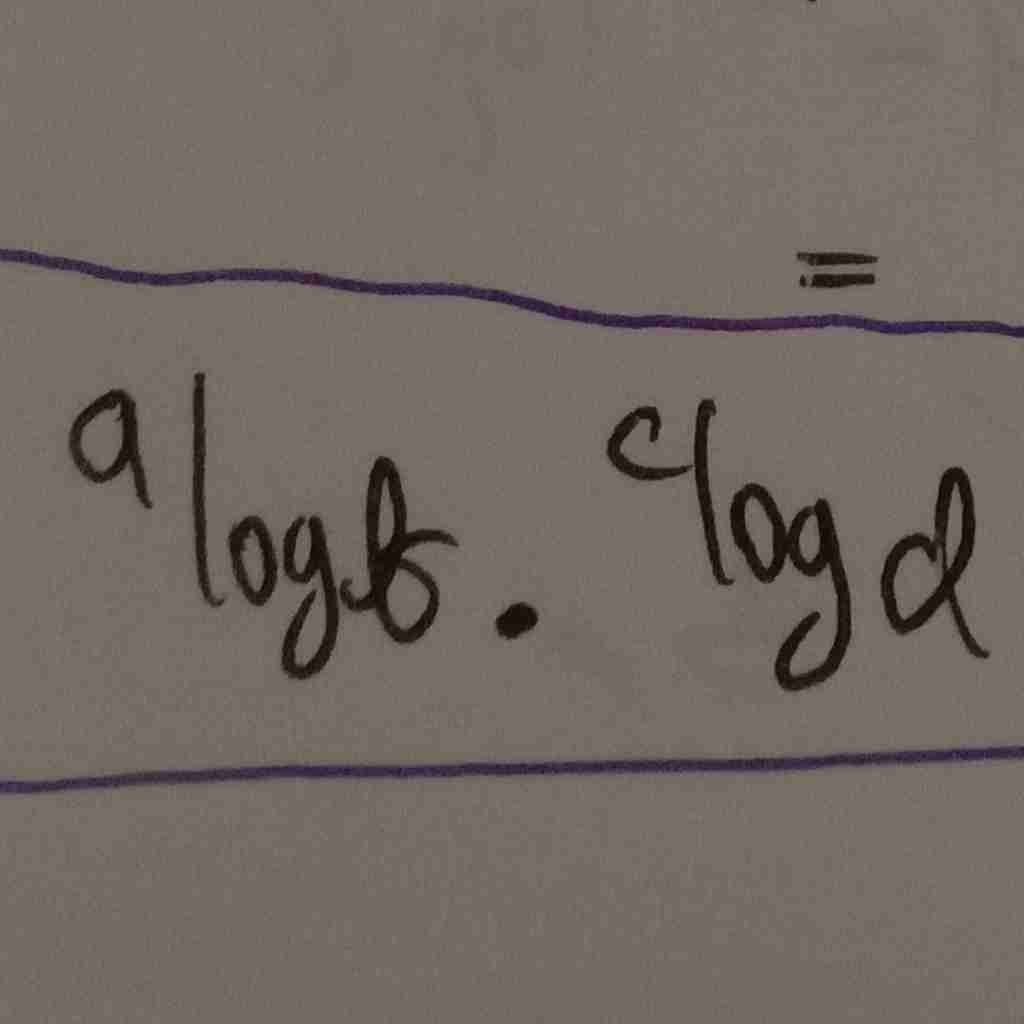
logaritma

basis nya bisa di tukar

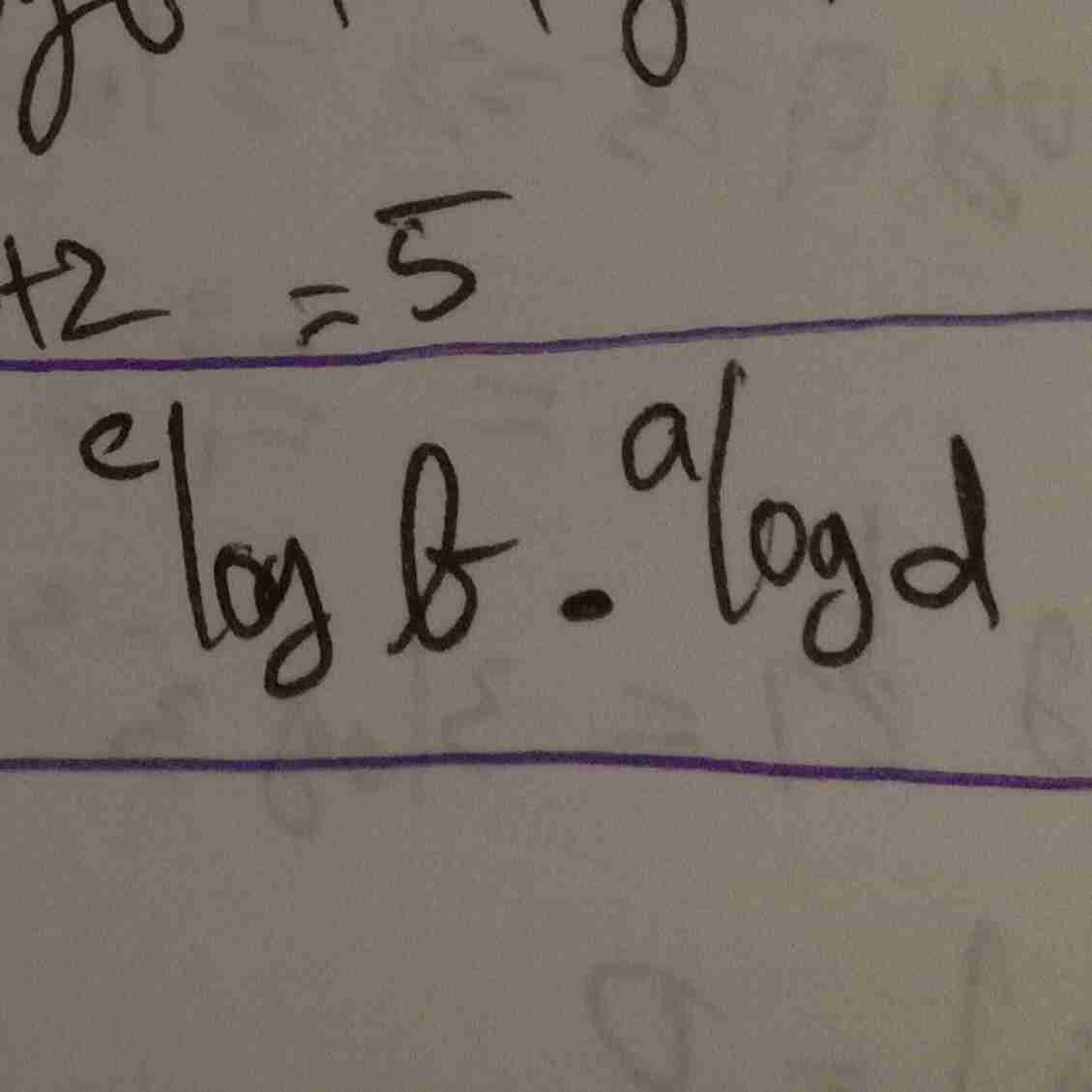
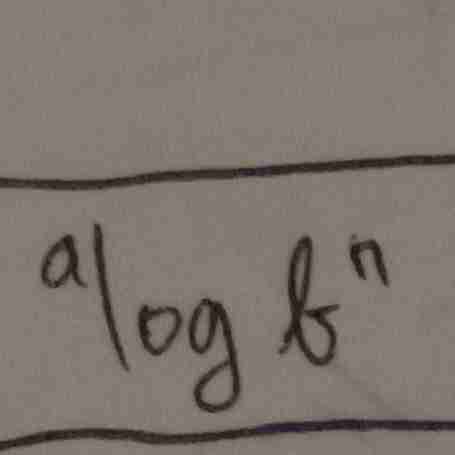
logaritma

pangkat numerus di keluarkan

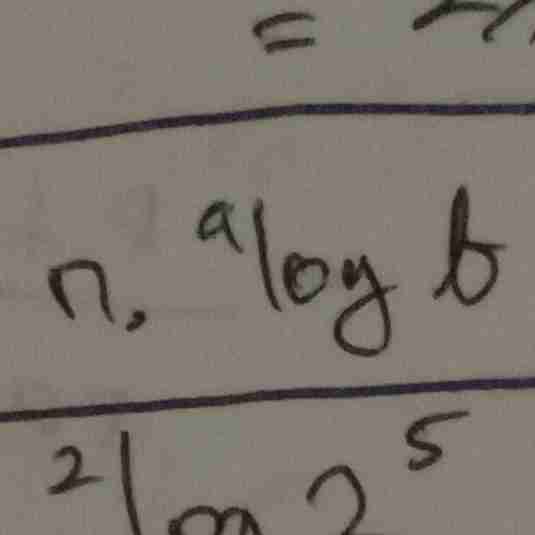
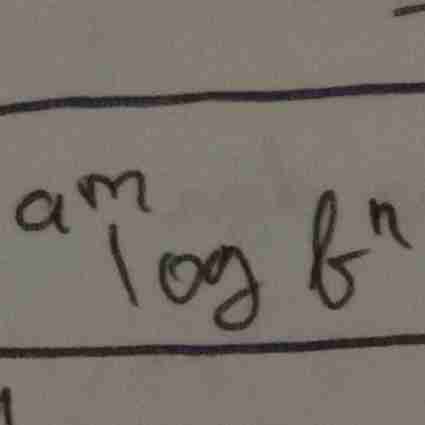
logaritma

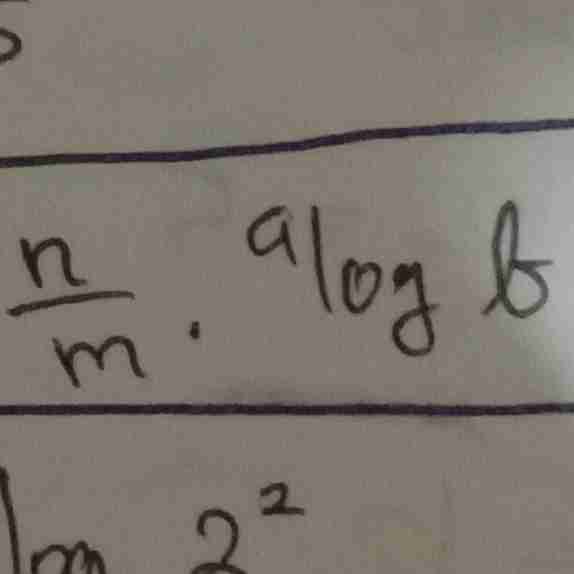
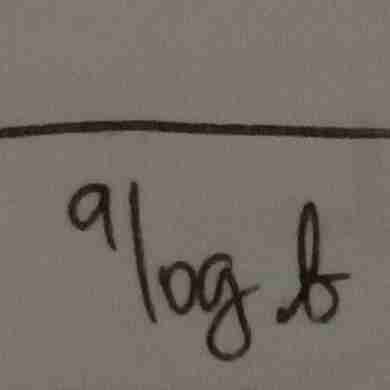
sifat logaritma

tukarkan a dan b menjadi?

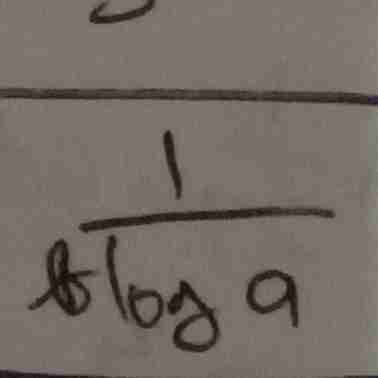
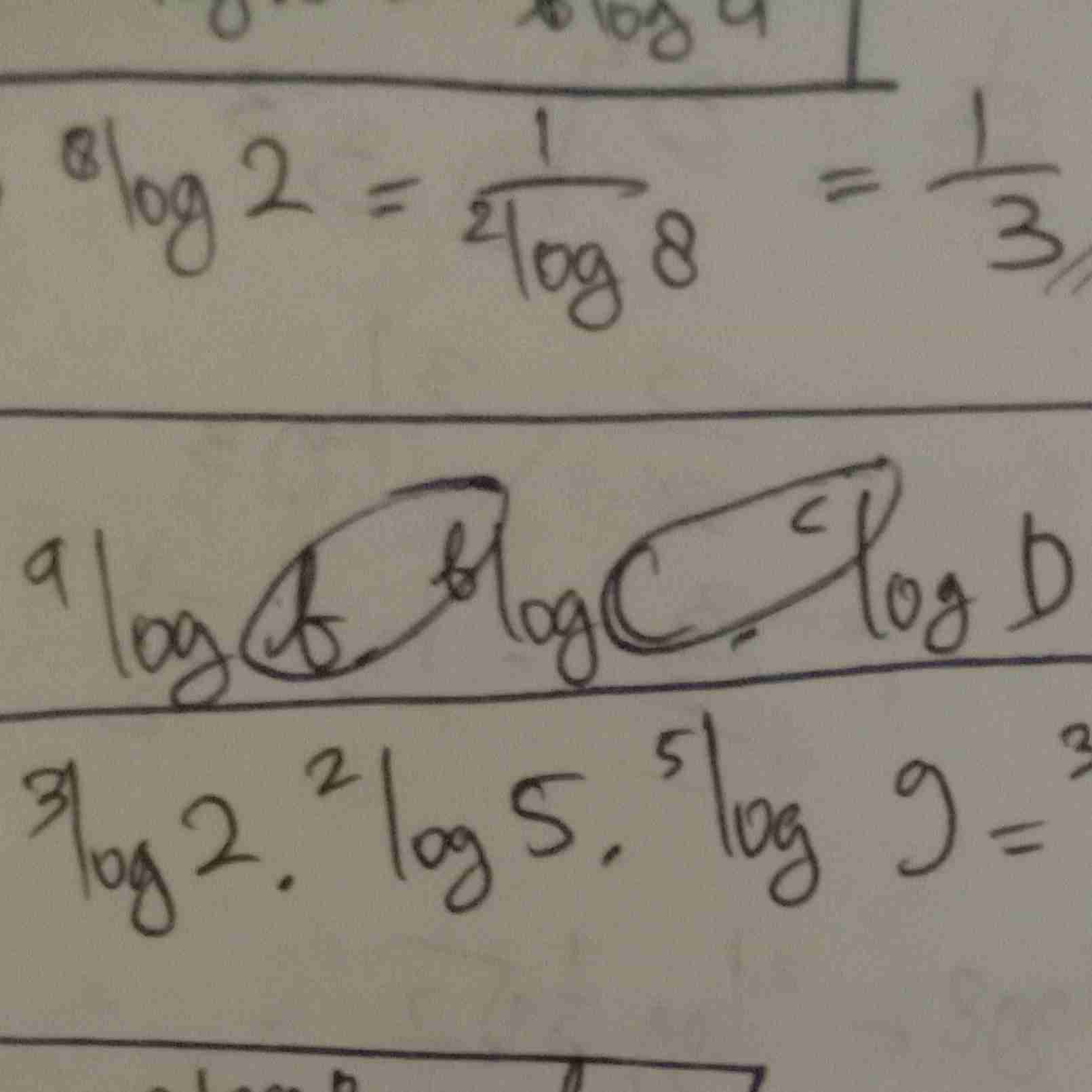
sifat logaritma

sederhanakan bentuk ini

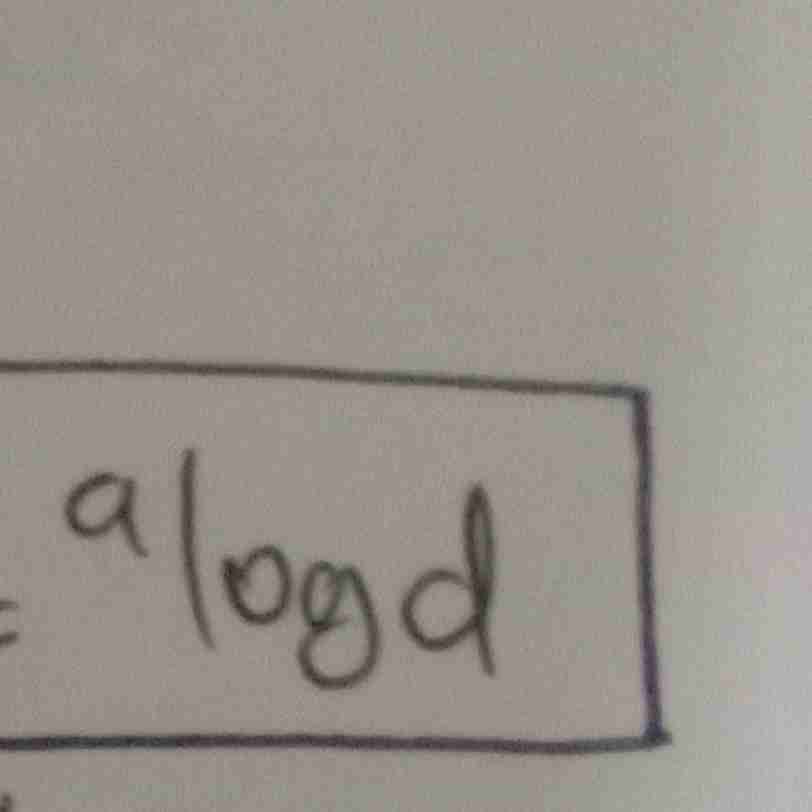
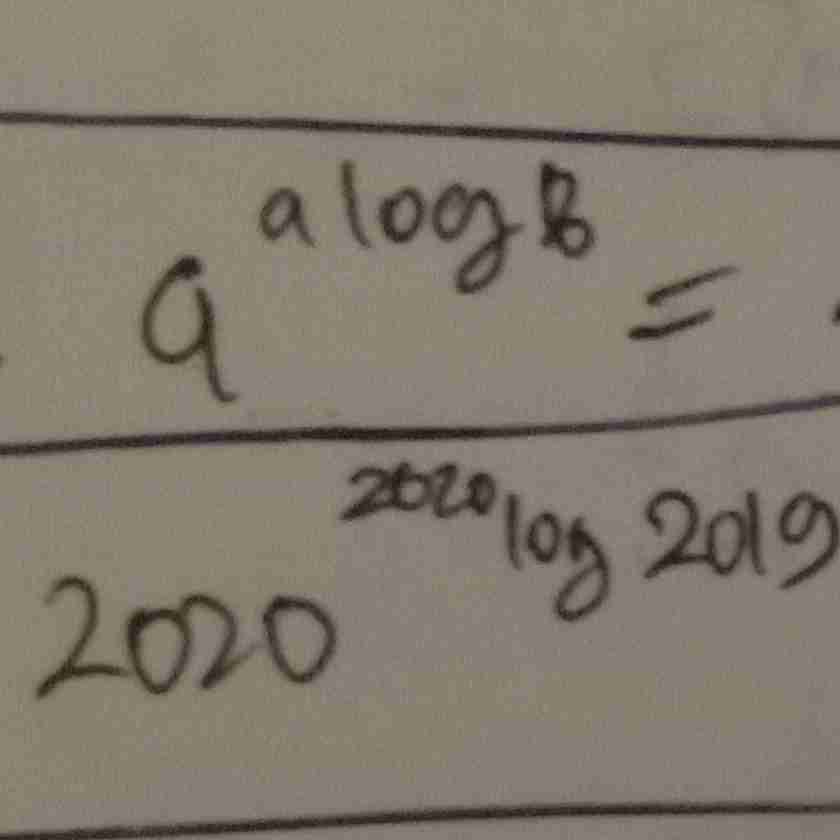
sifat logaritma

bisa disederhanakan menjadi?

numerus pada pangkat a

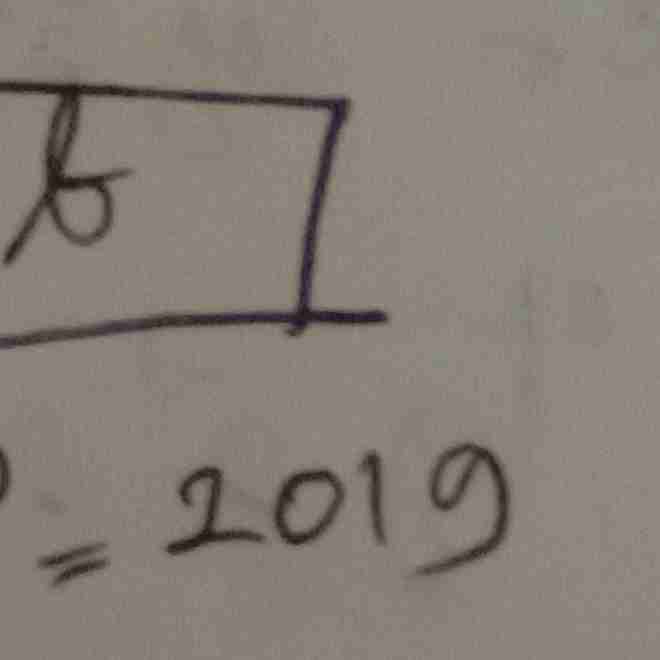
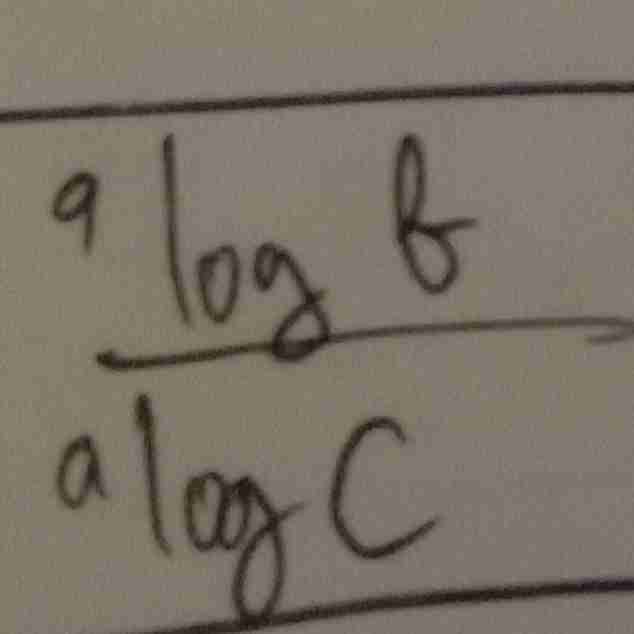
sifat logaritma

bisa disederhanakan menjadi?

numerus pada penyebut bisa menjadi basis

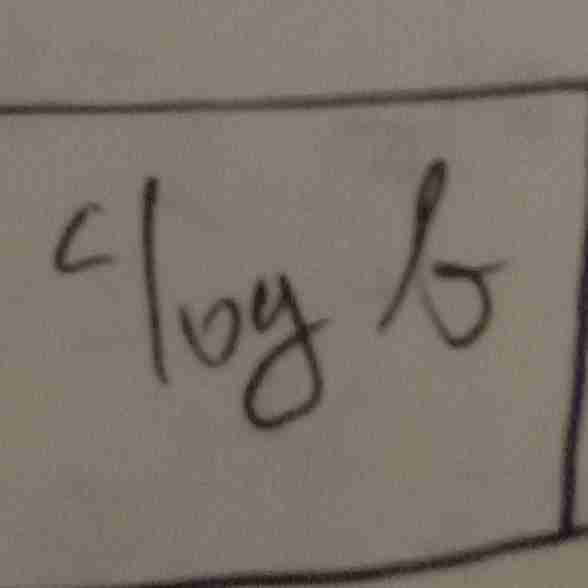
Trigonometri

mencari sin x = ?

depan/miring

Trigonometri

mencari cos x ?

samping/miring

Trigonometri

mencari tan x =?

depan/samping

Persamaan kuadrat

Rumus abc mencari X1,2

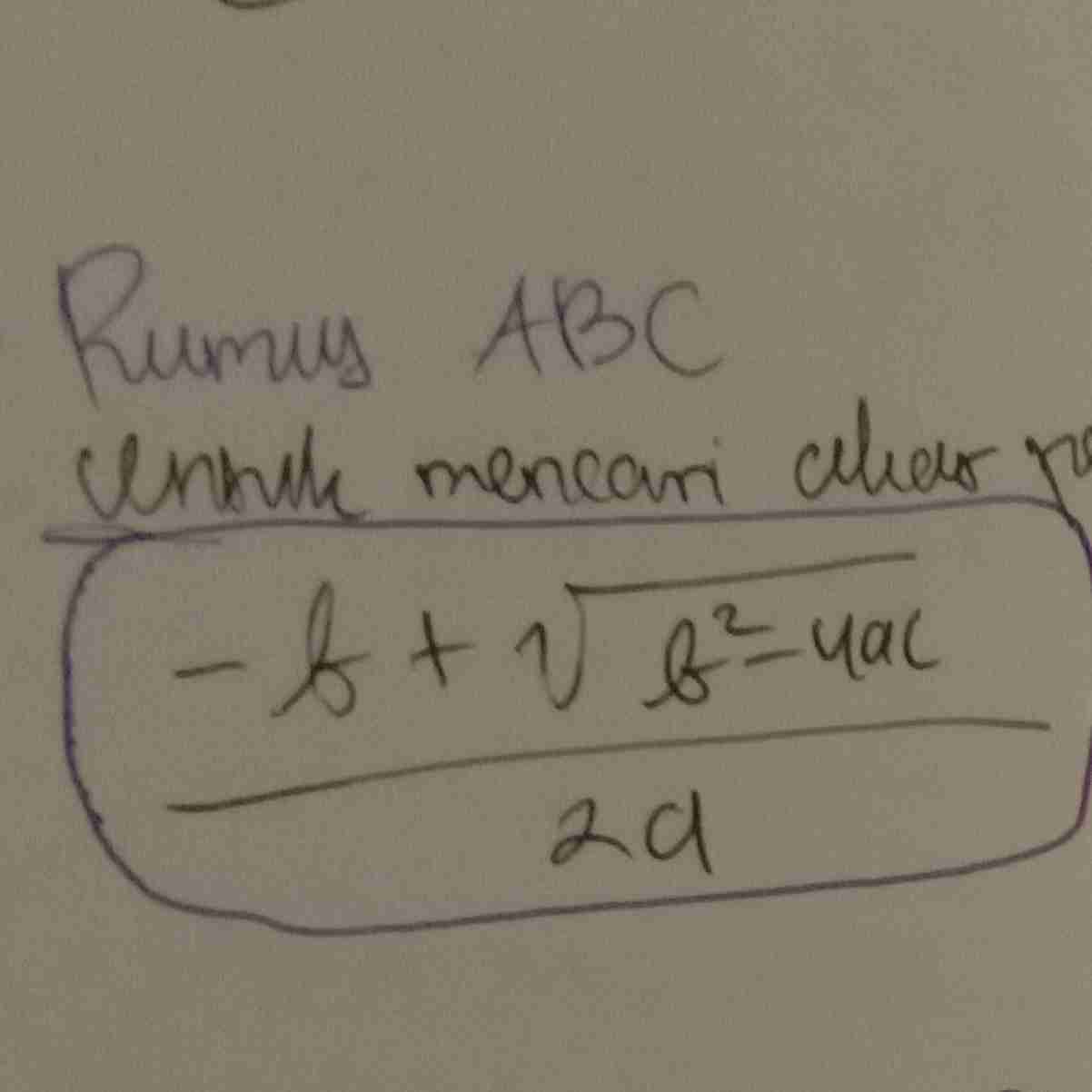
Bentuk Umum fungsi kuadrat adalah

ax²+bx+c

Titik puncak adalah

titik max/min sebuah kurva fungsi kuadrat (Xp,Yp)

rumus mencari Xp adalah

•-b/2a

• ½ (-b/a) = ½(X1+X2)

rumus mencari Yp adalah

• masukan Xp (jika Xp telah diketahui) ke persamaan fungsi => f(xp)

• D/-4a = b²-4ac/-4a

jika a>0 maka titik puncak bernilai?

Nilai/titik minimum

jika a<0 maka titik puncak bernilai?

Nilai/titik maksimum

Nilai maksimum/minimum sama dengan?

Yp (Y puncak)

Sumbu simetri kurva fungsi kuadrat merupakan?

X = Xp (X puncak)

Jika Titik potong di sumbu x maka nilai Y?

Y = 0

Jika Titik potong di sumbu y maka Nilai X ?

•X = 0

•Y = C

sederhanakan

f(x) = 2x²+x-1/3x+3

•(2x-1)(x+1)/3(x+1)

• 2x-1/3

Rumus abc untuk mencari akar persamaan kuadrat

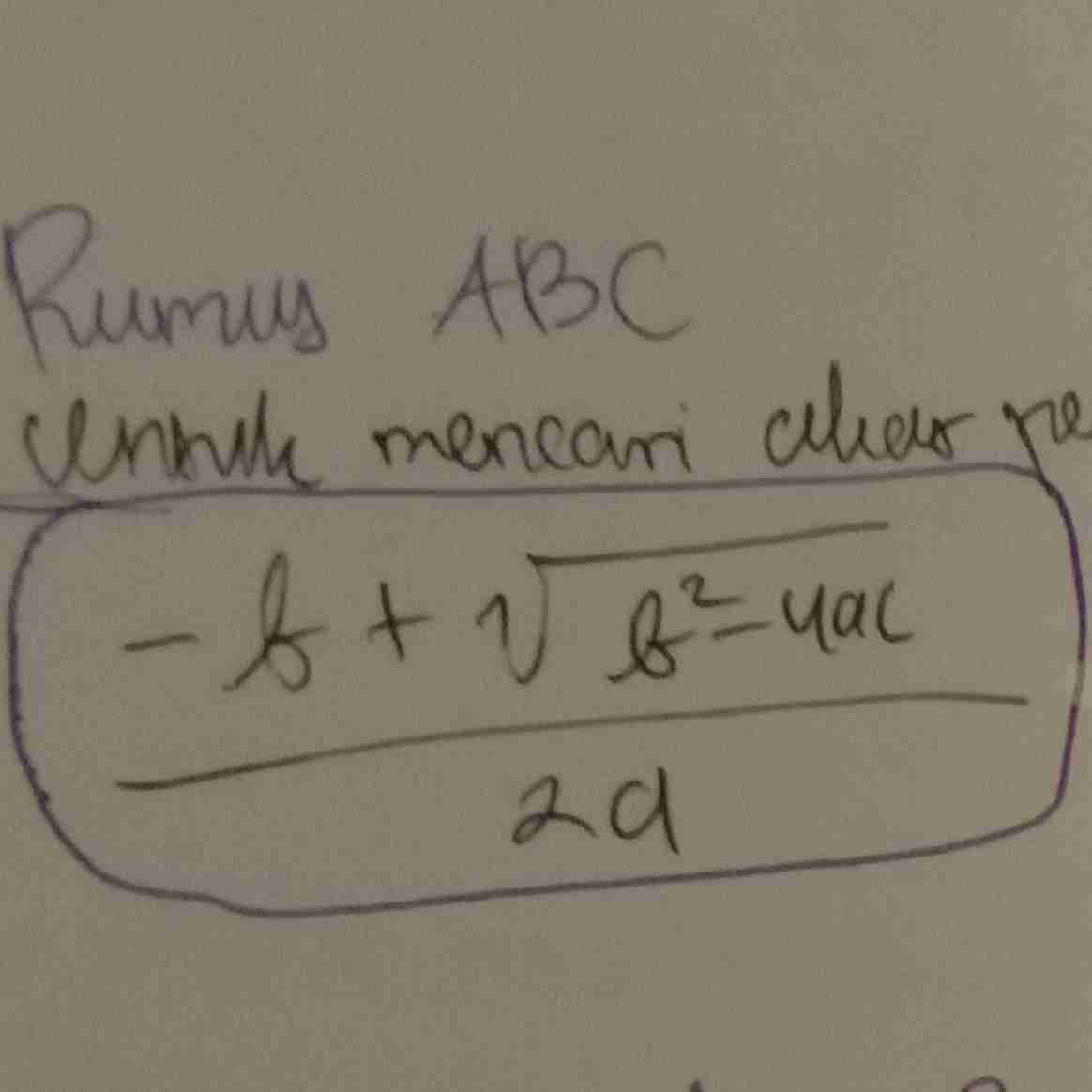
Rumus mencari akr pers kuadrat

X1-X2 ?

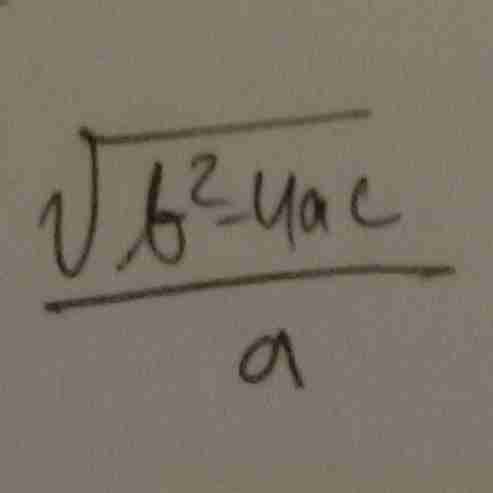
X1² - X2² ? bentuk lainnya….

(X1+X2)(X1-X2)

jika akar” berlain tanda, maka nilai x1 dan x2 dikalikan bernilai?

X1×X2 < 0

bentuk lainnya dari …

a²+b²

(a+b)² - 2ab

rumus gradien(kemiringan) dari persamaan ax²+bx+c adalah

m = -a/b

rumus gradien jika diketahui titik yang dilalui

•m= Y-Y1/X-X1

•(y-y1)=m(x-x1)

jika garis 1 dan garis 2 sejajar maka kemiringan garis keduanya?

m1=m2

jika garis 1 tegak lurus garis 2 maka nilai kemiringan garis nya?

m1×m2 = -1

a<0

sifat kurva ?

kurva terbuka keatas

bernilai minimum

a>0

sifat kurva ?

kurva terbuka kebawah

bernilai maximum

kofisien b bernilai 0 (nol) jika kurva?

kurva ditengah sumbu Y

koefisien a dan b bertanda sama (=) maka kurva terletak di ?

kurva terletak di kiri sumbu Y

koefisien a dan b berlain bertanda maka kurva terletak di ?

kurva terletak di kanan sumbu Y

koefisien c > 0 jika kurva ?

kurva memotong sumbu y positif

koefisien c < 0 jika kurva ?

kurva memotong sumbu y negatif

rumus diskriminan (d) adalah?

b2-4ac

D > 0 maka kurva …..

kurva memotong garis x di 2 titik berbeda

D = 0 maka kurva …..

kurva menyinggung garis x

(X1=X2)

D < 0 maka kurva …..

kurva tidak memotong garis x

(Definit)

apa itu definit positif ?

nilai f(x) selalu positif

• a>0

• d<0

apa itu definit negatif?

nilai f(x) selalu negatif

• a<0

• d<0

nama lain garis tegak lurus adalah…

garis normal

cara menentukan persamaan Gradien pada grafik fungsi kuadrat (f(x)) adalah….

Gradien(M) = f’ (x)

• fungsi diturunkan

nilai Gradien(M) jika bentuk garis seperti ini : [/] ?

M>0

nilai Gradien(M) jika garis berbentuk seperti ini : [\] ?

M<0

matriks singular adalah

matriks yang tidak punya invers

• Determinan = 0

Rumus menentukan persamaan fungsi kuadrat jika di ketahui kedua titik puncak (Xp,Yp)

Y= a(X-Xp)²+Yp

Rumus Menentukan persamaan fungsi kuadrat jika diketahui memotong sumbu X di 2 titik berbeda:

(X1,0) dan (X2,0)

Y = a(X-X1)(X-X2)

Irisan A dan b

AnB

Gabungan A dan B

A U B

Transpose Matrik adalah

Mengubah Baris menjadi kolom

lambang determinan A

|A|

a b

c d

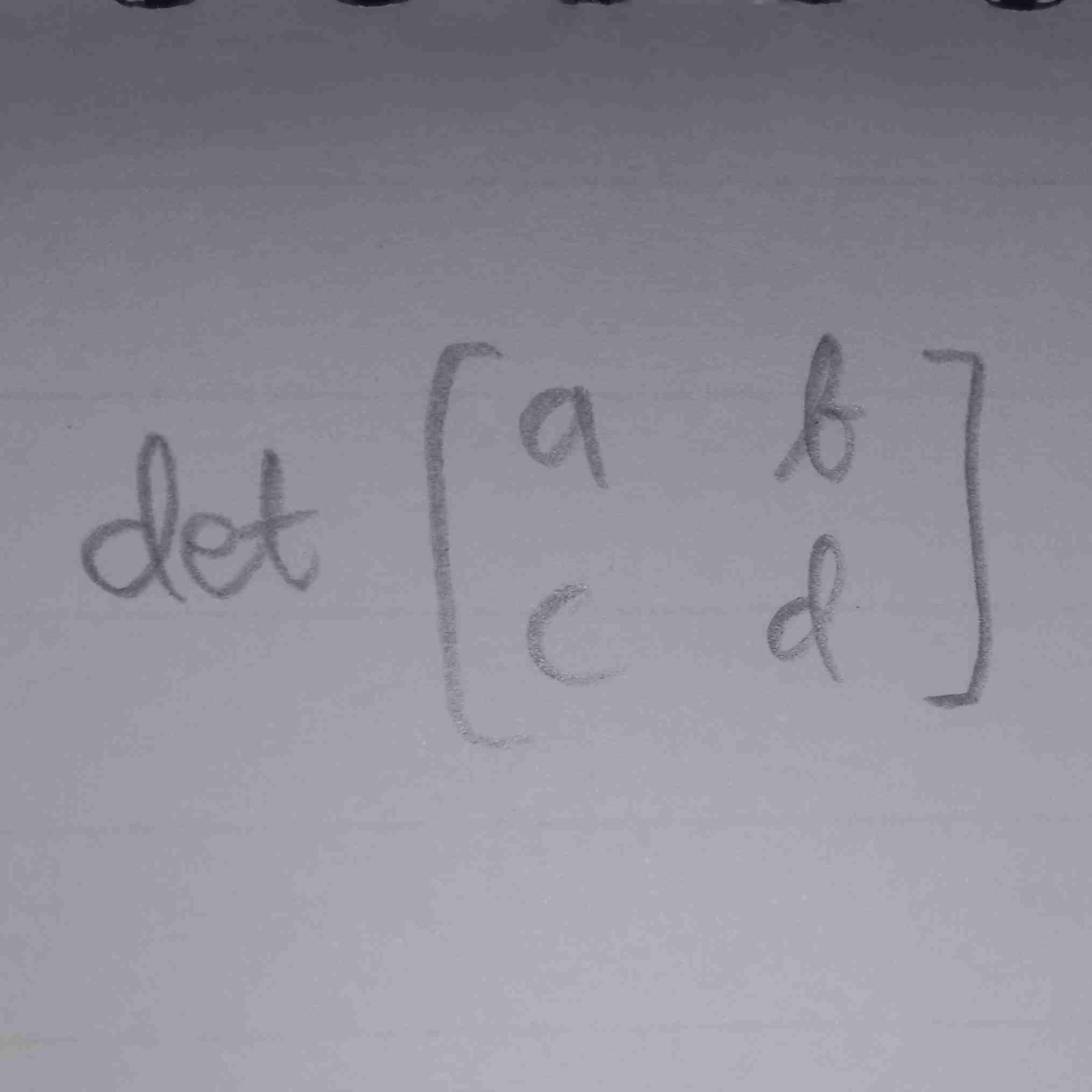
rumus determinan

(a.d) - (b.c)

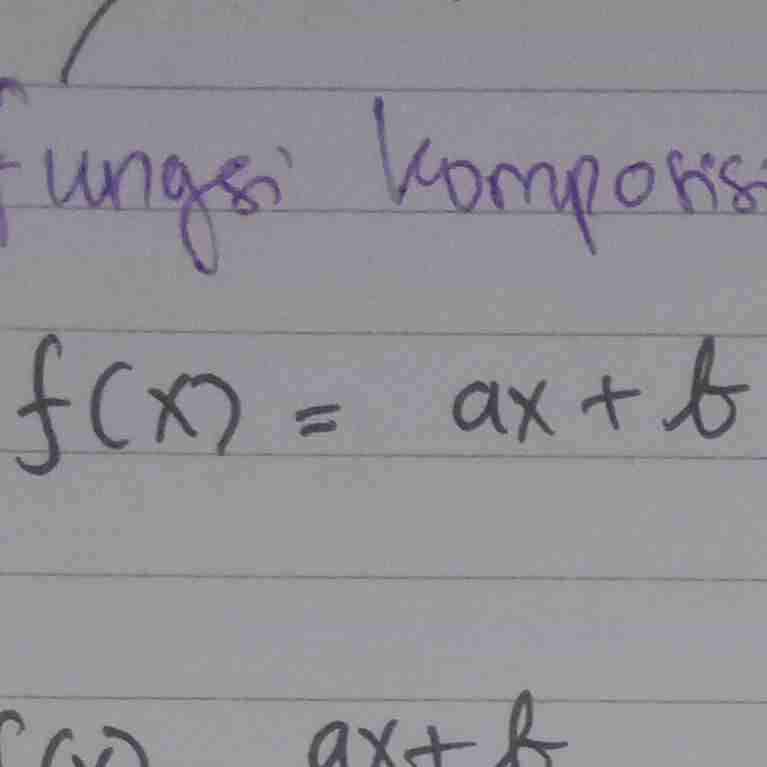
rumus invers nya

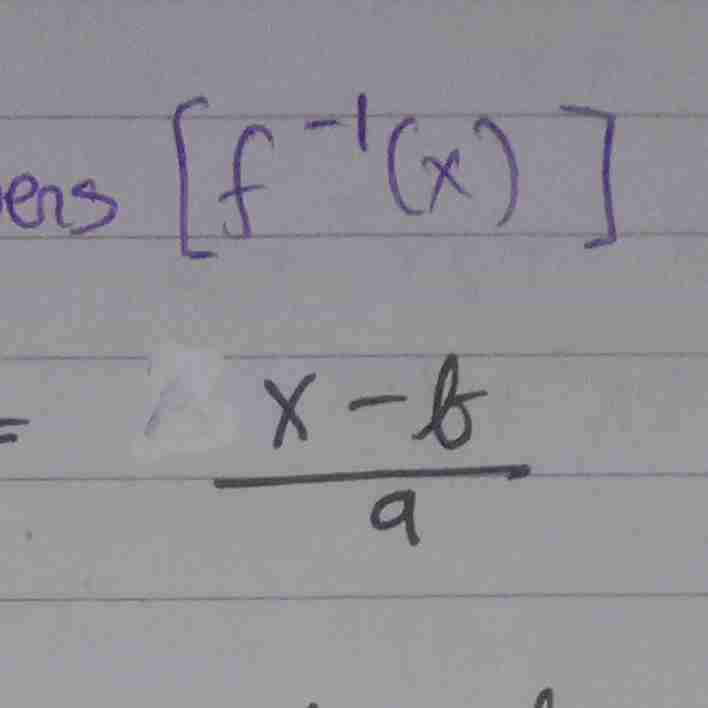
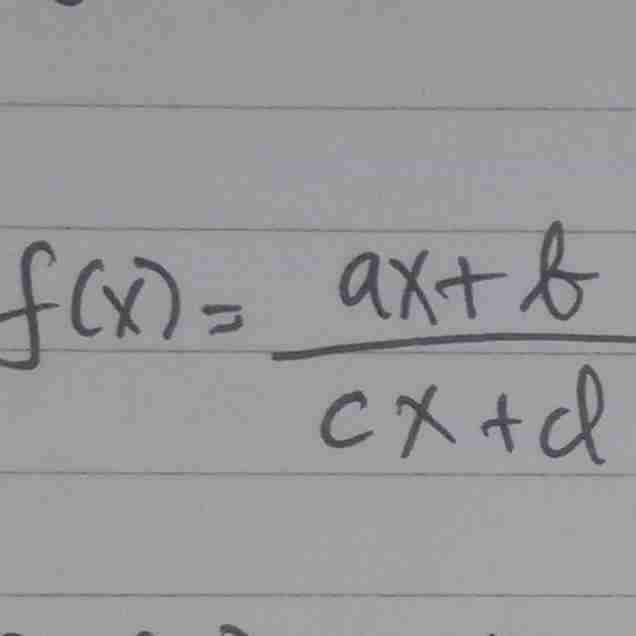
rumus inversnya

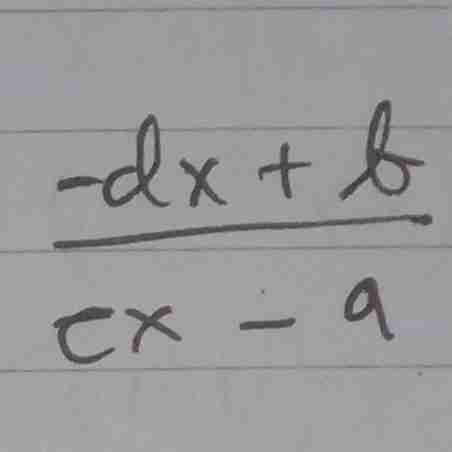
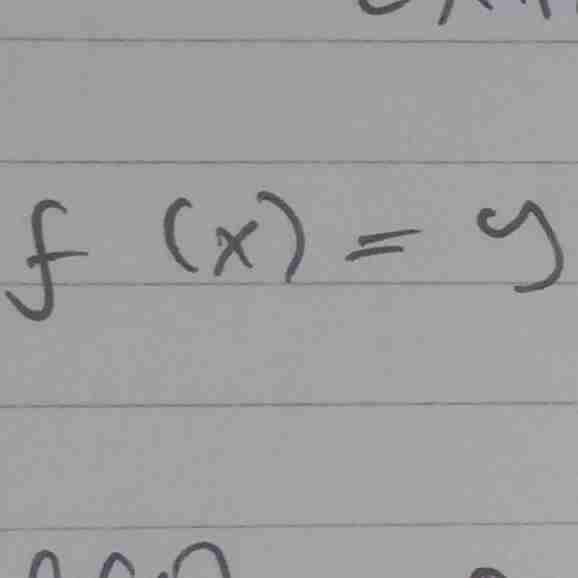
bentuk inversnya

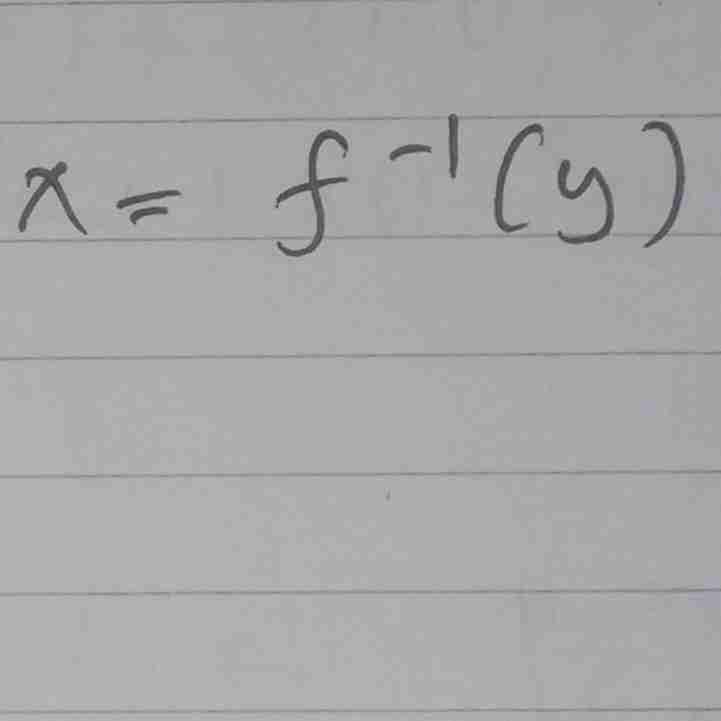
nama lain Fungsi adalah

Pemetaan

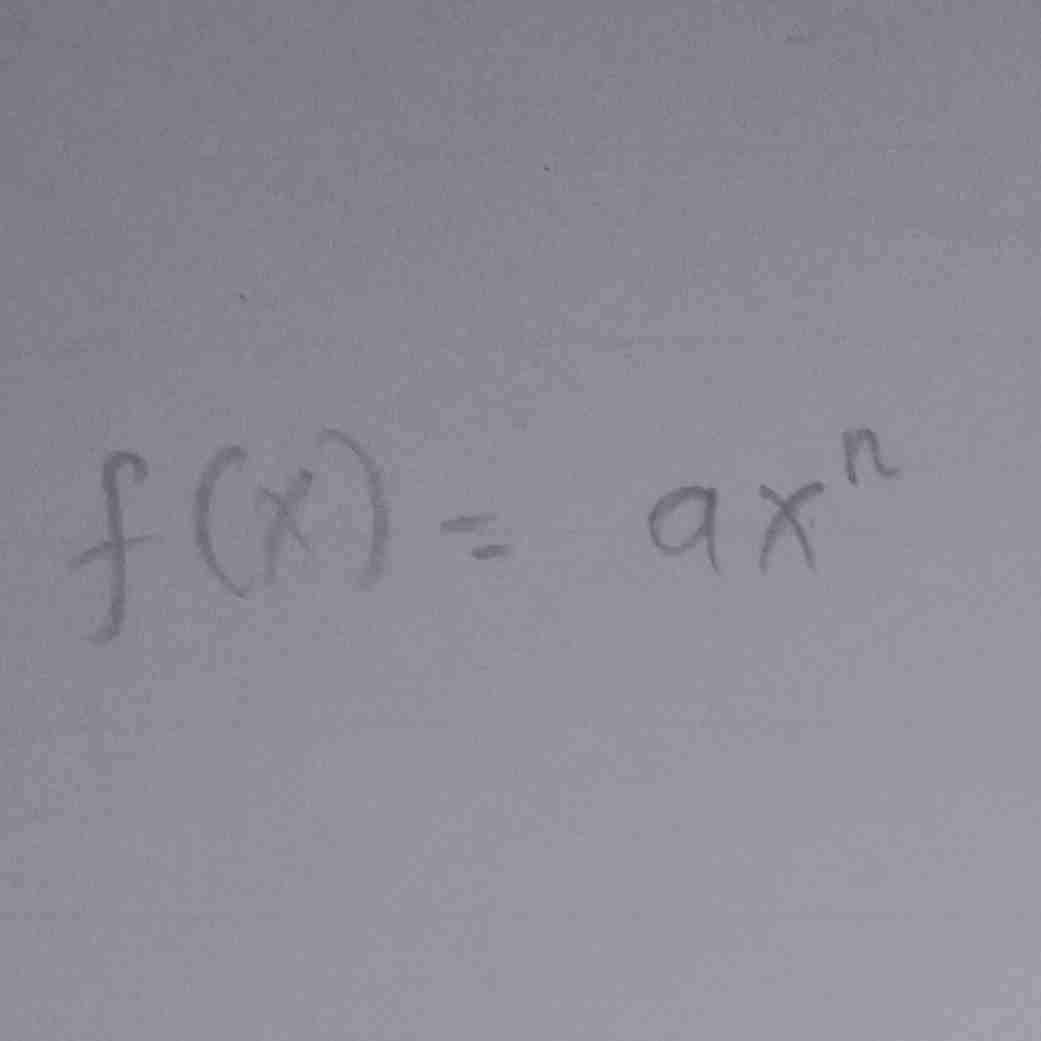
rumus turunannya

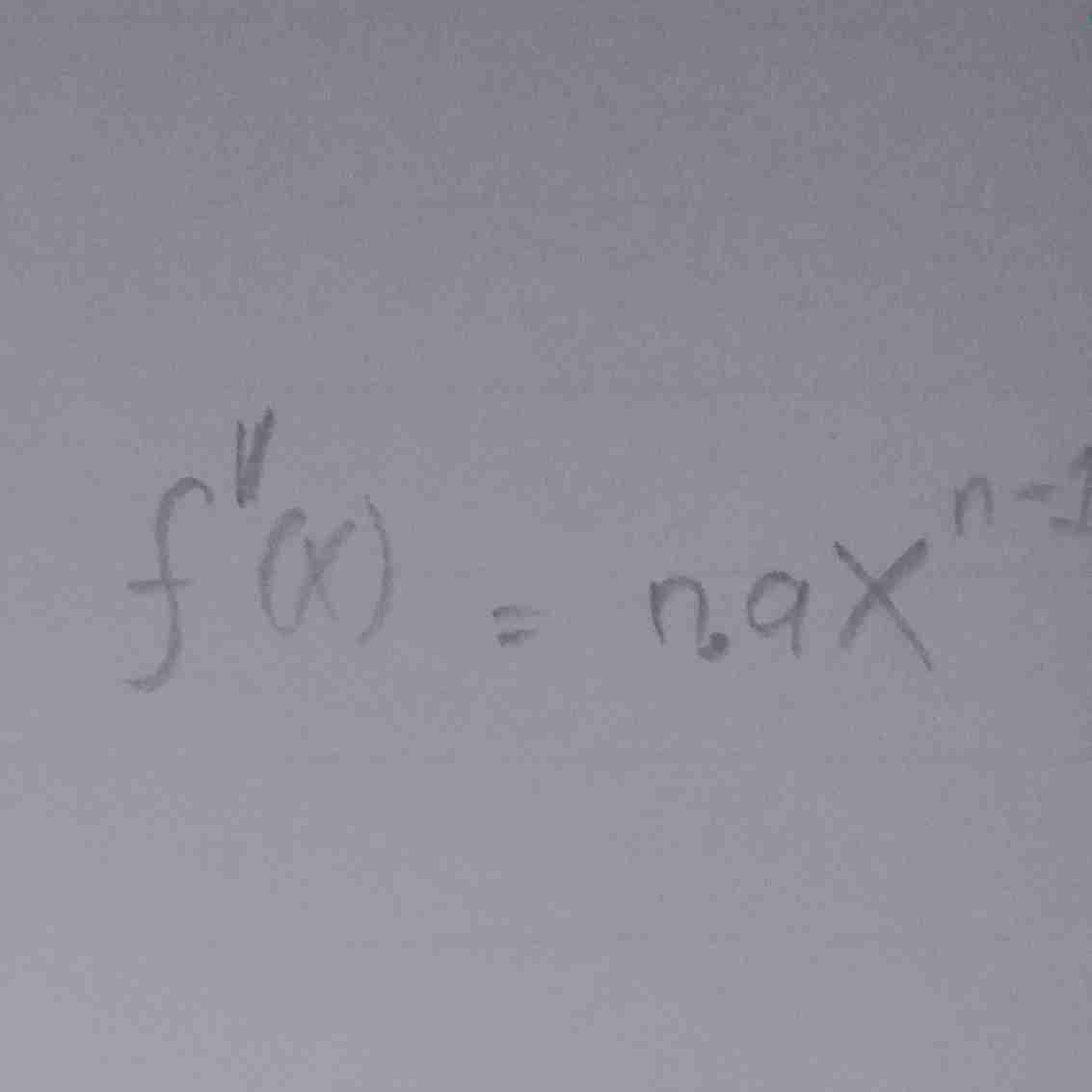
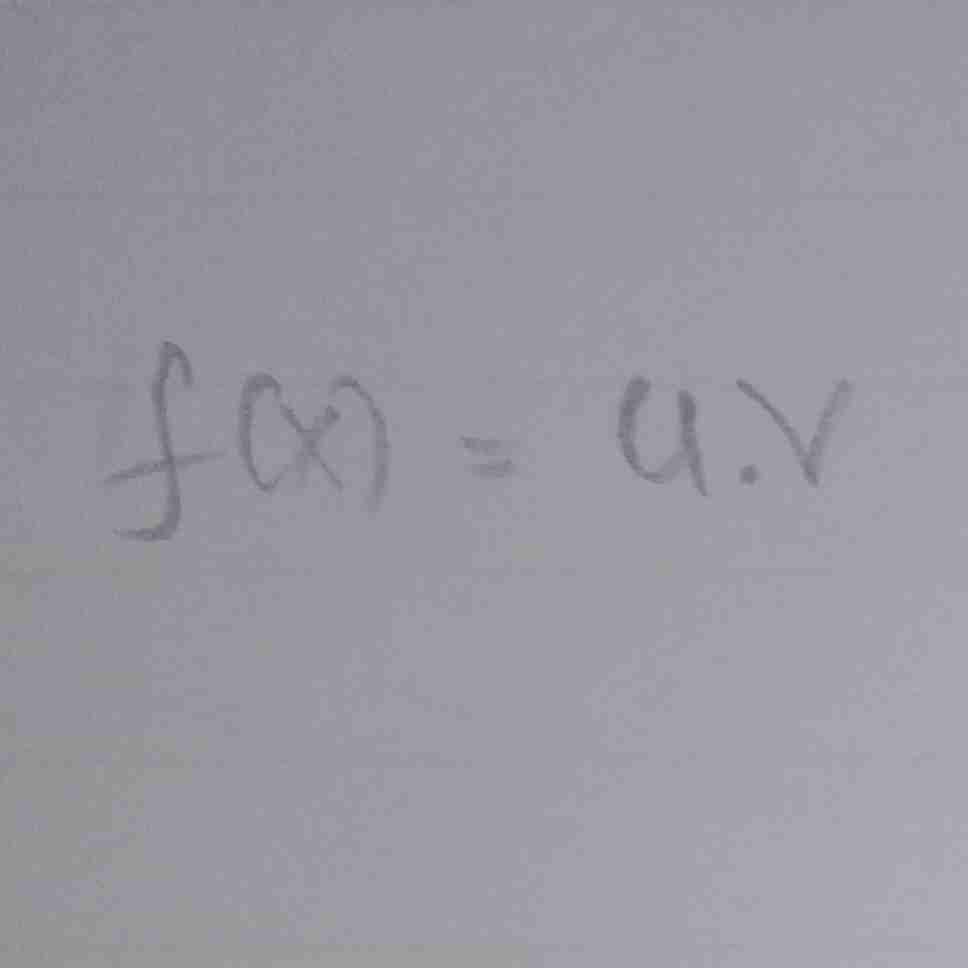
rumus turunannya…

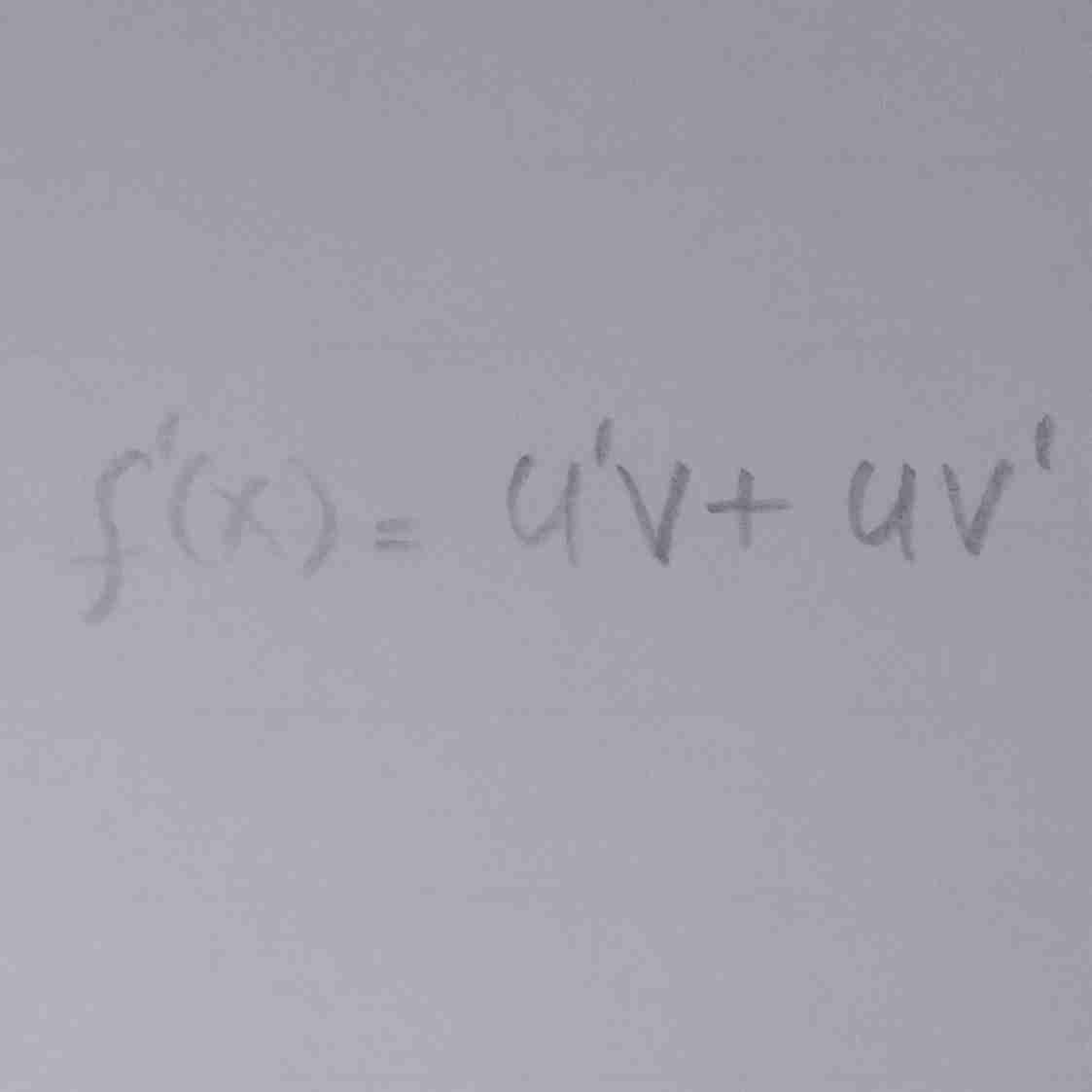
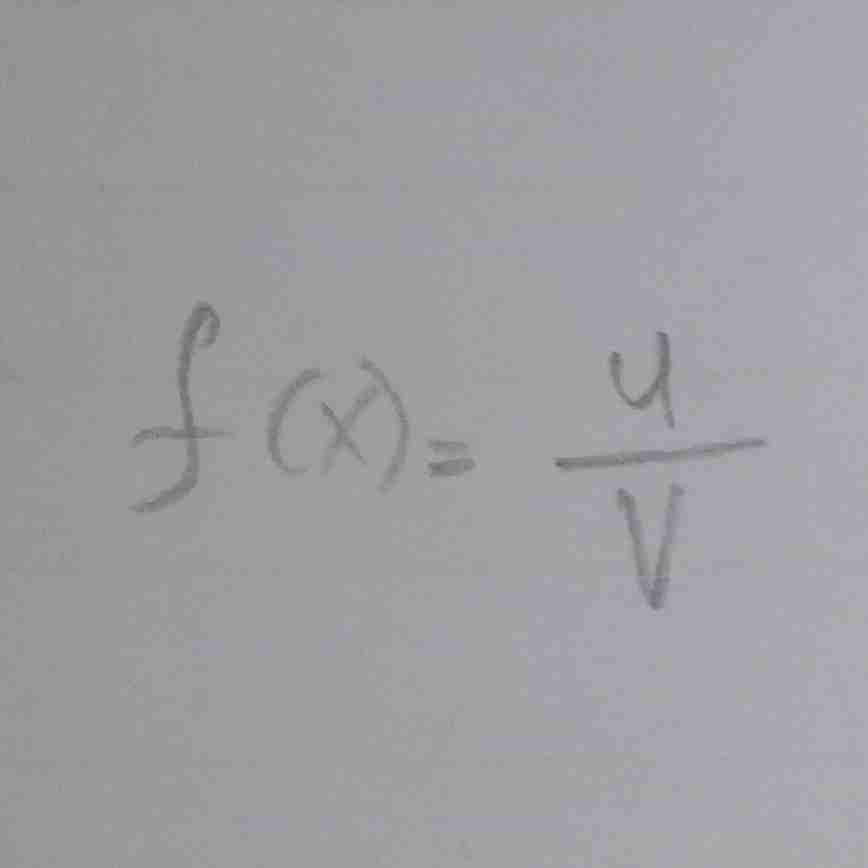
rumus turunannya….

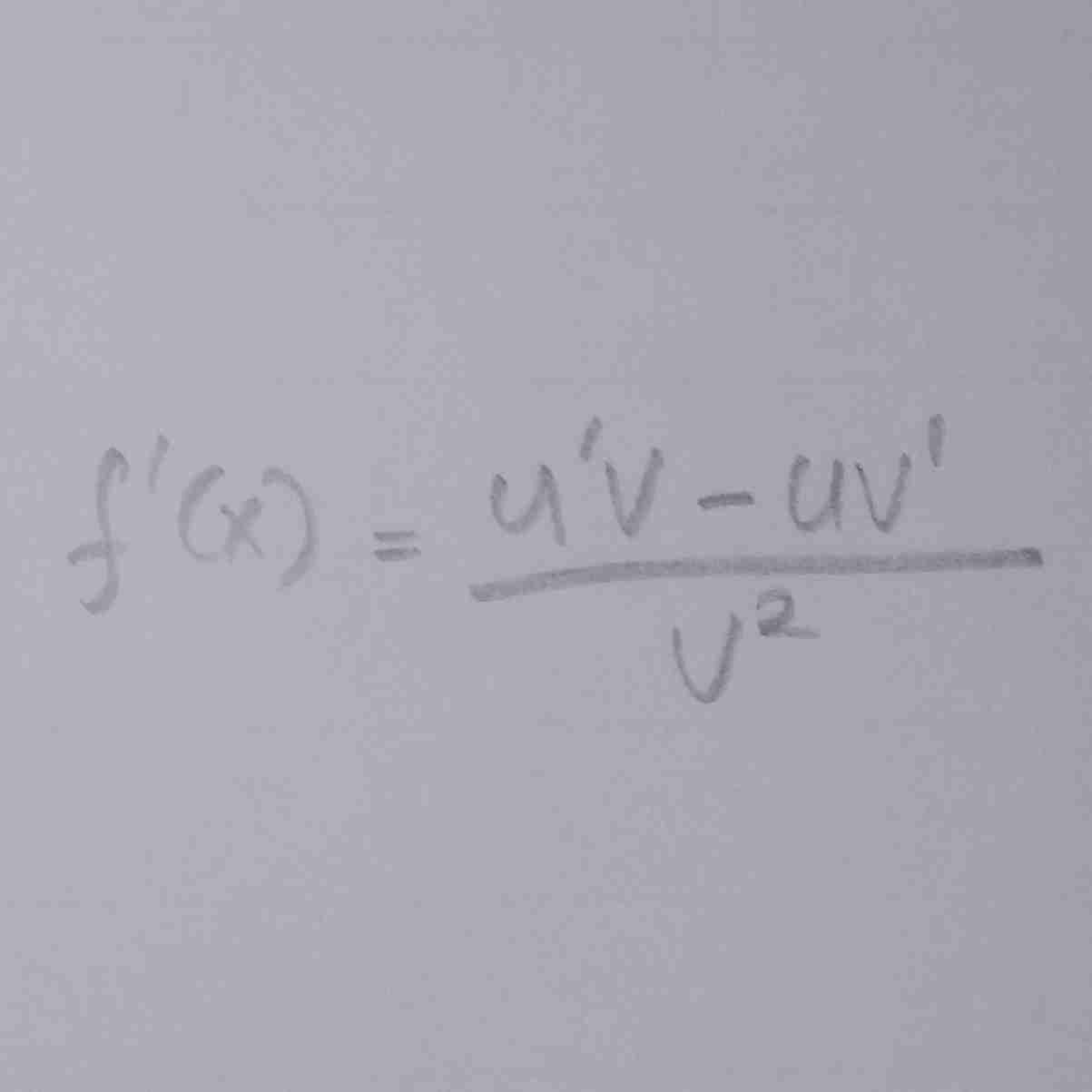
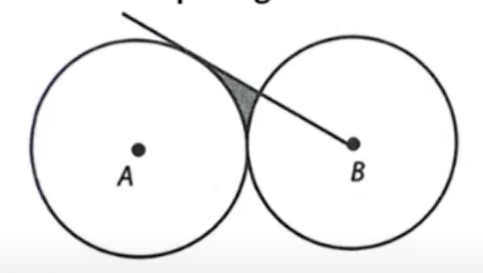
untuk menentukan panjang pusat A ke garis singgungnya adalah …

sepanjang jari-jari lingkaran A

jari-jari selalu tegak lurus dengan garis singgung sehingga membuat sudut siku-siku