Circles

perpendicular chords theorem thing? idk the name

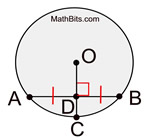
In a circle, a radius perpendicular to a chord bisects the chord.

Converse:  In a circle, a radius that bisects a chord is perpendicular to the chord.

Also stated:  In a circle, the perpendicular bisector of a chord passes through the center of the circle

Extended form: In a circle, a diameter perpendicular to a chord bisects the chord and its arc.

Chords equidistant theorem thingy? (just look at the back of the flashcards for the theorems idk wtf to put on the front)

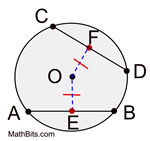
In a circle, or congruent circles, congruent chords are equidistant from the center.

Converse:  In a circle, or congruent circles, chords equidistant from the center are congruent.

Arcs and congruent chords theorem

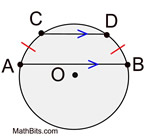
In a circle, parallel chords intercept congruent arcs

What are common tangents?

What are internal tangents?

What are external tangents?

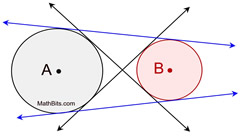
Common tangents are lines, rays or segments that are tangent \\n to more than one circle at the same time.

A common internal tangent of two circles is a tangent of both circles that intersects the segment joining the centers of two circles.

External tangents are lines that do not cross the segment joining the centers of the circles.

In the picture there are: 4 Common Tangent, 2 external tangents (blue),2 internal tangents (black)

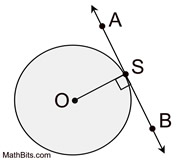
tangents and radius theorem

If a line is tangent to a circle, it is perpendicular to the radius drawn to the point of tangency.

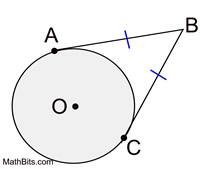
tangent lines to circles theorem

Tangent segments to a circle from the same external point are congruent.

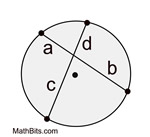
If two chords intersect in a circle, the product of the lengths of the segments of one chord equal the product of the segments of the other.

Formula: *a • b = c • d*

What is a secant?

A straight line that intersects a circle in two points.

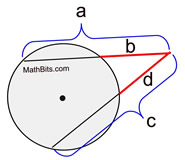
If two secant segments are drawn to a circle from the same external point, the product of the length of one secant segment and its external part is equal to the product of the length of the other secant segment and its external part.

Formula: *a • b = c • d*

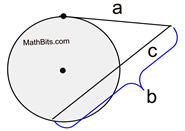
If a secant segment and tangent segment are drawn to a circle from the same external point, the length of the tangent segment is the geometric mean between the length of the secant segment and the length of the external part of the secant segment.

Formula: b/a=a/c or b•c

=a^2

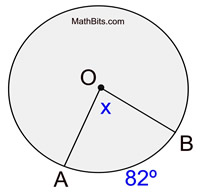
Central Angle = Intercepted Arc

What is a central angle?

A central angle is an angle formed by two radii with the vertex at the center of the circle.

what is an inscribed Angle?

An inscribed angle is an angle with its vertex "on" the circle, formed by two intersecting chords.

\

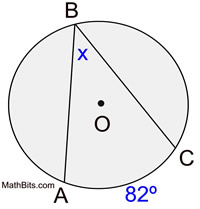
Inscribed Angle =1/2 Intercepted Arc

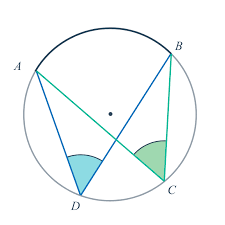
Theorem

In a circle, inscribed angles that intercept the same arc are congruent.

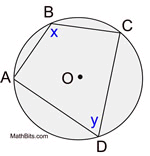
The opposite angles in a cyclic quadrilateral are supplementary.

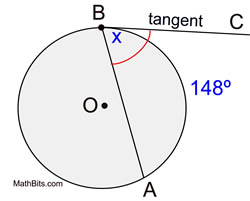
theorem

An angle formed by an intersecting tangent and chord has its vertex "on" the circle.

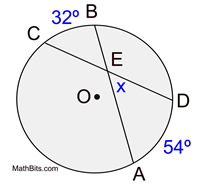
When two chords intersect inside a circle, four angles are formed. At the point of intersection, two sets of congruent vertical angles are formed in the corners of the X that appears.

Area of a circle

A=πr^2

circumference of a circle

C=2πr

Area of a sector

θ/360πr^2

θ= central angle

Length of an arc

θ/360 2πr

θ= central angle

area of a segment

area of the sector - the triangle (use trigonometry)