GCSE Circle Theorems

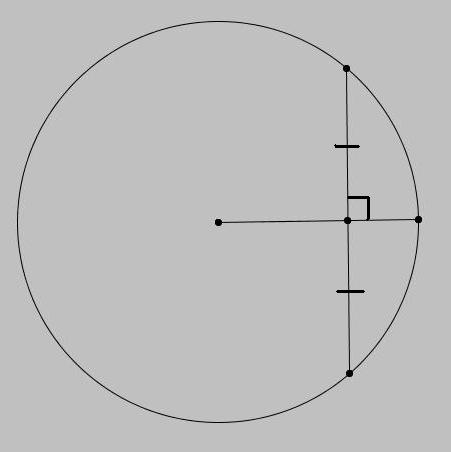
Perpendicular bisector of chord passes through centre.

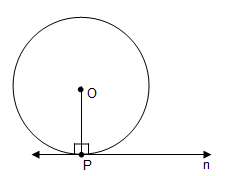
Angle between tangent and radius is 90o.

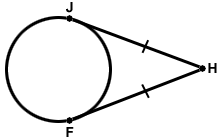
Tangents from same point are equal in length.

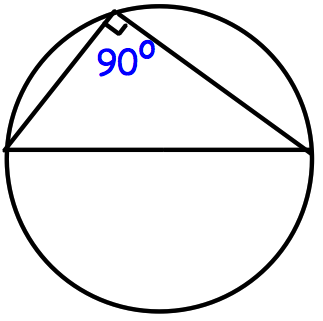
Angle in semi-circle is 90o.

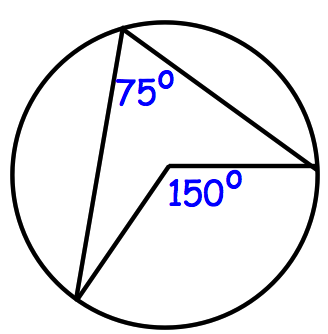
Angle at centre is twice angle at circumference.

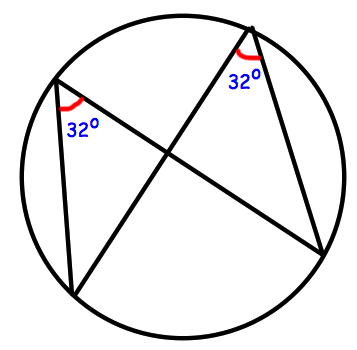
Angles in same segment are equal.

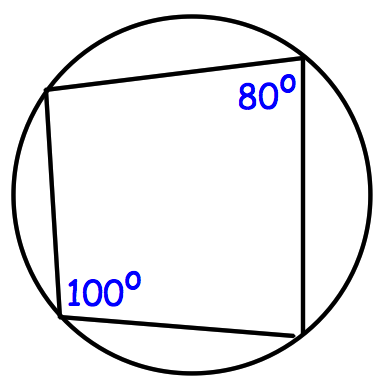
Opposite angles of cyclic quad add up to 180o.

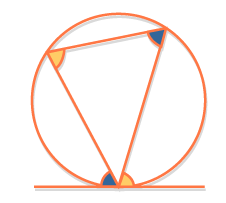
Alternate Segment Theorem

Same segment theorem

Angles in the same segment are equal

Angle at circumference and centre theorem

The angle at the centre is twice the angle at the circumference

Angles in semi circle theorem

The angle in a semi circle is a right angle

Cyclic quadrilateral theorem

Opposite angles of a cyclic quadrilateral add up to 180*

Tangents from a point theorem

Tangents from a point are equal

Tangents and radius theorem

A tangent meets the radius at a right angle

Bisecting tangent theorem

The line from a point to the centre of a circle bisects the angle between the tangents from a point

Radius and chord theorem

A radius bisects a chord at 90*

Alternate angles

Alternate angled are equal.

parts of a circle

sector - pizza slice
segment - wonky semi-circle
arc - crust
circumference - perimeter
chord - dodgy diameter
radius - to middle
diameter - side to side through middle
tangent - straight line outside circle

prove the circle theorem:
The angle at the centre is twice the angle at the circumference

w = 180 - 2x
z = 180 - 2y
w + z + a = 360
(180 - 2x) + (180 - 2y) + b = 360
360 - 2x - 2y + b = 360
2x - 2y + b = 0
b = 2x + 2y

angle at circumference = x + y
angle at centre = 2x + 2y

prove the circle theorem:
Angles in the same segment are equal

draw 2 radius. prove using circle theorem 1 (angle at the centre is twice the angle at the circumference)

prove the circle theorem:
Angle in semi-circle is 90o.

using circle theorem 1 (angle at the circumference is twice the angle at the circumference)

angle at centre is 180 so half is 90

prove circle theorem:
tangents to a circle which meet at a point are equal in length

draw 2 radius to the tangent to create 2 semi-circles
then draw a line from the centre of circle to the point where the tangents meet.

this creates 2 congruent triangles according to ASS. (side in common, radius edge, 90 degree angle)

important point to note about angles in the same segment.

they must touch the circumference

prove the circle theorem:
angles in alternate segments are equal

draw a diameter that is 90 degrees to the tangent. Draw a triangle within the semi circle.

This means that angle in semi circle is 90 and the angle between the tangent and diameter in the alternate segment is also 90.

prove the circle theorem:
opposite angles in a cyclical quadrilateral total 180

draw 2 radii.

the 2 angles at the circumference are x and y.

then apply the rule (angle at the circumference is half the angle at the centre).

this means the angles at the centre are 2x and 2y.

2x + 2y = 360
x + y = 180

important note about alternate segment theory

all corners of triangle must be touching the circumference.

The centre of each circle is the origin

Find the equation of the tangent to the circle x^2 + y^2 = 169 at the point B (5, -12)

Find the equation of the tangent to the circle x^2 + y^2 = 225 at the point C (9,12)

Find the equation of the tangent to the circle x^2 + y^2 = 100 at the point D (-8,6)

Find the equation of the tangent to the circle x^2 + y^2 = 289 at the point E (-8,-15)

(use coordinates to find gradient of radius)

(gradient of tangent is the negative reciprocal as it is perpendicular)

substitute y and x in the straight line equation using the coordinates to find c

a circle has a centre (2,5) the point A (11,8)) lies on the circumference of the circle. Find the equation of the tangent to the circle at A.

y = 3x + 41