Math Basics (from Lecture 1)

what does SOH CAH TOA stand for?

SOH = sin, opposite, hypotenuse → sin() = length of opposite side / length of hypotenuse

CAH = cos, adjacent, hypotenuse

TOA = tan, opposite, adjacent

only applicable for right triangles

pythagorean theorem

a² + b² = c²

• where a and b are “straight sides” while c is the diagonal/hypotenuse

• only applies to right triangles

properties of equilateral/isoceles triangles

equilateral:

• all sides are the same length

• all interior angles are 60 degrees

isoceles:

• at least two sides are the same length

• at least two angles are the same

sin and cos addition laws

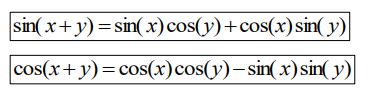
unit circle

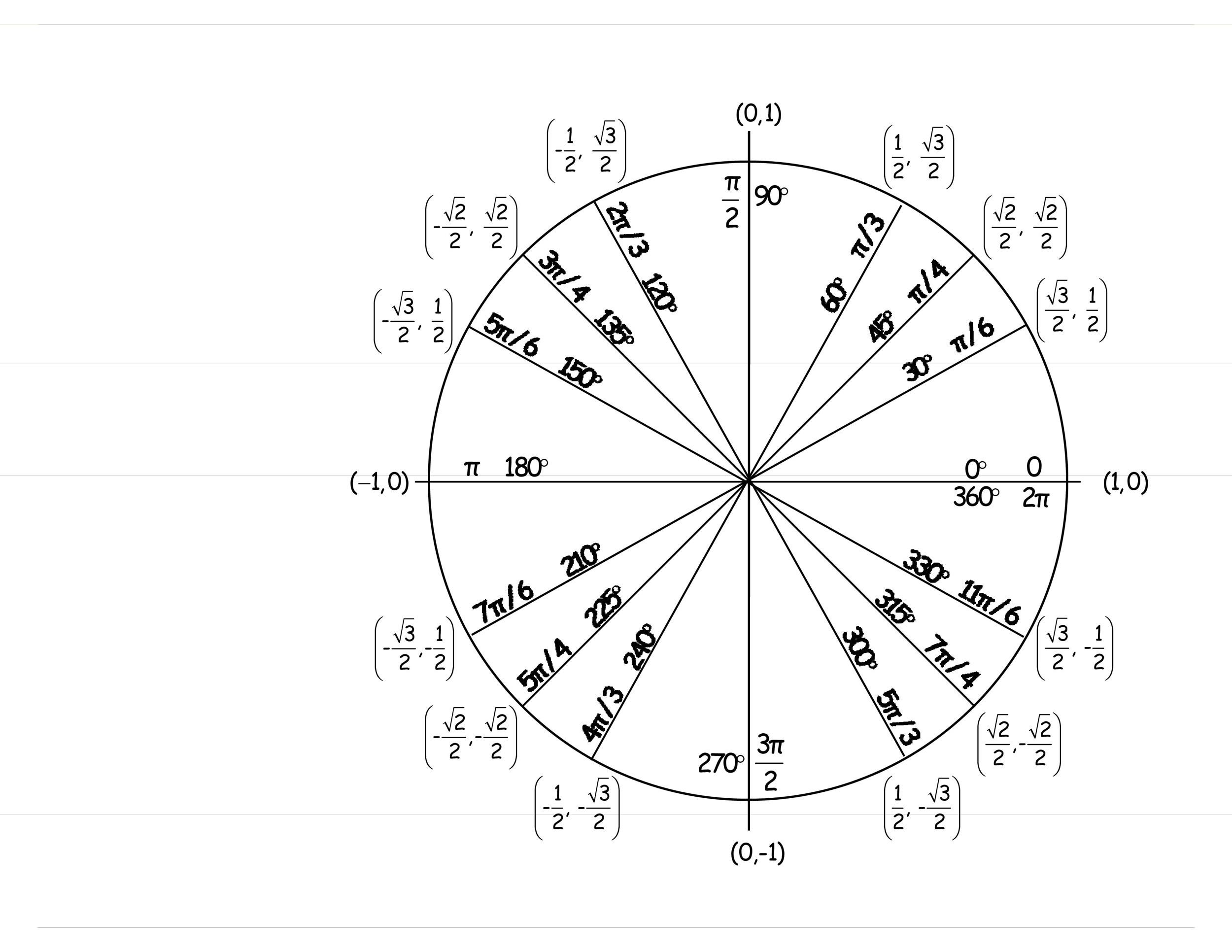
ways that a position can be expressed mathematically

• cartesian system → (x, y) on the x-axis and y-axis

• polar system → (r, theta) where r = dist of the point from the origin, and theta = angle from the pos hori axis

relationship between cartesian coords and polar coords

x = rcos()

y = rsin()

r² = x² + y²

• this relationship is best for when an object moves in an arc or circular path on the cartesian plane

vector

• mathematical object representing a physical quantity that has a magnitude (or MODULUS) and direction

• can rep position, speed, force, etc

• vectors typically look like arrows, with the arrowhead repping the orientation and the length of the arrow repping the modulus (magnitude)

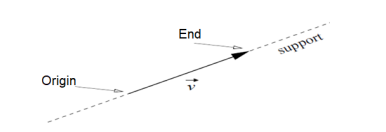
vector notations

you have position/point A = (ax, ay), and position/point B = (bx, by), so you’d find the vector that starts at A and points to B → AB = A - B = (bx - ax, by - ay)

how to calculate scalar magnitude of a vector

two vecs are equal when:

they have the same dir, sense (measured w the same units), and length

the vector directly opposite to BA =

-AB

(opposite dir, same scalar mag)

vectors addition: triangle method

and solve using geometric analysis

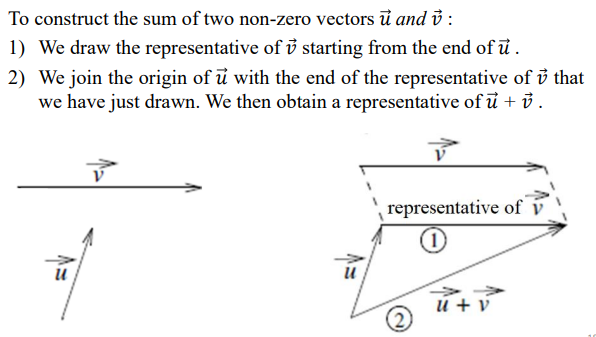
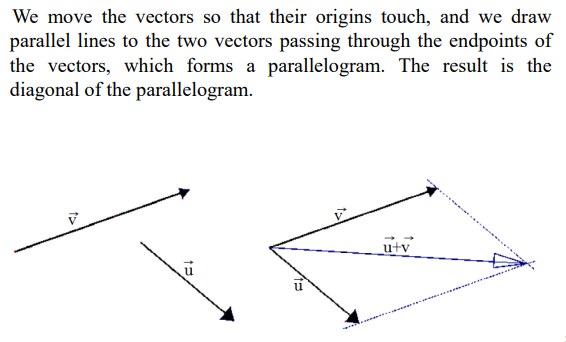
vector addition: parallelogram method

analysis of a triangle: cos law

best for when you have two sides sandwiching an angle

analysis of a triangle: sin law

• best for when you know two angles and one side of a triangle

vector addition: general rule

• add the x-components and the y-components together to get the resulting vector

• if vectors aren’t already given in component form, remember: vec = (vec*cos(), vec*sin()) where the angle is from the pos hori dir

how to extract the direction from a vector:

divide the vector by its norm/magnitude to get the corresponding unit vector

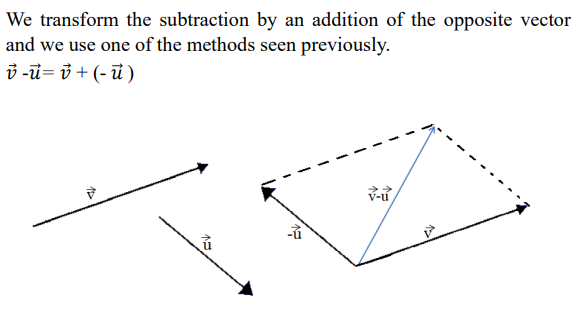
how to approach vector subtraction

always rmbr: a - b = a + (-b), and the “negative” version of a vector is just the same vector but in the opposite dir

vector algebra: adding or subtracting vectors in component form

component form: v = <3, 4> = 3i + 4j, where i and j are unit vectors in the same dir as the hori axis and the vert axis

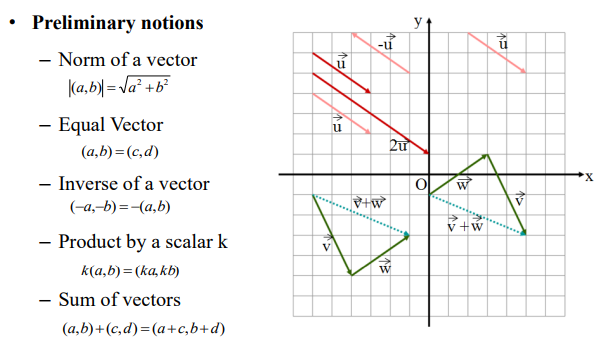
preliminary notions of vectors

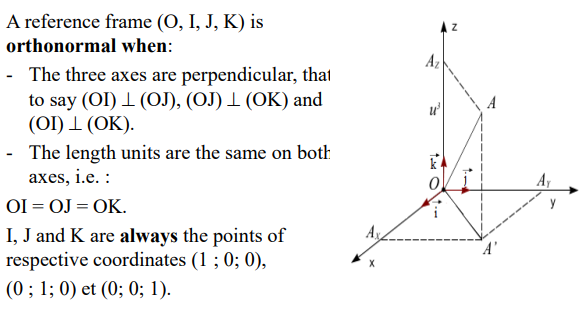
orthonormal reference frame

the 3D cartesion system is an orthonormal ref frame

scalar (or dot) product: definition

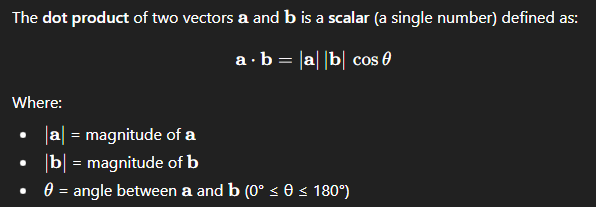
scalar (or dot) product: how to calculate when vecs are in component form

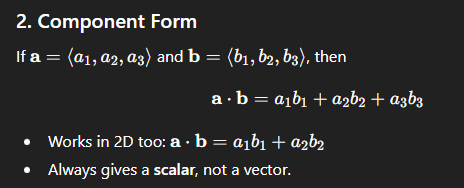
scalar (or dot) product: geometric meaning

properties of scalar (or dot) product

vector (or cross) product: definition

the result of computing cross product with two or three vectors is a vector that’s perpen to both of them