3.4 Finding Z-Score, Percentiles and Quartiles, and Comparing Standard Deviation Theory

Definition of Relative Standing

(1) comparing measures between or within data sets

Z-Score

(1) the number of standard deviations a data value (x) is away from the mean

(2) the number of standard deviations away from the mean

Sample Z-Score Formula

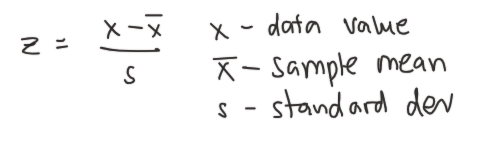
Population Z-Score Formula

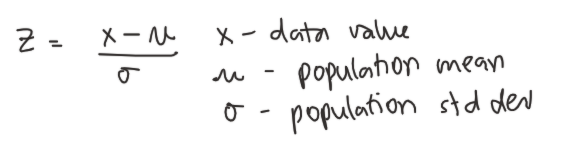
The larger the z-score…

(1) the rarer the data value

What percentage of data is included within a z-score of -1 and 1?

(1) 68% — 68% of your data will lie within 1 standard deviation away from the mean

What percentage of data is included within a z-score of -2 and 2?

(1) 95% — 95% of your data will lie within 2 standard deviations away from the mean

What percentage of data is included within a z-score of -3 and 3?

(1) 99.7% — 99.7% of your data will lie within 3 standard deviations away from the mean

What is considered usual data?

(1) within 1 to 2 standard deviations

What is considered unusual data?

(1) anything beyond 2 standard deviations

Quartiles

(1) break your data up into quarters

How many quartiles exist?

(1) only 3, Q1, Q2 (Median), and Q3

1st Quartile

(1) the data value that represents the bottom 25% of sorted data

2nd Quartile

(1) the data value that represents the bottom 50% of sorted data

(2) also the median

3rd Quartile

(1) the data value that represents the bottom 75% of sorted data

4th Quartile

(1) trick question, there is no 4th quartile because that would include everything

Steps to Calculating Quartiles

Step 1: Sort or order your data values in order

Step 2: Find the median, or Q2 to split your data in half

Step 3: Find Q1 and Q3 by further splitting your median sections in half; find the median of the bottom 50% Q1, find the median for the bottom 100% Q3

Percentiles

(1) break your data up into 100 parts

How many percentiles exist?

(1) 99 percentiles only exist

What do percentiles tell you?

(1) how a value compares to the rest of the group

Steps to Calculating Percentiles

Step 1: Identify your position, the number of how many values below you compared to the total values (how many people did worse)

Step 2: Identify the total number of values there are

Formula for Percentiles

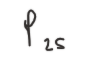
(1) Q1

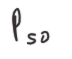
(1) Median

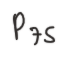
(1) Q3

What does IQR stand for?

(1) interquartile range

Definition of Interquartile Range

(1) the middle 50%

(2) the difference between quartile 3 and quartile 1

Formula for IQR

IQR = Q3 - Q1

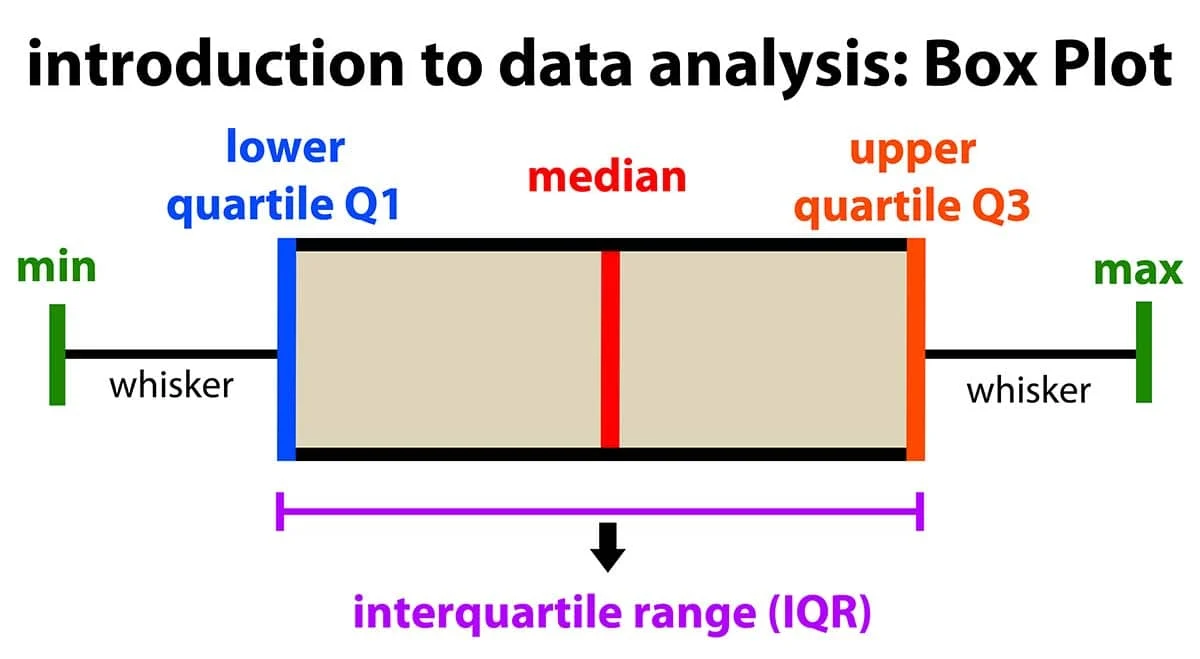
What is a box plot?

(1) a graphic representation of the five number summary

Five Number Summary

(1) composed of 5 specific values

• Minimum Value

• Q1

• Median (Q2)

• Q3

• Maximum Value

Steps to Organize A Box Plot

Step 1: Organize and sort your data set

Step 2: Find the 5 number summary

• Minimum Value

• Maximum Value

• Median (Q2)

• Q1

• Q3

Step 3: Make a number line and plot the five number summary to scale according to the number line

Step 4: Draw a box around Q1, Q2, Q3

Steps to Calculate Outliers

Step 1: Find IQR, Q3 - Q1

Step 2: Multiply IQR by 1.5 (1.5 × IQR)

Step 3: Take (1.5 × IQR):

• Subtract that number from Q1

• Add that number from Q3

Step 4: Analyze — anything outside of that number or range is mathematically an outlier

What does a box plot look like?