A-Level Complex Numbers

exponential form

(r)e^iθ

argument of a real number

-π, 0, π

argument of imaginary number

π/2, -π/2

expression for cosθ

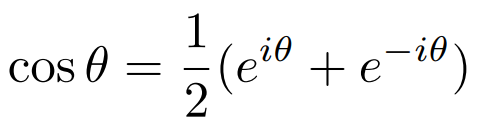
expression for sinθ

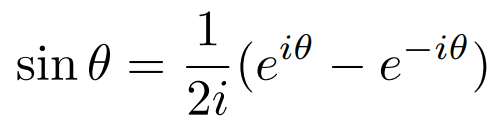
derive the expression for cosθ from Euler’s relation

derive the expression for sinθ from Euler’s relation

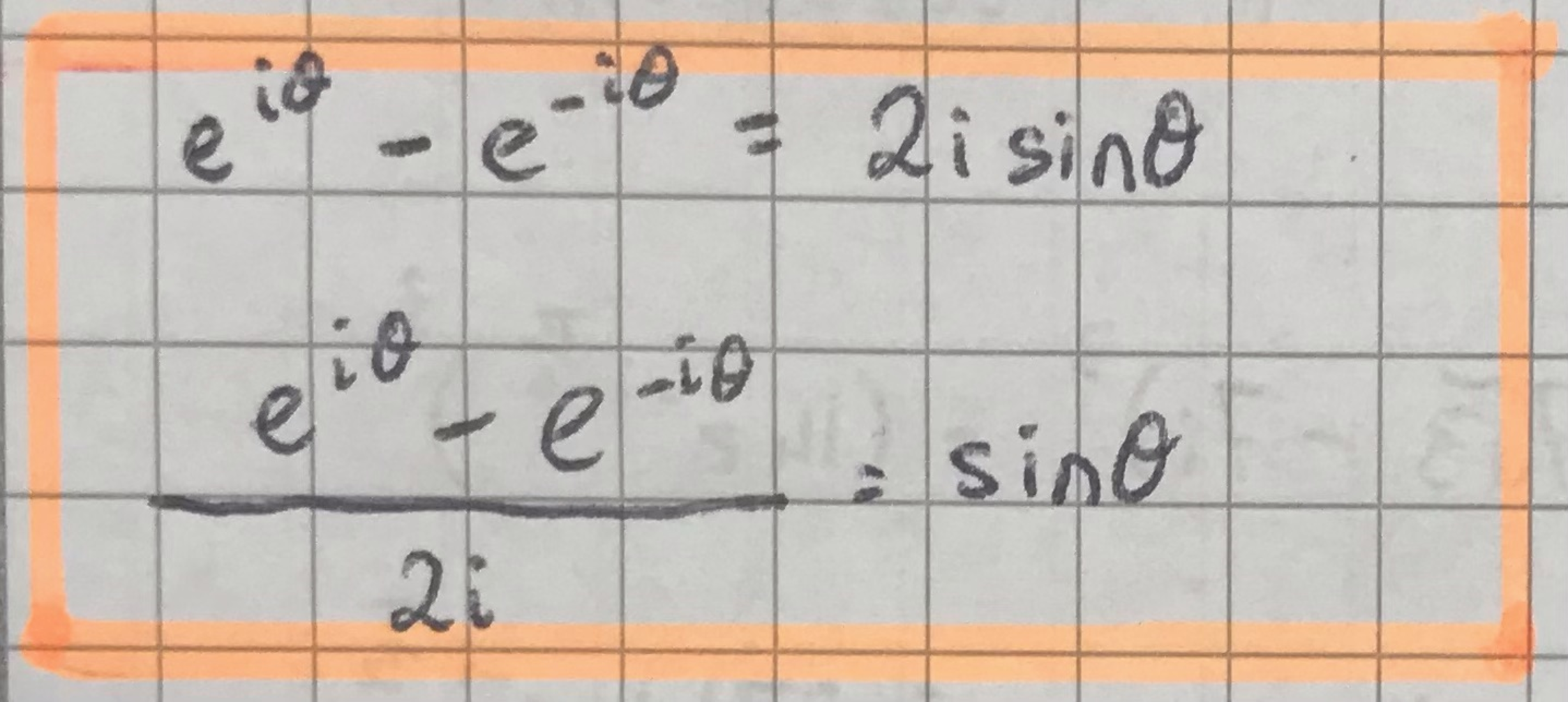
how to derive a formula for sin(nθ) and cos(nθ)

• cos(nθ)+isin(nθ) = (cosθ+isinθ)ⁿ (de Moivre’s theorem)

• expand this bracket (let cosθ=c and sinθ=s for ease of layout)

• the real parts are cos(nθ) and the imaginary parts are sin(nθ)

how to change cosⁿx/sinⁿx into an integrable form and what is this form

• form is sum of multiple angles

• express trig function in exponential form

• let e^iθ = z so that

• cosⁿ(θ) = (½)ⁿ[z+(1/z)]ⁿ
  sinⁿ(θ)=(1/2i)ⁿ[z-(1/z)]ⁿ

• expand this using binomial expansion

• gather inverse terms together

• zⁿ±(1/zⁿ)= 2cos(nθ)/2isin(nθ) - de Moivre

• done!

how to turn a combination of sin and cos into an integrable form

same procedure as above, but include difference of two squares to make calculations easier

integral of cos(nθ)

(1/n)sin(nθ)

integral of sin(nθ)

(-1/n)cosnθ

when to employ “the trick”

when there is a 1±e^iϕ

what is “the trick”

for 1±e^iϕ, multiply the whole expression by e^(-iϕ/2) over itself

what to do when something isn’t “trickable”

for n±k(e^iϕ), multiply by n±k(e^-iϕ) [ie the complex conjugate] over itself

how to find sums of trig series for cos and sin, given one of the series

• find the corresponding cos/sin series

• find cos+i sin

• convert into exponential form to form geometric series

• apply formula then manipulate it (using trick or non-trick)

• sum of cos series is real part/ sum of sin series is imaginary part

what to do for trig series with binomial coefficients

• C + iS

• convert to exponential form (still with binomial coefficients)

• figure out what bracket is being expanded

• apply “the trick” to the bracket and manipulate

• apply the power to each term in the bracket

• cos series is real part/ sin series is imaginary part

the nth roots of unity are

1, e^i(2π/n), e^i(4π/n),……, e^i(2(n-1)π/n)

how to find the nth roots of a number (two different ending methods) ie how to solve zⁿ=w

• express equation as rⁿe^inθ=Re^iϕ

• solve rⁿ=R (r must be positive as r=|z|)

• solve nθ=ϕ

• either solve up to nθ=ϕ+2(n-1)π

• or let ω=e^i2π/n and x=ₙ√R e^iϕ/n, then the roots are x, xω, xω²….xωⁿ⁻¹