Calculus (IB)

Flashcards for differentiation and integration.

Differentiation

The process of finding the derivative of a function, which represents the rate of change of the function at a given point.

Derivative of a Function

The derivative measures how the function's output changes concerning its input.

Power Rule

If 𝑓(𝑥) = 𝑥^𝑛, then 𝑓'(𝑥) = 𝑛𝑥 ^𝑛^-^1.

Product Rule

If 𝑓(𝑥) = 𝑔(𝑥) * ℎ(𝑥), then 𝑓'(𝑥) = 𝑔'(𝑥) * ℎ(𝑥) + 𝑔(𝑥) * ℎ'(𝑥).

Quotient Rule

If 𝑓(𝑥) = 𝑔(𝑥) / ℎ(𝑥), then 𝑓'(𝑥) = (𝑔'(𝑥) * ℎ(𝑥) - 𝑔(𝑥) * ℎ'(𝑥)) / [ℎ(𝑥)]^2.

Chain Rule

If 𝑓(𝑥) = 𝑔(ℎ(𝑥)), then 𝑓'(𝑥) = 𝑔'(ℎ(𝑥)) * ℎ'(𝑥).

Implicit Differentiation

A technique used to find the derivative of an implicitly defined function.

Integration

The process of finding the antiderivative of a function.

Indefinite Integrals

Represent a family of antiderivatives or primitives of a function.

Definite Integral

Represents the area between the graph of the function and the x-axis.

Higher Order Derivative

Finding the rates of change of rates of change.

Integration Technique: Substitution

Substituting a new variable to simplify the integrand.

Integration Technique: Integration by Parts

Applying the product rule for differentiation in reverse.

Integration Technique: Partial Fractions

Used for rational functions by decomposing them into simpler fractions.

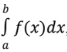
What terms represent the limits of integration?

a and b