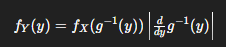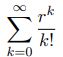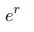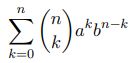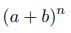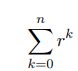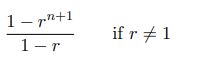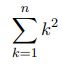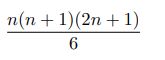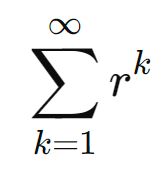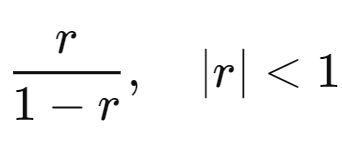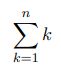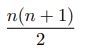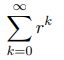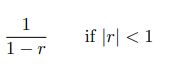Statistics: Exponential, Uniform, Normal, Bernoulli, Binomial, Geometric, Poisson Distributions

PDF for exponential distribution

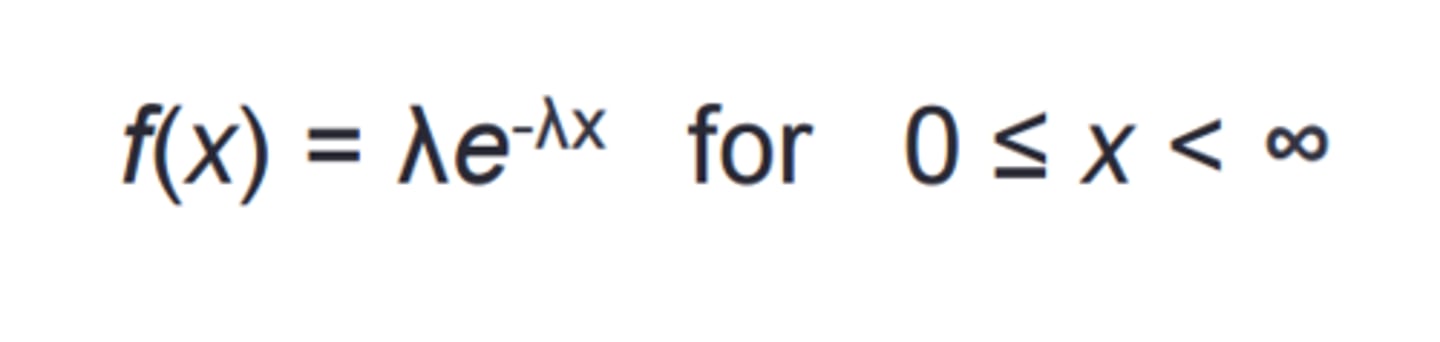
CDF of exponential

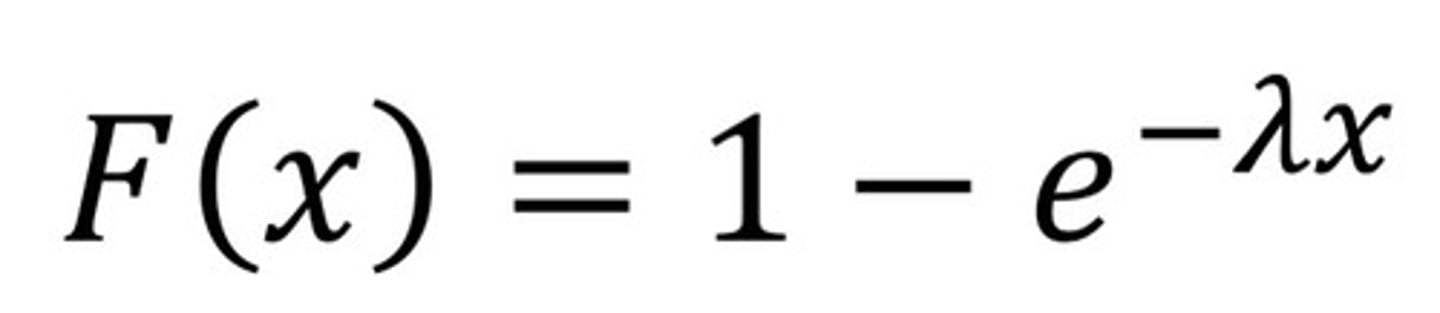
Expected Value of Exponential Distribution

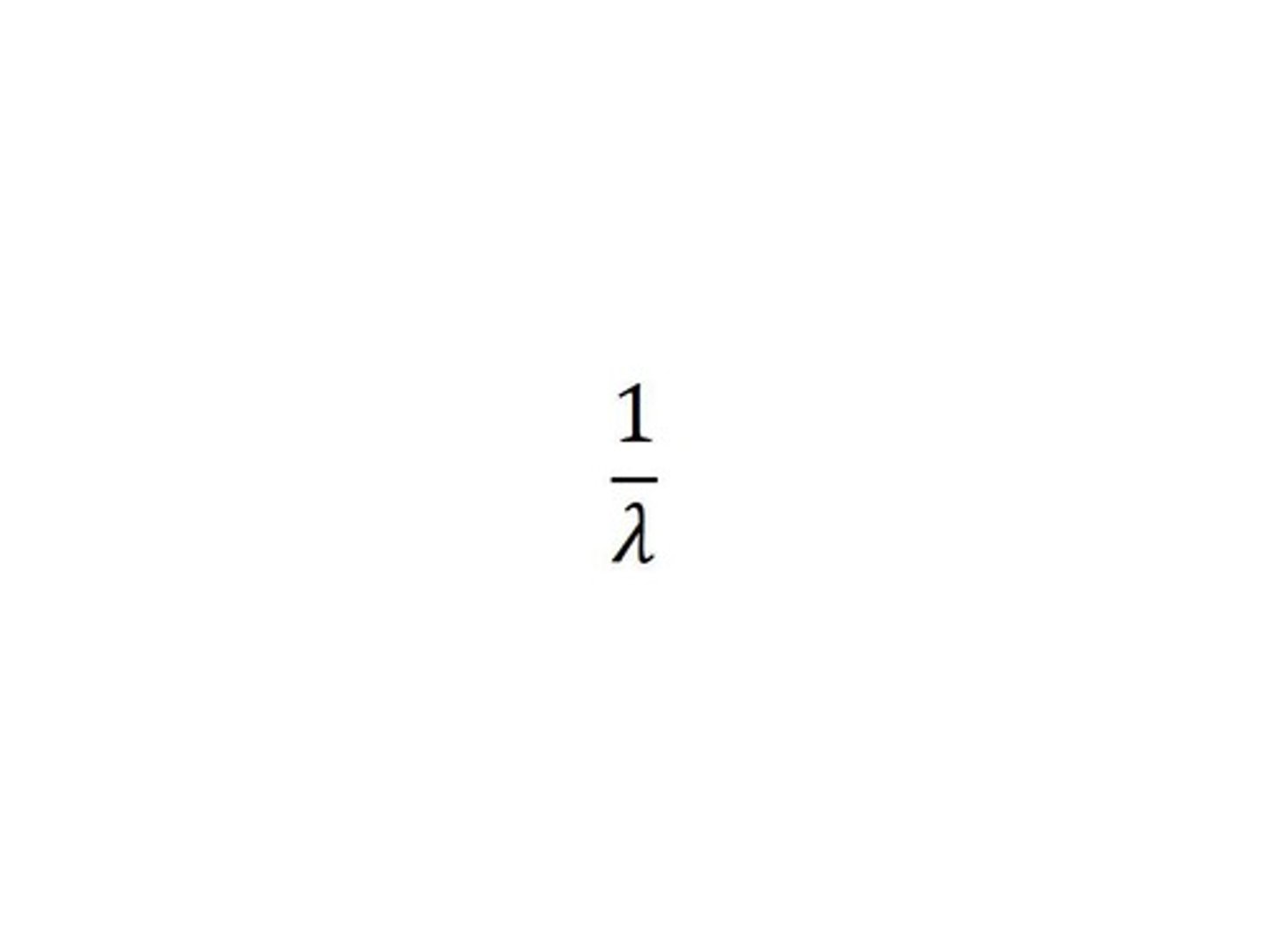
Variance of Exponential Distribution

1/(λ^2​)

PDF of Uniform Distribution

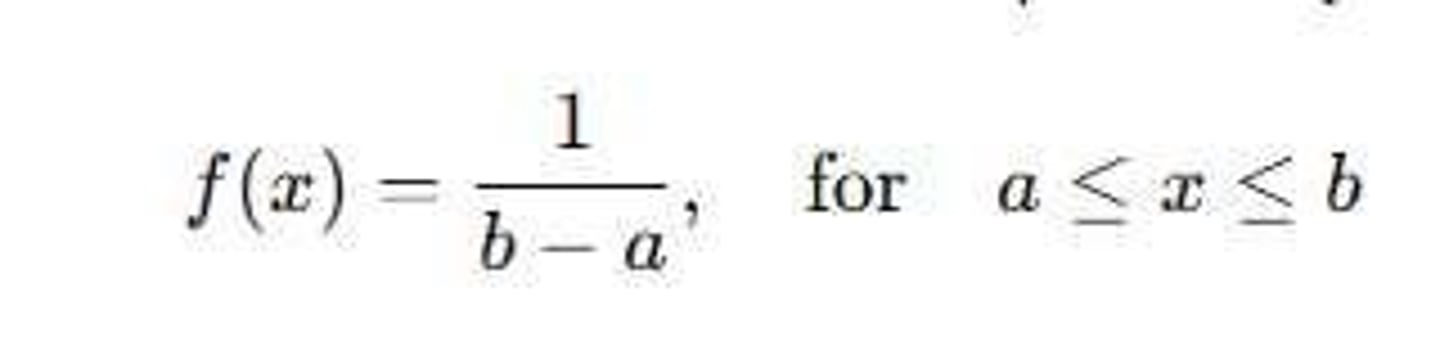
CDF of Uniform Distribution

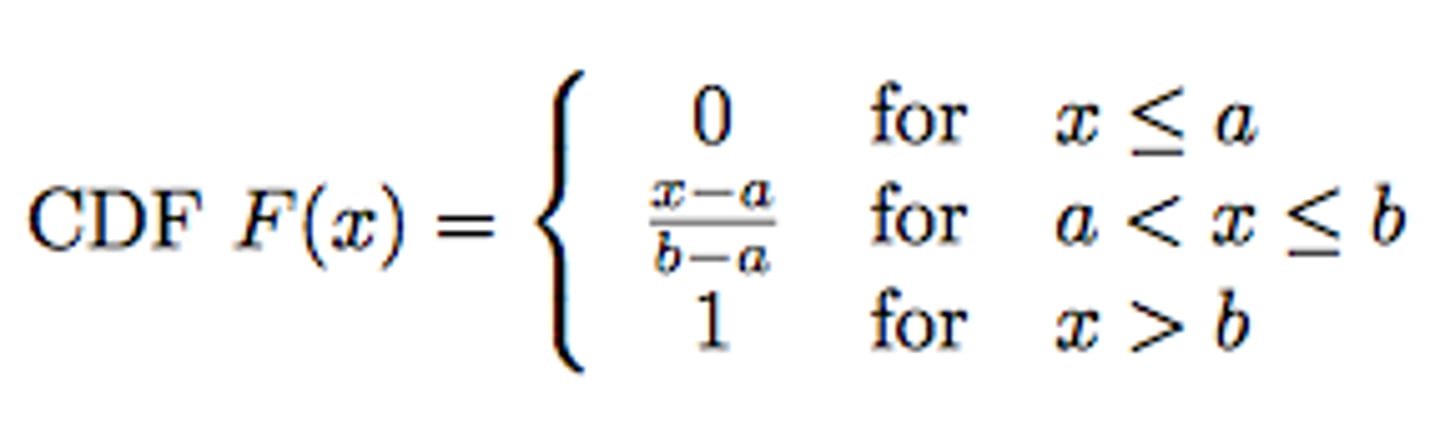
Expected Value of Uniform Distribution

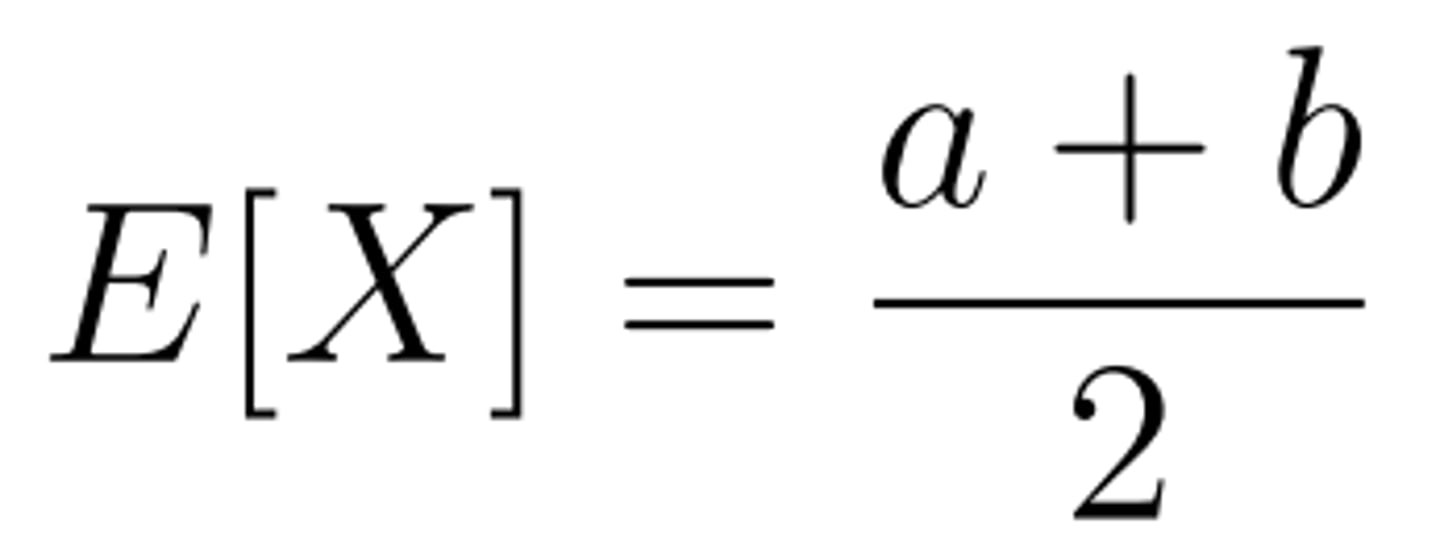
Variance of Uniform Distribution

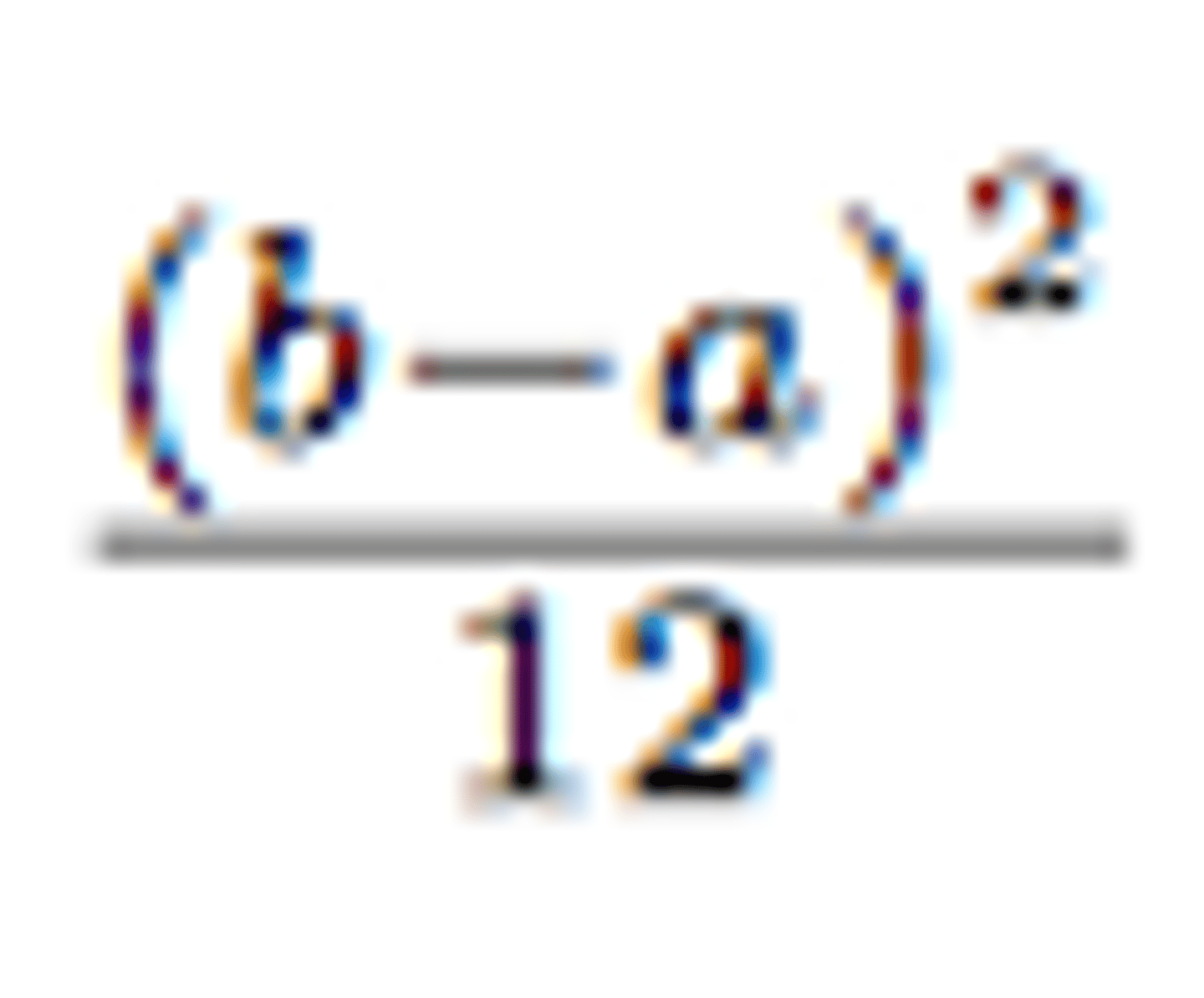
Expected Value of Normal Distribution

μ = mean (center of the curve)

Median of Normal Distribution

μ = mean (center of the curve)

What's the probability that one exponential distribution (A) is less than another (B)

P(Ta < Tb) = (λa)/(λa+λb)

Expected Value of Bernoulli

p

Expected Value of Binomial

np

Expected Value of Geometric

1/p

Expected Value of Poisson

λ

Variance of Poisson

λ

Variance of Bernoulli

p(1-p)

Variance of Bionomial

np(1-p)

Variance of Geometric

(1-p)/p^2

PMF of Bernoulli

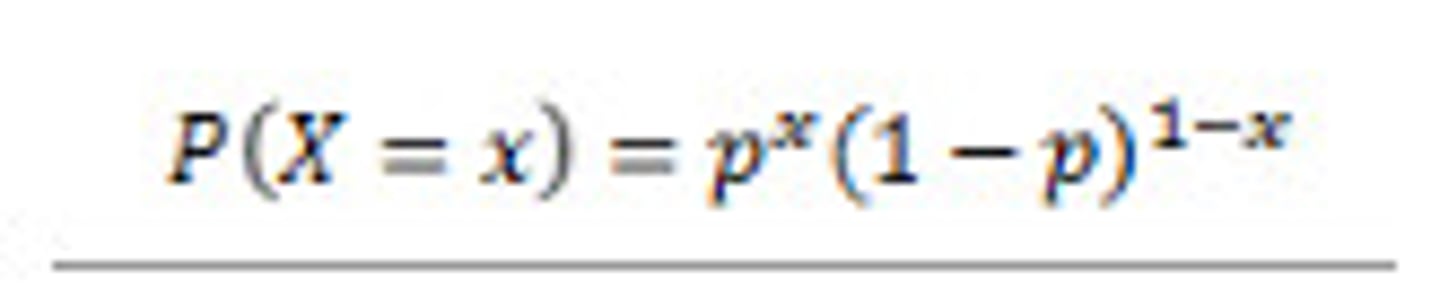
PMF of Binomial

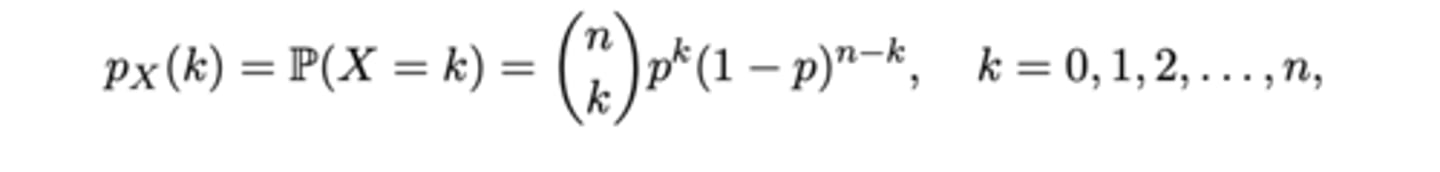
PMF of Geometric

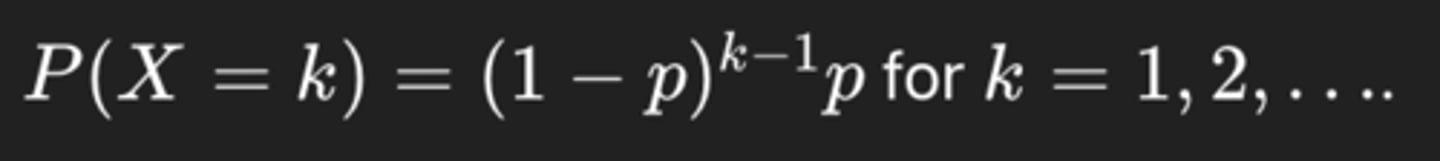
PMF of Poisson

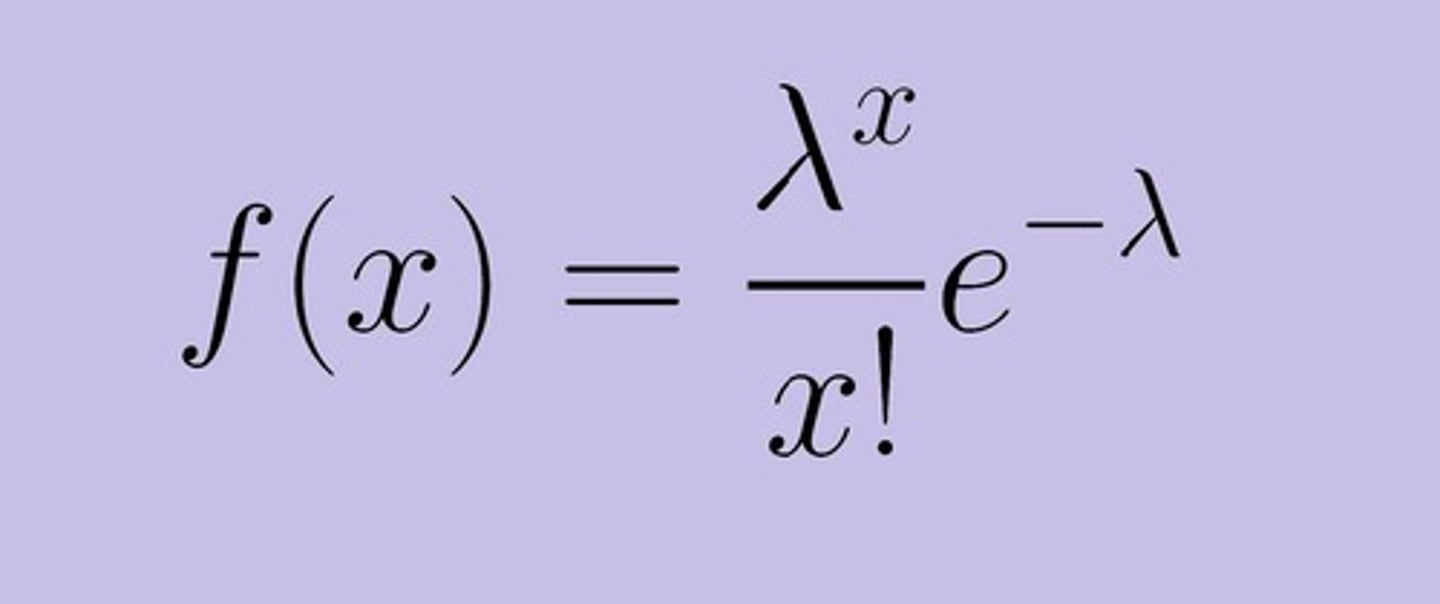
What does Z represent

How many standard deviations away X is from the mean

How to compute Z

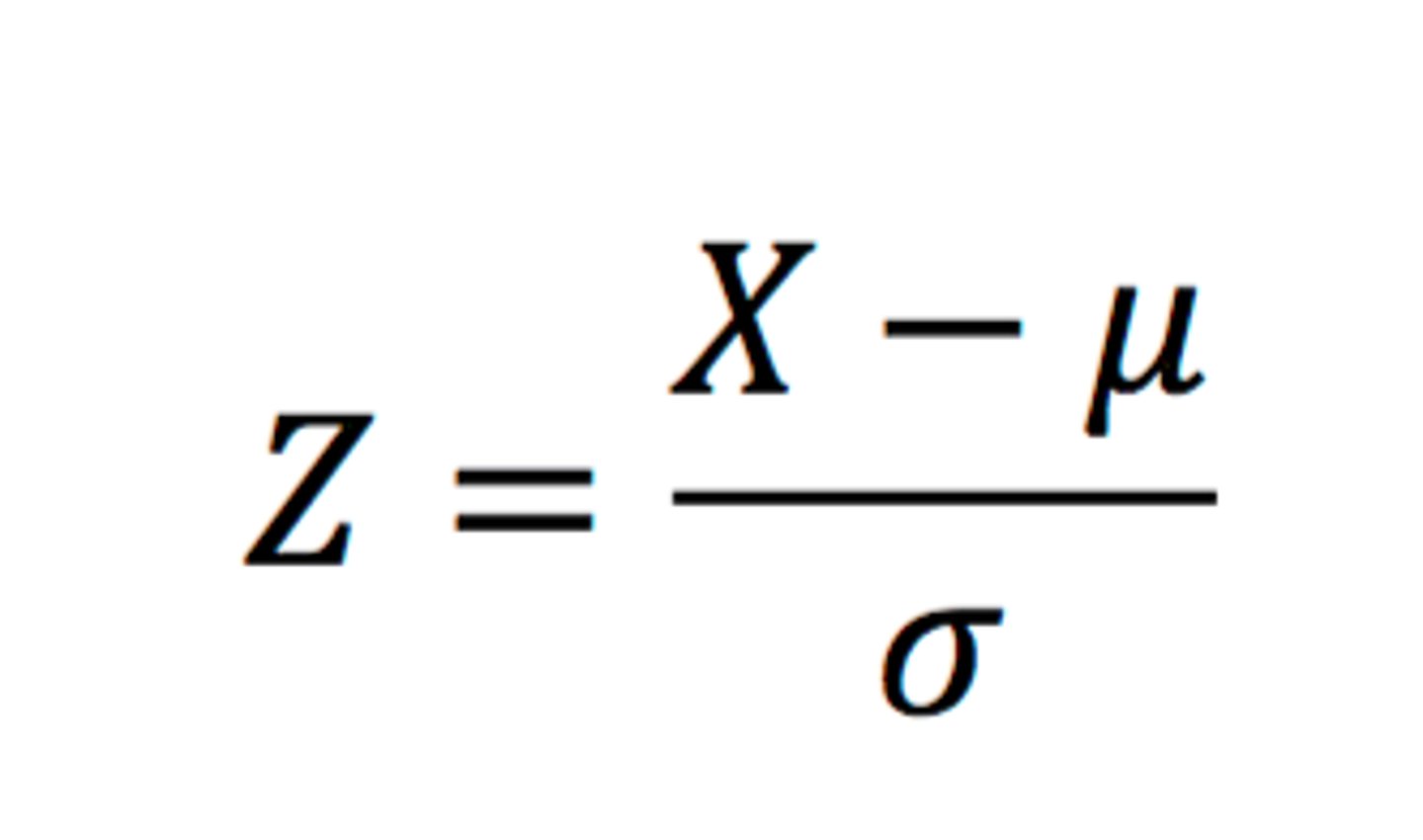
What are the percentages of data within 1, 2, and 3 standard deviations of the mean in a standard normal distribution?

68% within ±1σ

95% within ±2σ

99.7% within ±3σ

What is CV

How spread out the data is compared to the average

CV formula

σ​/μ

SCV Formula

Var(x)/(E[x]^2)

What is SCV

Shows randomness

How do you find Fy(Y) when you know Y = g(x) and Fx(X) (given g(x) is strictly increasing)

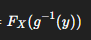
How do you find Fy(Y) when you know Y = g(x) and Fx(X) (given g(x) is strictly decreasing)

Fy​(Y)=1−Fx​(g−1(Y))

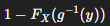
Formula for Cov(x,y)

E[XY] − E[X]E[Y]

Cov(x,x)

Var(x)

Cov(x,c) where c is a constant

0

Cov(x+y,z)

Cov(x,z) + Cov(y,z)

Cov(aX+b,cY+d)

acCov(X,Y)

Markov's Inequality

P(X ≥ t) ≤ E(X)/t

Chebyshev's inequality (Standard Deviation)

P(|X − μ| ≥ kσ) ≤ 1 / k²

Chebyshev's inequality

P(|X − μ| ≥ t) ≤ Var(X) / t²

What formula gives the pdf of Y = g(x) when g(x) is one-to-one and you know FX​(x)?