Base Ten and Fractions

Scientific Notation

numbers expressed as the product of a base-10 number and a number between 1 and 10

Example:

2.56 x 10 = 25.6

4.32 x 10-4 = 0.000432

Non-proportional Manipulatives

objects that are not proportional to each other with respect to shape and size. Often, all of the items are the same size.

Example:

Counting Tokens

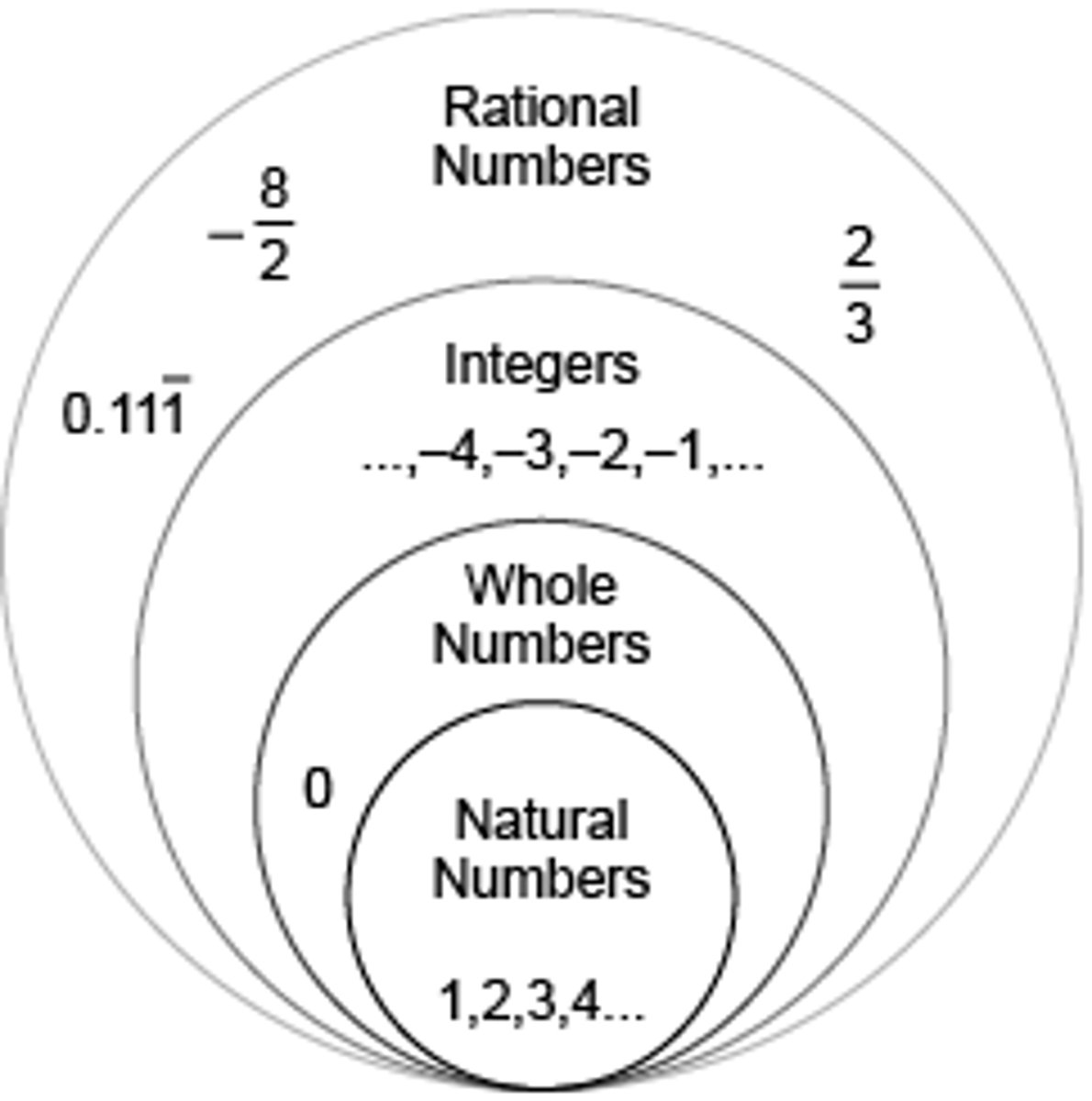
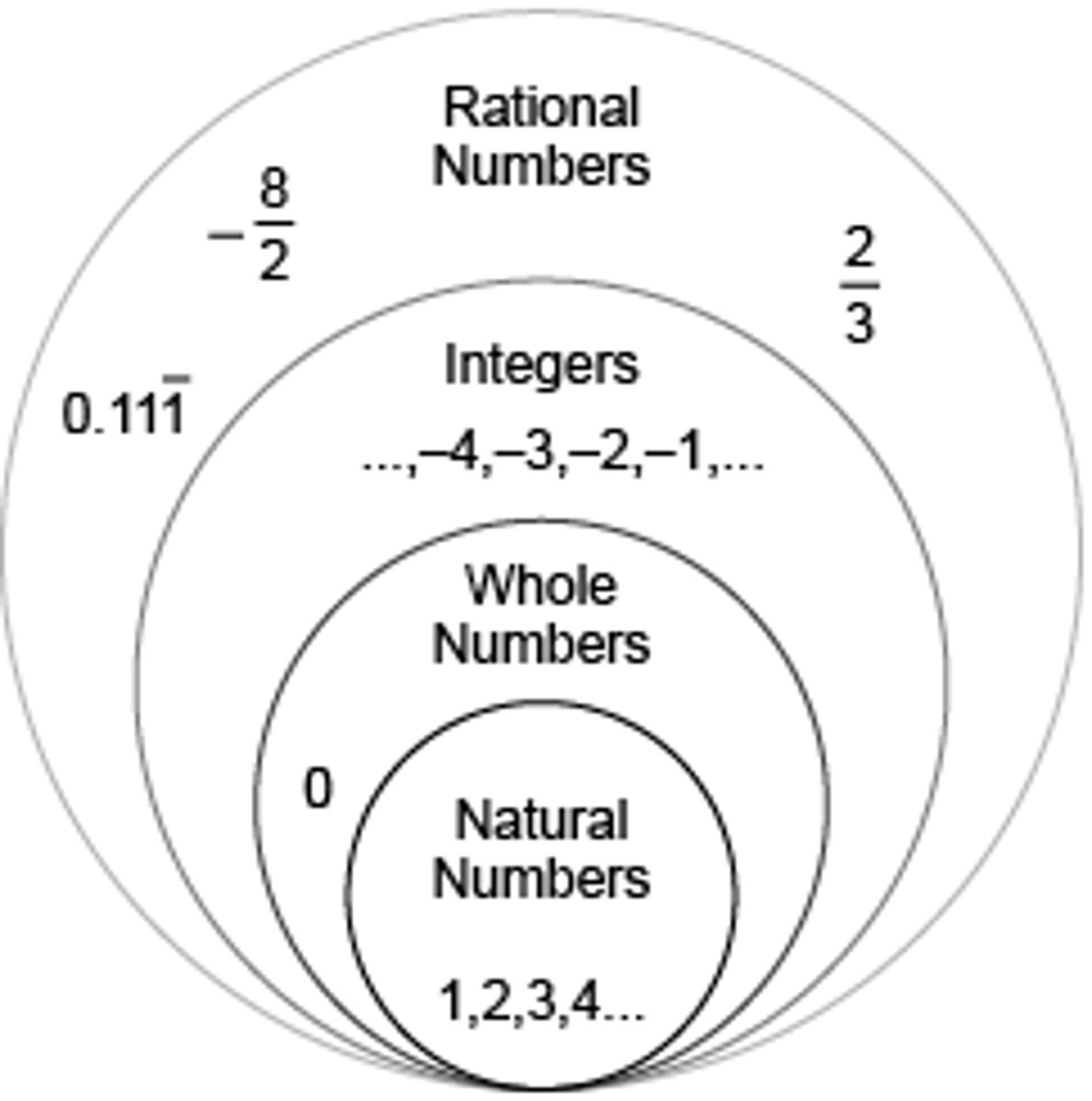
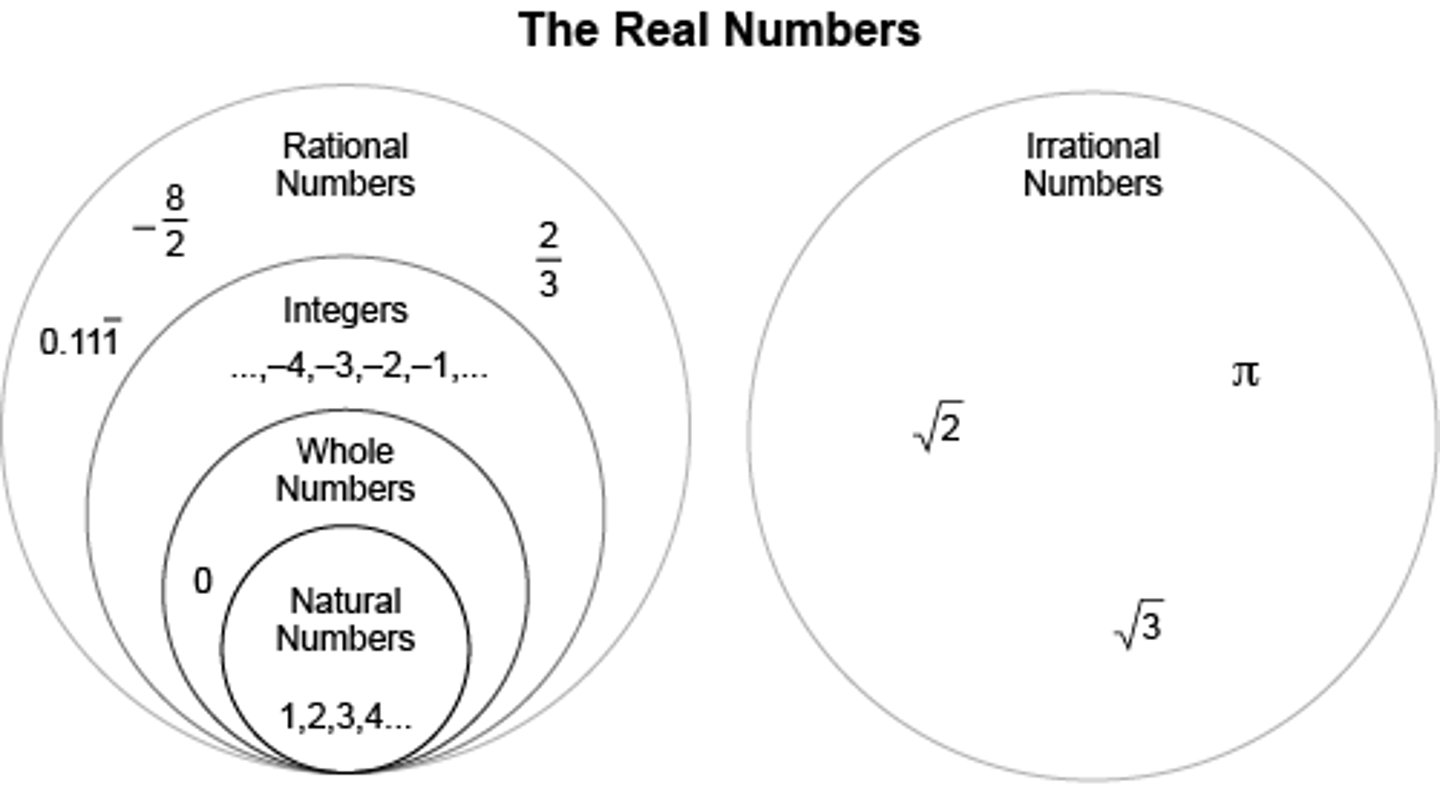
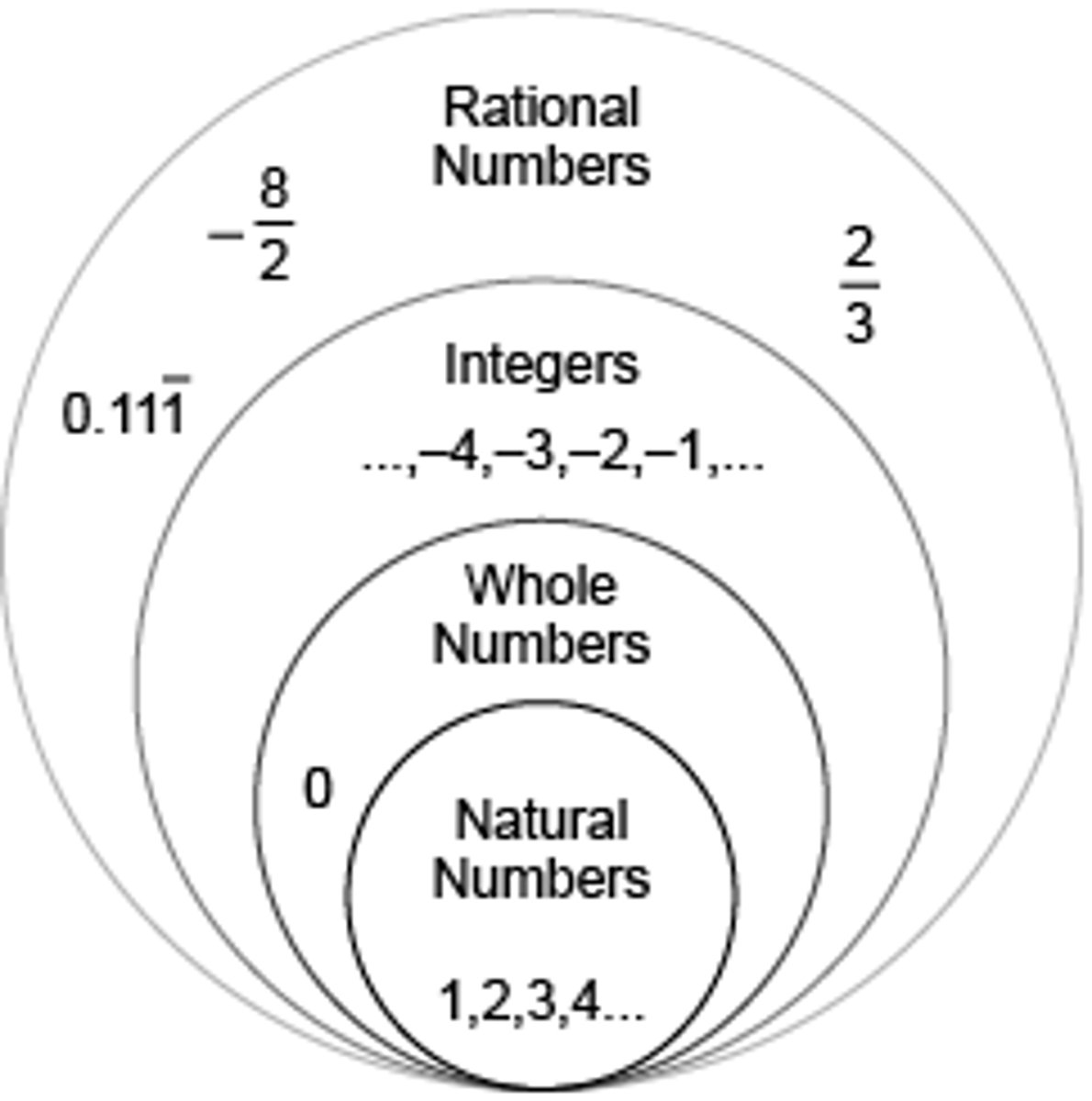
Natural Numbers

set of counting numbers starting at 1 and increasing by 1s up to infinity; sometimes called "counting numbers"

Example:

1, 2, 3, 4....

Number Line

a straight line where each number is equal distance from the next one

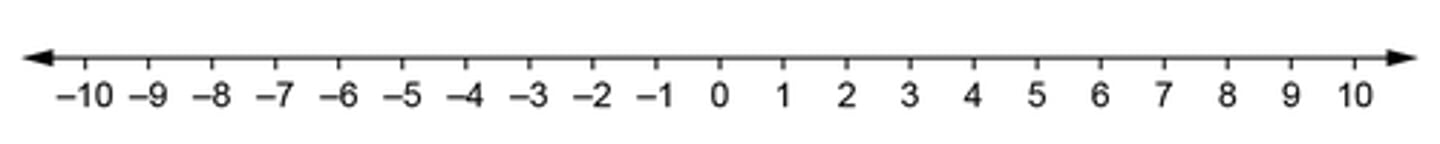
Sum

the result of adding two or more numbers, a total

Example:

addend + addend = sum

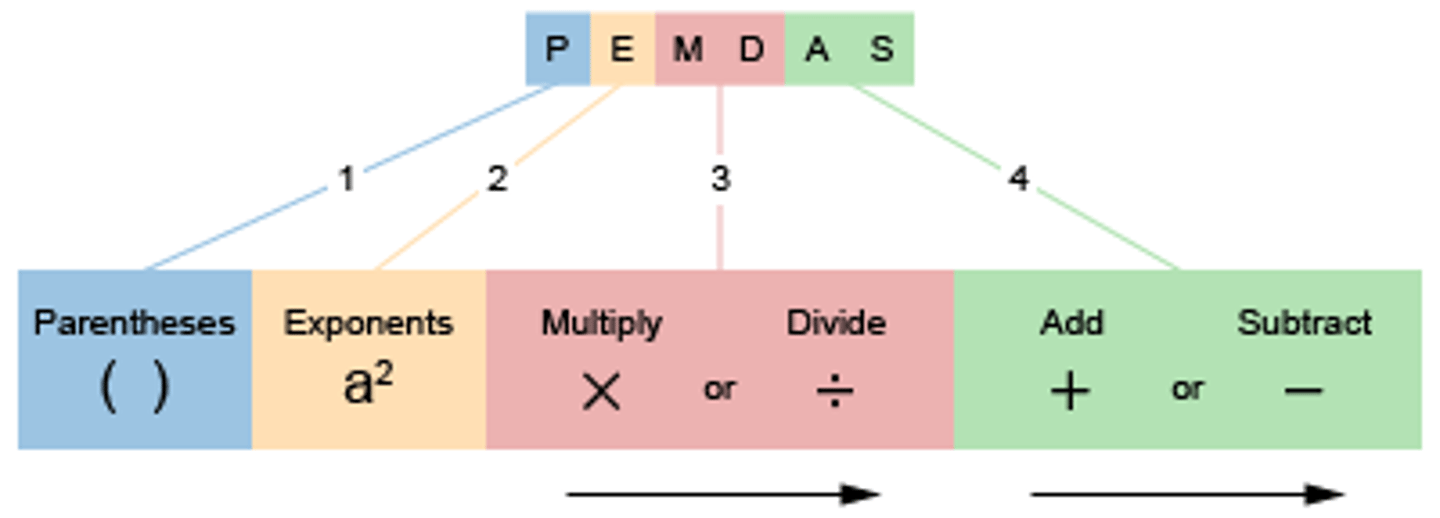
Order of Operations (PEMDAS)

the set order in which multi-step equations must be solved: Parenthesis, Exponents, Multiplication and Division (left to right), Addition and Subtraction (left to right)

Addend

a number that is added to another number

Example:

addend + addend = sum

Dividend

A number that is divided by another number (divisor) to find the quotient

Example:

dividend ÷ divisor = quotient

Rounding

A number is simplified to its closest multiple of 10, 100, 1,000, etc.

Example:

26 rounds UP to 30

Integers

infinite set of positive and negative counting numbers and zero

Example:

–2, –1, 0, 1, 2

Concrete Operational Stage

the third stage of Piaget's Theory of Cognitive development, occurring from 7 years old to adolescence, in which children begin to think logically and use inductive reasoning

Least Common Multiple (LCM)

the smallest number that is a multiple of two or more numbers; the smallest number two or more numbers will divide into evenly

Example:

For 12 and 15, LCM = 60

Multiples of 12: 12, 24, 36, 48, 60

Multiples of 15: 15, 30, 45, 60

Expanded Form / Expanded Notation

break apart each digit in the number and show the digits' true value

Example:

4,358→4000+300+50+8

Irrational Numbers

real numbers that CANNOT be represented exactly; they can not be shown as a ratio of two integers nor placed on a number line

Example:

pi (π)

Greatest Common Factor (GCF) / Greatest Common Divisor (GCD)

the greatest factor that is common to two or more numbers; the largest number that will divide evenly into two or more numbers

Example:

For 12 and 15, GCF = 3

Factors of 12: 1, 2, 3, 4, 6, 12

Factors of 15: 1, 3, 5, 15

Improper Fraction

A fraction where the numerator is larger than the denominator

Example:

3/2

Closure Property

The sum of two real numbers is a real number.

The product of two real numbers is a real number.

Example:

2.5+3=5.5

Reciprocal Fraction

the inverse or "flip" of a fraction in which the numerator and denominator switch places

Example

1/2 → 2/1

Quotient

The result of dividing two numbers

Example:

dividend ÷ divisor = quotient

Fraction Decomposition

Breaking down a fraction into smaller fractions that total to the original

Example:

2/3 = 1/3 + 1/3

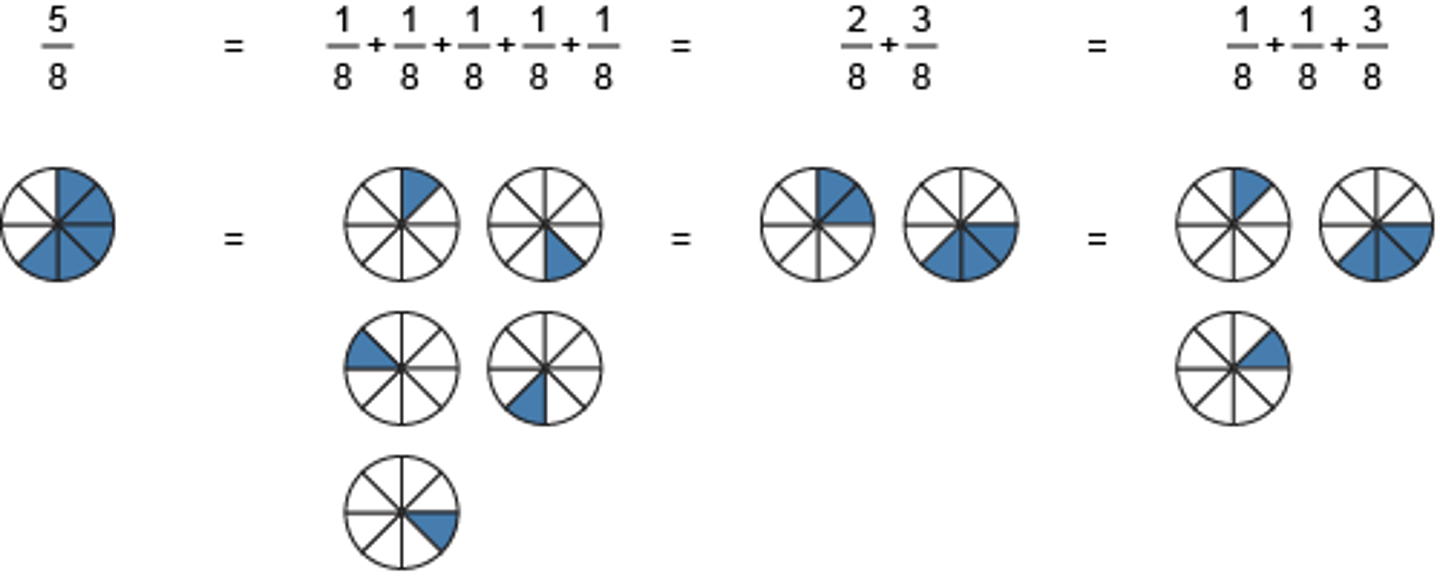
Divisor

A number that divides another number (dividend) to find the quotient

Example:

dividend ÷ divisor = quotient

Commutative Property

An operation is commutative if changing the order of terms does not change the outcome

Example:

a+b=b+a

Factors

Values that are multiplied to get another number.

Example:

Some factors of 12 are 3 and 4 because 3 × 4 = 12

3×4=12

Zero Product Property

When a real number is multiplied by 0, the result is 0.

Example:

5 x 0 = 0

Associative Property

An operation is associative if regrouping the terms does not change the outcome

Example:

(a + b) + c= a + (b + c)

Real Numbers

numbers that have a specific value

Example:

-2, 3, 1/2, 3.2, √2

Whole Numbers

Infinite set of natural numbers and zero

Example:

0,1,2,3, ...

Base 10 Number System

Our number system. Each place location for a number has a value that is a power of 10

Example:

10, 100, 1000, 10000

Numerator

the top term of a fraction

Proportional Manipulatives

objects that are proportional to each other with respect to shape and size

Example:

Tangrams

Difference

the result of subtracting one number from another

Example:

x − y = difference

Unit Fraction

a fraction composed of 1 over any rational number; the inverse of a whole number

Example:

1/2 or 1/19

Multiplicative Identity Property

a number that, when multiplied by x, yields x. These are one or forms of one such as x/x

Example:

6 x 1 = 6​

Benchmark Fraction

an easily remembered fraction that can be used to make problems simpler

Example:

1/10, 1/4, 1/2, etc.

Fraction Composition

Adding fractions to come up with a larger one

Example

1/4 + 1/4 + 1/4 = 3/4

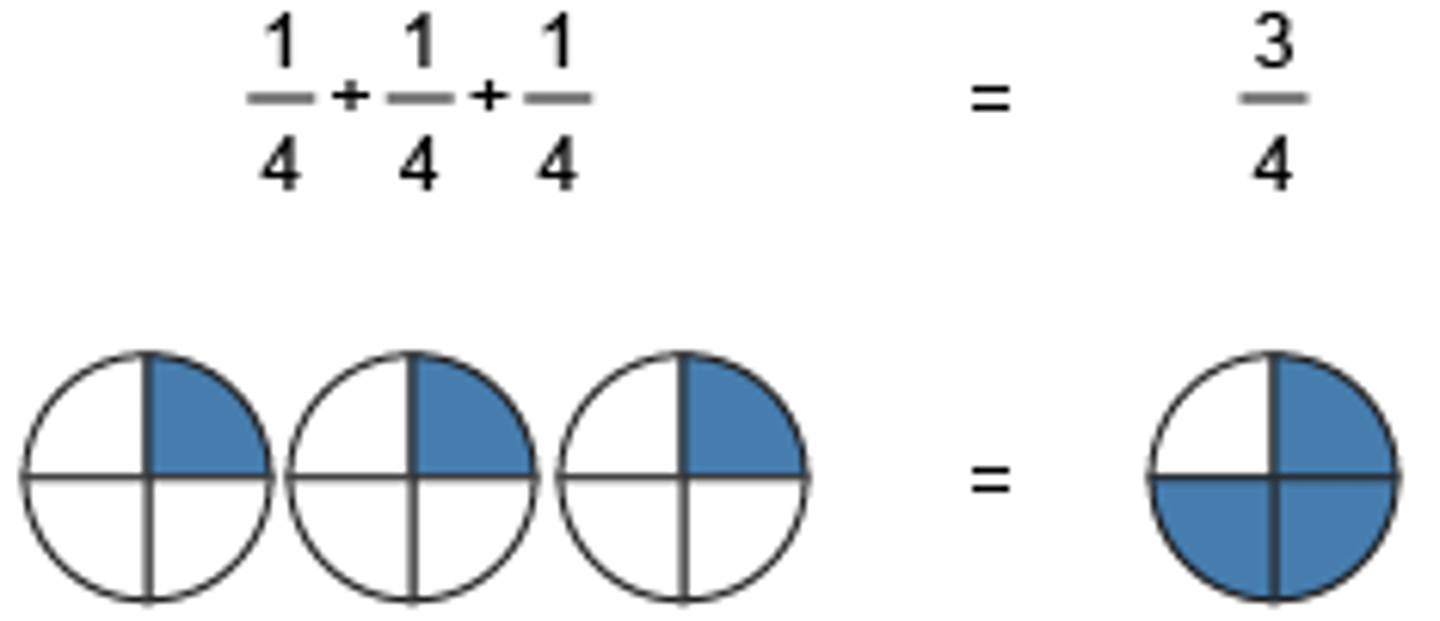
Denominator

the bottom term of a fraction

Mixed Number

A whole number with a fraction

Example:

3 1/2

Distributive Property

a number in front of a group of terms will multiply all terms in the grouping individually

Example:

a(b + c) = ab + ac

Manipulatives

objects used by students to illustrate and explore mathematical concepts, such as to represent numbers in an equation

Example:

Blocks, Coins

Multiplier

a number that multiplies another number (multiplicand)

Example:

multiplicand × multiplier = product

Common Denominator

when 2 fractions share the same total parts of whatever item or items are being represented

Example:

1/3 and 2/3

Multiplicand

a number that is multiplied by another number (multiplier)

Example:

multiplicand × multiplier = product

Additive Identity Property

a number that, when added to any element x in a set, always yields x. Zero itself is sometimes referred to as the additive identity.

Example:

5+0=5

Product

the result of multiplying two or more numbers

Example:

multiplicand × multiplier = product