Complex Numbers and Argand Diagrams

modulus-argument form

z = r(cosθ + isinθ) where |z| = r arg z = θ

exponential form

z=re^iθ

rules for multiplying/dividing complex numbers in mod-arg/exponential form

multiply moduli, add arguments (or the reverse)

what does the locus |z-(x+iy)|=n represent

a circle of radius n, with centre (x,y)

what does the locus |z-(x+iy)|=|z-(a+ib)| represent

the perpendicular bisector of the line between (x,y) and (a,b)

what does the locus arg(z-(x+iy))=θ represent

a "half line" starting from (x,y) and going at the angle θ from the positive real axis

first step in finding the min/max modulus of circle loci

find the line that goes through the centre and the origin

first step in finding min/max argument of circle loci

draw a tangent to the circle that passes through the origin (considering negative arguments)

how to find min modulus of the perpendicular bisector loci

find the modulus of the intersection point between the locus line and the line perpendicular to that which passes through the origin

how to eliminate -isinθ

change both θs into (-θ)

exponential form

re^iθ

θ in radians

argument of a real number

-π, 0, π

argument of imaginary number

π/2, -π/2

expression for cosθ

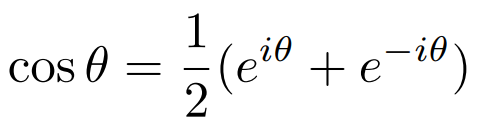
expression for sinθ

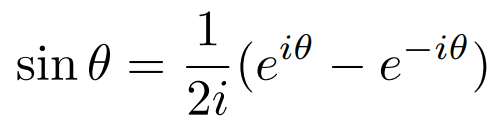
derive the expression for cosθ from Euler’s relation

derive the expression for sinθ from Euler’s relation

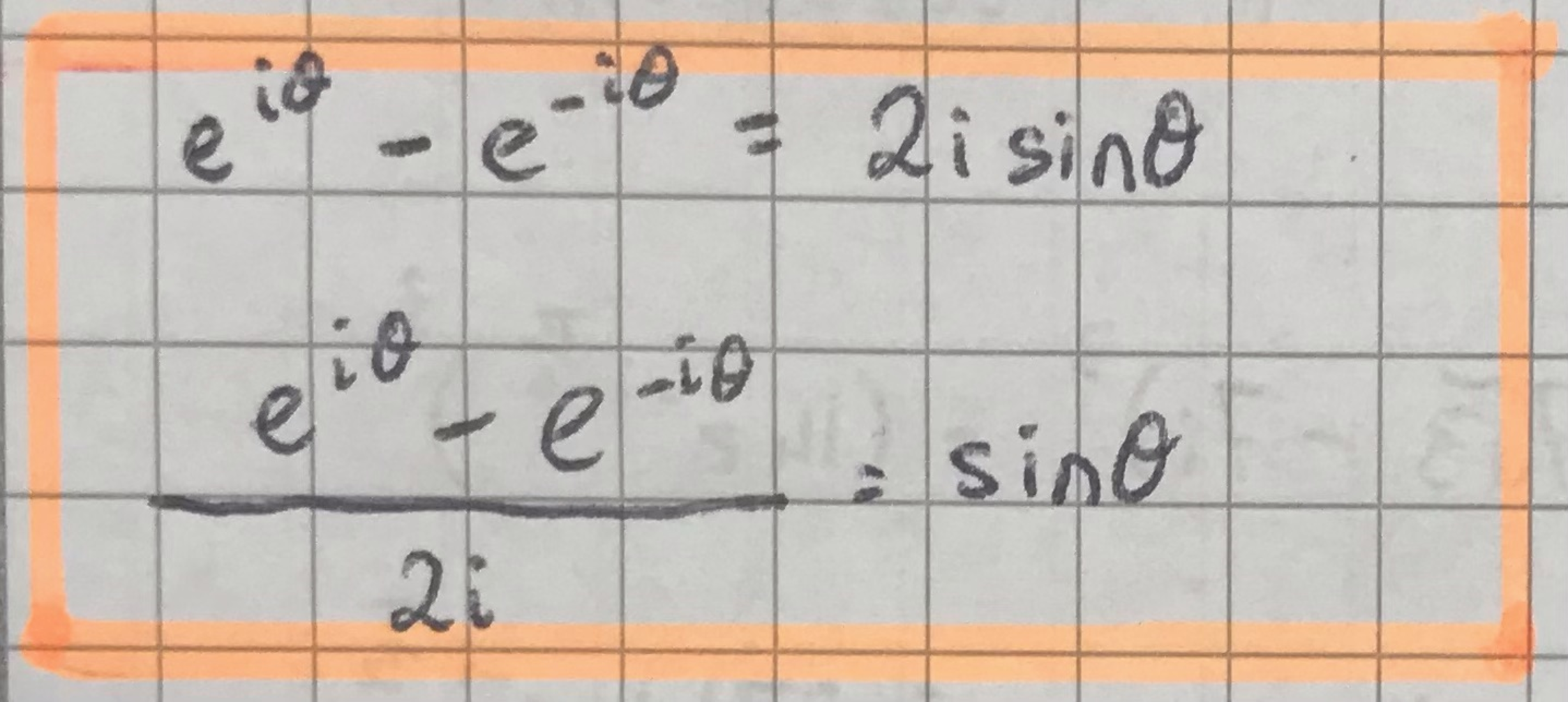
how to derive a formula for sin(nθ) and cos(nθ)

• cos(nθ)+isin(nθ) = (cosθ+isinθ)ⁿ (de Moivre’s theorem)

• expand this bracket

• the real parts are cos(nθ) and the imaginary parts are sin(nθ)

how to change cosⁿx/sinⁿx into sum of multiple angles

• express trig function in exponential form

• let z=e^iθ such that cosⁿ(x) = ½[z+(1/z)] and sin(x)=(1/2i)[z-(1/z)]

• expand this using binomial expansion

• gather inverse terms together

• zⁿ±(1/zⁿ)= 2cos(nθ)/2sin(nθ) - de Moivre

• done!

integral of cosnθ

(1/n)[sin(nθ)]

integral of sin(nθ)

(-1/n)cosnθ