CALC DERIVATIVE RULES AND IDENTITIES

Requirements for a limit to exist

1. Left-hand limit exists

2. Right-hand limit exists

3. Both limits are equal

If any 1 of these conditions fail, limit does not exist

Cases where limit does not exist

1. Jump discontinuity - the two one-sided limits are not equal

2. Infinite discontinuity - function approaches a vertical asymptote and either goes to infinity or negative infinity

derivative of arcsin

1/√(1-x²)

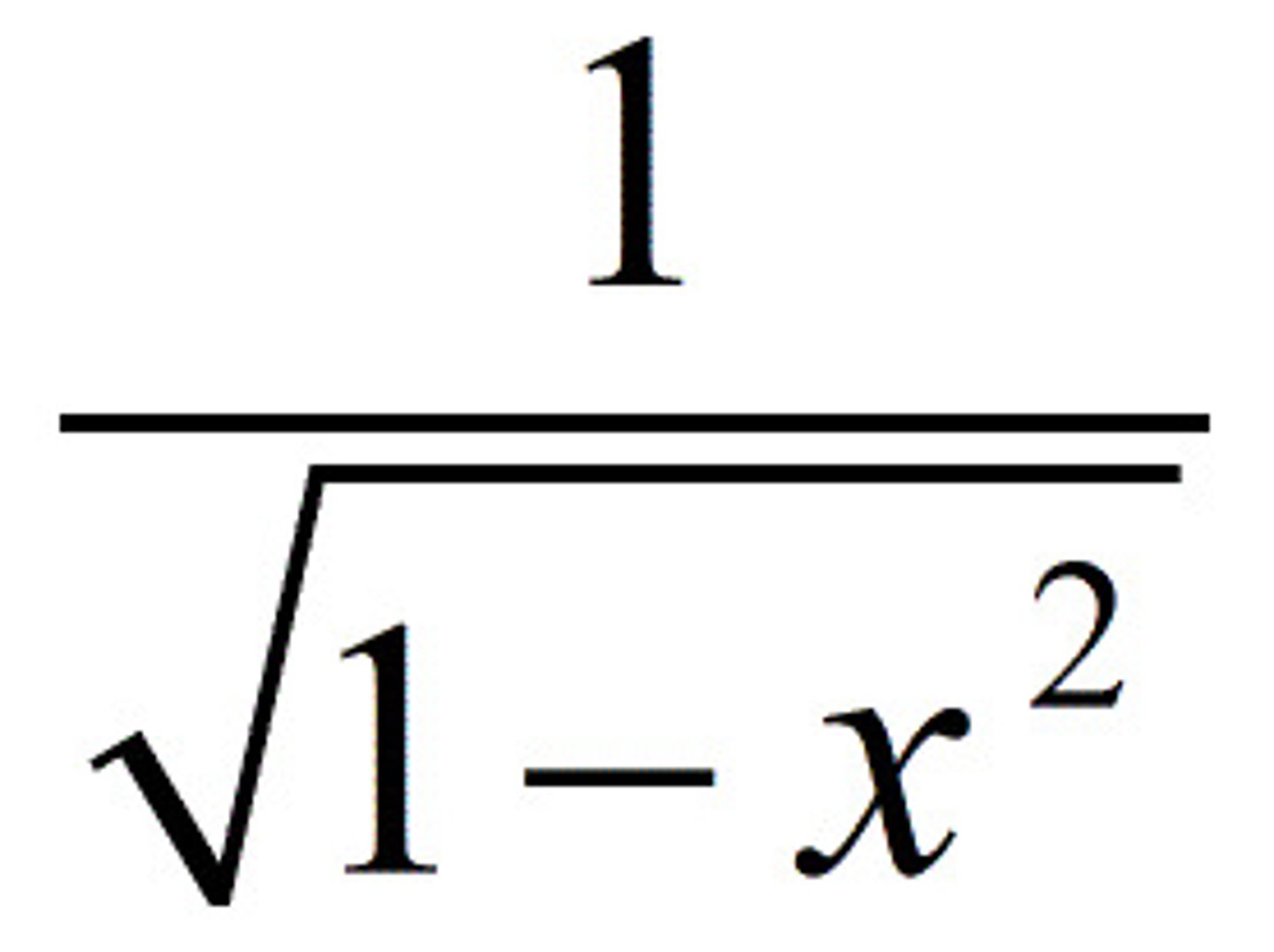
d/dx cos⁻¹(x) aka d/dx arccos(x)

-1/√(1-x²)

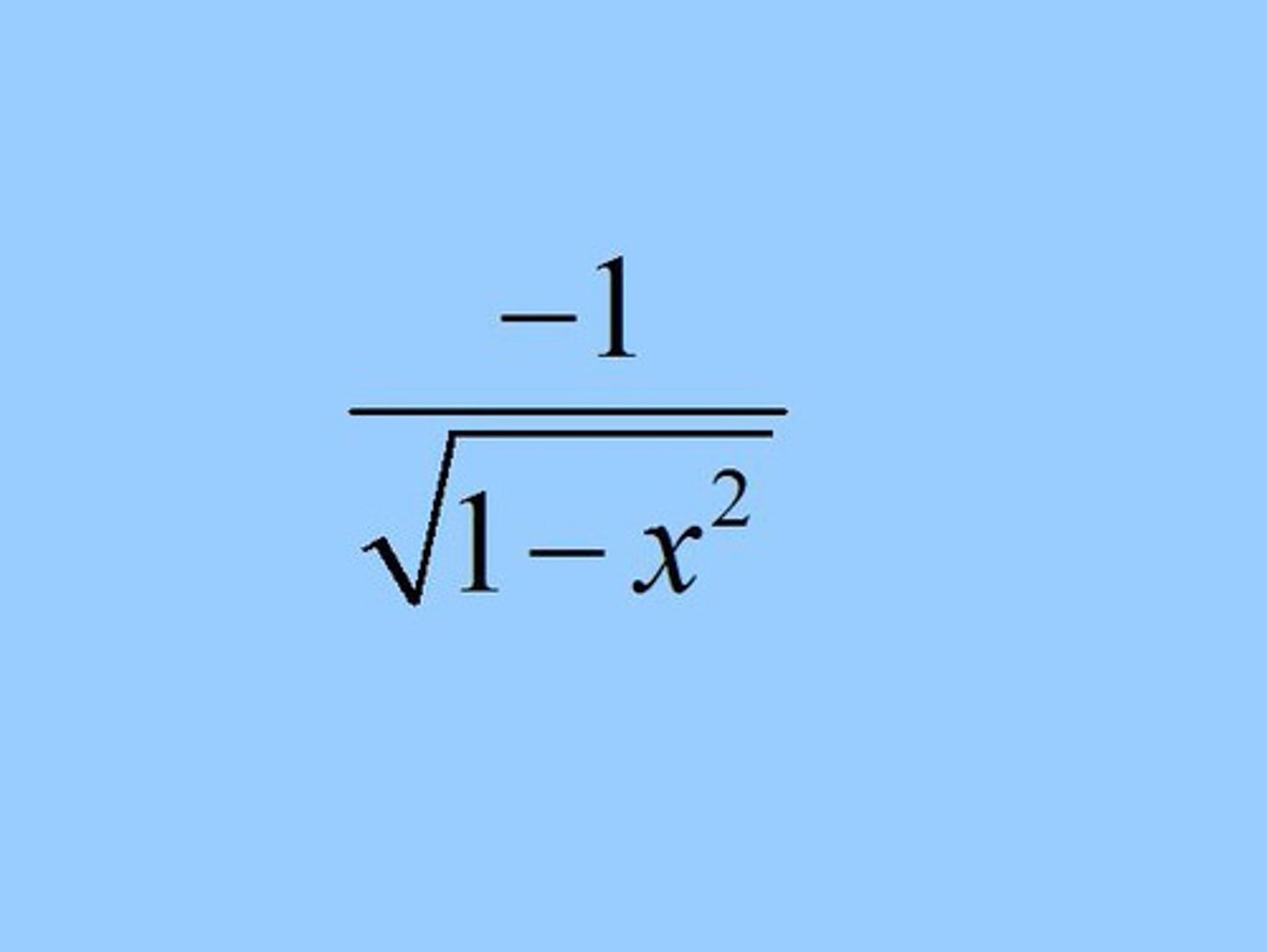
derivative of arctan

1/(1+x²)

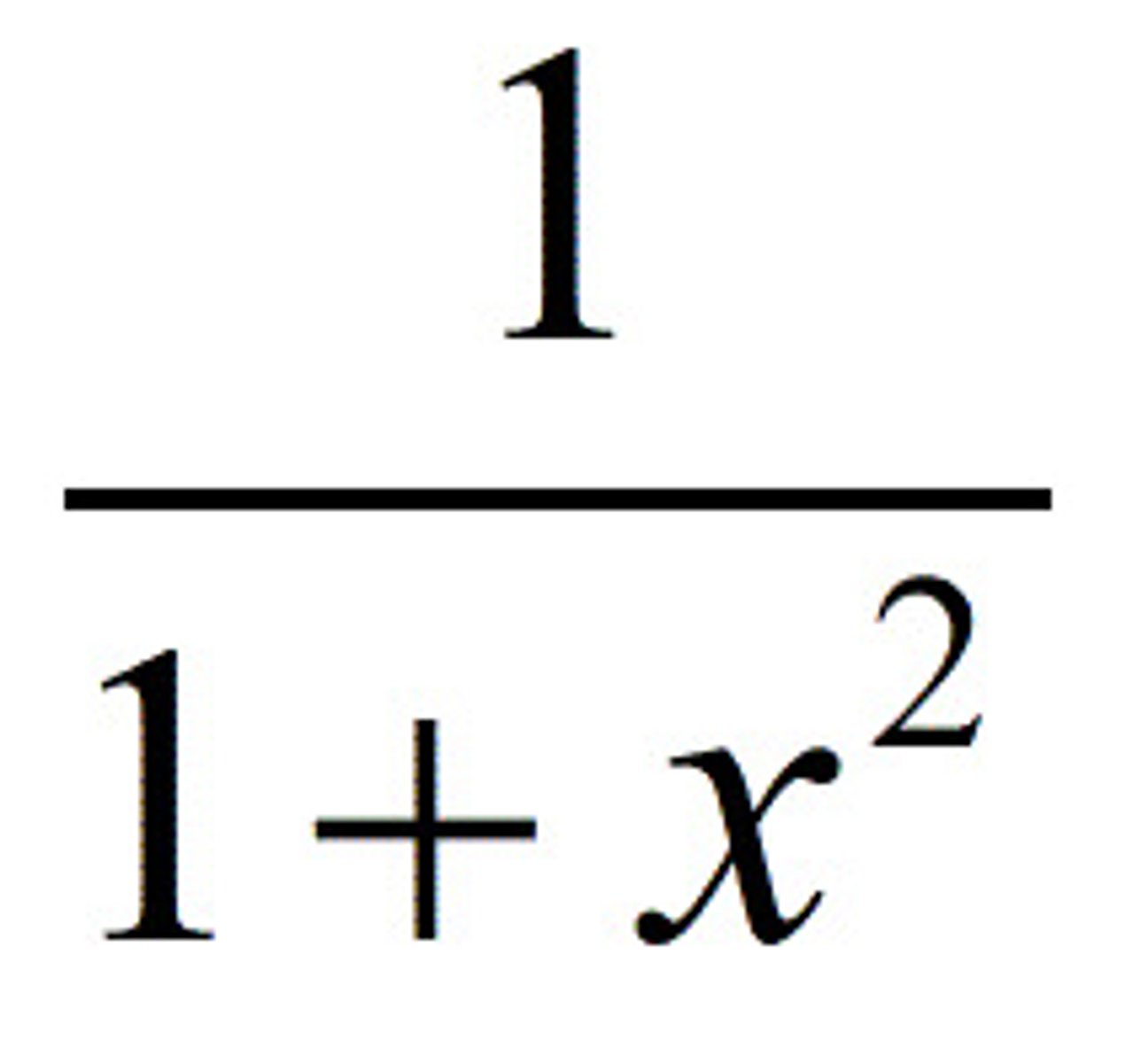
derivative of arc csc

-1/(|x| √(x²-1))

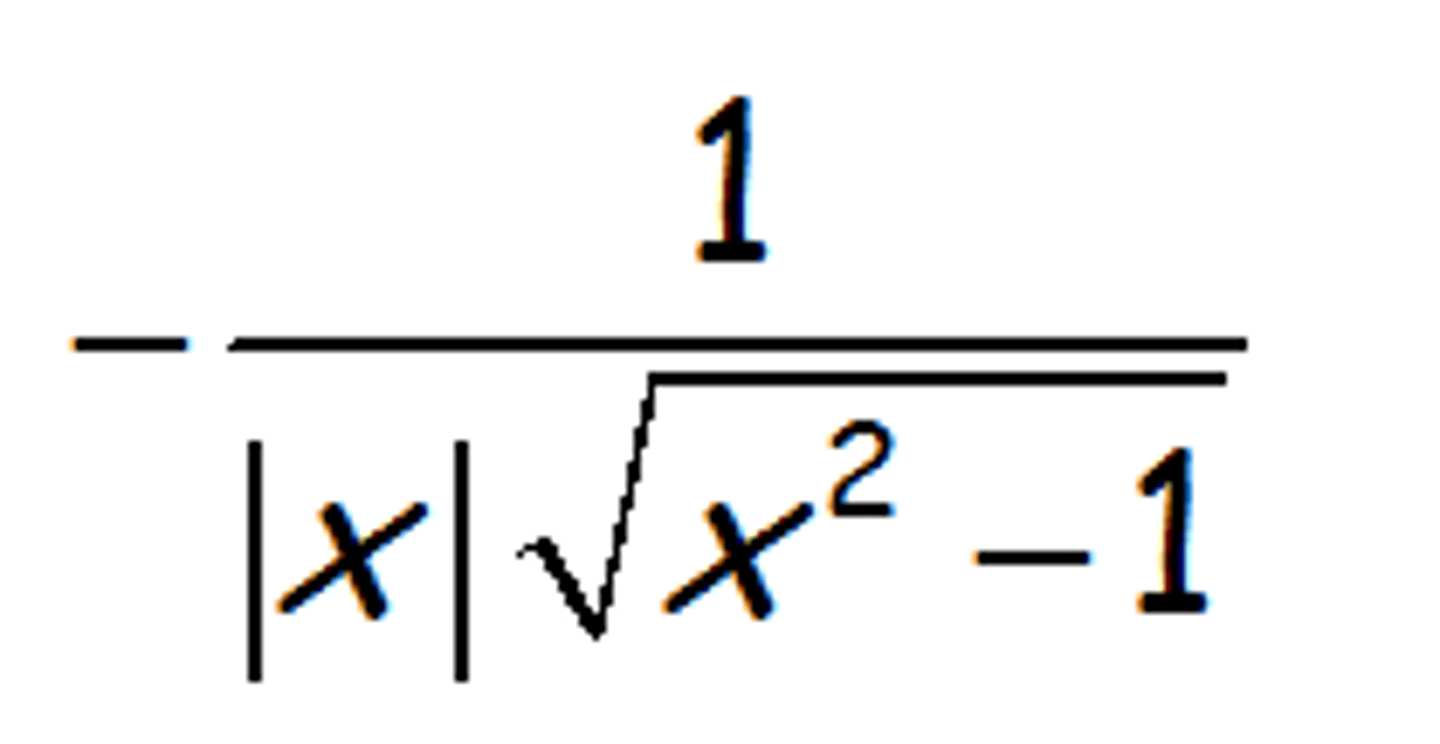
derivative of arc secant

1/(|x| √(x²-1))

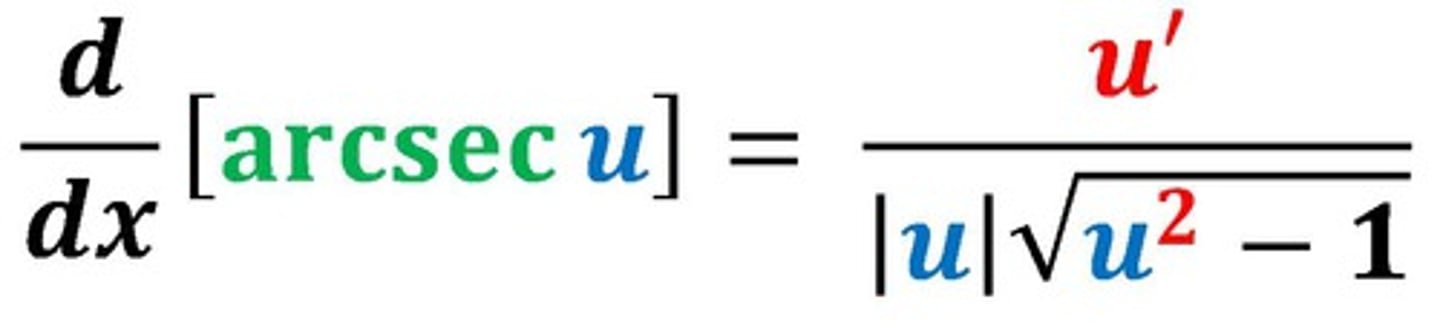
derivative of arc cot

-1/(1+x²)

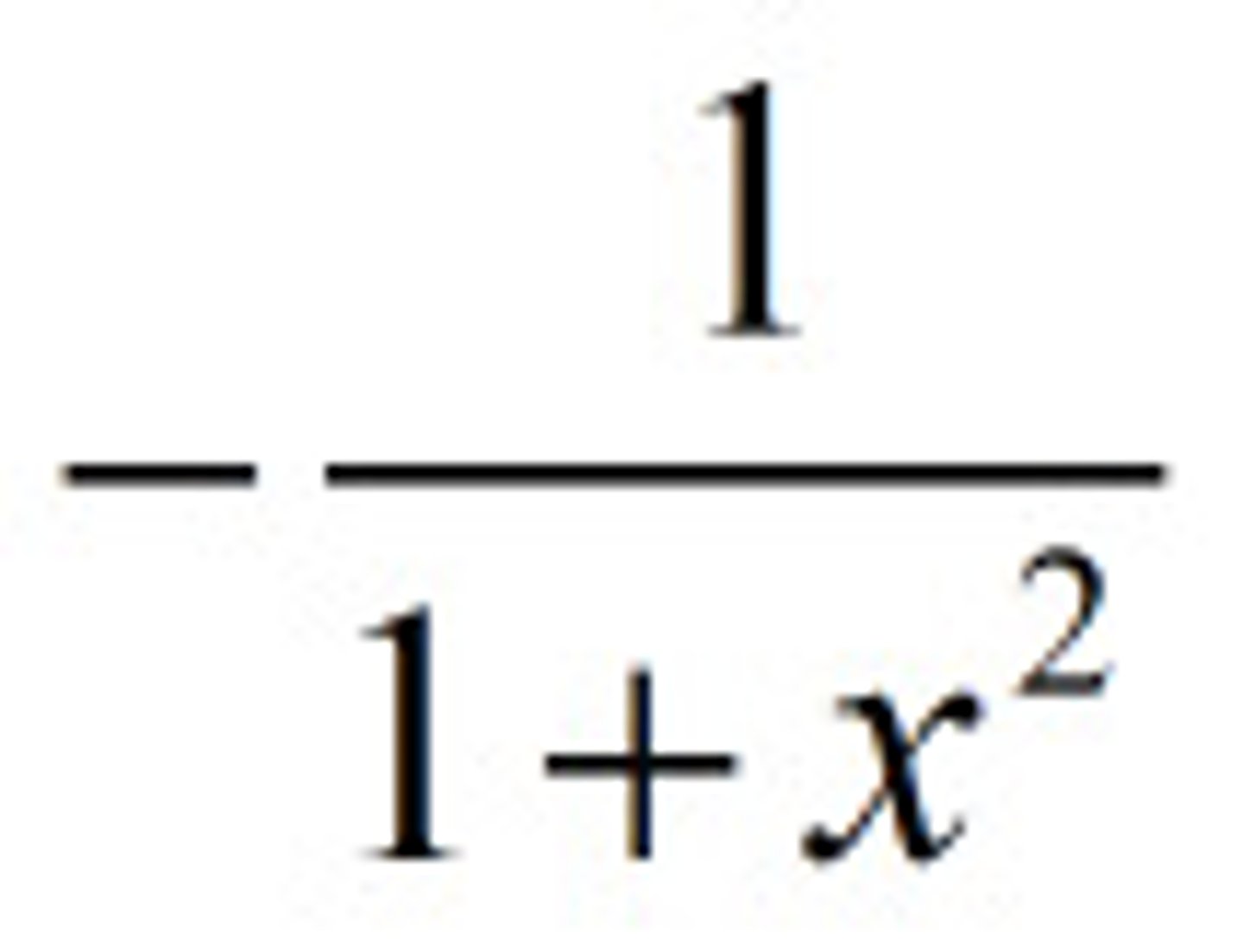
d/dx (sin x)

cos x

d/dx (cos x)

- sin x

d/dx (tan x)

sec squared of x

d/dx (csc x)

- csc x * cot x

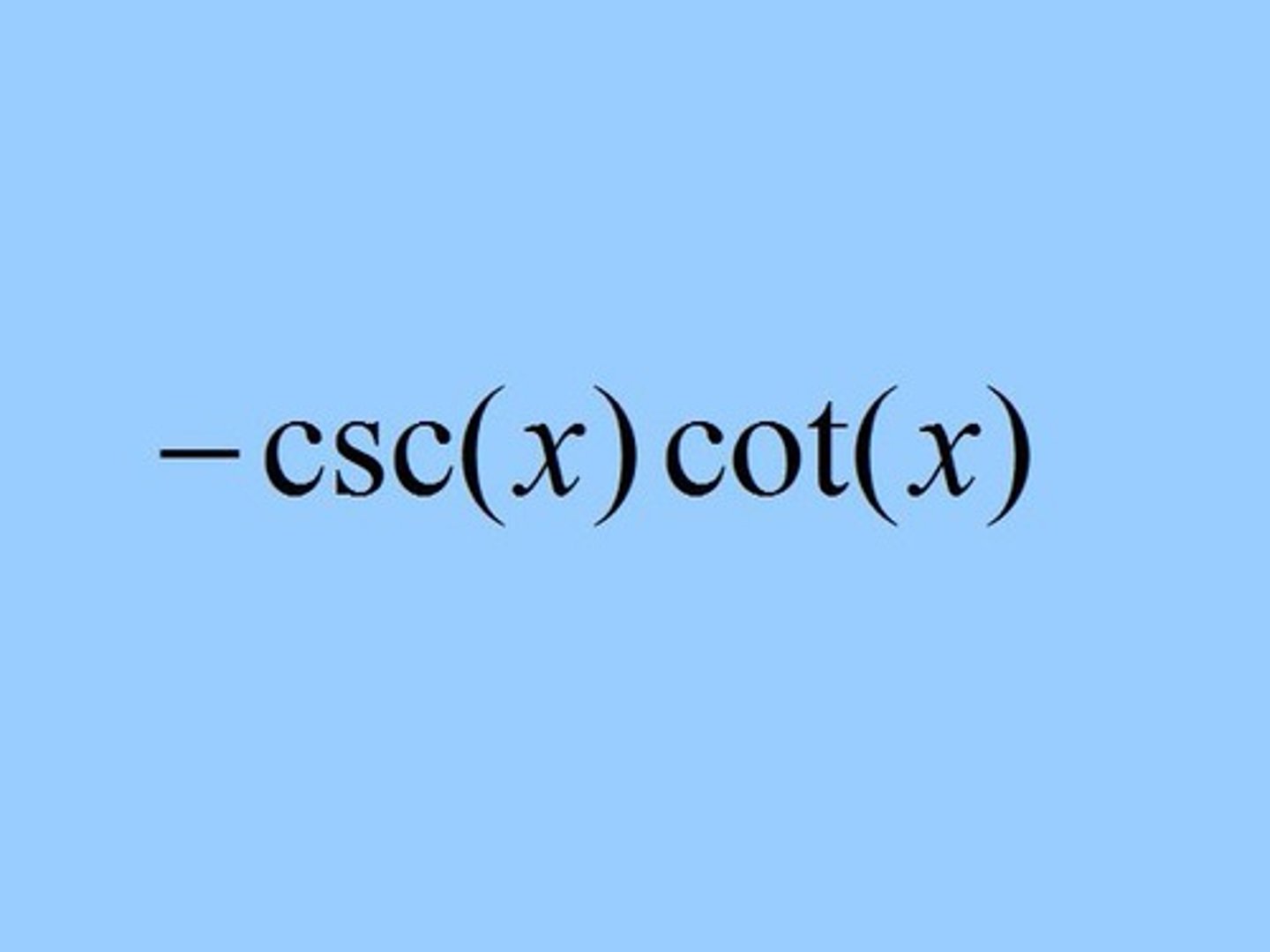
d/dx (sec x)

sec x * tan x

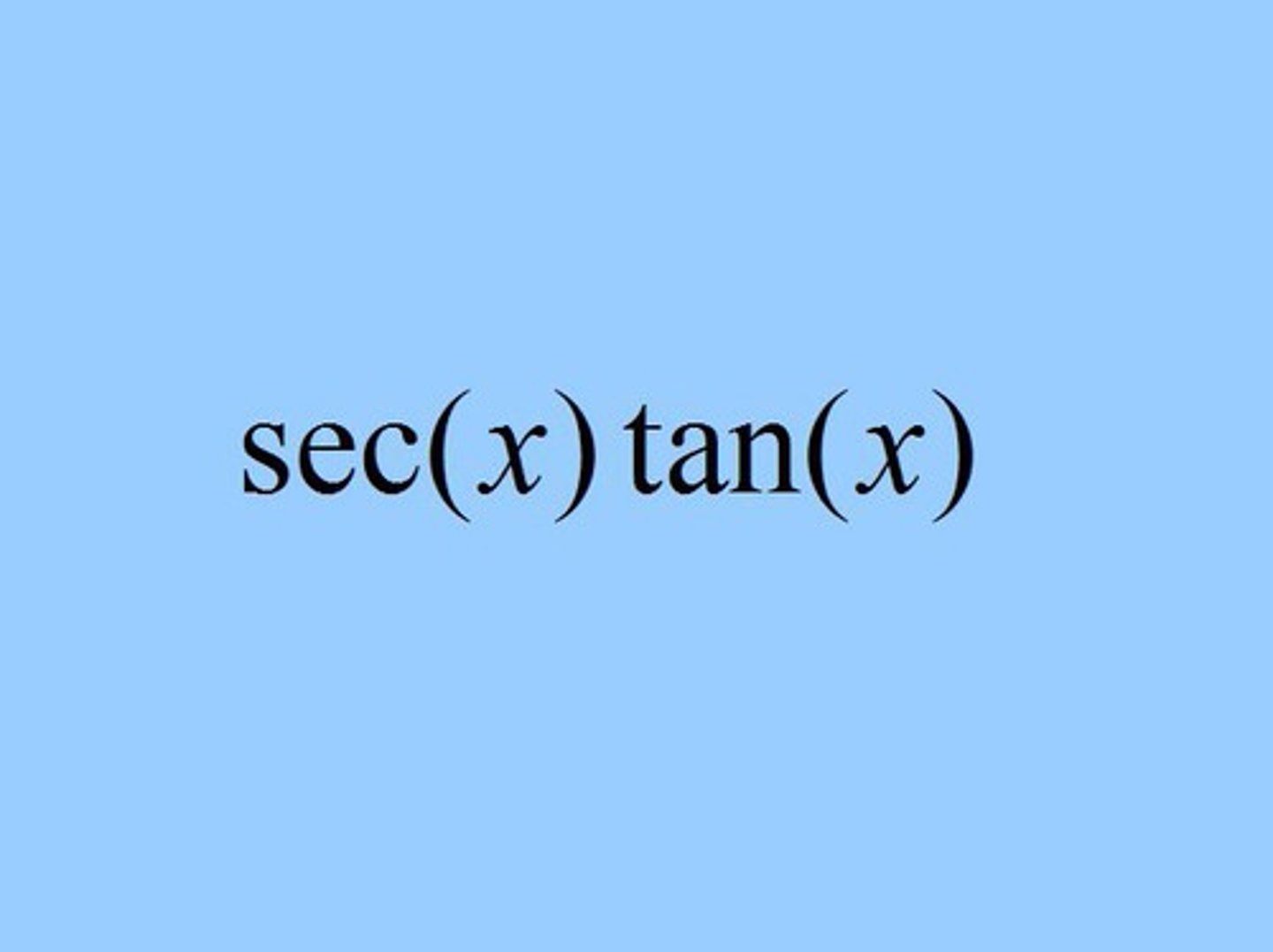
d/dx (cot x)

- csc squared of x

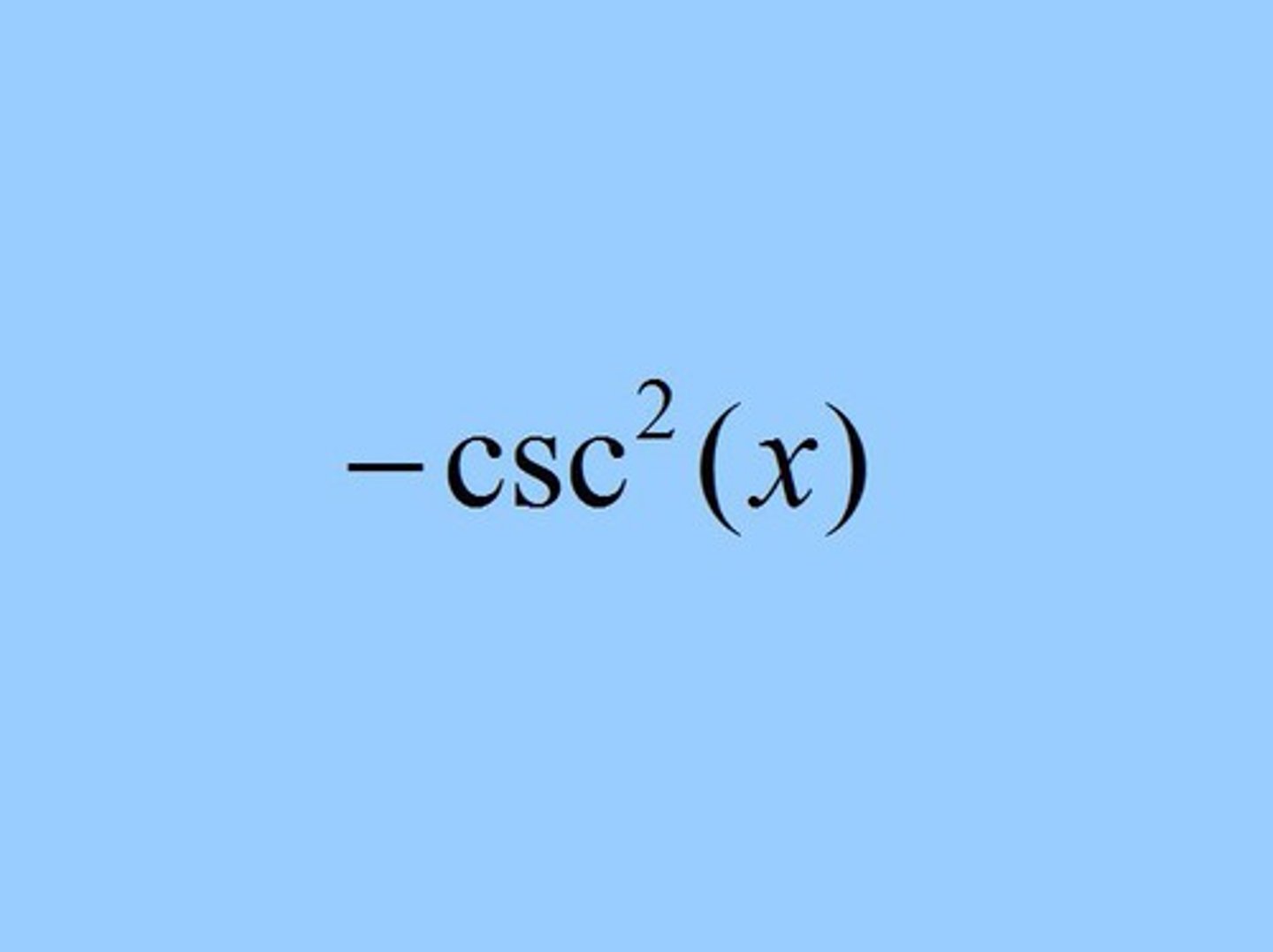
y = f(x) * g(x) (Product Rule)

y' = f'(x) * g(x) + g'(x) * f(x)

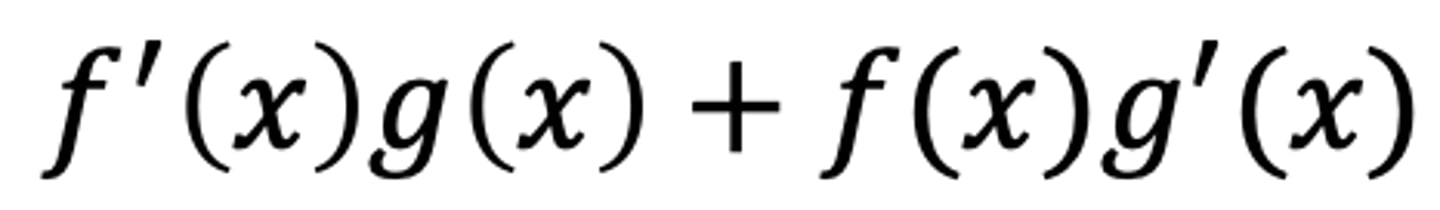
y = f(x) / g(x) (Quotient Rule)

y' = f'(x)* g(x) - g'(x) * F(x) / [g(x)]^2

d/dx [constant] (Constant Rule)

Derivatives of all constants are zero!

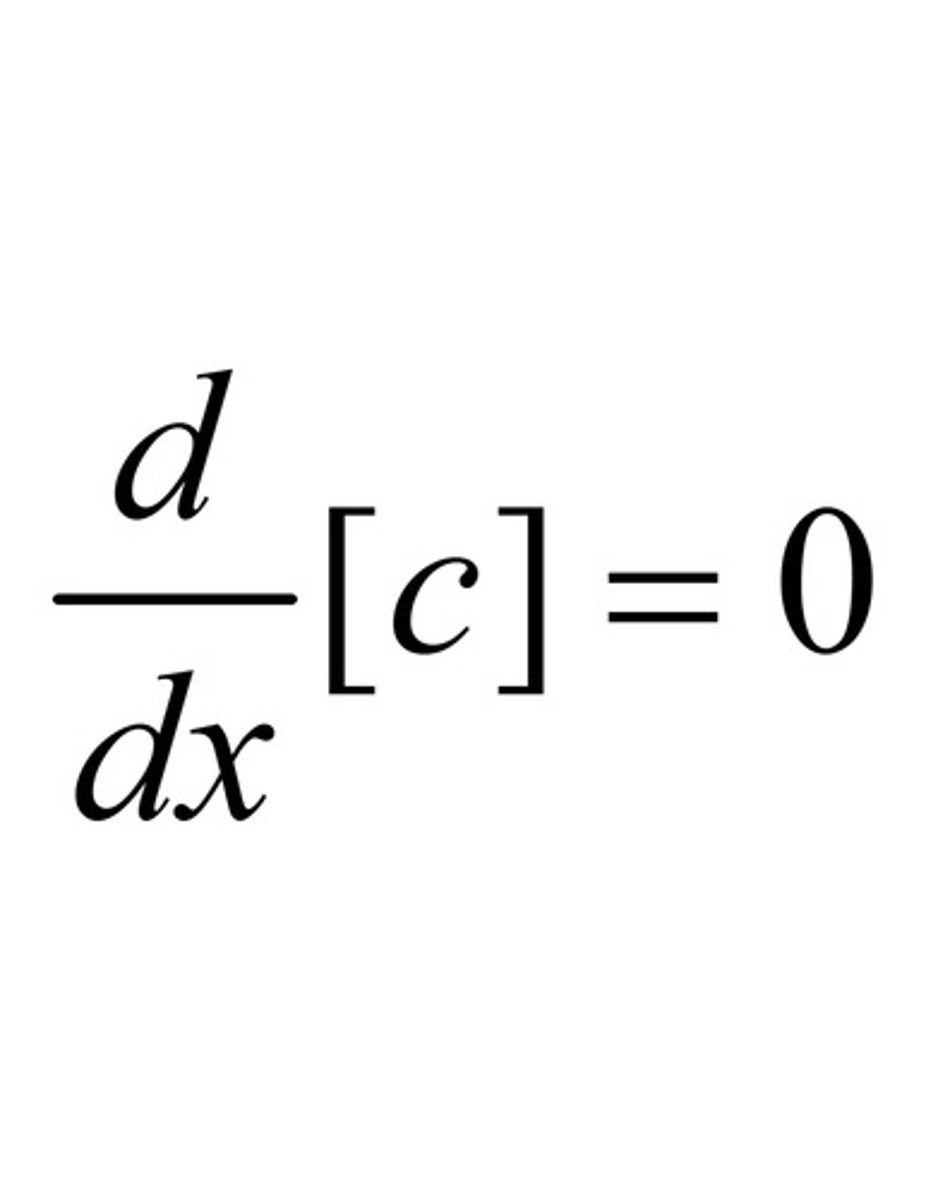
d/dx [x]

Derivative of x is 1, derivative of anything multiplied by x is just constant

e.g. d/dx [5x] = 5

d/ dx [y]

dy/dx (implicit differentiation)

sin squared of x + cos squared of x

= 1

sec ^2 of x

= 1 + tan ^2 of x

csc squared of x =

= 1 + cot ^2 of x

sin (2x)

= 2 sin x cos x

cos (2x)

= cos^2(x)- sin^2(x) = 2cos^2(x) - 1 = 1 - 2sin^2(x)

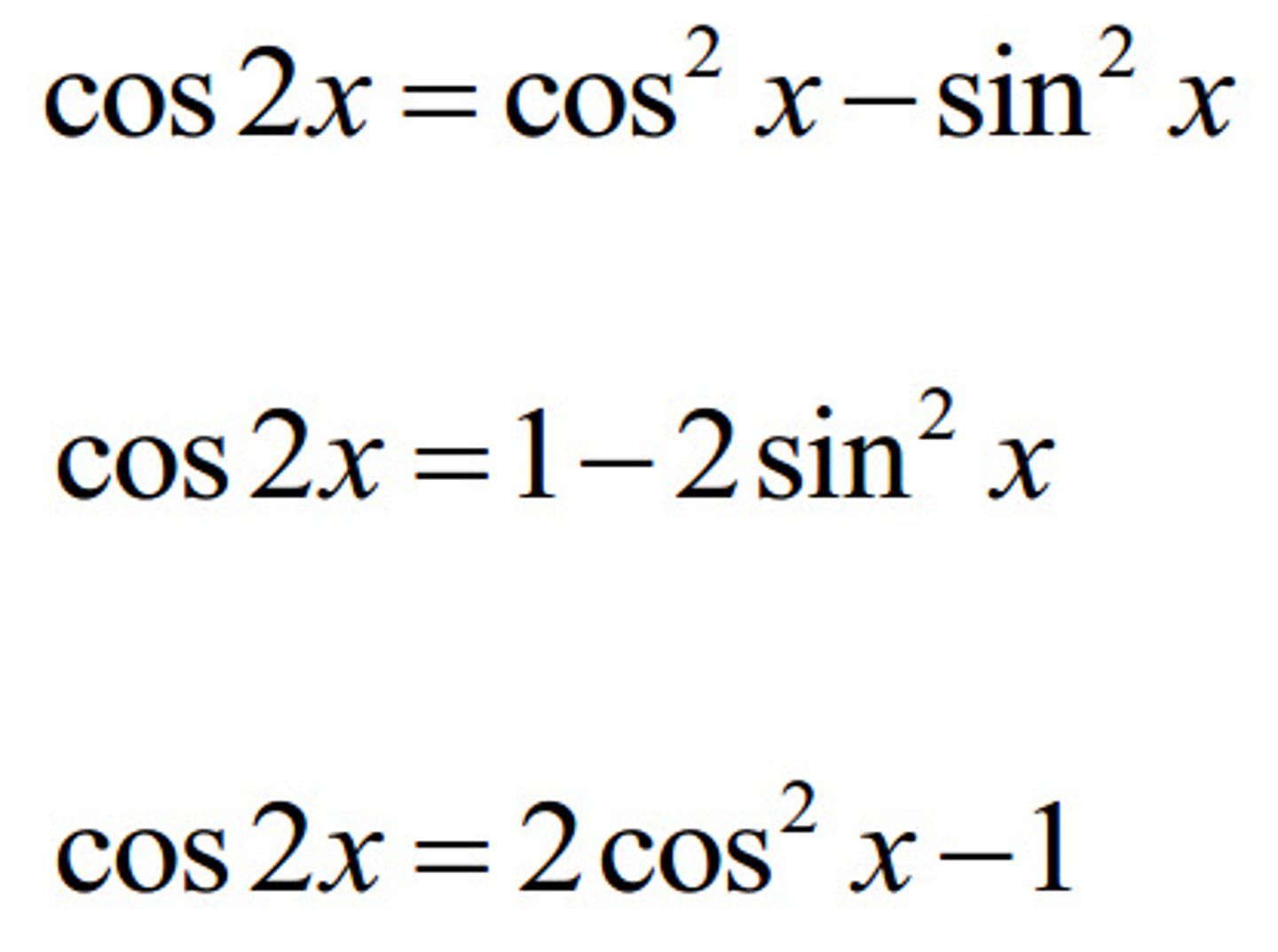
Power Rule

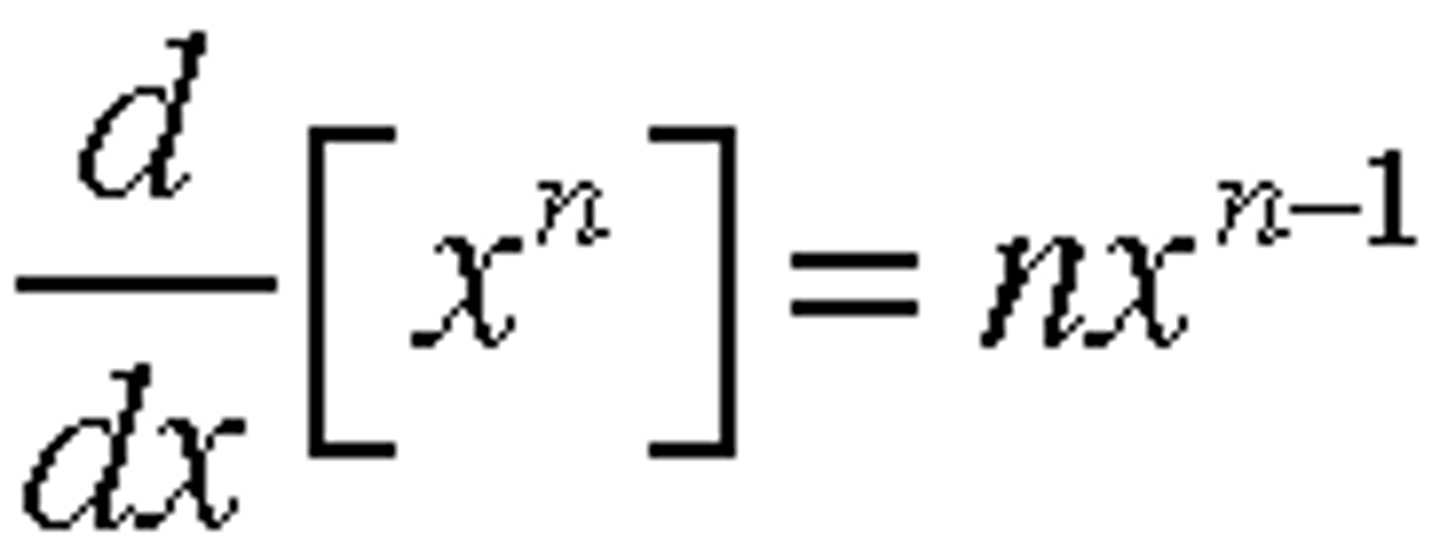
Requirements for function to be continuous

f(x) is continuous at x = a if:

1. f(a) is defined (the function has a value at a)

2. The left hand and right hand limits both exist and are equal

3. The limit is equal to the function value

Requirements for function to be continous

f(x) is continuous at x = a if:

1. f(a) is defined (function has a value at a)

2. The left hand and right hand limits exist and are equal

3. The function value is equal to the limit

Types of Discontinuities: Hole (removable)

1. Limit exists- both left and right hand limits exist and are equal

2. BUT - the function is not defined at the same value the two limits approach

3. Able to be factored and canceled out but still undefined at that one value, thus resulting in a hole

E.g. (x^2-4) / (x-2) has a hole at x = 2, but it can be canceled out

Types of Discontinuities: Infinite (non-removable)

1. Function is undefined at a certain point - denominator = 0

2. Limit does not exist for the function because some combo of positive and negative infinity is reached on either side's limit

E.g. 1 / (x-3) - x = 3 is a infinite discontinuity

it's not a hole since u can't cancel it out

as x approaches 3 from both sides you go to (+) or (-) infinity

So the function is undefiend at 3 bc denominator = 0 at that point, AND limit does not exist at that point

Types of Discontinuities: Jump (non-removable)

1. Function is defined at point

2. Left hand and right hand limit both exist

3. Two side limits do not equal each other