AP Calculus AB/BC Formula Sheet

AP Calculus AB/BC Formula Sheet

Definition of a Limit

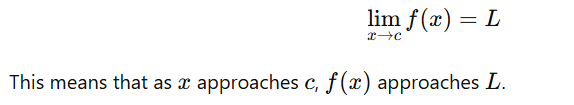
Properties of Limits

Includes limit laws such as the sum, difference, product, and quotient of limits.

Derivative Definition

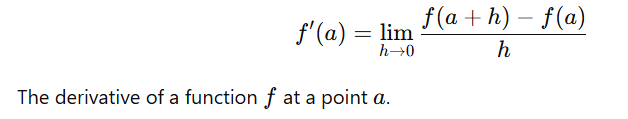
Power Rule

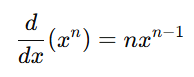
Product Rule

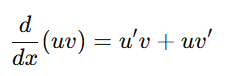
Quotient Rule

\frac{d}{dx}\left(\frac{u}{v}\right) = \frac{u'v - uv'}{v^2}.

Chain Rule

\frac{d}{dx}(f(g(x))) = f'(g(x))g'(x).

Definite Integral

The definite integral of (f) from (a) to (b) is given by: \int_a^b f(x) , dx = F(b) - F(a) where (F) is an antiderivative of (f).

Fundamental Theorem of Calculus Part 1

If (F) is an antiderivative of (f) on ([a, b]), then: \int_a^b f(x) , dx = F(b) - F(a).

Fundamental Theorem of Calculus Part 2

If (f) is continuous on ([a, b]), then (F(x) = \int_a^x f(t) , dt) is differentiable and (F'(x) = f(x)).

Critical Points

Points where (f'(x) = 0) or (f'(x)) is undefined.

First Derivative Test

Used to determine local extrema by analyzing the sign of (f'(x)).

Second Derivative Test

If (f''(x) > 0), (f) is concave up; if (f''(x) < 0), (f) is concave down.

Area Under a Curve

The area between the curve (y = f(x)) and the x-axis from (a) to (b) is given by \int_a^b f(x) , dx.

Volume of Revolution - Disk Method

V = \pi \int_a^b [f(x)]^2 , dx.

Volume of Revolution - Washer Method

V = \pi \int_a^b \left([R(x)]^2 - [r(x)]^2\right) , dx.

Convergence Tests (BC Only)

Includes tests such as the Ratio Test, Root Test, and Integral Test.

Taylor Series

The Taylor series of (f(x)) centered at (a) is given by: f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \cdots.

Maclaurin Series

A special case of the Taylor series where (a = 0).

Parametric Equations Derivative

The derivative can be expressed as: \frac{dy}{dx} = \frac{dy/dt}{dx/dt} = \frac{g'(t)}{f'(t)}.

Arc Length of Parametric Curve

L = \int_a^b \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} , dt.

Polar Coordinates Definition

In polar coordinates, a point is represented as ((r, \theta)), where (r) is the distance from the origin and (\theta) is the angle.

Conversion to Cartesian Coordinates

x = r \cos(\theta), \quad y = r \sin(\theta).

Derivative in Polar Coordinates

\frac{dy}{dx} = \frac{\frac{dy}{d\theta}}{\frac{dx}{d\theta}} = \frac{r' \sin(\theta) + r \cos(\theta)}{r' \cos(\theta) - r \sin(\theta)}.

Area in Polar Coordinates

A = \frac{1}{2} \int_a^b [f(\theta)]^2 , d\theta.

Separation of Variables

To solve a differential equation of the form \frac{dy}{dx} = g(x)h(y), separate the variables: \frac{1}{h(y)} , dy = g(x) , dx.

First-Order Linear Differential Equations

Expressed as: \frac{dy}{dx} + P(x)y = Q(x); with integrating factor e^{\int P(x) , dx}.

Mean Value Theorem

If (f) is continuous on ([a, b]) and differentiable on ((a, b)), there exists at least one (c \in (a, b)) such that: f'(c) = \frac{f(b) - f(a)}{b - a}.

L'Hôpital's Rule

If \lim_{x \to c} f(x) = 0 and \lim_{x \to c} g(x) = 0 (or both limits approach (\pm \infty)), then: \lim_{x \to c} \frac{f(x)}{g(x)} = \lim_{x \to c} \frac{f'(x)}{g'(x)}.

Integration by Parts

For integrals of the form \int u , dv: \int u , dv = uv - \