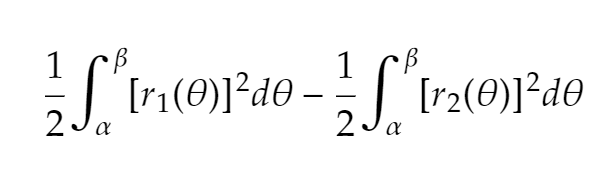Calc BC Pham Unit 11

What are parametric equations?

What are parametric equations?

Equations where the x and y axes are defined by separate functions ex:

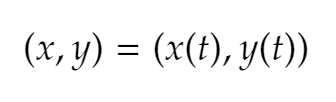
How do you graph parametric equations?

• Make a chart for the x and y functions and plot it

  • Be sure to mark the orientation of the graph, or the direction that the points go as t increases

• Use a calculator 😃

How to convert from parametric to cartesian/rectangular?

• Substitute x for t into the other equation

• Solve for y

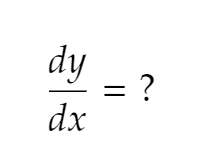
How do you take the derivative of a parametric equation?

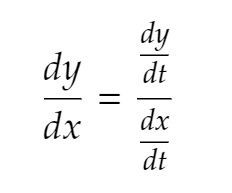
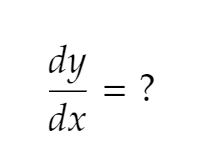
How do you take the second derivative of a parametric equation?

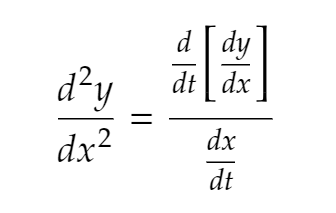
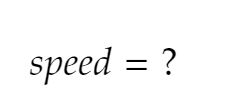
What is the equation for the speed of a parametric equation?

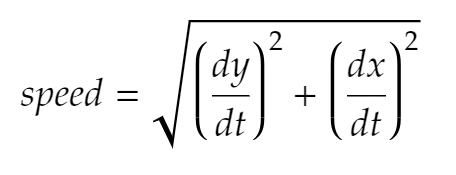
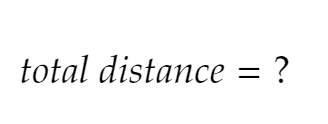
What is the equation for the total distance/arclength of a parametric equation?

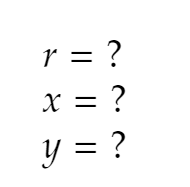
How do you convert from polar to rectangular form?

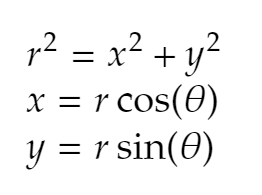
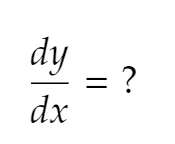
How do you find first derivatives of polar functions?

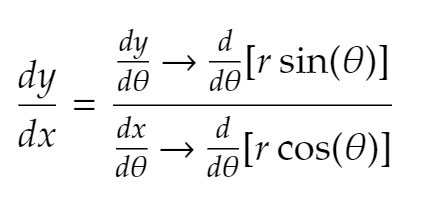
How do polar functions connect to parametrics?

Polar functions are essentially parametric functions where

• (x, y)=(rcos𝜃, rsin𝜃)

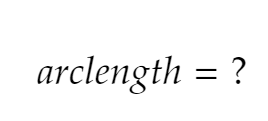
How do you find the arclength of a polar function on (𝛼, 𝛽)?

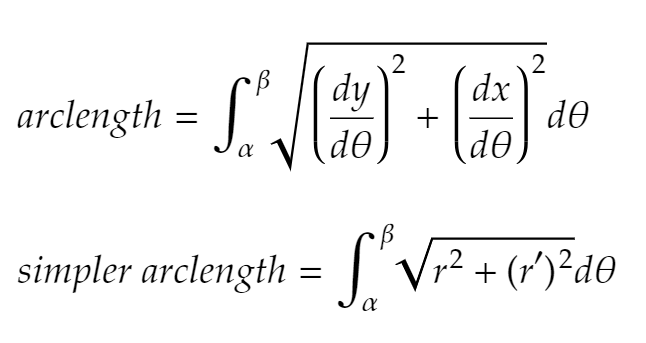
How do you find the limits of integration for polar graphs?

• Graph the polar function

• If integrating from/to the pole, substitute r=0 to find theta

• If integrating with another curve, find the intersection point by setting both equations equal and solving for theta

• If integrating to where the curve meets an axis, set r equal to whatever value it is on the axis and solve for theta

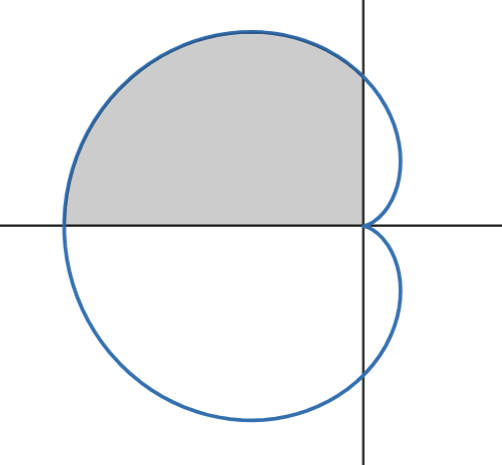
How do you find the area of a polar function on (𝛼, 𝛽)?

Note:

• Cannot integrate if graph changes sign on (𝛼, 𝛽)

  • Typically can use symmetry or separate into multiple integrals to go around this

• Integrate using the area of a sector (1/2r²𝜃)

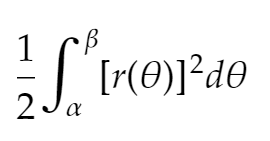
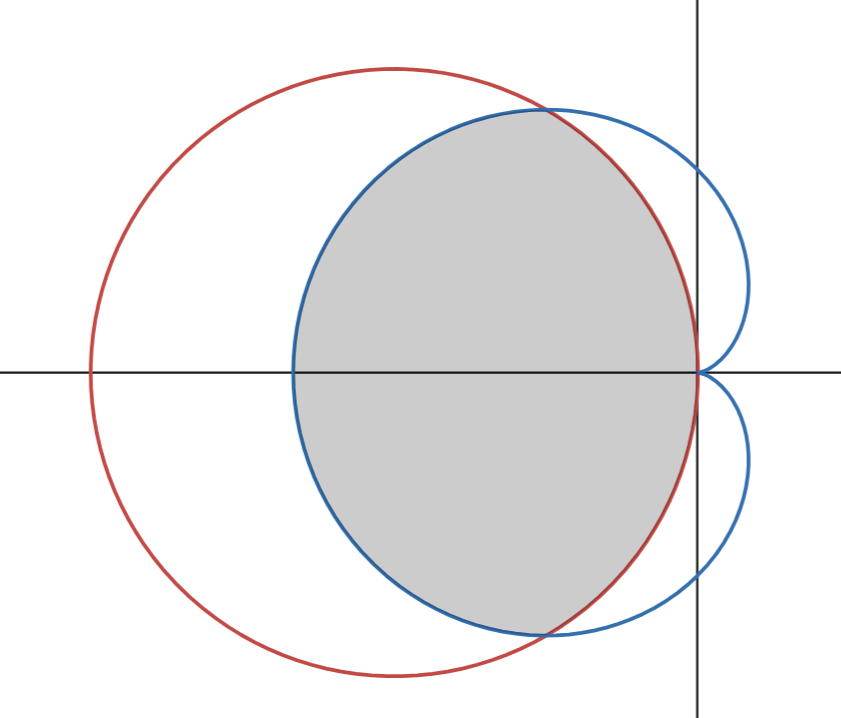
How do you find the common interior of two polar functions on (𝛼, 𝛽)?

• Find where graphs intersect (x)

• Integrate first function from 𝛼 to the intersection point

• Integrate second function from intersection point to 𝛽

• Add the two resulting integrals

• Use symmetry if necessary

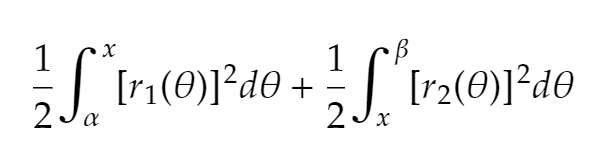
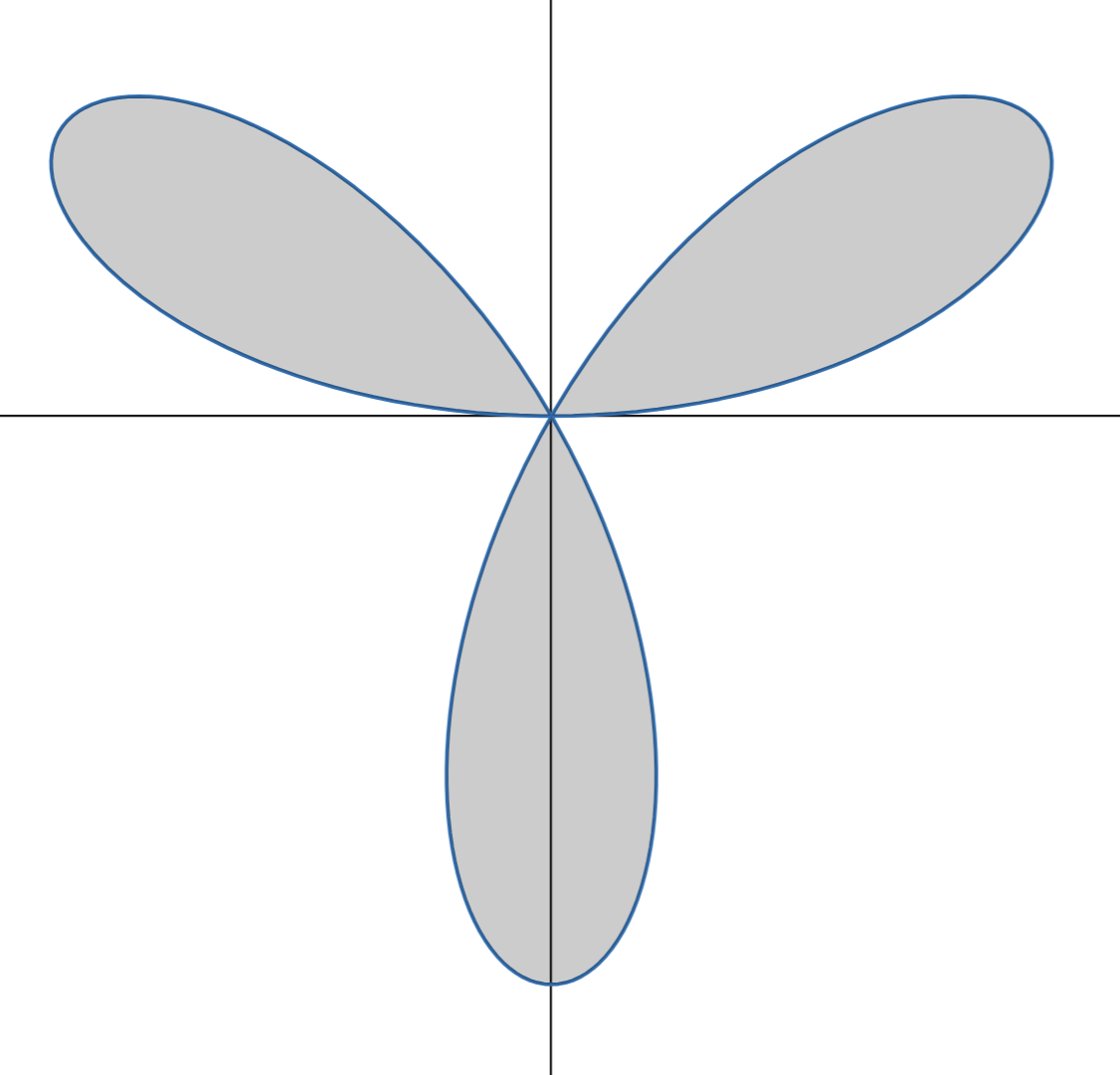
How do you find the area of a polar graph that goes through the origin?

• Find where graph intersects the origin (r=0)

• Integrate between any two consecutive intersection points

  • Must be consecutive or area will be wrong

• Use symmetry if necessary

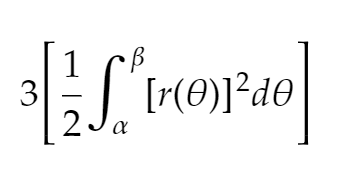
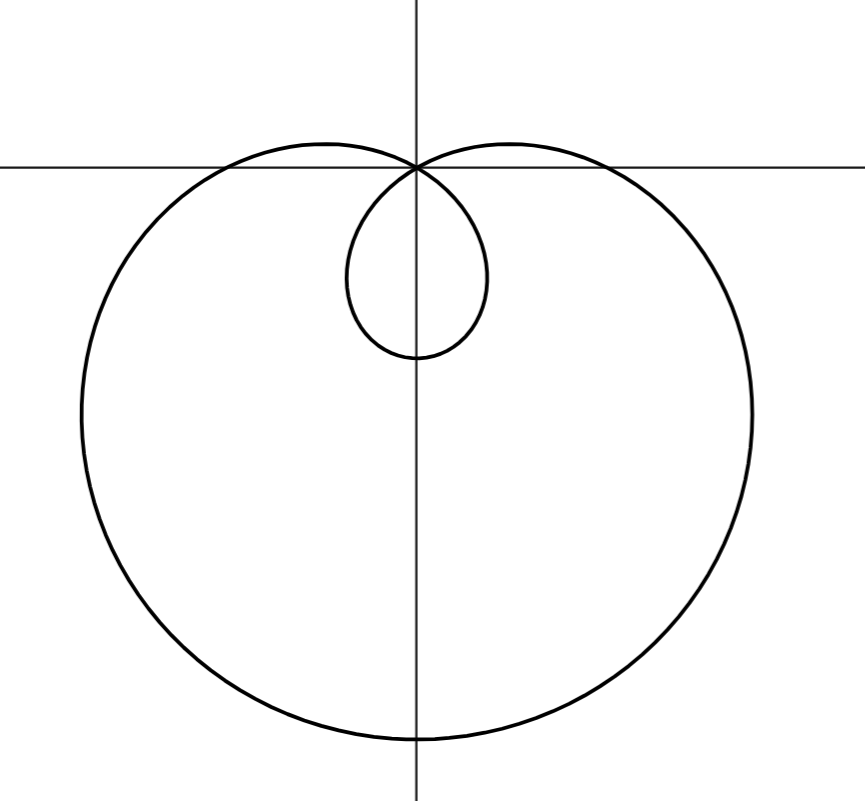
How do you find the area of a polar graph that has inner and outer loops?

• Find the bounds where the inner/outer loops lie

• Integrate outer loop

• Integrate inner loop

• Subtract area of inner loop from outer loop

• Use symmetry if necessary

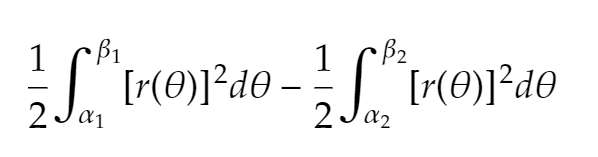
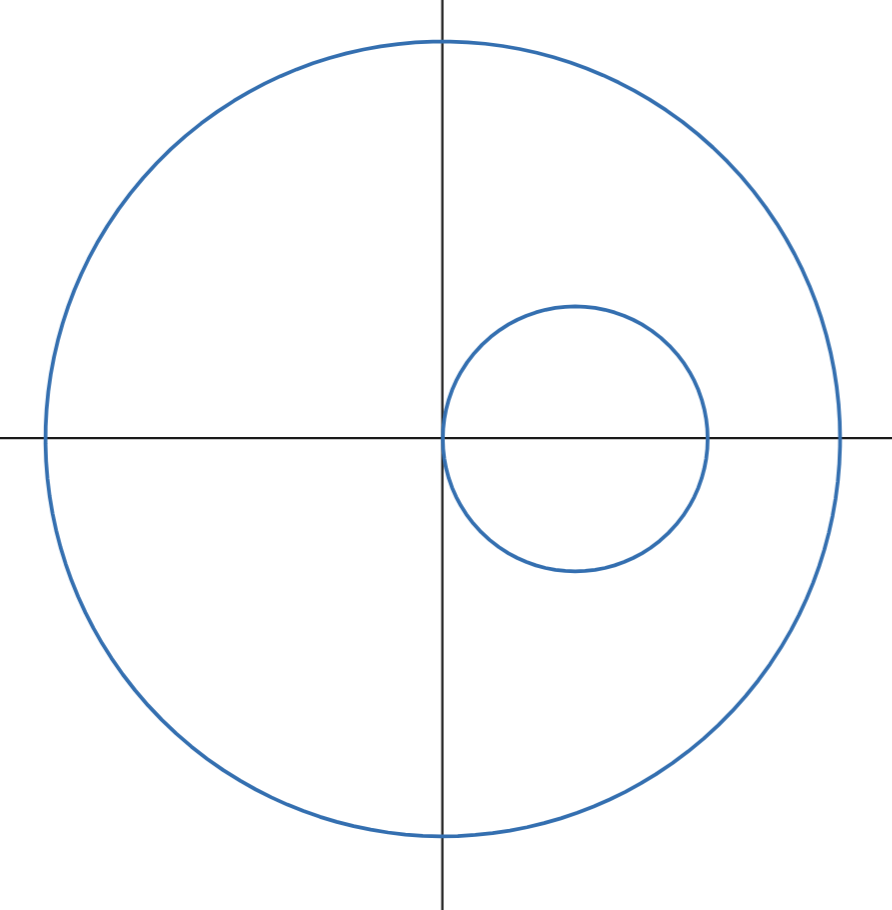
How do you find the area of a polar graph with an enclosed curve?

• Integrate outside curve

• Integrate inside curve

• Subtract area of inner curve from area of outer curve

• Use symmetry if necessary