Thẻ ghi nhớ: Công thức tính nhanh toán | Quizlet

Định lý hàm số cosin

a² = b² + c² - 2bc cos A

b² = a² + c² - 2ac cos B

c² = a² + b² - 2ab cos C

Định lý hàm số sin

a / sin A = b / sin B = c / sin C = 2R

Công thức độ dài trung tuyến

ma = √[(b² + c²) / 2 - a²/4]

mb = √[(a² + c²) / 2 - b²/4]

mc = √[(a² + b²) / 2 - c²/4]

Công thức tính diện tích tam giác

S = 1/2 a ha = 1/2 b hb = 1/2 c hc

S = 1/2 bc sin A = 1/2 ac sin B = 1/2 ab sin C

S = pr; S = abc / 4R

S = √[p(p - a)(p - b)(p - c)]

sin²x + cos²x

= 1

tanx

= sinx / cosx

cotx

= cosx / sinx

tanx . cotx

= 1

1 + tan²x

= 1 / cos²x

1 + cot²x

= 1 / sin²x

cos(-x)

= cosx

sin(-x)

= -sinx

tan(-x)

= -tanx

cot(-x)

= -cotx

sin(π - x)

= sinx

cos(π - x)

= -cosx

tan(π - x)

= -tanx

cot(π - x)

= -cotx

sin(π/2 - x)

= cosx

cos(π/2 - x)

= sinx

tan(π/2 - x)

= cotx

cot(π/2 - x)

= tanx

sin(x + π)

= -sinx

cos(x + π)

= -cosx

tan(x + π)

= tanx

cot(x + π)

= cotx

sin(x + π/2)

= cosx

cos(x + π/2)

= -sinx

tan(x + π/2)

= -cotx

cot(x + π/2)

= -tanx

sin(x ± y)

= sinx . cosy ± cosx . siny

cos(x ± y)

= cosx . cosy ∓ sinx . siny

tan(x ± y)

= (tanx ± tany) / (1 ∓ tanx . tany)

sin 2x

= 2 sinx . cosx

cos 2x

= cos²x - sin²x = 2 cos²x - 1 = 1 - 2 sin²x

tan 2x

= (2 tanx) / (1 - tan²x)

cos²x

= (1 + cos 2x) / 2

sin²x

= (1 - cos 2x) / 2

sin x

= (2t) / (1 + t²) t = tan(x/2)

cos x

= (1 - t²) / (1 + t²) với t = tan(x/2)

tan x

= (2t) / (1 - t²) với t = tan(x/2)

sin 3x

= 3 sinx - 4 sin³x

cos 3x

= 4 cos³x - 3 cosx

tan 3x

= (3 tanx - tan³x) / (1 - 3 tan²x)

cos³x

= (3 cosx + cos 3x) / 4

sin³x

= (3 sinx - sin 3x) / 4

Tổng n số hạng của cấp số nhân

S = u1 * (1 - q^n) / (1 - q) (với q ≠ 1)

Tổng n số hạng của cấp số cộng

S = n/2 (u1 + un)= n/2 (2u1 + (n-1)d)

Tính h trong tam giác thường

ha = 2 * √[p(p - a)(p - b)(p - c)] / a

Tính h trong tam giác đều

h = a * (√3) / 2

Tính h trong tam giác vuông

1.a.h = b.c 2.h² = b'.c' 3.1/h² = 1/b² + 1/c²

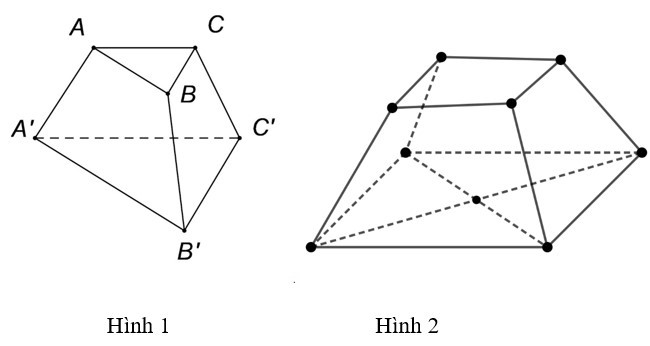
Công thức tính thể tích chóp cụt

V = (1/3) h (Sđáy lớn + √(Sđáy lớn * Sđáy nhỏ) + Sđáy nhỏ)

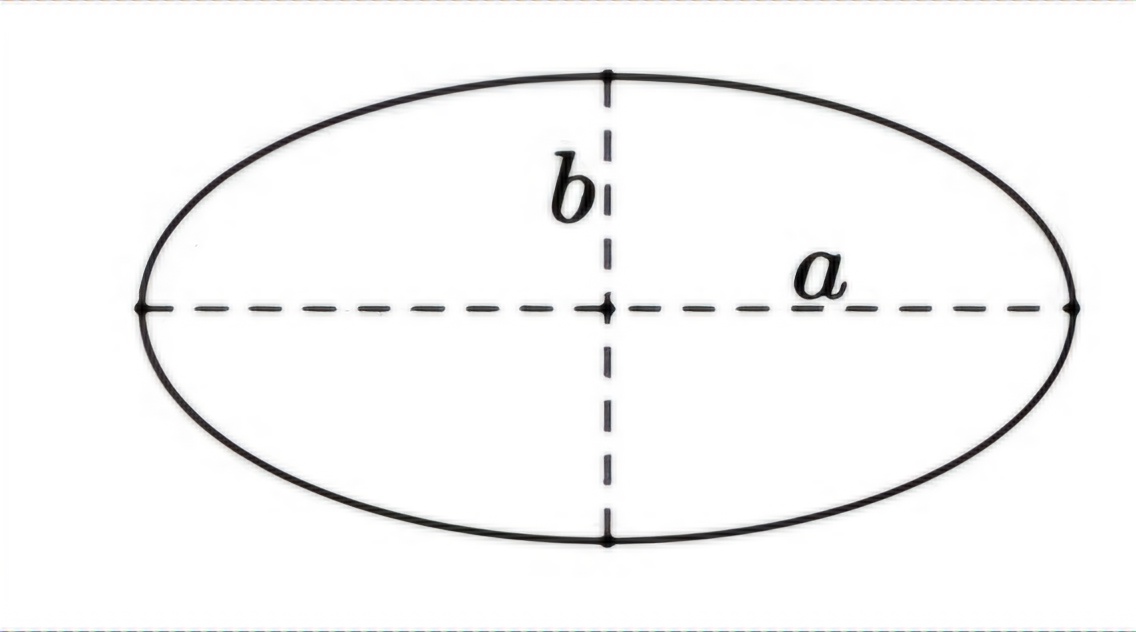
Phường trình + diện tích của Elip

1. x²/a² + y²/b² = 1 2. S = πab

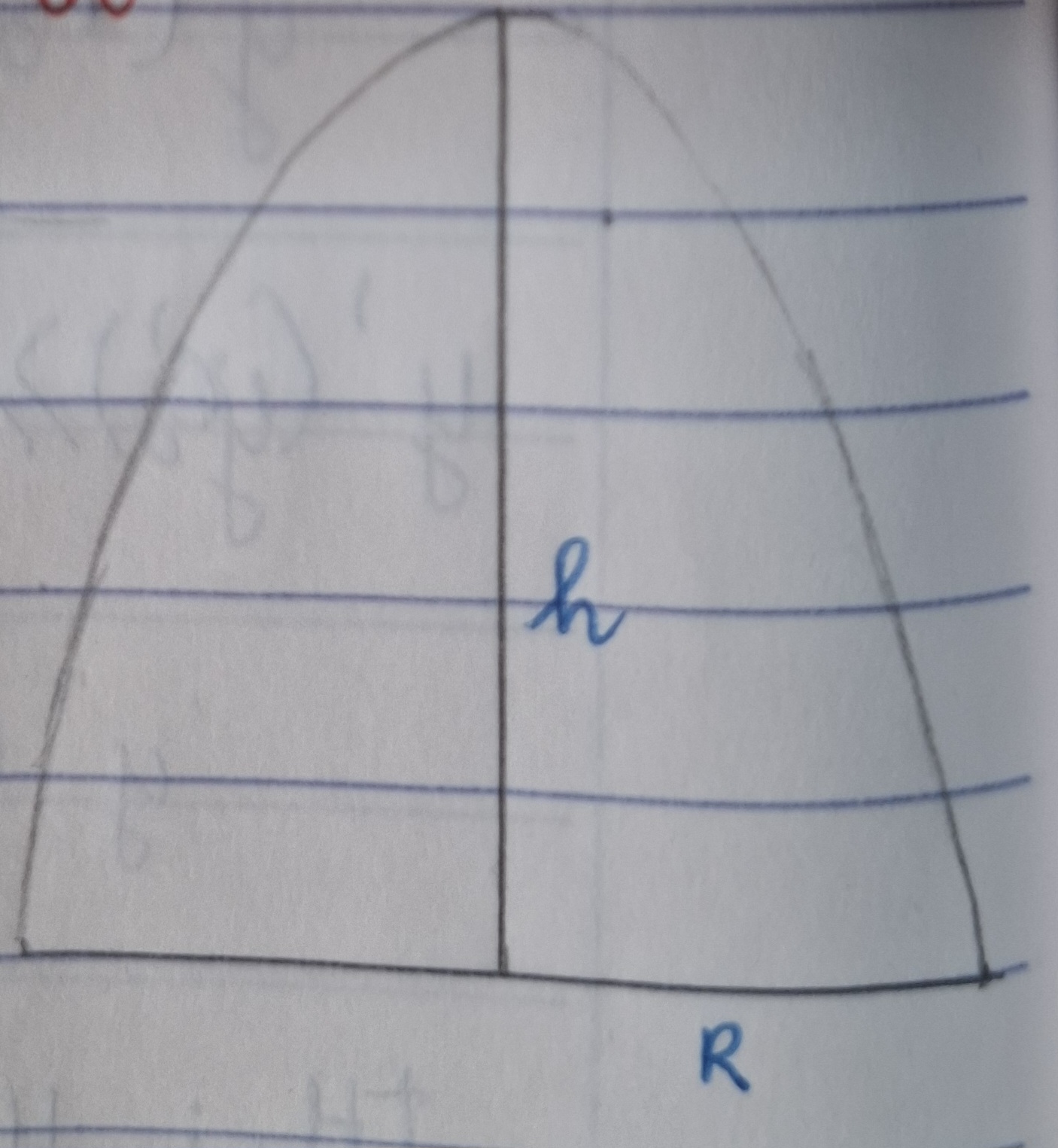
Phường trình, diện tích của Parabol

1. y = ax² + bx + c với đỉnh I (-b / 2a,-Δ / 4a) (với Δ = b² - 4ac)

2. S = 4/3Rh

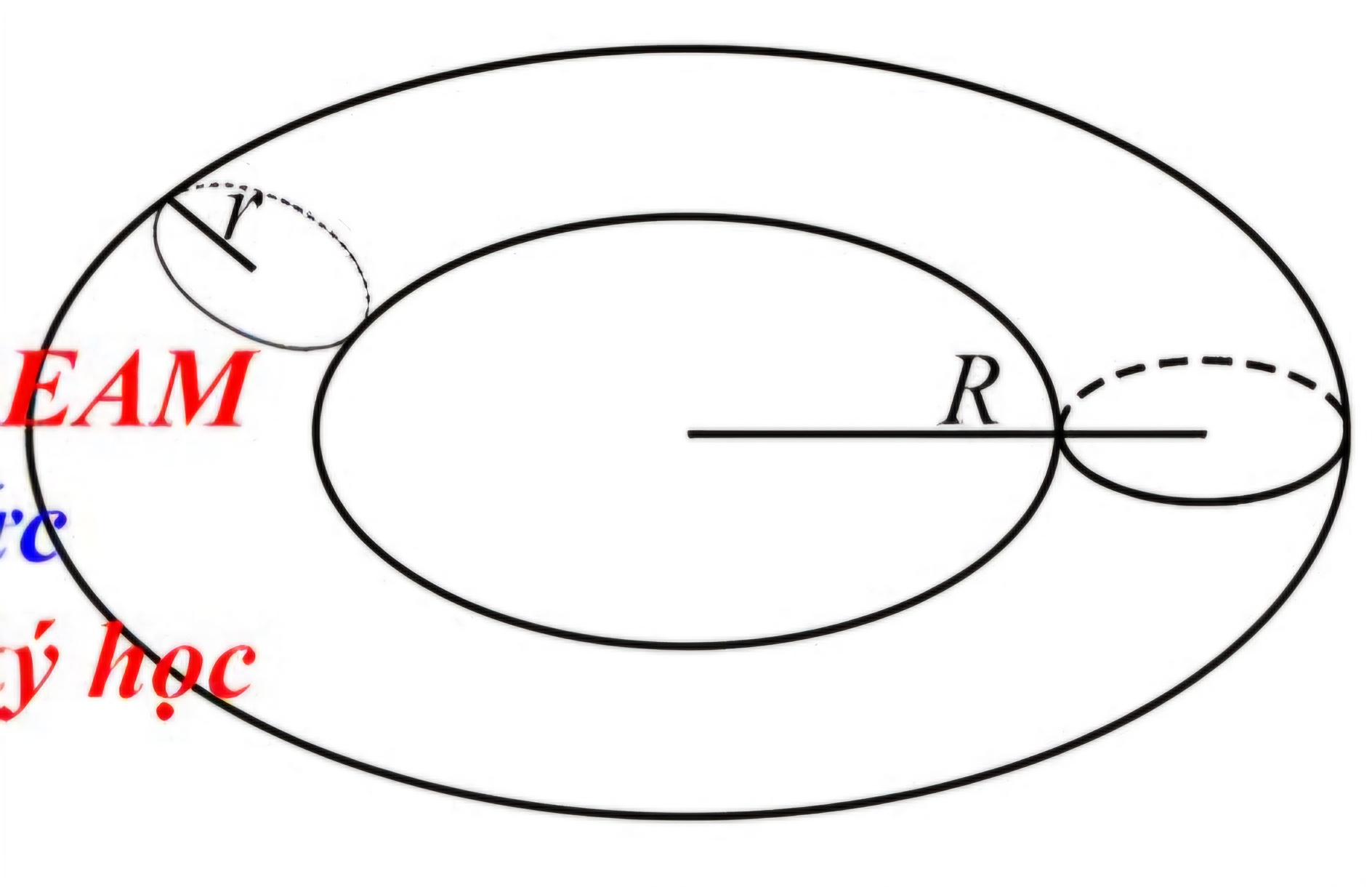
Thể tích cái phao

V = 2 π² R * r² (r: bán kinh của cái phao, R: r + bán kính khoảng trống giữa cái phao)

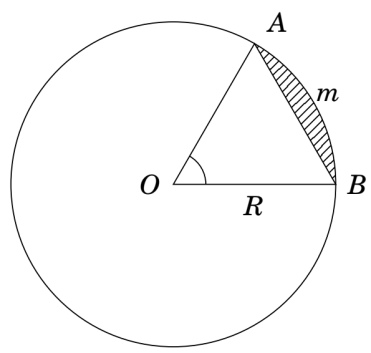
Diện tích hình viên phân

S = (R²/2) * (α - sin α)

Thể tích hình chóp

V = 1/3.Sđáy.h

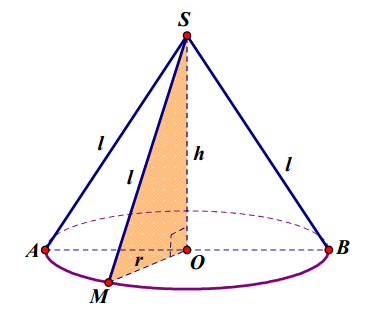
Mặt nón- Hình nón- Khối nón

1. Sxq = πRl

2. Stp = Sxq + Sđáy = πrl + πR²

3. V = (1/3)πR²h

Thể tích lăng trụ

V = Sđáy.h

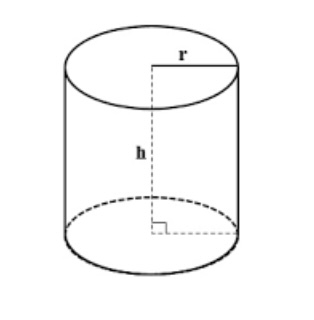
Mặt trụ- Hình trụ- Khối trụ

1. Sxq = 2πRh

2. Stp = Sxq + 2Sđáy = 2πRh + 2πR²

3. V = πR²h

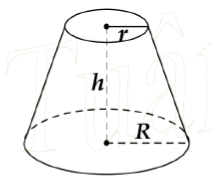
Diện tích xung quanh- Thể tích nón cụt

1. Sxq = π(R + r)l

2. V = (1/3)πh(R² + r² + Rr)

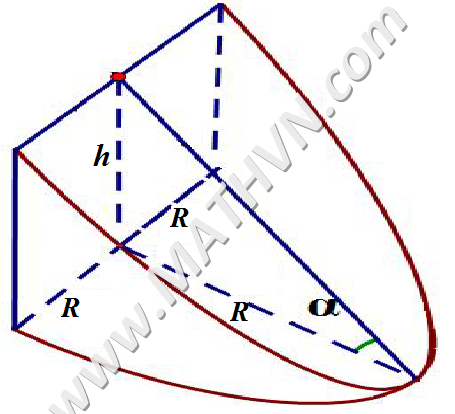
Thể tích hình nêm 1

V = (π / 2 - 2/3) R² h = (π / 2 - 2/3) R³ tan α

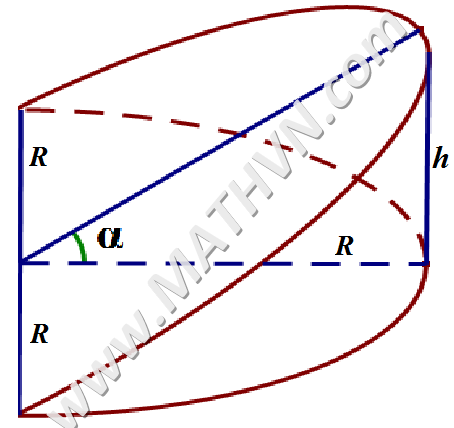
Thể tích hình nêm 2

V = (2/3) R² h = (2/3) R³ tan α

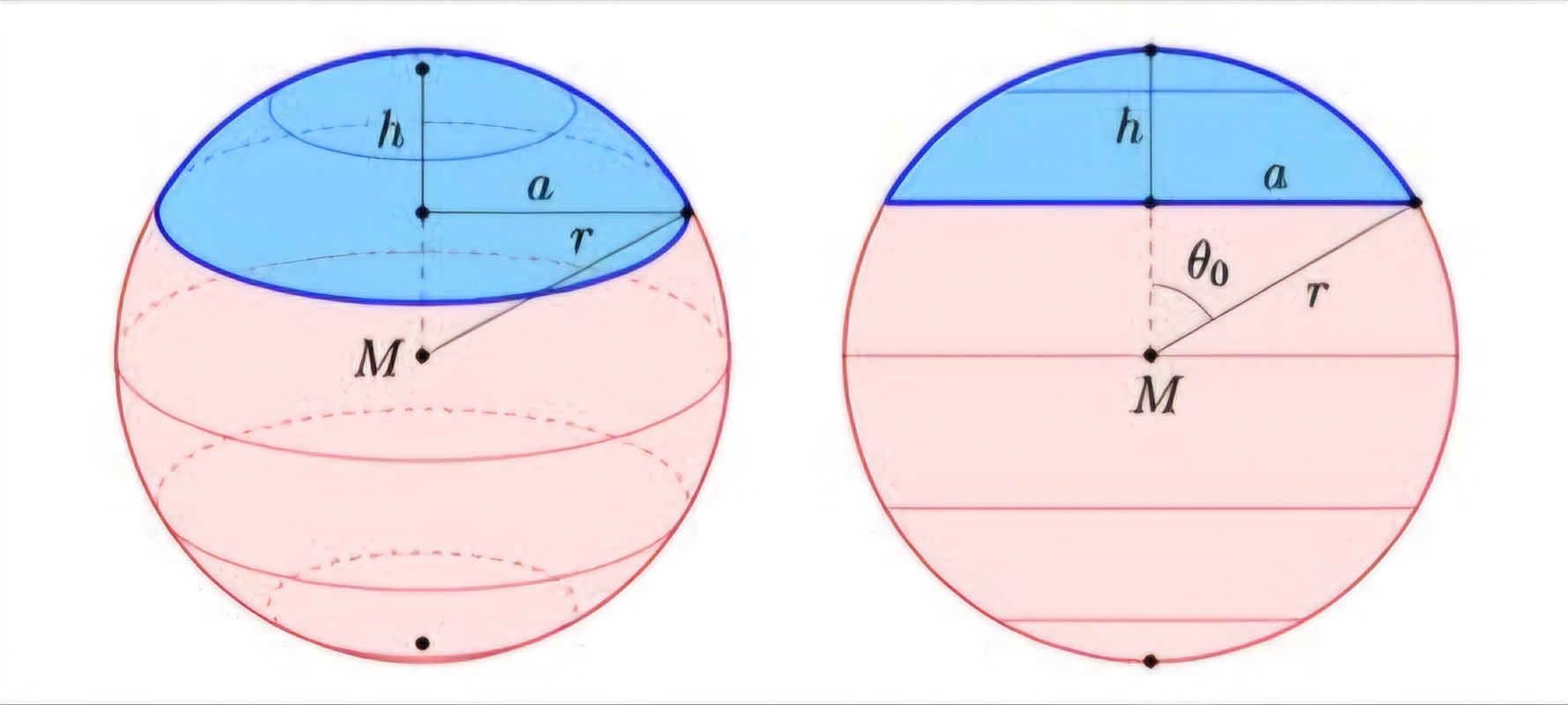
Diện tích + Thể tích chỏm cầu

1. S = π(a² + h²)

2. V = (πh / 6) (h² + 3a²) = (πh² / 3) (3r - h)

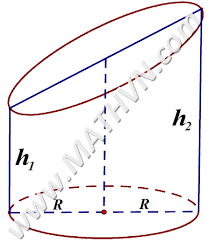
Diện tích xung quanh- Thể tích trụ cụt

1. S = πR (h₁ + h₂)

2. V = πR² * (h₁ + h₂) / 2

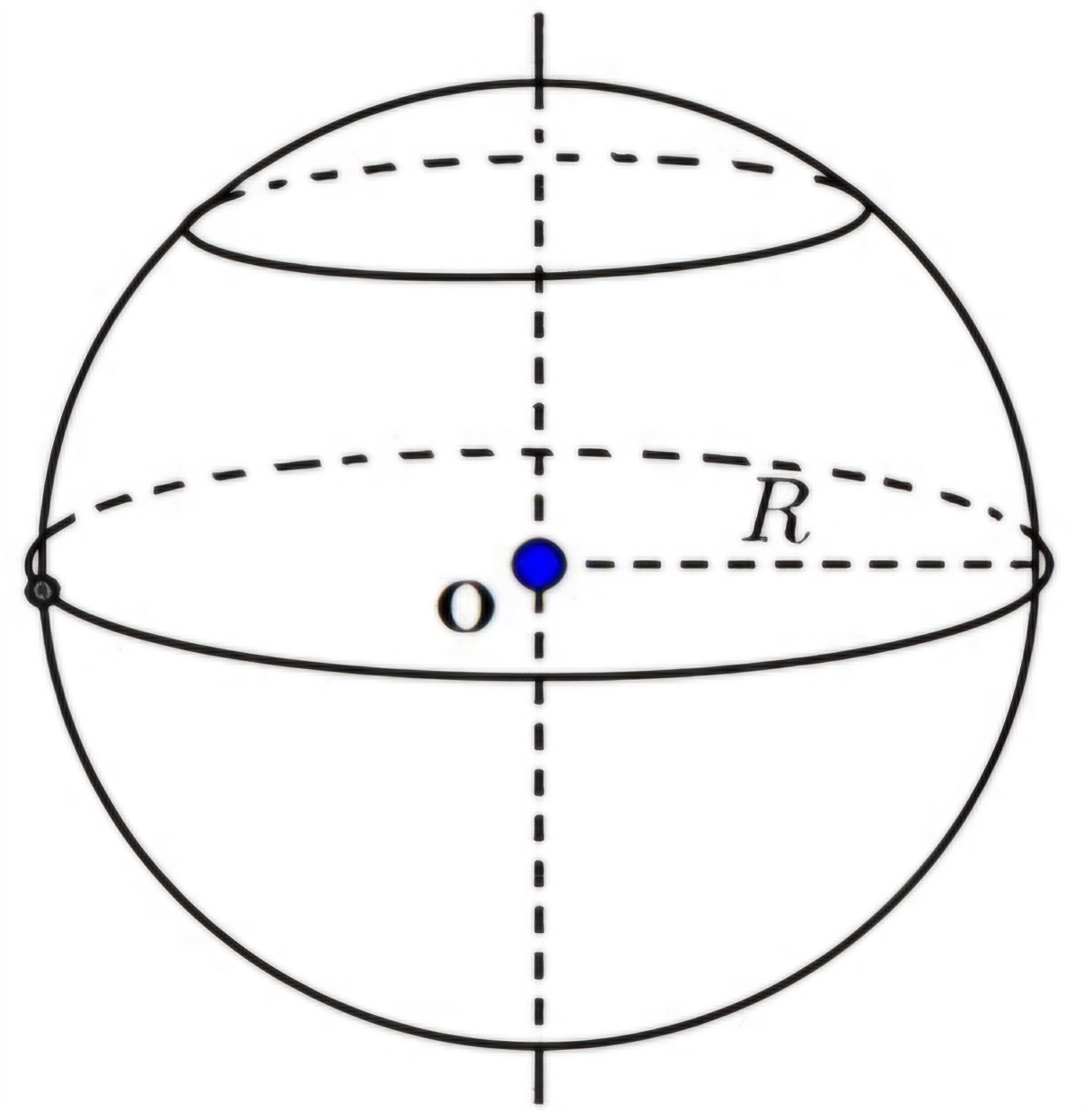
Diện tích + Thể tích hình cầu

1. S = 4πR²

2. V = (4/3)πR³

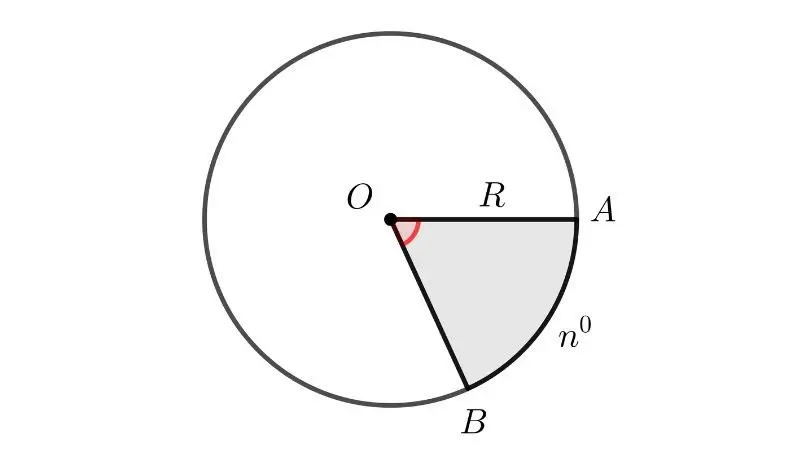
Độ dài cung tròn + Diện tích hình quạt tròn

1. l = (π * R * n) / 180

2. S = (π * R² * n) / 360

Công thức tính trung vị

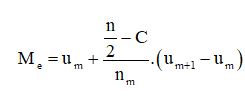
Công thức tính mốt

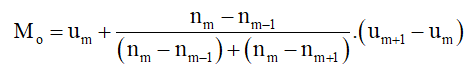
Ptđt đi qua 2 cực trị của hàm bậc hai trên bậc 1

(đạo hàm tử : đạo hàm mẫu)

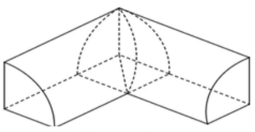
Thể tích phần giao giữa 1/4 hai hình trụ vuông góc, cùng bán kính R

V = 2R³/3

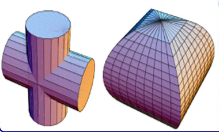
Thể tích phần giao giữa hai hình trụ vuông góc, cùng bán kính R

V = 16R³/3

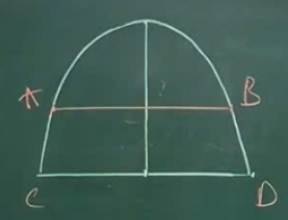
Mối liên hệ diện tích trong parabol

S_parabol nhỏ / S_parabol lớn = (AB / CD)^3

Trục thực: F₁F₂ = 2c

Trục ảo: A₁A₂ = 2a

Phương trình Hypebol: x²/a² - y²/b² = 1

Quy tích điểm M thỏa mãn I MF1-MF2 I = 2a là hình Hypebol với F₁F₂ = 2c, b² = c² - a²

Trục lớn: A₁A₂ = 2a

Trục bé: B₁B₂ = 2b

Phương trình Elip: x²/a² + y²/b² = 1

Quy tích các điểm M thỏa mãn MF1+MF2 = 2a là hình Elip với F₁F₂ = 2c, b² = a² - c²

Khối tròn xoay Elip quanh Ox, Oy

Quanh Ox: V = 4/3πab²

Quanh Oy: V = 4/3πa²b