Chapter 5: Gravitation
Gravitational Energy:
Gravitational energy is the energy possessed by an object due to its position in a gravitational field.
The gravitational potential energy of an object in a uniform gravitational field can be calculated using the formula: PE = mgh, where m is the mass of the object, g is the acceleration due to gravity, and h is the height of the object.
The gravitational potential energy of an object in a non-uniform gravitational field can be calculated using the integral of the gravitational force over the distance moved.
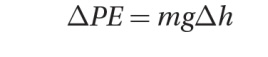
We now know that the value of g is not constant but varies inversely with the square of the distance from the center of Earth. Also, since we want the potential energy to become smaller the closer we get to Earth, we can use the results of the previous section to rewrite the potential energy formula as:
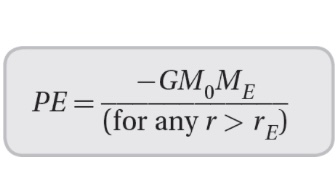
Gravitational energy is a form of potential energy and can be converted into other forms of energy, such as kinetic energy, as the object falls toward the source of the gravitational field.
The total energy of an object in a gravitational field is the sum of its gravitational potential energy and its kinetic energy and is conserved as the object moves within the field.
TIP:
Notice that the acceleration due to gravity does not depend on the mass of the falling object. This is consistent with Galileo's observations of falling bodies and the period of a pendulum.
Gravitational energy is an important concept in many fields, including astrophysics, geology, and engineering.
The gravitational potential energy of an object is always negative since it is defined as the work done by gravity to move the object from an infinite distance to its current position.
Gravitational energy plays a key role in the formation and evolution of celestial bodies, such as stars, planets, and galaxies.
The gravitational potential energy of an object can be used to calculate the escape velocity required to leave the gravitational field of a planet or other celestial body.
An object can leave the surface of Earth with any velocity. There is, however, one minimum velocity at which, if the spacecraft coasted, it would not fall back to Earth because of gravity.
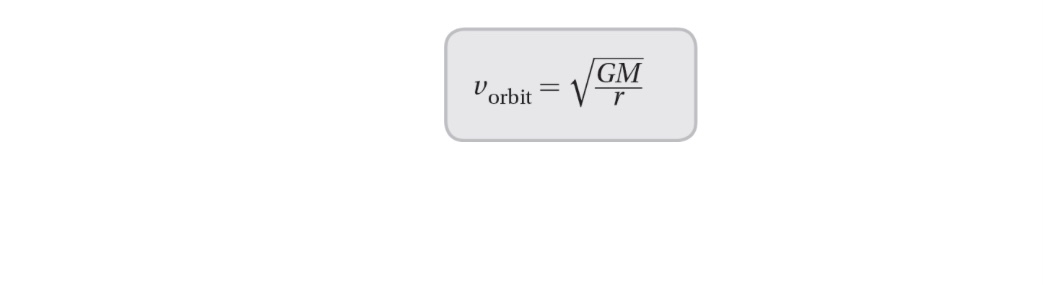
The orbital velocity can be determined by assuming that we have an approximately circular orbit (see Chapter 2). In this case, we can set the centripetal force equal to the gravitational force:
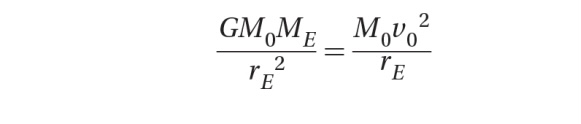
Eliminating the mass of the object from the equation leaves:
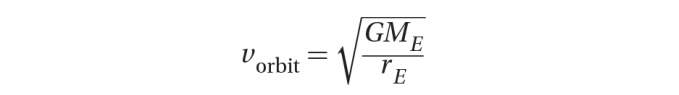
By comparing the two expressions for escape velocity and orbital velocity, we see that:
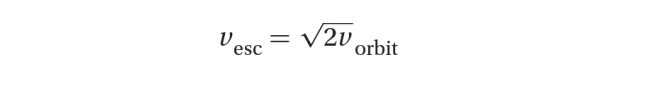
Of course, we could repeat our derivation of orbital speed for any planet of arbitrary mass M and any arbitrary orbital radius r:
Newton's Law of Universal Gravitation:
Newton's law of universal gravitation states that every particle in the universe attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
The gravitational force between two objects can be calculated using the formula: F = G (m1m2) / r^2, where F is the gravitational force, m1 and m2 are the masses of the two objects, r is the distance between them, and G is the gravitational constant.
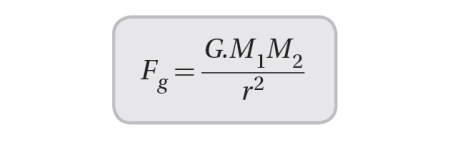
The gravitational constant is a fundamental constant of nature that determines the strength of the gravitational force between two objects.
Newton's law of universal gravitation applies to all objects in the universe, from the smallest subatomic particles to the largest galaxies.
The gravitational force between two objects is always attractive, meaning it pulls the objects towards each other.
Newton's law of universal gravitation is a cornerstone of modern physics and has enabled scientists to understand and predict the behavior of celestial bodies, including the motion of planets, moons, and comets.
Newtons Laws
Newton's First Law states that an object at rest will remain at rest, and an object in motion will remain in motion with a constant velocity unless acted upon by an unbalanced force. This law is also known as the law of inertia, and it describes how an object's motion will not change unless an external force acts upon it.
Newton's Second Law relates the net force acting on an object to its acceleration. The law states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. This law can be expressed mathematically as F=ma, where F is the net force, m is the mass of the object, and a is its acceleration.
Newton's Third Law states that for every action, there is an equal and opposite reaction. This law describes how forces always exist in pairs, and the force exerted by one object on another is always equal in magnitude but opposite in direction to the force exerted by the second object on the first.
Newton's laws apply to both objects in equilibrium and those that are accelerating. In equilibrium, the net force acting on an object is zero, and the object is either at rest or moving with a constant velocity. In cases where objects are accelerating, the net force acting on the object is not zero, and the object's motion changes accordingly.
The laws of motion are not absolute but are dependent on the reference frame from which they are observed. This means that the same physical situation can be described differently depending on the observer's point of view. Additionally, Newton's laws only apply in situations where the forces acting on the objects are classical forces, such as gravitational or electromagnetic forces. In situations involving quantum mechanics or relativistic physics, these laws may not apply.
\n