AP Physics 2 Ultimate Guide

Fluids

Substances which can flow.

Density

Mass per unit volume of a substance

S.I. Units of Density

kg/m³

CGS unit of density

g/cc

Pressure

Magnitude of normal force acting per unit area

S.I. Units of Pressure

Pascal

Hydrostatic pressure

Pressure due to liquid

Factors that hydrostatic pressure depends on

Density of liquid and depth below the surface

What principle does buoyancy use?

Archimedes Principle

Buoyancy

If a body is fully or partially immersed in a fluid, it experiences an upward force due to the fluid called buoyant force.

An object with a mass of 150 kg and a volume of 0.75 m3 is floating in ethyl alcohol, whose density is 800 kg/m3. What fraction of the object’s volume is above the surface of the fluid?

Volume Flow Rate

Volume of fluid that passes through a particular point per unit of time.

Formula for volume flow rate

F = Av

A = cross-sectional area

v=flow speed

Continuity equation

The density of fluid is constant. Thus, A1V1 = A2V2.

A circular pipe of non-uniform diameter carries water. At one point in the pipe, the radius is 2 cm and the flow speed is 6m/s. What is the flow speed at a point where the pipe constricts to a radius of 1 cm?

Bernoulli’s effect

At comparable heights, the pressure is lower where the flow speed is greater.

Bernoulli’s Equation

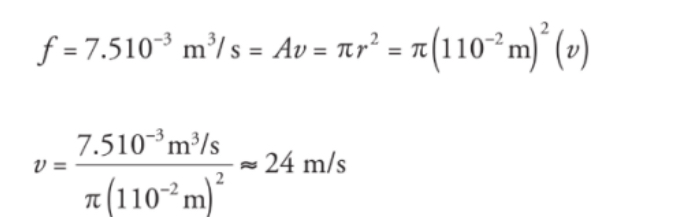
Buoyancy diagram for object floating in liquid.

Practical units for pressure

atm, bar, torr

A vertical column made of cement has a base area of 0.5 m2. If its height is 2 m, and the density of cement is 3000 kg/m3, how much pressure does this column exert on the ground?

SI unit for Volume Flow Rate

m³/s

A circular pipe of non-uniform diameter carries water. At one point in the pipe, the radius is 2 cm and the flow speed is 6m/s. What is the volume flow rate?

What does Bernoulli’s Equation assume for the conservation of energy in fluids?

The fluid is incompressible.

The fluid’s viscosity is negligible.

The fluid is streamlined.

Bernoulli’s Equation

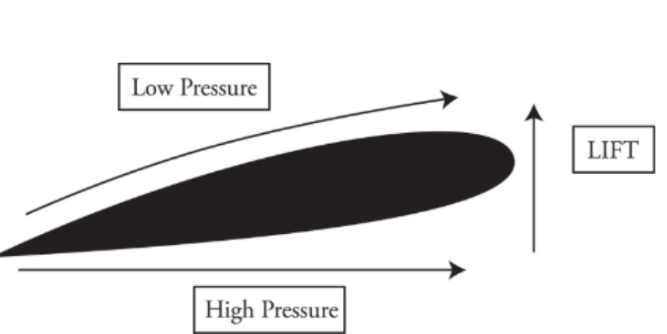
Explain how airflow affects the airplane wing in the image and helps it fly.

The air on the bottom has greater pressure and pushes up on the wing, giving the airplane lift force.

Heat

Thermal energy is transmitted from one body to another.

Energy in transit.

Temperature

It is a measure of an object’s internal energy.

Kinetic Theory of Gases

• It relates to the macroscopic properties of gases such as pressure, temperature, etc.

• Every gas consists of small particles known as molecules.

• The gas molecules are identical but different from those of another gas.

• The volume of molecules is negligible compared to the volume of gas.

• The density of a gas is constant at all points.

• Consequently, pressure is exerted by gas molecules on the walls of the container.

• No attractive or repulsive force exists between the gas molecules.

The Ideal Gas Law

Pv = nRT

• P = pressure

• V = volume

• n = no. of moles

• R = Gas constant

• T = temperature

Average Kinetic Energy

The pressure exerted by N molecules of gas in a container is related to the average kinetic energy.

K avg = 3/2 kb T

• K avg = average kinetic energy

• kb = Boltzmann’s constant

• T = temperature

Room mean square velocity

It gives us a type of average speed that is easy to calculate from the temperature of the gas.

vrms = √3 kb T/ m

• vrms = root mean square velocity

• kb = Boltzmann’s constant

• T = temperature

• m = mass

The Maxell-Boltzmann Distribution

• The Kinetic theory of gases applies to a large number of particles.

• Some molecules will be moving faster than average and some much slower.

Heat Engines

It is a device which uses heat to produce useful work.

Convection

The movement caused within a fluid by the tendency of hotter and therefore less dense material to rise, and colder, denser material to sink under the influence of gravity, which consequently results in transfer of heat.

Radiation

Emission or transmission of energy in the form of waves or particles through space or through a material medium.

Zeroth Law of Thermodynamics

If objects 1 and 2 are in thermal equilibrium with Object 3, then Objects 1 and 2 are in thermal equilibrium with each other.

First Law of Thermodynamics

It is a special case of the law of conservation of energy that describes processes in which only internal energy changes and the only energy transfers are by heat and work.

∆ U = Q + W

• Q = heat added

• W = work done by the system

• ∆ U = change in internal energy

Work done

It is used to calculate work done

Isothermal Process

Temperature remains constant

Adiabatic Process

No transfer of heat

Isobaric Process

Pressure remains constant

Isochoric Process

Volume remains constant

Second Law of Thermodynamics

It describes how systems evolve over time.

Entropy

It is associated with a state of randomness, disorder, or uncertainty

Conduction

Heat conducts from one point to another only if there is a temperature difference between the two objects.

Electric Charge

• In an isolated system, the charge is always conserved.

• Protons and electrons have a quality called electric charge.

• The charge is invariant in nature.

• The charge is quantized.

• (Q = n e)

  • e = 1.6 * 10^-19 C

  • n = no. of electrons

  • Q = charge

Ionization

Coulomb’s Law

The electric force between two particles with charges q1 and q2 separated by distance r has a magnitude by the equation:

F = Kq1q2/r^2

• F = force

• K = coulomb’s constant

• q1 and q2 = charges

• r = distance between the charges

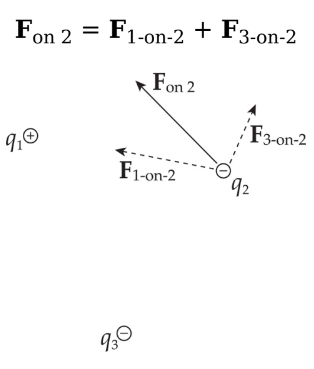
Addition of forces

Consider three point charges: q1, q2, and q3. The total electric force acting on, say, is simply the sum of F1-on-2, the electric force on q2 due to q1, and F3-on-2, the electric force on q2 due to q3:

Electric Field

The space is surrounded by a charge in which another charged particle experiences the force.

E = F on q/ q

It describes the electric field vector from the force vector on a positive charge.

Electric field due to a point charge

The electric field surrounding the point charge is:

E = 1/4πε0 * Q/r^2

• E = electric field

• Q = charger = distance between charges

• ε0 = permittivity of free space

Three types of electric field

• Radial field

• It is generated by a collection of point charges.

• An infinite sheet of charge.

electric field lines

• The electric fields follow the same addition properties as the electric force.

• The electric field lines never cross.

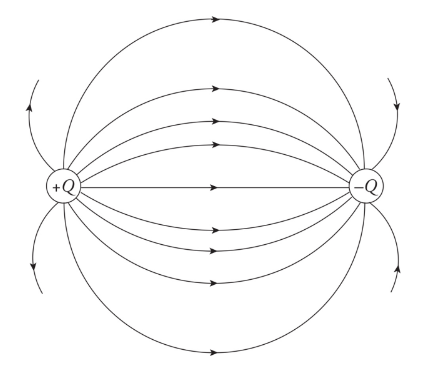
The uniform electric field

A lot of problems deal with the uniform electric field. The field may be taken as uniform at least in the middle. The uniform field just signifies the constant force.

Conductors

Materials which allow the flow of excess charge without resisting it.

Insulators

Materials that resist the flow of electrons.

Charging by friction

It involves rubbing the insulator against another material, thereby stripping electrons from one to another material.

Charging through conduction

When we connect two conductors charge flows from one to another until the potential of both the conductors becomes the same.

Charging through induction

The process of charging by induction may be used to redistribute charges among a pair of neutrally charged spheres.

If the sphere is an insulator made up of glass

There aren’t any free electrons. The atoms make up the sphere will become polarised.

charge of proton

positive

charge of electron

negative

law of charges

the directions of the electric forces on the charges of mutual interaction; like charges repel, opposite charges attract.

net charge

an object with an excess of positive or negative charges

electrostatic charging

accomplished by Friction, Contact, Induction, or Polarization

Charging by Polarization

Charging by Polarization

How do objects become charged?

By gaining/losing electrons

Electric charge is always _______.

Conserved

What is the numerical value of one charge?

1 e = 1.6 x 10^-19 Coulombs

The SI unit of a charge is in ______.

coulombs

What happens when an insulator is charged?

Only the small spot which was directly contacted with a charge remains charged.

What is the name of materials that contain properties somewhere between conductors and insulators?

semiconductors

A dipole consists of:

two equal and opposite charged

In what direction to field lines go?

From positive to negative charges ALWAYS

What indicated field strength?

The density of field lines

What do few field lines between charges indicate?

a weak field

Which one of the following rules, laws, or principles describes how the net electric charge of an isolated system undergoing any process remains constant?

law of conservation of electric charge

Electrical Potential Energy

We is the work done by the electric force, then the change in the charge’s electrical potential energy is defined by:

Ue = electrical potential energy

We = work done by electric force

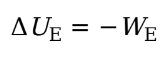
Electrical Potential Energy from a point charge

Electrical potential energy required to move along the field lines surrounding a point charge is given by:

• q1 and q2 = charges

• e0 = permeability of free space

• Ue = electrical potential energy

• r = distance

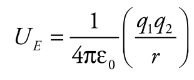
Electric Potential

Electric potential is the electric potential energy per unit of charge at a point in an electric field, measured in volts (V). It's the work done per unit charge in bringing a test charge from infinity to that point.

V = U/q

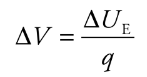
Electric Potential Energy from a point charge

Consider the electric field created by a point source charge Q. If a charge moves from a distance rA to a distance rB from Q, then the change in the potential energy is:

• Ub and Ua = electrical potential energies for a and b

• ra and rb = distances for a and b

• e0 = permeability of free space

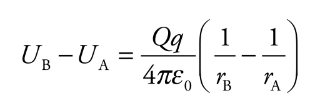
Equipotential Surface

An equipotential surface is a surface in a region of space where every point on the surface is at the same potential. In other words, no work is required to move a charge along an equipotential surface. Equipotential surfaces are perpendicular to electric field lines and can be used to visualize the electric field in a given region.

Addition of electric potential

V = kQ/r

• V = electric potential energy

• q = point charger = distance between any point around the charge to the point charge

• k = Coulomb constant; k = 9.0 × 109 N

Equipotential Curve

Equipotential curves are curves of constant elevation. If you walk along any of the contour lines and you neither ascend nor descend, then the curve is known as the equipotential curve.

Equipotential Map

A drawing of several equipotential curves at various values of the potential for a charge distribution is called an equipotential map.

Capacitor

Two conductors, separated by some distance carry equal but opposite charges +Q and -Q. The pair comprises a system called a capacitor.

Parallel-Plate Capacitor

The capacitor is in the form of parallel metal plates or sheets.

Capacitance

The capacitance measures the capacity for holding charge.

C = κε₀A/d (k = dielectric constant)

Fringing fields

Fringing fields extend beyond conductor or magnetic material edges. They weaken as the distance from the edge increases. They're important in device design but can cause interference and affect performance.

energy stored in capacitor

The energy stored in a capacitor can be calculated using the formula

Uc = ½QV = ½CV² where

U is the energy stored in joules, C is the capacitance of the capacitor in farads and V is the voltage across the capacitor in volts.

Dielectric

To keep the plates of the capacitor apart they are filled with dielectric which increases the capacitance of the capacitor.

The amount of work done by a uniform electric field

W = q E d

• W = work done

• q = charge

• E = electric field

• d = distance

A dielectric always _______ the capacitance of a capacitor

increases

the __________ of the capacitance of a collection of capacitors in series is found by adding the reciprocals of the individual capacitances

reciprocal

Collection of capacitors is said to be in ______ if they all share the same charge magnitude

series

The equivalent capacitance of a collection of capacitors in parallel is found by _______ the individual capacitances

adding

The equivalent capacitance of a collection of capacitors in parallel is found by _______ the individual capacitances

parallel

1 C/V = ?

1 Farad

Ratio of charge to potential difference (C=Q/∆V)

capacitance

Magnitude of the potential difference between two plates of a distance d

∆V = -Ed