Calc 2 - Hyperbolic, Improper Integrals, Sequences, Monotone Sequences, Series of Constants, Series of Functions, & Power Series

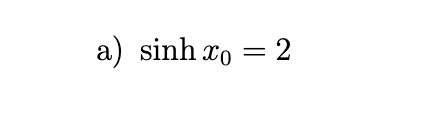
In each part, a value for one of the hyperbolic functions is given at an unspecified positive number x0. Use appropriate identities to find the exact values of the remaining five hyperbolic functions at x0.

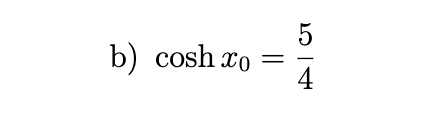
In each part, a value for one of the hyperbolic functions is given at an unspecified positive number x0. Use appropriate identities to find the exact values of the remaining five hyperbolic functions at x0.

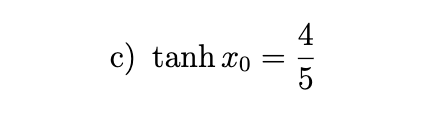
In each part, a value for one of the hyperbolic functions is given at an unspecified positive number x0. Use appropriate identities to find the exact values of the remaining five hyperbolic functions at x0.

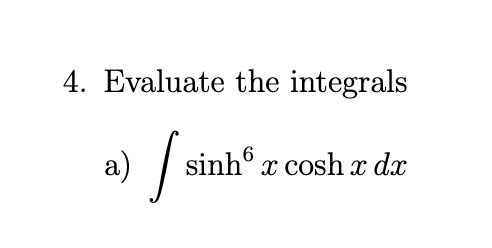
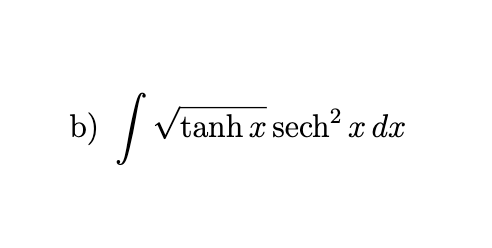
evaluate

2/3(tanh^3/2 x) + C

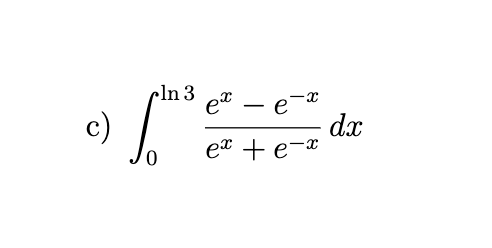
evaluate

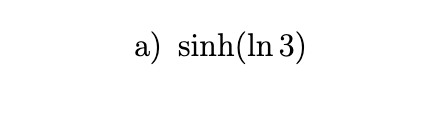
Find the exact numerical value of each expression.

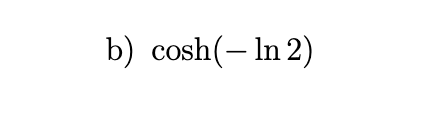
Find the exact numerical value of each expression.

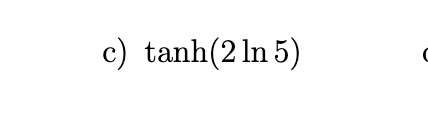
Find the exact numerical value of each expression.

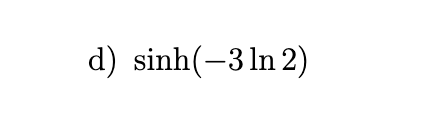
Find the exact numerical value of each expression.

-63/16

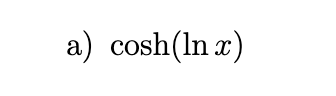
In each part, rewrite the expression as a ratio of polynomials

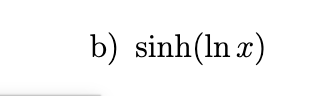
In each part, rewrite the expression as a ratio of polynomials

(x² - 1)/2x

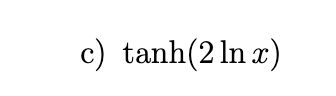
In each part, rewrite the expression as a ratio of polynomials

(x⁴ -1)/(x⁴ +1)

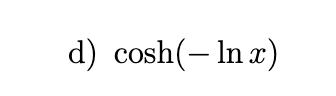
In each part, rewrite the expression as a ratio of polynomials

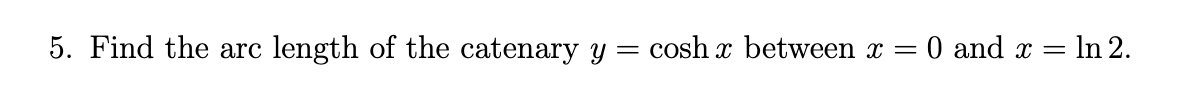
3/4

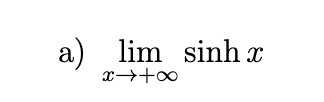
Find the following limits, and confirm that they are consistent with the graphs of the functions involved in each case.

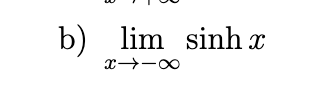
Find the following limits, and confirm that they are consistent with the graphs of the functions involved in each case.

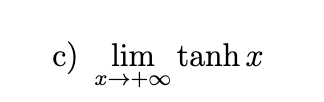
Find the following limits, and confirm that they are consistent with the graphs of the functions involved in each case.

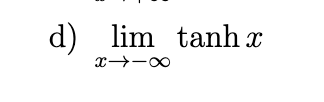
Find the following limits, and confirm that they are consistent with the graphs of the functions involved in each case.

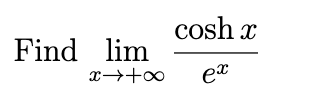
1/2

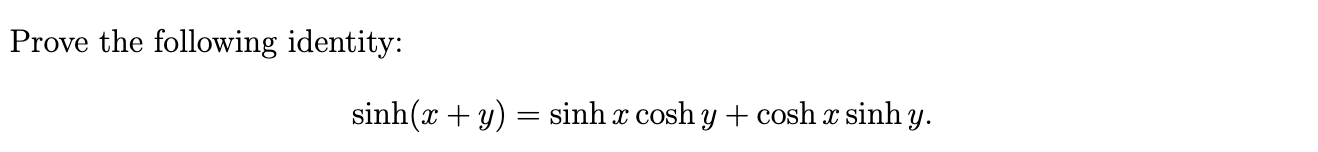
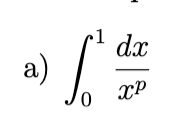
In each part, determine all values of p for which the integral is improper

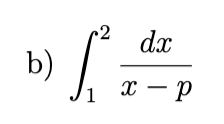
In each part, determine all values of p for which the integral is improper

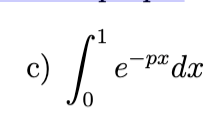
In each part, determine all values of p for which the integral is improper

never improper

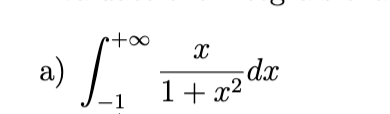
diverges

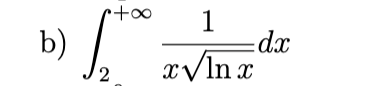
divergent

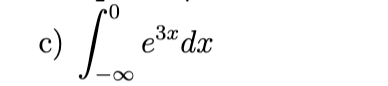
convergent to 1/3

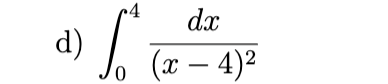
Divergent

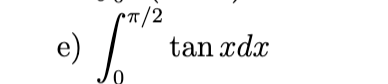
Divergent

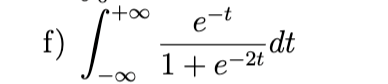
Convergent to pi/2

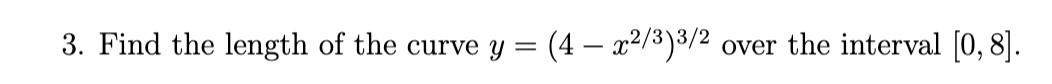
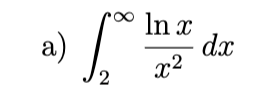
convergent

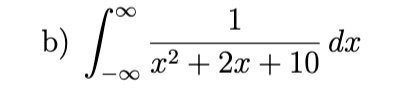
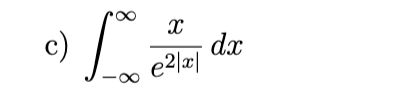
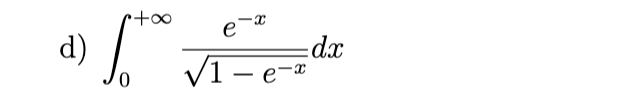
hint:

Use the substitution u = 1 − e^(-x)

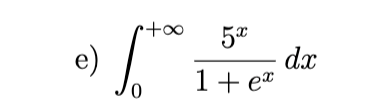
5ln(2) (hint: use substitution)

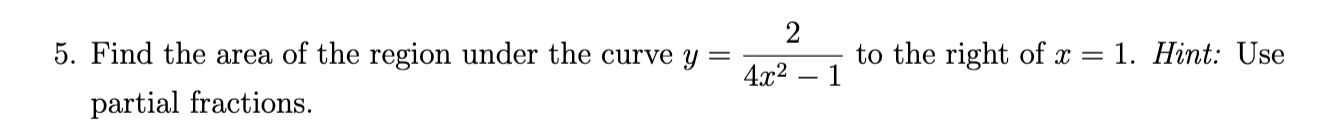
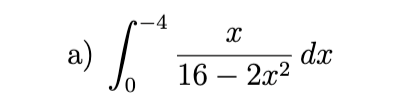
Divergent

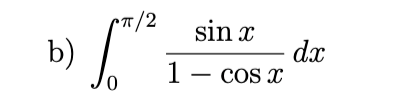
-inf, divergent

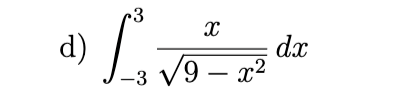
converges to 0

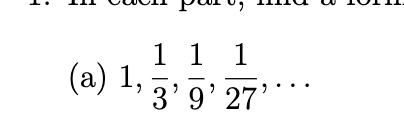
In each part, find a formula for the general term of the sequence, starting with n = 1

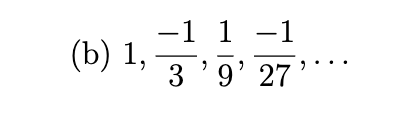
In each part, find a formula for the general term of the sequence, starting with n = 1

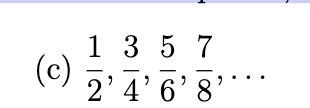
In each part, find a formula for the general term of the sequence, starting with n = 1

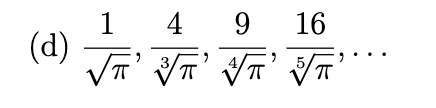
In each part, find a formula for the general term of the sequence, starting with n = 1

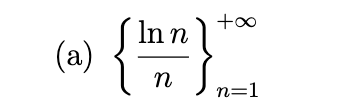
Write out the first five terms of the sequence, determine whether the sequence converges, and if so find its limit.

Convergent (limit = 0)

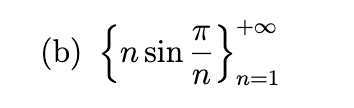
Write out the first five terms of the sequence, determine whether the sequence converges, and if so find its limit.

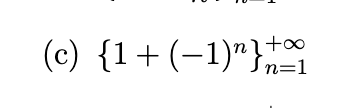
Write out the first five terms of the sequence, determine whether the sequence converges, and if so find its limit.

diverges

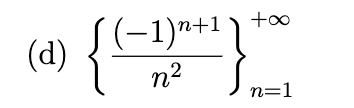
Write out the first five terms of the sequence, determine whether the sequence converges, and if so find its limit.

Convergent

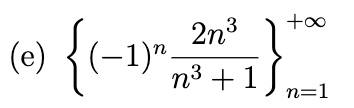
Write out the first five terms of the sequence, determine whether the sequence converges, and if so find its limit.

divergent (oscillating between 2 and -2)

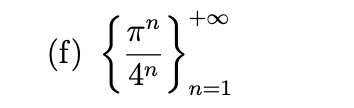
Write out the first five terms of the sequence, determine whether the sequence converges, and if so find its limit.

Converges to 0

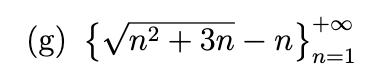
Write out the first five terms of the sequence, determine whether the sequence converges, and if so find its limit.

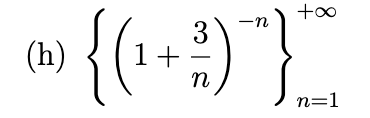
Write out the first five terms of the sequence, determine whether the sequence converges, and if so find its limit.

convergent (1/e³)

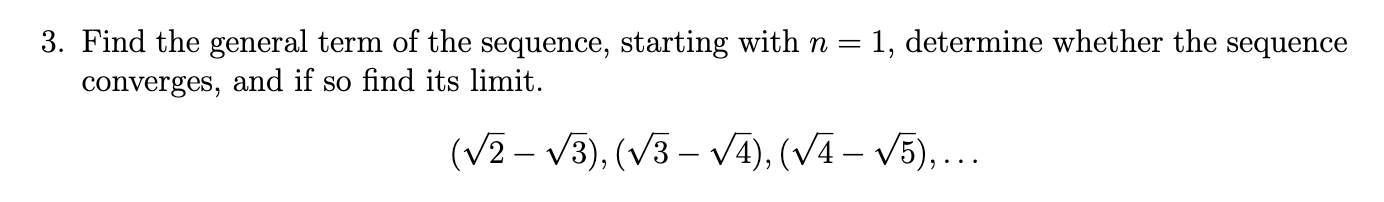
converges, limit =0

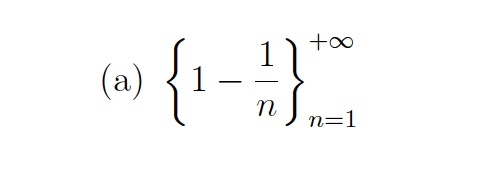
Use the difference a(n+1) − an to show that the given sequence {an} is strictly increasing or

strictly decreasing.

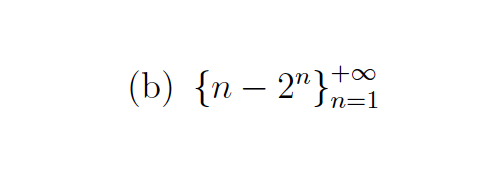
Use the difference a(n+1) − an to show that the given sequence {an} is strictly increasing or

strictly decreasing.

strictly decreasing

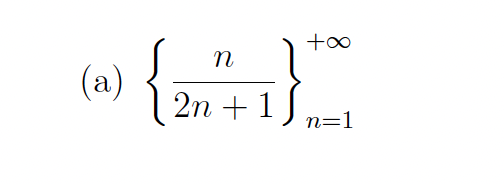
Use the ratio an+1/an to show that the given sequence {an} is strictly increasing or strictly

decreasing.

strictly increasing

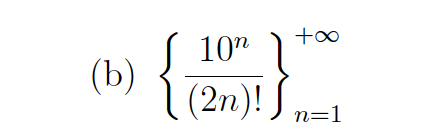
Use the ratio an+1/an to show that the given sequence {an} is strictly increasing or strictly

decreasing.

strictly decreasing

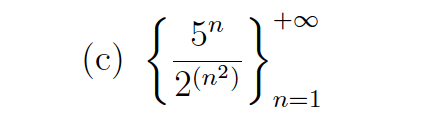
Use the ratio an+1/an to show that the given sequence {an} is strictly increasing or strictly

decreasing.

strictly decreasing

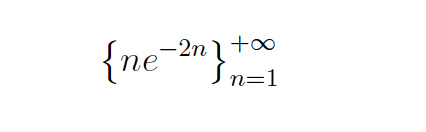
ignore

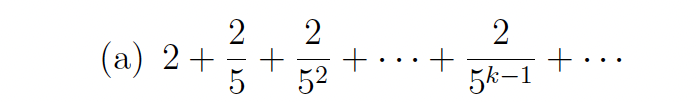
In each part, find exact values for the first three partial sums, find a closed form for the nth

partial sum, and determine whether the series converges by calculating the limit of the nth

partial sum. If the series converges, then state its sum.

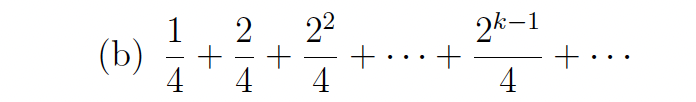
In each part, find exact values for the first three partial sums, find a closed form for the nth

partial sum, and determine whether the series converges by calculating the limit of the nth

partial sum. If the series converges, then state its sum.

Divergent

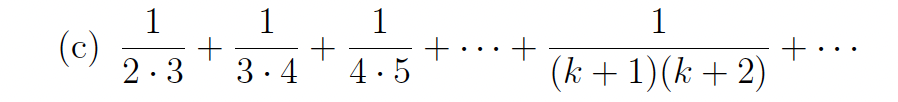
In each part, find exact values for the first three partial sums, find a closed form for the nth

partial sum, and determine whether the series converges by calculating the limit of the nth

partial sum. If the series converges, then state its sum.

Convergent to 1/2

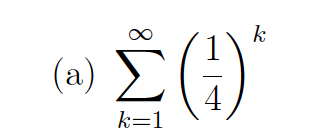
In each part, determine whether the series converges or diverges. If the series converges,

then state its sum.

Convergent, sum = (1/4)/(1-1/4)

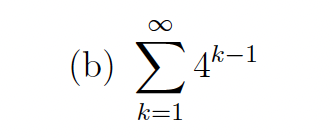
In each part, determine whether the series converges or diverges. If the series converges,

then state its sum.

divergent (ratio is greater than 1)

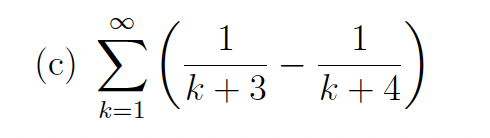
In each part, determine whether the series converges or diverges. If the series converges,

then state its sum.

converges and convergent to 1/4

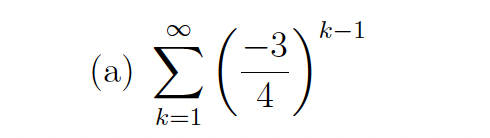
Determine whether the series converges, and if so find its sum

Convergent, sum = 4/7

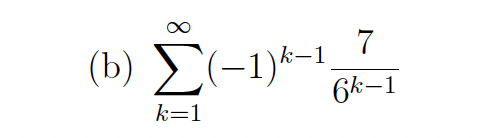
Determine whether the series converges, and if so find its sum

Convergent, sum = 6

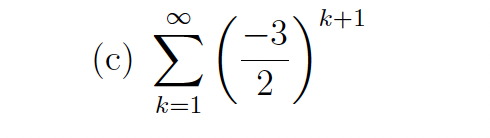
Determine whether the series converges, and if so find its sum

divergent

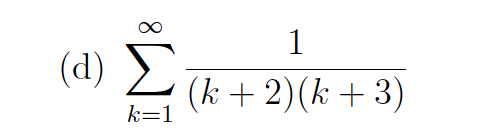
Determine whether the series converges, and if so find its sum

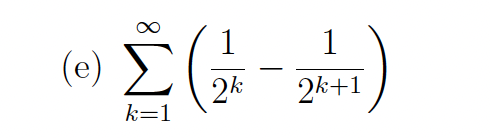
Determine whether the series converges, and if so find its sum

convergent (1/2)

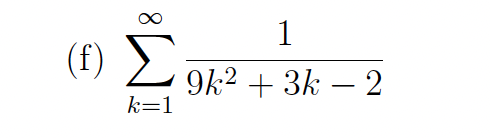
Determine whether the series converges, and if so find its sum

Convergent, sum =1/6

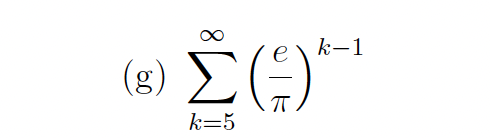
Determine whether the series converges, and if so find its sum

convergent

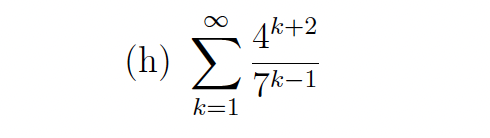
Determine whether the series converges, and if so find its sum

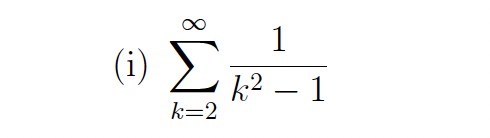
Determine whether the series converges, and if so find its sum

convergent and its sum is ¾ (PFD)

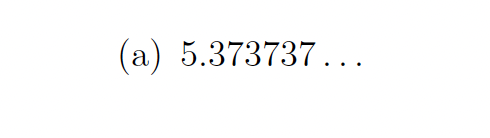
Express the repeating decimal as an irreducible fraction.

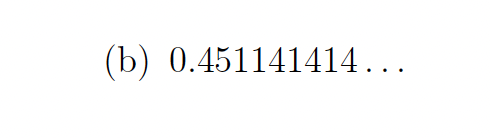
Express the repeating decimal as an irreducible fraction.

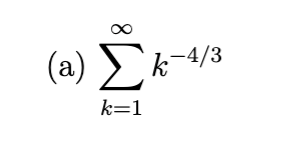
convergent

Divergent

convergent p series

covergent

divergent

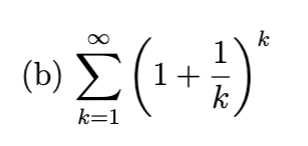
divergent (e)

Divergent (grandi’s series)

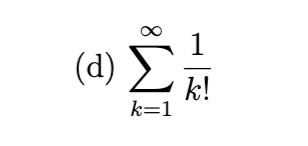
converges

Convergent

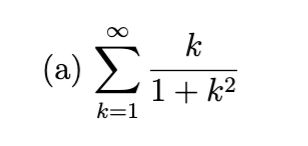
divergent (ordinary comp test)

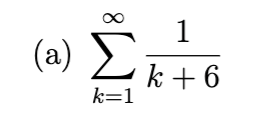
diverges

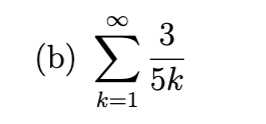
divergent

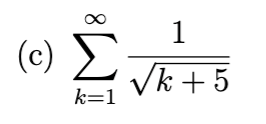
diverges

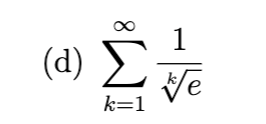
divergent

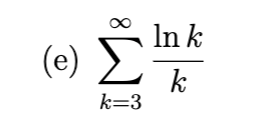
divergent

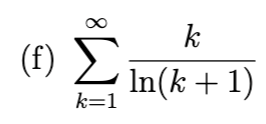
divergent

Convergent