Geometry Terms Module 4

transversal

a line that intersects two coplanar lines at two different points

corresponding angles

lie on the same side of the transversal and same sides of the intersecting line.

same-side interior angles

lie on the same side of the transversal and between the intersected lines.

alternate interior angles

nonadjacent angles that lie on opposite sides of the transversal between the intersected lines.

alternate exterior angles

lie on opposite sides of the transversal and outside the intersected lines

parallel lines

lie in the same plane and never intersect

same-side interior angles postulate

If two parallel lines are cut by a transversal, then the pair of same-side interior angles are supplementary.

alternate interior angles theorem

If two parallel lines are cut by a transversal, then the pairs of alternate interior angles have the same measure.

corresponding angles theorem

If two parallel lines are cut by a transversal, then the pairs of corresponding angles have the same measure.

postulate

does not need to be proven

theorem

needs to be proven

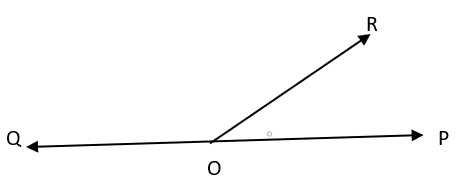
linear pair

adjacent supplementary angles

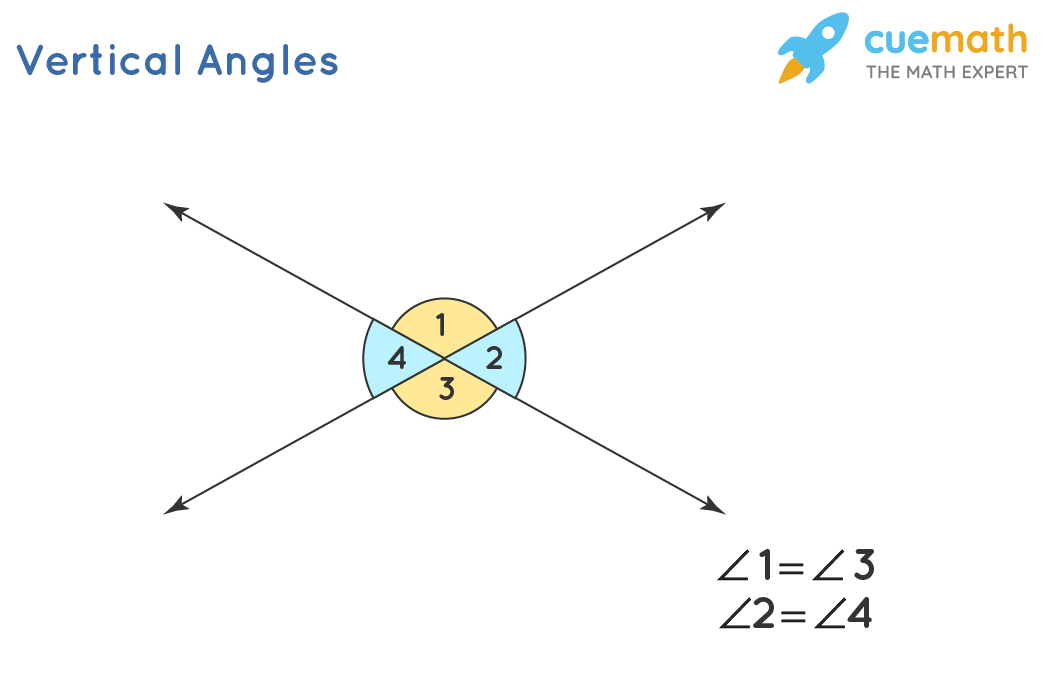
vertical angles

when 2 lines intersect, vertical angles are congruent

converse of same-side interior angles postulate

If two lines are cut by a transversal, the same-side interior angles are supplementary, then the lines are parallel

converse of the alternate interior angles theorem

If two lines cut by a transversal so that any pair of alternate interior angles are congruent, then the lines are parallel

converse of the corresponding angles theorem

If two lines are cut by a transversal so that any pair of corresponding angles are congruent, then the lines are parallel

what is a converse?

a rephrased postulate or theorem

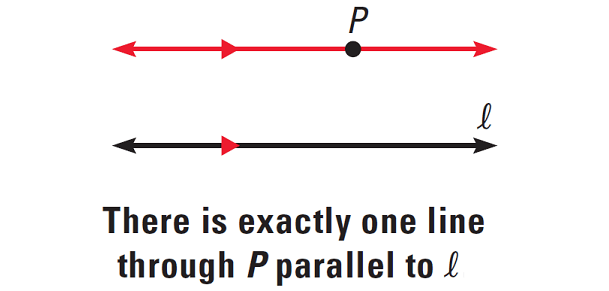
The parallel postulate

Through a point P not on line L, there is exactly one line parallel to L.

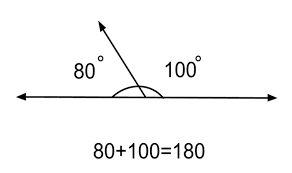
linear pair theorem

If two angles form a linear pair, then the measure of the angles add up to 180

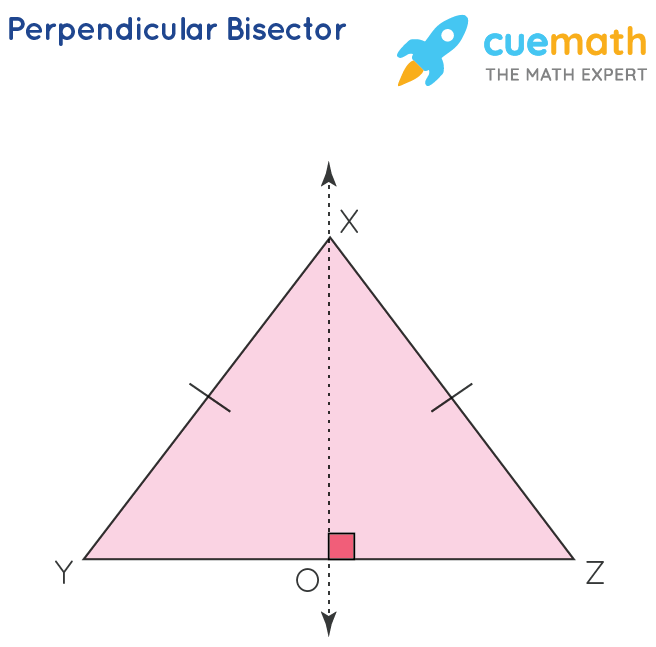
Perpendicular Bisector Theorem

If a point is on the perpendicular bisector of a segment, then it is equidistant from the end points of a segment

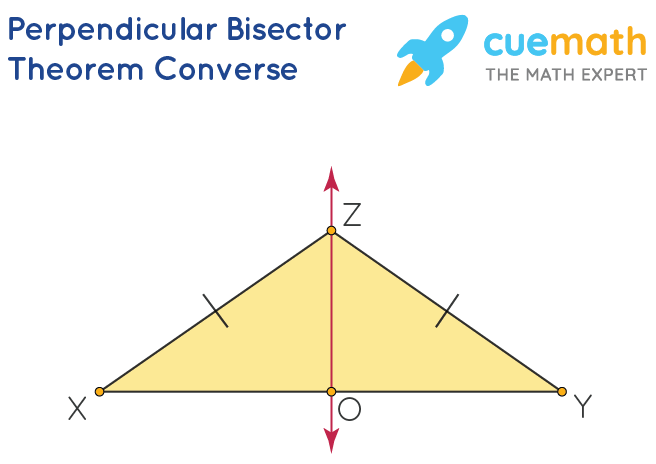
Converse of the Perpendicular Bisector Theorem

If a point is equidistant from the endpoints of a segment, then it lies on the perpendicular bisector of the segment

vertical angles theorem

If two lines intersect, the vertical angles are congruent

slope intercept form of a line

y=mx+b

point-slope form of a line

y-y1=m(x-x1)

pythagorean theorem

a² + b² =c²

definition of supplementary angles

two angles that add up to 180

definition of complementary angles

two angles that add up to 90

definition of perpendicular lines

when two lines intersect forming 90 degree angles