Physics

Dot Product (A * B = ?)

a · b = |a| × |b| × cos(θ)

Used to generate a scalar quantity

Cross Product (A x B = ?)

a × b = |a| |b| sin(θ) n

n = Unit Vector in plane perpendicular to a and b

SI Unit for Force

Newton (N) = (kg*m)/s²

Magnitude of the Gravitational Force (Fg = ?)

Fg = Gm1m2/r²

G = Universal Gravitational Constant = 6.67 × 10^-11 (N*m²)/kg²

Static Friction (fs)

0 ≤ Fs ≤ μ_sN

μ_s is the coefficient of static friction

Exists between a stationary object and the surface upon which it rests

Kinetic Friction

F_k = μ_k * N

Exists between a sliding object and the surface over which the object slides

Relationship between Weight and Mass (F_g = ?)

F_g = mg

F_^g = Weight of the object

g = Acceleration due to gravity = 9.8 m/s²

Center of Mass (x = , y = , z = ?)

x = (m₁×₁ + m₂×₂ + …)/ (m₁ + m₂ + …)

y = (m₁y₁ + m₂y₂ + …)/ (m₁ + m₂ + …)

z = (m₁z₁ + m₂z₂ + …)/ (m₁ + m₂ + …)

x-, y-, and z-values are coordinates

Newton’s First Law

A body either at rest or in motion with constant velocity will remain that way unless a net force acts upon it (Law of Inertia)

F_net = ma = 0

Newton’s Second Law

An object of mass m will accelerate when the vector sum of the forces results in some nonzero resultant force vector

F_net = ma

Newton’s Third Law

To every action, there is always an opposed but equal reaction

F_AB = F_-AB

v = ? (1-D Motion)

v = v₀ + at

x = ? (1-D Motion)

x = v₀t + at²/2

v² = ? (1-D Motion)

v² = v₀² + 2ax

F_g (Parallel) = ?

F_g (Parallel) = mg sin(θ)

Component of gravity parallel to the plane

Fg (Perpendicular) = ?

Fg (Perpendicular) = mg * cos(θ)

Centripetal Force

Involved in circular motion; Always points radially inward; Centripetal acceleration (and all acceleration) is always in the same direction as the net force

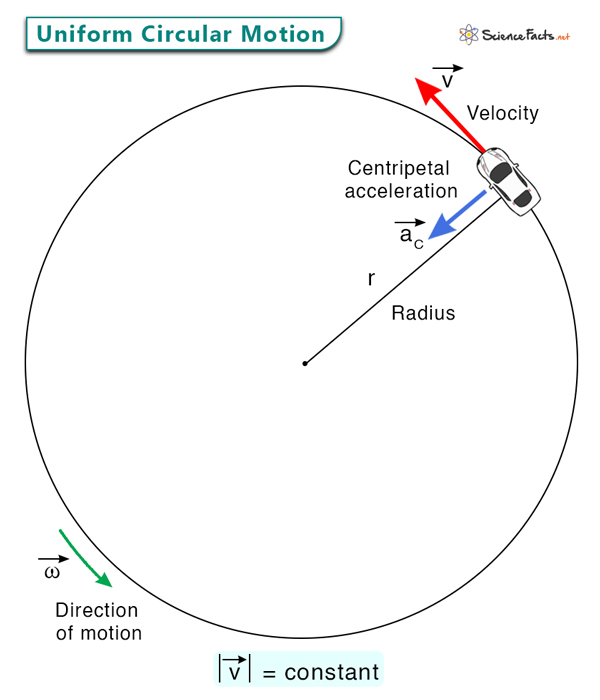
Magnitude of the Centripetal Force (F_c = ?)

F_c = mv²/r

Translational Equilibrium

Exists only when the vector sum of all of the forces acting on an object is zero; AKA First Condition of Equilibrium

Torque (Γ = ?)

Γ = r × F = rFsin(θ)

r = Length of the lever arm

F = Magnitude of the force

Γ = - = Clockwise rotation

Γ = + = Counterclockwise rotation

Rotational Equilibrum

Exists only when the vector sum of all the torques acting on an object is zero; AKA Second Condition of Equilibrium

Kinetic Energy (K = ?)

K = ½ * mv²

Gravitational Potential Energy (U = ?)

U = mgh

Elastic Potential Energy (U = ?)

U = ½ * kx²

k = Spring constant

x = Magnitude of displacement from equilibrium

Total Mechanical Energy (E = ?)

E = U + K

Conservative Forces

Forces that are path independent and that do not dissipate energy; Ex. Gravitational and electrostatic

Nonconservative Forces

When these forces are present, total mechanical energy is not conserved; Ex. Friction, air resistance, or viscous drag

Work (W = ?)

W = F * d = Fdcos(θ)

When something exerts forces on or against something else

Isobaric Work (W = ?)

W = P * ΔV

Power (P = ?)

P = W/t = ΔE/t

The rate at which energy is transferred from one system to another

Work-Energy Theorem (W_net = ?)

W_net = ΔK

The net work done by forces acting on an object will result in an equal change in the object’s KE

Mechanical Advantage (= ?)

Mechanical Advantage = F_out/F_in

The ratio of magnitudes of the forces exerted on an object by a simple machine (F_out) to the force actually on the simple machine (F_in)

Efficiency (= ?)

Efficiency = W_out/W_in = (load * load distance)/(effort * effort distance)

Use with pulleys

Kelvin to Celsius

K = C + 273

Fahrenheit to Celsius

F = (9/5 * C) + 32

Linear Expansion (ΔL = ?)

ΔL = αL∆T

Volumetric Expansion (∆V = ?)

∆V = βV∆T

β = 3α

Isolated Systems

Not capable of exchanging energy or matter with their surroundings

Closed Systems

Capable of exchanging energy, but not matter

Open Systems

Can exchange both matter and energy

State Functions

Independent of the path taken to get to a particular equilibrium state; Pressure, density, temperature, volume, enthalpy, internal energy, Gibbs free energy, entropy

Process Functions

Describe the path taken to get from one state to another; Work and heat

Change in Internal Energy (∆U = ?)

∆U = Q - W

• Isothermal: ∆U = 0, Q = W

• Adiabatic: Q = 0, ∆U = -W

• Isovolumetric: W = 0, ∆U = Q

Heat (q = ?)

q = mc∆T

q = mL

• L = Heat of transformation (phase change)

+ = Heat flows into system

- = Heat flows out of system

Conduction

Direct transfer of energy from molecule to molecule through molecular collisions; Must have direct physical contact between the objects

Convection

Transfer of heat by the physical motion of a fluid over a material; Only liquids and gases can transfer heat by this means

Radiation

Transfer of energy by electromagnetic waves

Change in Entropy (∆S = ?)

∆S = Q_rev/T

Q_rev = Heat gained or lost in a reversible process

Reversible Process

When the net change in the entropy of the system and its surroundings is zero; Process must go so slowly that the system is always in equilibrium and no energy is lost or dissipated

Weight from Density (F_g = ?)

F_g = ρVg

Specific Gravity (SG = ?)

SG = ρ/(1 g/cm³)

Pressure (P = ?)

P = F/A

Unit: Pa [1 Pa = 1 N/m²]

Absolute (Hydrostatic) Pressure (P = ?)

P = P₀ + ρgz

• P = Absolute pressure

  • P₀ = Incident pressure, pressure at the surface

Total pressure that is exerted on an object that is submerged in a fluid

Gauge Pressure (P_gauge = ?)

P_gauge = P - P_atm = (P₀ + ρgz) - P_atm

The difference between the absolute pressure inside the tire and the atmospheric pressure outside the tire

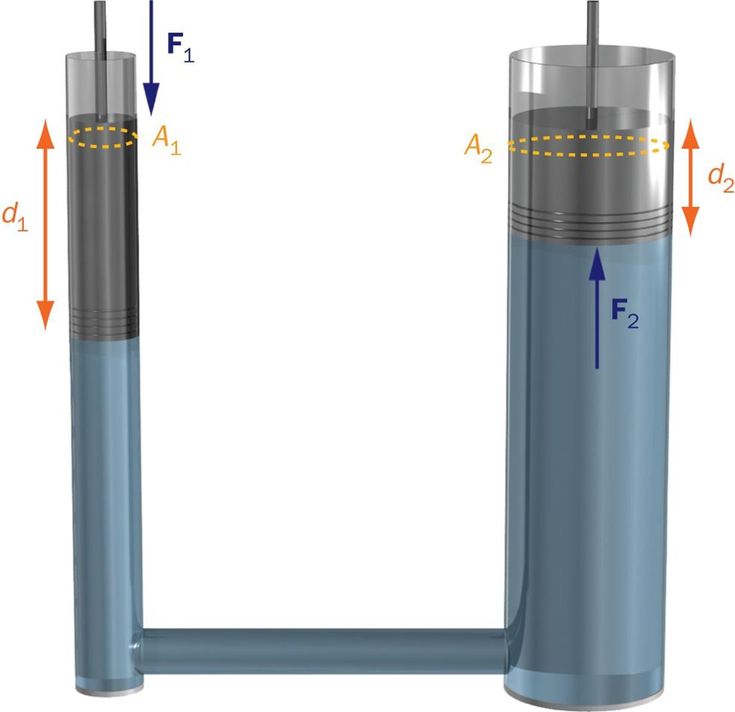
Pascal’s Principle (P = ?) (F₂ = ?)

P = F₁/F₂ = F₂/A₂

F₂ = F₁ * (A₂/A₁)

As A₂ is larger than A₁ by some factor, the magnitude of the force, F₂, exerted against A₂ must be greater than F₁ by the same factor so that P₁ = P₂

For fluids that are incompressible, a change in pressure will be transmitted undiminished to every portion of the fluid and to the walls of the containing vessel

Buoyant Force

F_buoy = ρ_fluidV_{fluid displaced}g = ρ_fluidV_submergedg

If two objects placed in a fluid displace the same volume of fluid, they will experience the same magnitude of buoyant force even if the objects themselves have different masses

An object will float, no matter what it is made of and no matter how much mass it has, if its average density is less than or equal to the density of the fluid into which it is placed

Viscosity (η)

The resistance of a fluid to flow

Unit: Pascal-second [Pa * s = N * s/m²]

Pouiseuille’s Law (Q = ?)

Q = (πr⁴∆P)/8ηL)

• Q = Flow rate

• r = Radius of the tube

• ∆P = Pressure gradient

• η = Viscosity of the fluid

• L = Length of the pipe

Critical Speed (v_c = ?)

v_c = N_Rη/ρD

• N_R = Reynolds number

In unobstructed fluid flow, turbulence can arise when the speed of the fluid exceeds this

Linear Speed (Q = ?)

A measure of the linear displacement of fluid particles in a given amount of time; While flow rate is constant, ______ of the fluid does change relative to the cross-sectional area

Q = v₁A₁ = v₂A₂

Continuity Equation: Shows that fluids will flow more quickly through narrow passages and more slowly through wider ones

Bernoulli’s Equation

P₁ + (1/2)ρv_1² + ρgh₁ = P₂ + (1/2)ρv₂² + ρgh₂

h = height of the fluid above some datum

More energy dedicated toward fluid movement means less energy dedicated toward static fluid pressure, and vice versa

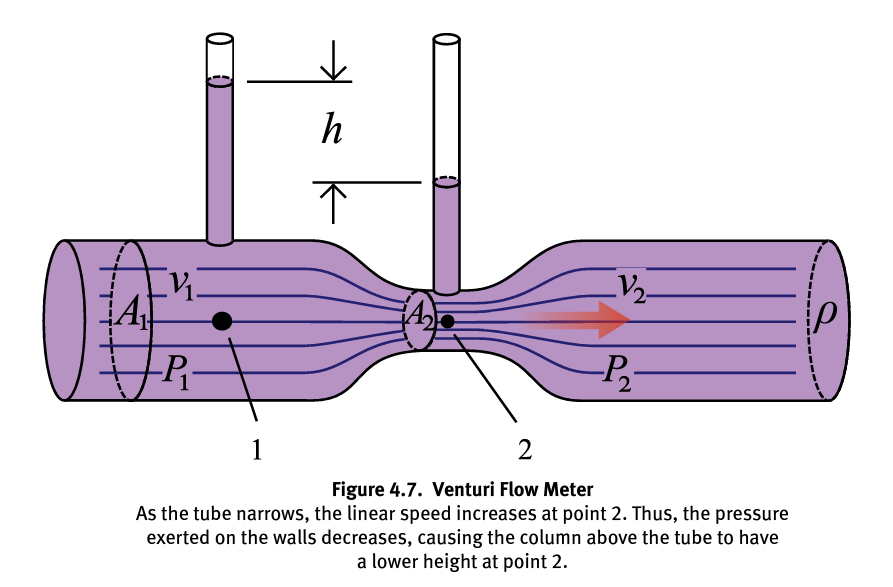
Venturi Effect

With lower absolute pressure, the column of fluid sticking up from the Venturi tube will be lower and point 2; As the tube narrows, the linear speed increases at point 2. Thus, the pressure exerted on the walls decreases, causing the column above the tube to have a lower height at point 2.

Circulatory system

A closed loop that has a nonconstant flow rate that can be measured as a pulse

• Blood volume entering the heart is always equal to blood volume leaving the heart during a single cycle

• As blood flows away from the heart, each vessel has a progressively higher resistance until the capillaries; however, the total resistance of the system decreases because the increased number of vessels are in parallel with each other

• Return flow to the heart is facilitated by mechanical squeezing of the skeletal muscles, which increases pressure in the limbs and pushes blood to the heart, and the expansion of the heart, which increases pressure in the limbs and pushes blood to the heart, and the expansion of the heart, which decreases pressure in the heart and pulls blood in

• Venous circulation holds approximately three times as much blood as arterial circulation

Charge

Unit: Coulomb, e = 1.60 × 10^-19 C

Insulator

Will not easily distribute a charge over its surface and will not transfer that charge to another neutral object very well

Conductor

If given a charge, the charges will distribute approximately evenly upon the surface of the ____; Able to transfer and transport charges

Coulomb’s Law (F_e = ?)

F_e = kq₁q₂/r²

k = Coulomb’s Constant

Quantifies the magnitude of the electrostatic force F_e

Magnitude of an Electric Field (E = ?)

E = F_e/q = kQ/r²

F_e = The magnitude of the force felt by the test charge 1

Q = Source charge magnitude

Electric Potential Energy (U = ?)

U = kQq/r

∆U = W

Electric Potential (V = ?)

V = U/q = kQ/r

Potential Difference (Voltage) (∆V = ?)

∆V = V_b - V_a = W_ab/q

W_ab = Work needed to move a test charge q through an electric field from point a to point b. For a positive test charge, this means moving from a position of higher electric potential to a position of lower electric potential. A negative test charge will spontaneously move from a position of lower electric potential to a position of higher electric potential.

Positive charges will spontaneously move in the direction that decreases their electric potential (negative voltage), whereas negative charges will spontaneously move in the direction that increases their electric potential (positive voltage)—yet, in both cases, the electric potential energy is decreasing.

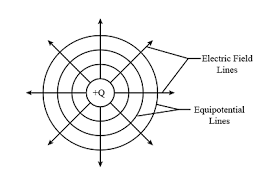
Equipotential Line

A line on which the potential at every point is the same. That is, the potential difference between any two points on an equipotential line is zero. No work is done when moving a test charge q from one point on an equipotential line to another.

Electric Dipole (V = ?)

V = (kqd/r²)cosθ

Results from two equal and opposite charges being separated a small distance d from each other, can be transient or permanent

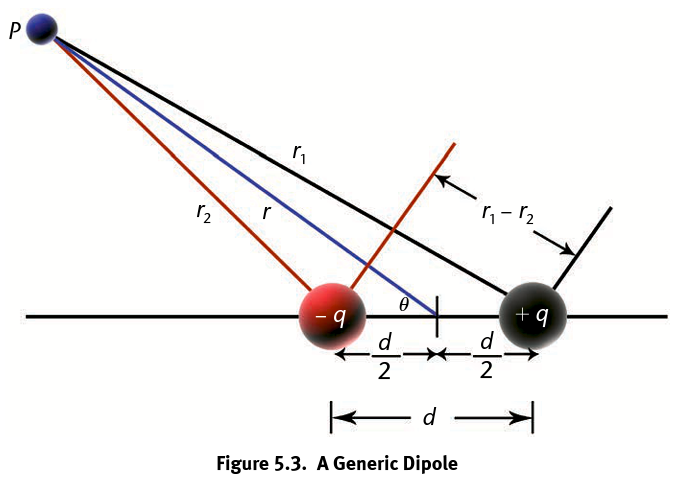
Dipole Moment (p = ?)

p = qd

The product of charge and separation distance

Units: C * m

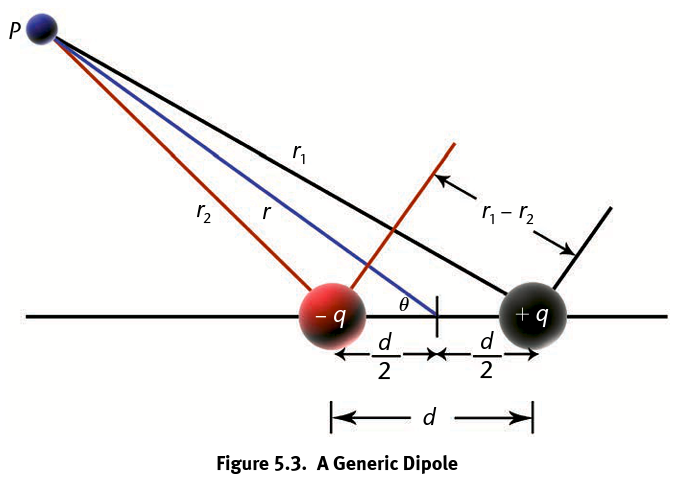
Perpendicular Bisector of the Dipole (E = ?)

E = (1/(4π∈₀)) * p/r³

The plane that lies halfway between +q and -q. Because the angle between this plane and the dipole axis is 90° (and cos 90° = 0), the electric potential at any point along this plane is 0. The electric field vectors at the points along the _______ will point in the direction opposite to p.

Net Torque on a Dipole (τ = ?)

τ = pEsinθ

• p = Magnitude of the dipole moment (p = qd)

• E = magnitude of the uniform external electric field

• θ = Angle the dipole moment makes with the electric field

Diamagnetic Materials

Made of atoms with no unpaired electrons and that have no net magnetic field; Slightly repelled by a magnet and so can be called weakly antimagnetic

Paramagnetic Materials

Has unpaired electrons and a net magnetic dipole moment; Will become weakly magnetized in the presence of an external magnetic field, aligning the magnetic dipoles of the material with the external field

Ferromagnetic Materials

Have unpaired electrons, so these atoms do have a net magnetic dipole moment; Have permanent atomic magnetic dipoles that are normally oriented randomly so that the material has no net magnetic dipole; Become strongly magnetized when exposed to a magnetic field or under certain temperatures

Magnitude of the Magnetic Field (B = ?)

B = μ₀I/2πr

Magnitude of the magnetic field produced by the current I in the wire at a perpendicular distance, r, from the wire

μ₀ = Permeability of Free Space

B = μ₀I/2r

Magnitude of the magnetic field at the center of a circular loop of current-carrying wire of radius r

Magnetic Force (F_B = ?)

F_B = qvBsinθ

F_B = ILBsinθ

Magnitude of the force created by an external magnetic field where I is the current, L is the length of the wire in the field, B is the magnitude of the magnetic field, and θ is the angle between L and B