unit 4: waves

oscillations

oscillations

any vibration that goes back and forth without an overall resultant displacement

describing oscillations — displacement (x)

the distance the particle has moved from its rest position (equilibrium)

describing oscillations — amplitude (A)

the maximum distance that a particle moves from its rest position (this is a scalar!)

describing oscillations — frequency (f)

he number of oscillations per second or the number of waves to pass a point every second (also a scalar because of time), f=1/T

describing oscillations — period (T)

the time it takes for an oscillating particle to complete an oscillation or the time for a wave to move through one complete wavelength

graphing oscillations

• on a sine wave, movement would continue infinitely without friction

• sine waves come from circular motion looking at vertical or horizontal displacement from a point on the circumference of the circle

• time on the x axis, displacement on the y axis

• the length between repeating parts of the sine wave is the time period, direction matters in this eg. from halfway going up the time period would need to be measured until it hits the line going up again (not the first point where it would be going in the other direction)

• amplitude on the wave is symmetrical on the horizontal access and the space between the extremes and the x axis

relating displacement, velocity and acceleration in SHM

• velocity is the derivative of displacement

• acceleration is the derivative of velocity, the derivative of the derivative of displacement

• displacement cannot be represented as a derivative but it is the anti derivative of velocity (the integral)

• displacement lags T/4 behind velocity, 3T/4 ahead (out of phase by…)

• velocity lags T/4 behind acceleration, 3T/4 ahead

• displacement lags T/2 behind acceleration (can go either way as it is in the middle)

conditions for SHM

• There is a fixed cyclical path.

• There is a central equilibrium point.

• The motion repeats at equal time periods (periodic).

• Displacement, velocity, and acceleration change continuously.

• There is a restoring force directed toward the equilibrium point.

definition of SHM

• motion arising from acceleration of an object that is proportional to its displacement from a fixed equilibrium point (rest position) and directed toward that point.

• motion arising from a linear restoring force directed to a fixed equilibrium point

what does a phase shift do?

Two sinusoidal curves of equal period have a phase shift that translates one curve relative to the other in time, expressed as a fraction of a cycle, or as an angle in radians or degrees

travelling wave

a disturbance that propagates (transmits) energy without transferring physical material (a medium)

mechanical wave

A mechanical wave propagates its disturbance through a medium by an oscillating movement of the particles in the medium

transverse wave

particles of the medium oscillate perpendicular to the direction of the wave and propagation of energy.

longitudinal wave

the particles of the medium oscillate parallel to the direction of the wave, the wave and oscillations follow the same direction

electromagnetic wave

propagates as a transverse wave through a medium or a vacuum by oscillations of coupled, time-varying electric and magnetic fields

how is wave length measured?

• wavelength (λ) is measured in metres as is amplitude (A)

• wavelength is peak to peak while amplitude is vertical from the x axis to the peak

definition of a ray

• the line showing the direction in which a wave transfers energy

  • direction of propagation, the two are parallel

  • perpendicular to the wave front

definition of a wave front

• the surface that travels with a wave and is perpendicular to the direction in which the wave travels (the ray)

  • the lines that are perpendicular to the ray

  • parallel to the direction of propagation

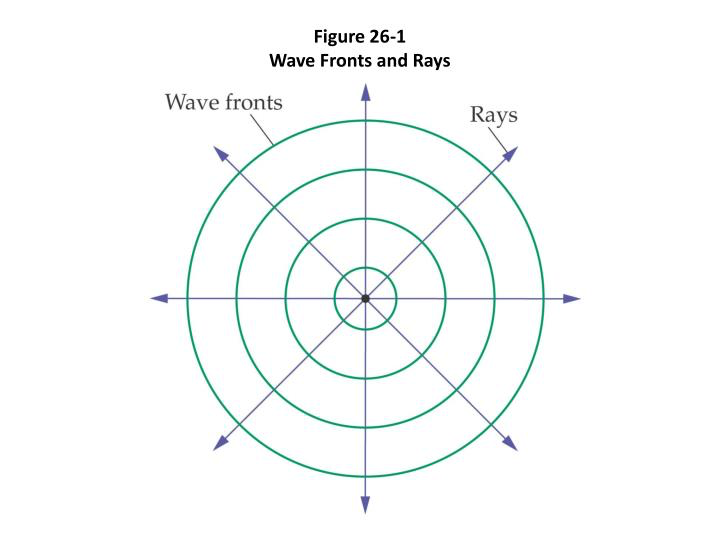
wave fronts and rays from a point sources

• this diagram shows a point source so makes waves that propagate away from the point, making the wave fronts circles

• the rays are parallel to the tangent of the circle — if you zoomed in enough the curve would look flat

• the rays can be perpendicular to the wave front as the tangent will always be a straight line

superposition

• the resultant displacement at any point is the sum of the seperate displacements due to the two waves

  • the way we add waves, like dealing with vectors

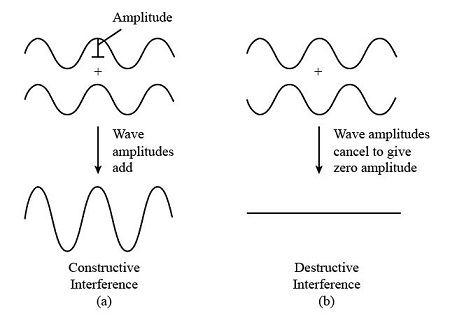
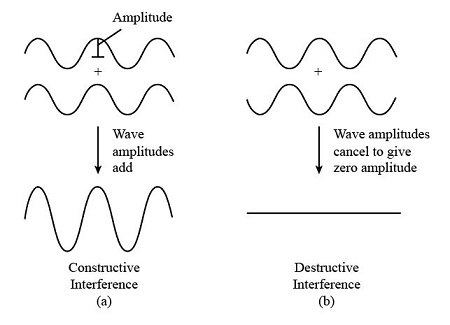
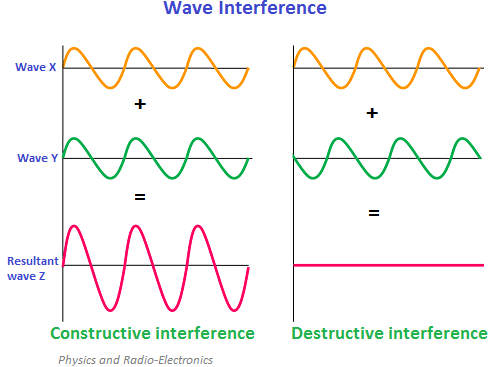
constructive interference

constructive interference is when the waves are in phase so the amplitudes add together to produce a stronger signal

destructive interference

destructive interference is when the waves are out of phase so the amplitudes cancel each other out

conditions for interference

• only the amplitude can change if the waves have the same frequency, speed and wave length

• the waves only cancel out completely is the amplitudes are the same

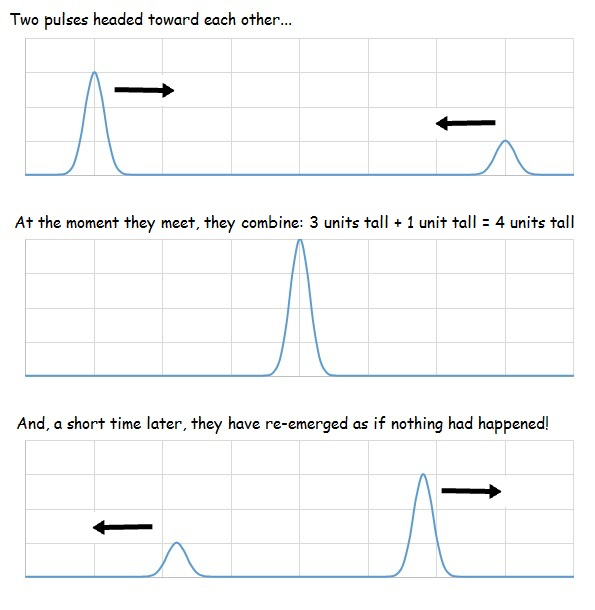
• when two pulses meet they instantaneously become one and then continue as before having crossed over, this behaviour is different to particle collisions as the pulses do not join or rebound

intensity

• intensity — the rate of energy transmitted (power) per unit area at right angles to the wave velocity

  • is proportional to the amplitude squared so doubling the amplitude will quadruple the intensity

  • measured in watts per square metre (Wm^-2)

• energy is also proportional to the amplitude squared

polarisation of light

• a polarised lens contains many long chains of molecules

• after going through a polariser the amplitude of oscillations is diminished

critical angle

the smallest angle at which there is total internal reflection, the refractive angle is 90º

optical density

• high to low optical density = away from the normal

• low to high optical density = towards the normal

• optical density has nothing to do with actual density, instead it is related to the refractive index

• the refractive index of water is about 1.33

• hot air and cold air have different refractive indexes

sine of a critical engle

the sine of the critical angle is n2/n1 so long as n2>n1 since the sine of any angle must be between -1 and 1

condition for total internal reflection

if the incident angle is greater than the critical angle there is total internal reflection such that the light goes like a mirror on the normal

how pulses collide

• principle of superposition applies

• when they overlap they add together

• once they pass through each other they continue as if nothing happened

wave interference

• waves of different frequencies can be added

• any waves that are the same type (eg. both sound) can be added

phase of waves

• sine waves can be shown using a reference circle so can be referred to as an angle, this is the phase

completely out of phase (anti-phase)

• the phase difference between the crests and valleys is pi which is referred to as completely out of phase

• if waves that are completely out of phase meet the resultant displacement is zero

• on a circle this is two points that are opposite each other showing the diameter of the circle

• a phase difference of pi is also the distance of wave length/2

path difference

• a whole number path difference results in a phase difference of 0º so constructive interference occurs

• if the path difference is half a wave length away from being a whole number (eg. 121/2(λ)) the phase difference is pi so destructive interference occurs

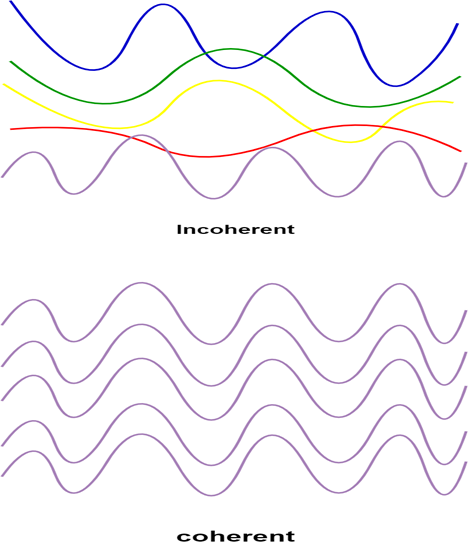
coherent waves

• coherent waves have a constant phase difference which can be anything so long as its constant

• coherent waves also have the same frequency however not all waves with the same frequency will be coherent

interference with coherent waves

• two coherent sources of light will produce interference

• when the path difference is an integer number of wave lengths (whole number) the interference will be constructive

destructive interference of coherent waves

• a path difference of half a wave length will create maximum destructive interference

Huygen’s principle

• Huygen’s principle — every point in a wave front is a point source of the wave

• point source — a place in space which is an origin of waves

wave length definition

• the distance between the wavefronts is the wavelength

• the wavefronts are put at the peaks of the wave

• the troughs are half way between the wavefronts assuming the waves are in SHM (are sinusoidal)

what is the energy in a wave proportional to?

the energy in a wave is proportional to the square of the wave’s amplitude

is the rate of energy transfer by waves constant?

• straight waves in a uniform medium do not change wavelength or speed or direction or shape so the rate of energy transfer is also constant

• for circular waves the amount of energy is constant along the wavefronts however it is distributed evenly so for the circumference of the wave front there is less energy the further from the point source it is measured, this is why amplitude decreases with distance for a circular wave

which waves can be polarised?

transverse waves

how is light polarised?

• by going through a polariser

  • with an analyser perpendicular to the polariser no light is observed at the end

  • light must pass through thin molecular chains

• reflecting light from a smooth surface

  • all light reflected from a smooth non-metallic surface is partially polarised

  • at a particular angle of incident (Brewster’s angle) on smooth insulators the light will be fully polarised

  • this is how polarising sunglasses work

Malus’ law

he relationship between intensity and the incident angle is not linear — the intensity of the unpolarised light entering the polariser must be twice the intensity of the polarised light leaving the polariser

small angle approximation (in radians!)

• sinθ=0

• cosθ=1

• tanθ=0

standing wave definition

A standing wave (or stationary wave) is a wave in a medium in which each point on the wave axis has an associated constant amplitude – all points move coherently – and there is no transport of energy. 

nodes on standing waves

The locations of zero amplitude are called nodes, and the locations of maximum amplitude are called anti-nodes. Adjacent nodes are separated by λ/2, where λ is the wavelength.

resonance

the situation in which an external driver oscillating at a system's natural frequency transfers energy into the system, which in this case is the standing wave.