geometry unit6 6.1-6.3

Concurrency

When 3-or more lines, rays or segments intersect at the same point

Circumcenter Theorem

The circumcenter of a triangle is equidistant from the vertices of the triangle.

Angle Bisector Theorem

If a point lies on the bisector of an angle. then it is equidistant from the two sides of the angle

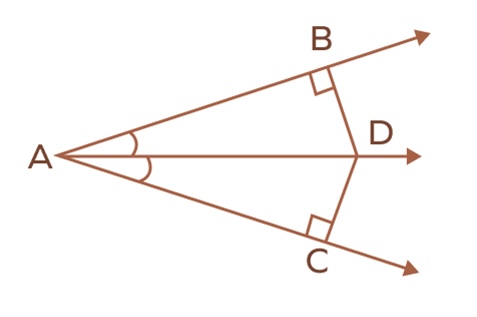
Converse of the Angle Bisector Theorem

If a point is in the interior of an angle and is equidistant from the two sides of the angle, then it lies on the bisector of the angle.

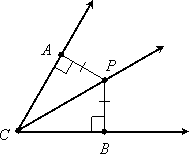
Perpendicular Bisector Theorem

In a plane. if a point lies on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment.

If CP is the angle bisector of AB, then CA = CB.

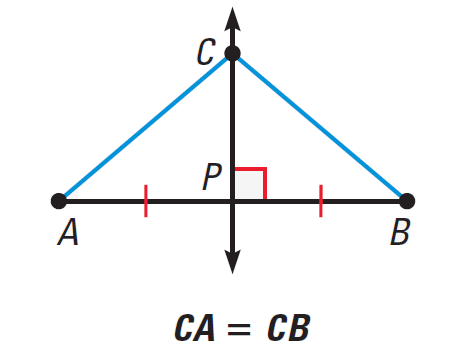
Converse of the Perpendicular Bisector Theorem

In a plane, if a point is equidistant from the endpoints of a segment, then it lies on the perpendicular bisector of the segment.

Definition of incenter

The angle bisectors of a triangle are concurrent. This point of concurrency is the incenter of the triangle.

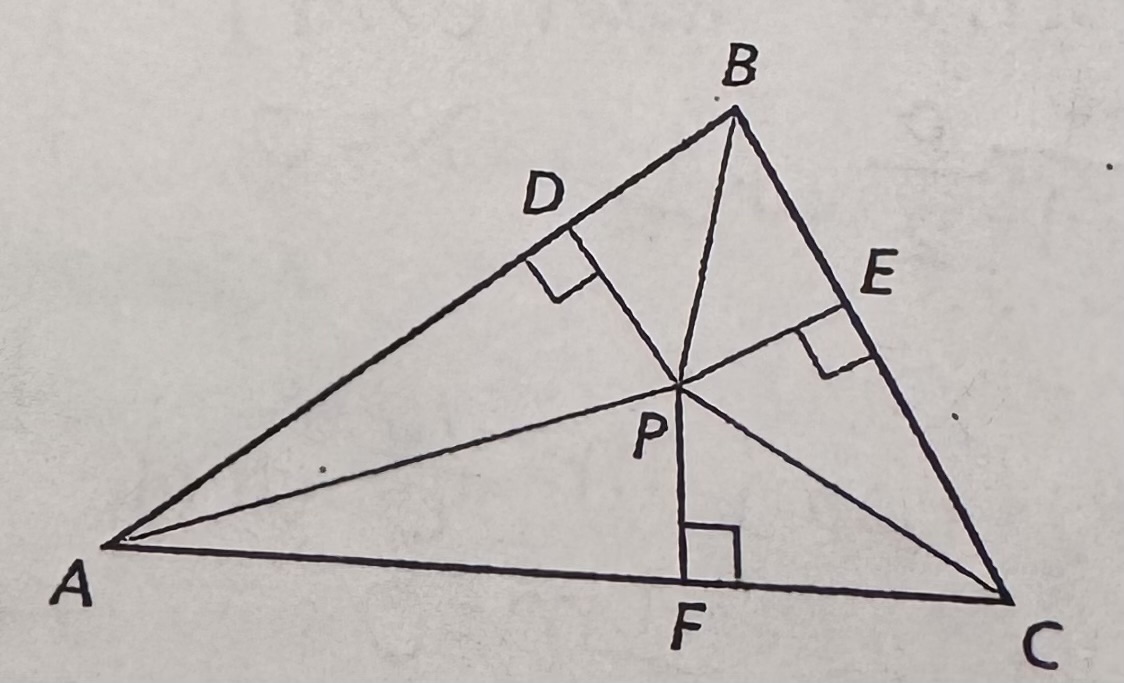
Incenter Theorem

The incenter of a triangle is equidistant from the sides of the triangle.

If AP, BP, and CP are angle bisectors of

ABC, then PD = PE=PF.

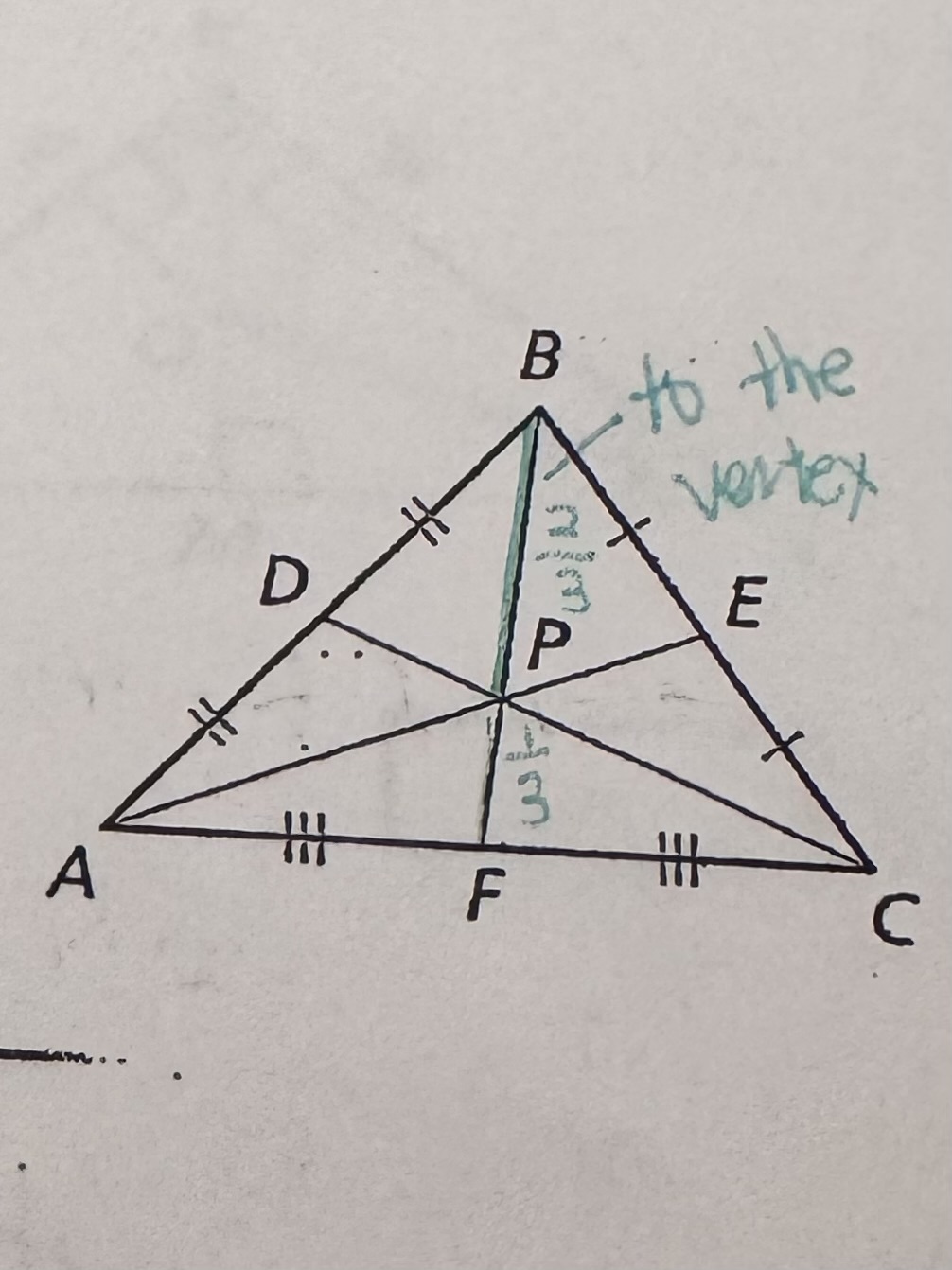
Centroid Theorem

The centroid of a triangle is two-thirds of the distance from each vertex to the midpoint of the opposite side.

Median

segment from the vertex to the midpoint of the opposite side.

Orthocenter on the triangle

Right angle

Orthocenter inside the triangle

Acute triangle

Orthocenter outside the triangle

Obtuse triangle

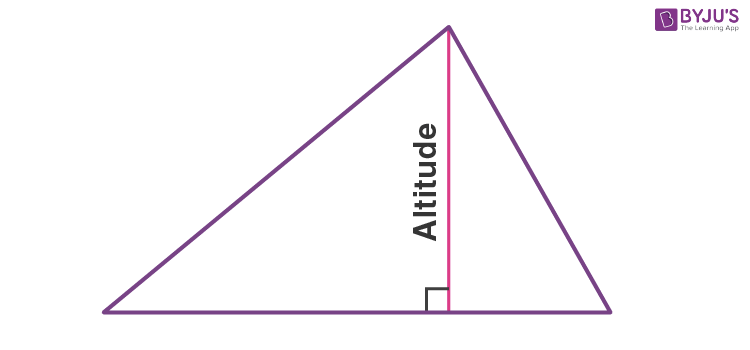
Orthocenter

The lines containing the altitudes of a triangle are concurrent. This point of concurrency is the orthocenter of the triangle.

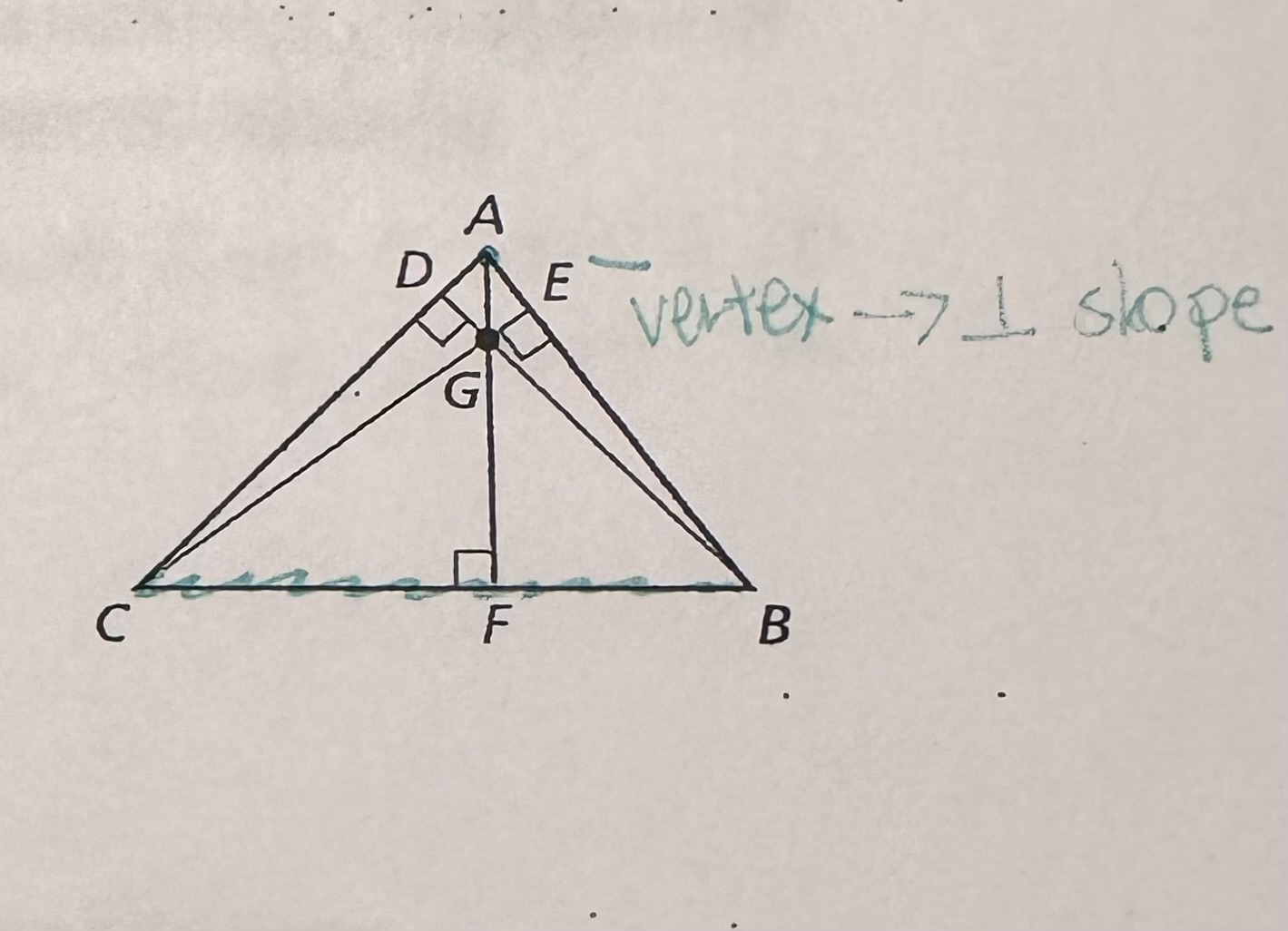
Altitude

a line segment from a vertex drawn perpendicular (at a 90° angle) to the opposite side