psyc 2100wq exam 1

exam 1 lecture notes

empirical science

observation based and numerically observed science

construct

thing to be observed

must be defined before numerical observation

“what” is observed

operationalization

identification of measurement procedure for measuring external behavior — then uses resulting measurements as definition and measure of a hypothetical construct

“how” something is observed

variable

characteristic or condition that changes or has different values for different individuals

determined and declared after observation

cannot be considered a variable unless observed to show variation

covariation

the variation of one thing - shown to be related to the variation of another thing

simple covariation

non-ordered — absence of specified order in reference to 2 variables that vary together

ordered covariation

order of covariation is specified

shows causality

done only by manipulation and shown IV/DV relationship — experimental

data

numerically recorded observations

Hypothesis

formal statement of what a researcher believes is true

declared in a written/verbal statement to the public

experimental group

receives treatment/manipulation

control group

does not receive treatment/manipulation

causality

assume variation that occurs due to or as a result of cause and effect

1-1 causality

for every cause there is an effect

chain of cause and effect (cause and effect links)

C1—> E1 (becomes c2) —>E2 etc.

simple covariation diagram

V1 ←→V2

ordered covariation diagram

V1 →V2 or V1 ←V2

mutually exclusive, only 1 can occur at one time

confound variable/third variable

only determined under ordered covariation

3rd variable that may be the cause of both or either V1 or V2

statistic

set of mathematical procedures for organizing, summarizing and interpreting information and numerically numbered observations

percent

0-100

frequency

0-infinity (highest number possible

proportion

0 -1.00

descriptive statistics

used to describe the sample measured

inferential statistics

used to draw inferences/predictions about the population (can be applied to generalize)

Population

unspecified N number of individuals for which we have numeric observations

only exists bc theorized to exist

sample

specified/known number of individuals from population

skewed

line drawn over distribution is not a bell shape

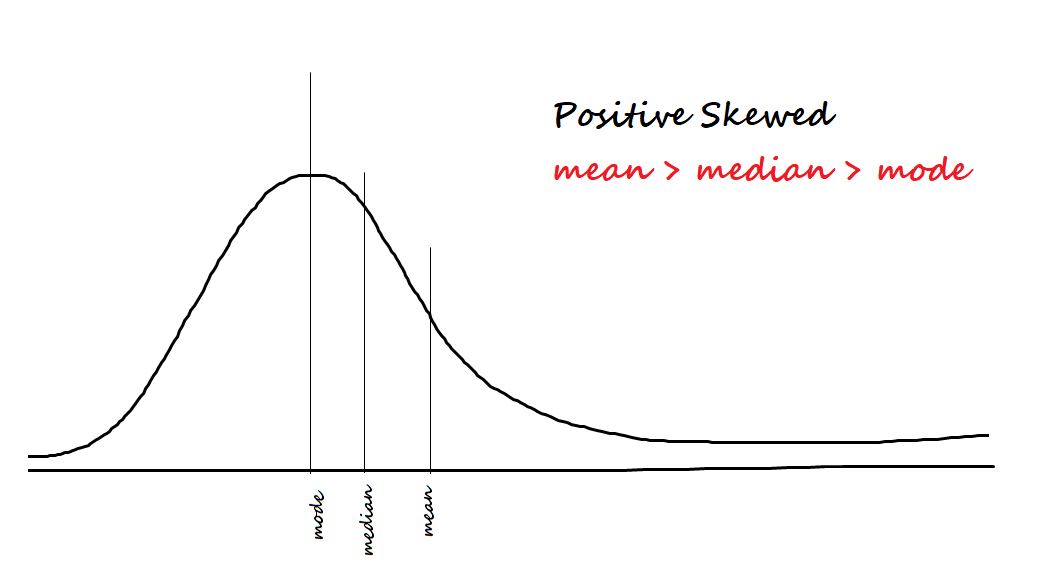
positive skewed

tail falls on positive side (the right) and high frequency on the left

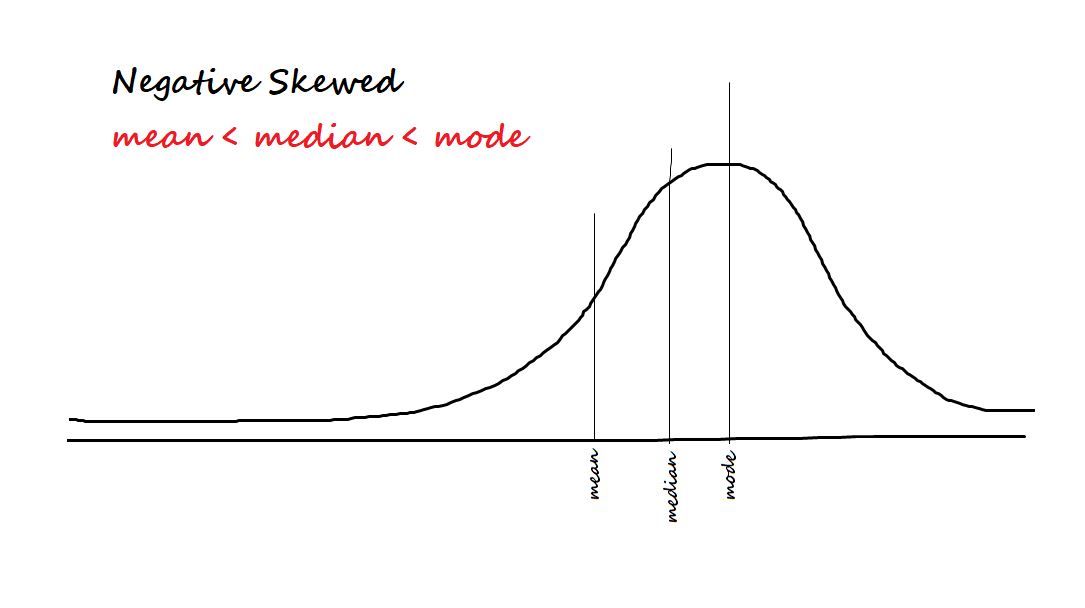
negative skewed

tail falls on the negative side (the left) and high frequency of scores on the right

frequency distribution

visual of low to high scores — all scores fall under the line

bell shaped distribution

scores in the middle show highest frequency then trail off along both sides

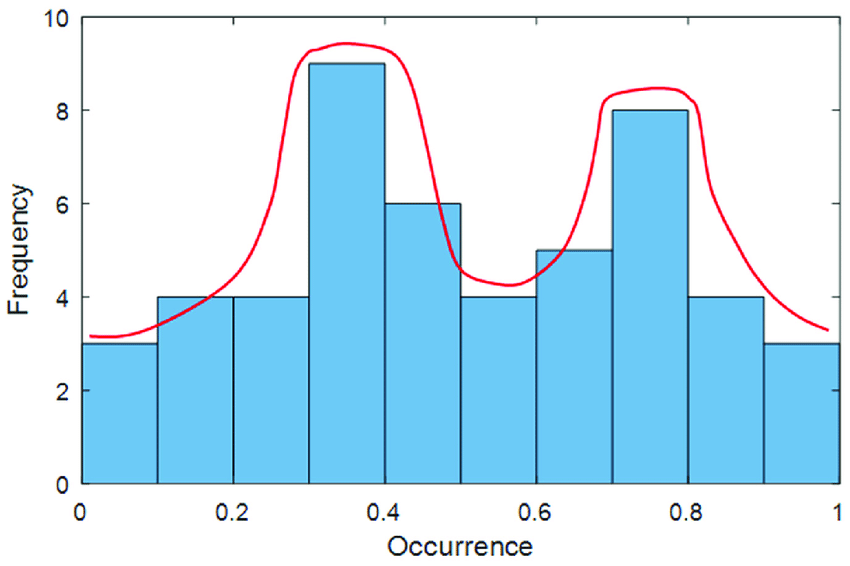
bimodal distribution

contains 2 peaks

best when use 2 modes to describe this data

population parameter

value that describes a population, usually derived from measurements from individuals in the population

sample statistic

value that describes a sample

mean for population (parameter)

μ_x=∑x/∞

we can theorize this exists but cannot actually numerically represent it

Mean for sample (statistic)

x̄= ∑x/N

can be used as an inference about the population

median (Md)

used when there is skewed distribution or presence of outliers

the number that falls directly in the center of the distribution of scores

mode(Mo)

score in distribution that occurs with the highest frequency

done with bimodal data or nominal data

central tendency

representation of where scores tend to show highest frequency

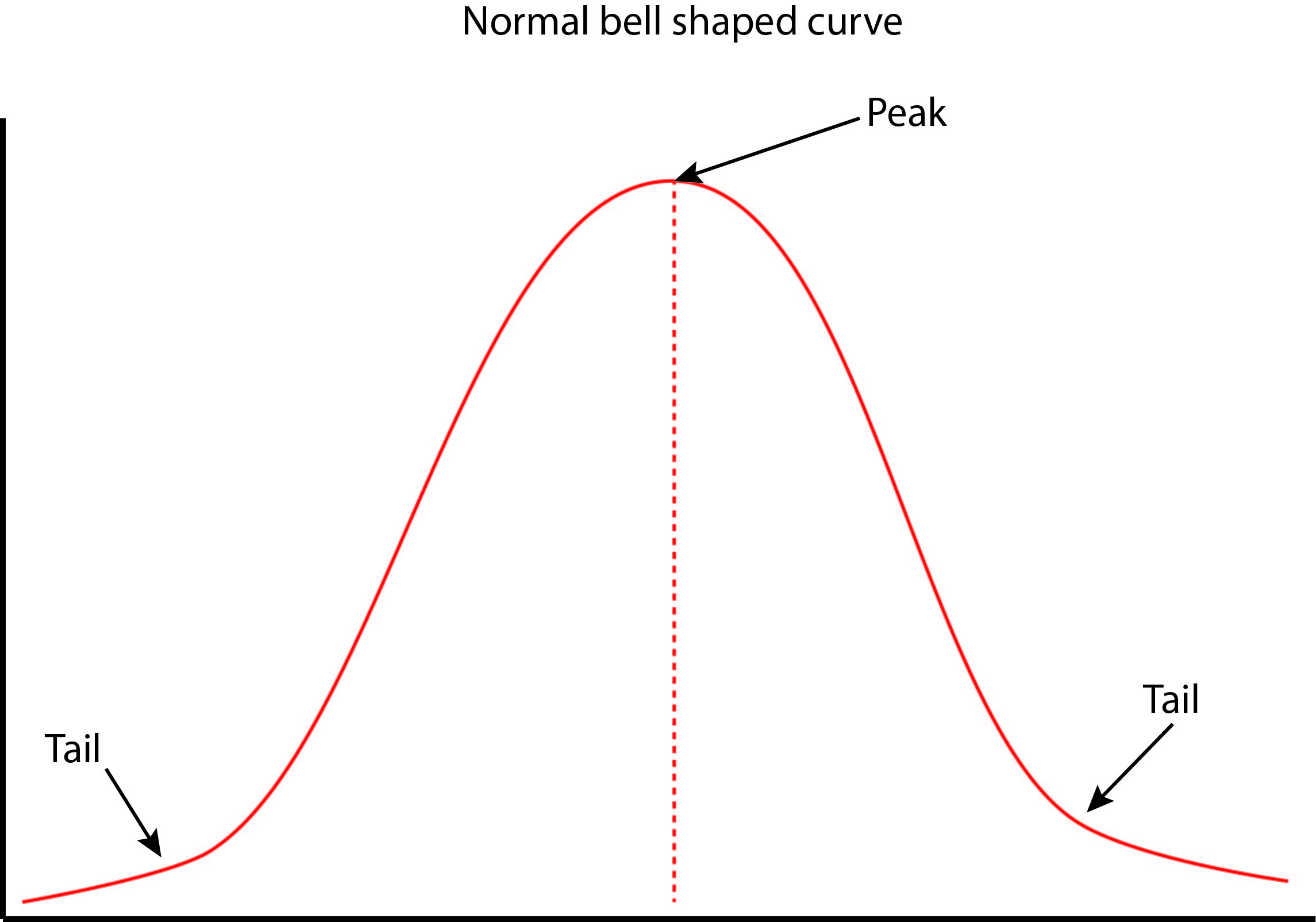
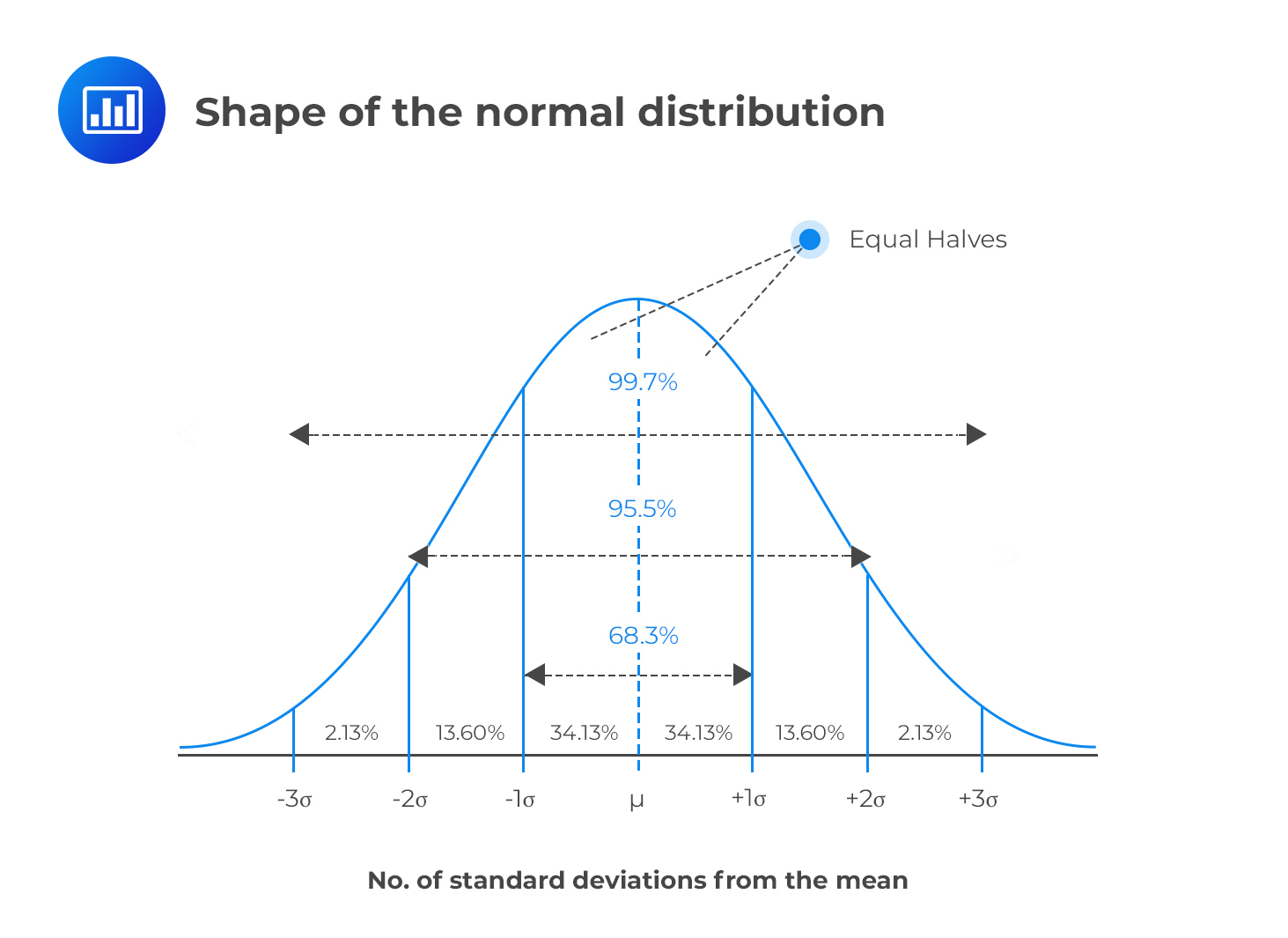
normal distribution

bell shaped curve

mean, median and mode are all the same number

show symmetry — proportion of scores on both sides of the central tendencies is .50

standard deviation

indicates variation of scores in a distribution

amount on average the scores deviate from the mean

high standard deviation

more on average that scores deviate from the mean

low standard deviation

less on average that scores deviate from the mean (clustered together)

standard deviation equation (for sample)

S= √ (∑(x-x̄)²/n-1)

Standard deviation equation (for population)

S= √ (∑(x-x̄)²/N)

variance equation

Variance = (∑(x-x̄)²/n) NO SQUARE ROOT)

what does the equation for standard deviation mean

the square root of the sum of squared deviations (or deviations squared) over the number summed

normal distribution frequency

from -1s to 1s = .683

from -2s to 2s = .955

from -3s to 3s =.997

frequency distribution table

x	f	%	P
1 (female)	30	60%	.60
0 (male)	20	40%	.40

simple covariation hypothesis example

self esteem is related to academic success

ordered covariation hypothesis example

self esteem training (IV) leads to academic success (DV)

design of a study

must be indicated before data is collected

determines how the data is to be collected (procedures)

types of designs

experimental versus non-experimental

chosen based off of whether hypothesis is ordered or simple

case study

non-experimental design

observes 1 individual

used often when permission to observe someone is difficult to obtain

naturalistic observation

setting in which variation naturally occurs + can be observed

ex. observation of birds

trial

indicates and specifies where and when the data are going to be collected and how many trials will be done

lab environment

can control variation of everything except for the one thing you are manipulating to vary

experimental design

ordered covariation is used

one variable is manipulated while others are observed in relation to that manipulated variable

shows IV, DV relationship

can determine cause and effect

ex. mechanical birds head bop study

skepticism

the suggestion of doubt about a claim of what is true (a knowledge claim)

always present in science bc knowledge claims are never absolute

threat to validity of study (rectify by adjusting or building a design to fit)

validity of design

basis by which a claim is made sufficient and reasonable

is the design of the study sufficient for providing empirical basis of knowledge claim

external validity

does the IV-DV relationship as observed in the study generalize beyond the study to other settings, people or other points in time

ex. bird study did not address female female interactions — perhaps specific to “like-gender“ interactions not just male-male interactions)

internal validity

did the IV really cause variation in the DV or is the variation due to something else

ex. adding control group to SE study bc possibly AS affected by attention given not just the actual content of SE training — give control group 90 minutes of attention unrelated to SE

measurement

aka measure, scale, test

used to assign numbers to observations

used to operationalize how numbers are assigned to operations — record numeric operations

psychometrics

generation of criteria to evaluate goodness of a measure

Reliability (in reference to measurement and in reference to scores yielded)

consistency — do the scores yielded by the scale show consistency

over time, over different measures of scale or over responses of individuals to the measures

validity (in reference to measures and scores yielded by measures)

accuracy — do the scores yielded by the scale give a correct representations of the “low-high” variation of the variable of interest

covariation

can be used to indicate consistency /reliability

pearson product moment correlation coefficient

measures the degree and direction of the linear relationship between 2 variables

=r

done on a -1 to 1 scale

r=.00

the grounding point

absence of covariation in data

allows for show of HOW MUCH covariation there is

1,2,3

1= departure from 0 shows there is covariation present in the data

2= if more than 0 — there is positive covariation, if less than 0 — there is a negative correlation

3= HOW MUCH positive or negative covariation is present

test-retest design (reliability)

can examine consistency of scores over time

ex. test same individuals at 2 separate times, (t1 and t2) — if scores show consistency across time — the measure is reliable

equivalent/parallel forms design (reliability)

consistency of scores across different scaling formats

ex. individuals self-report SE on 5 item scale ranking system + same individuals show the same/consistency in scores when done in interview format with a scorer of the same 5 item ranked scale.

inter-item reliability design (internal consistency design)

consistency of responses to items on the scale

ex. amount on average of consistency of covariation in respect to all possible pairs of items

use of inter-item correlation matrix

r̄

the average of coefficients

cronbach’s alpha is roughly equal to this

r̄=∑x/N

correlation matrix

scores yielded by scale

provides a correct representation of low-high variation of variable of interest

predictive criterion-related design (validity)

accuracy of scores yielded by scale showing a predictor —> criterion relationship

ex. self estreem measured at time one predicts academic success measured at time two — measured at 2 different times to see if SE is a predictor for AS (criterion)

coupling hypothesis

used to show multiple hypotheses

H1 — SE is related to AS

H2 — SE at T1 predicts AS at T2

convergent-discriminant validity design

convergent — the ones you think do show covariation and relate

discriminant— something that could be related but when shows no covariation between 2 other items shows accuracy of measuring the thing your’re intending to measure and not something else

ex. H1 — SE is related to AS but is not related to optimism — convergent coefficient (SE + AS show r=.60) versus discriminant coefficient (SE + OPT show r= .05)

covariance

used to derive correlation coefficient (r)

the average of how deviations scores of x relate to deviation scores of Y

covariance equation

COV = ∑(x-x̄)(y-ȳ)/n-1

coefficient derived from covariance equation

r= COV_x(y)/(Sd_x)(Sd_y)

why do we use pearson’s coefficient

because of the underlying metric of -1 to 1 — allows indication of how much correlation/covariation there is

what does pearson’s correlation do

indicates linear relationsip amount (from a straight line) and the slope of that line

linear

in reference to a straight line

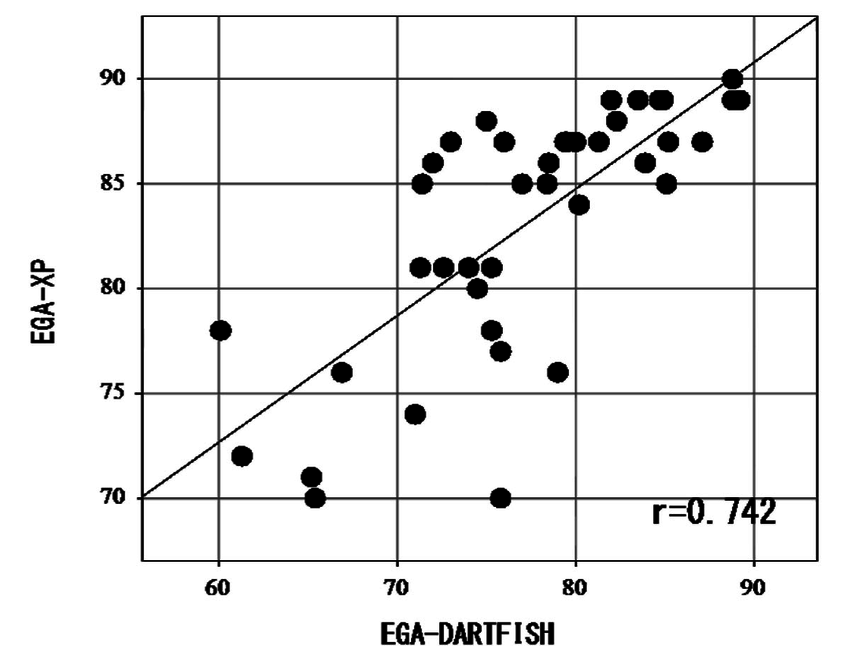
bivariate scatter plot

two variables measured and plotted in a scatterplot

Line of best fit

given scatter plot of all points of individuals — straight line closest to all possible points that is better than any other line

undefined/ideterminate

coefficient does not exist because one variable does not have variation — need variation for both in order to have a coefficent

class rule !

before interpretting a coefficient — plot the data

moderate positive correlation

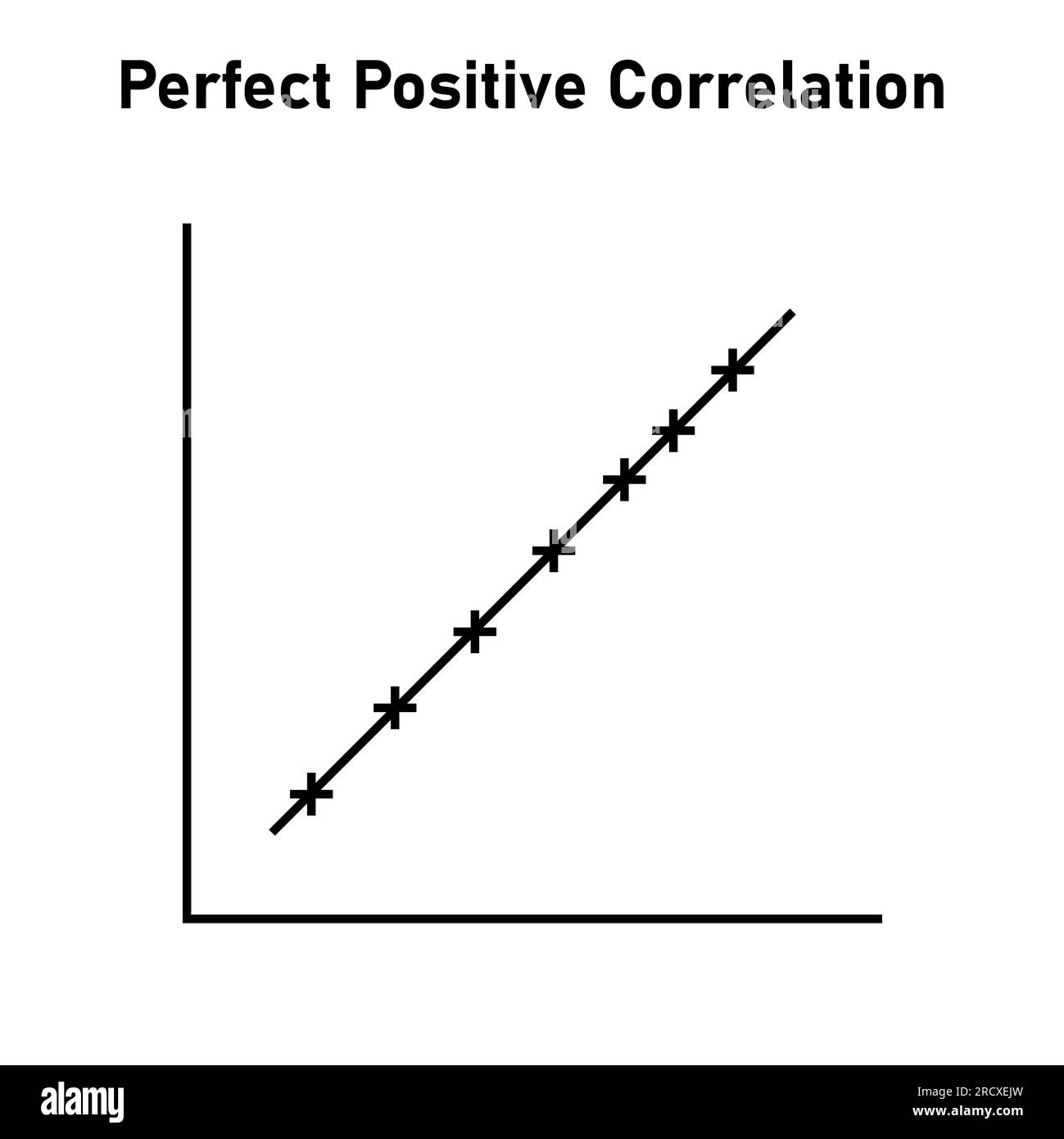
perfect positive correlation

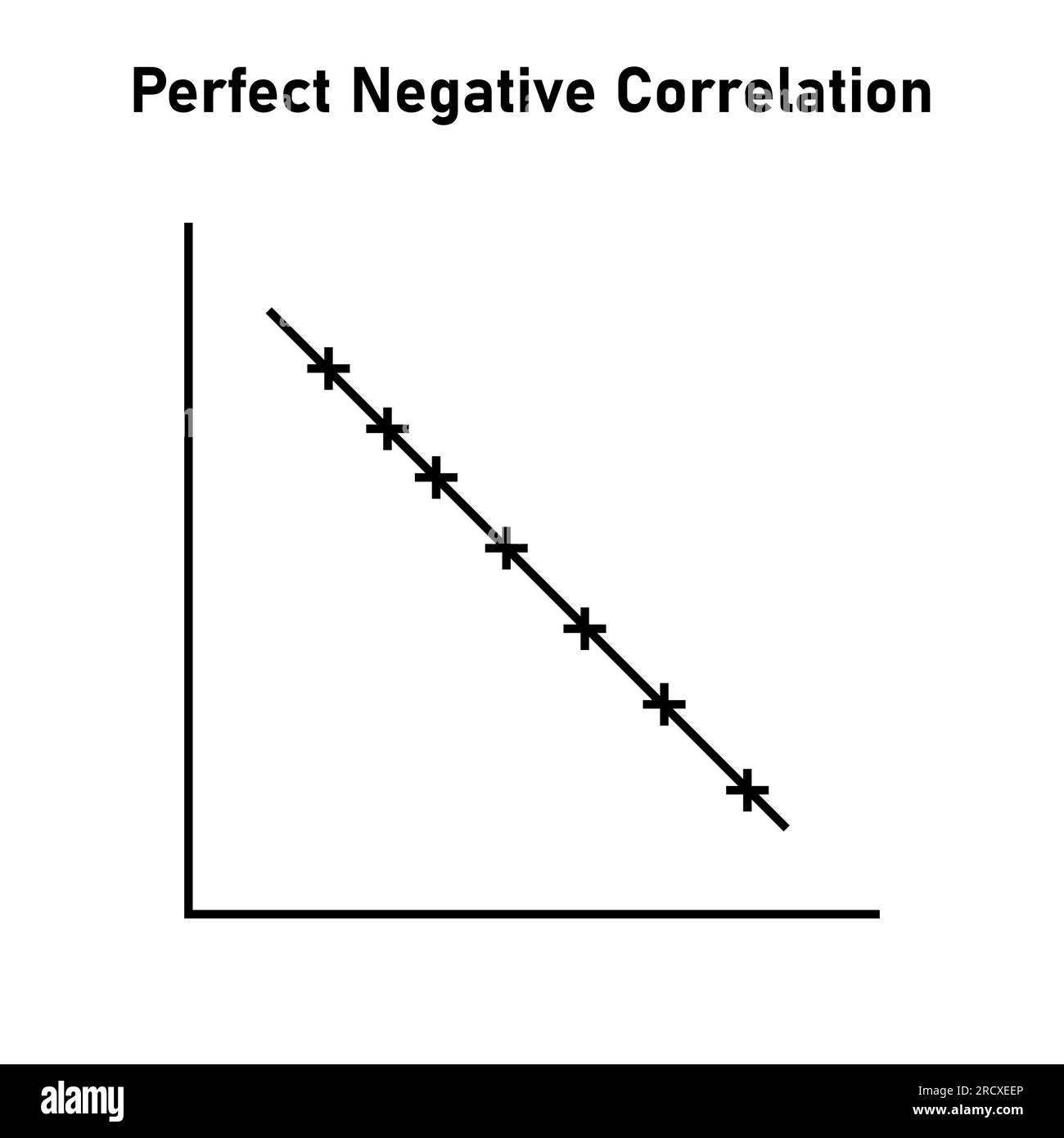
perfect negative correlation

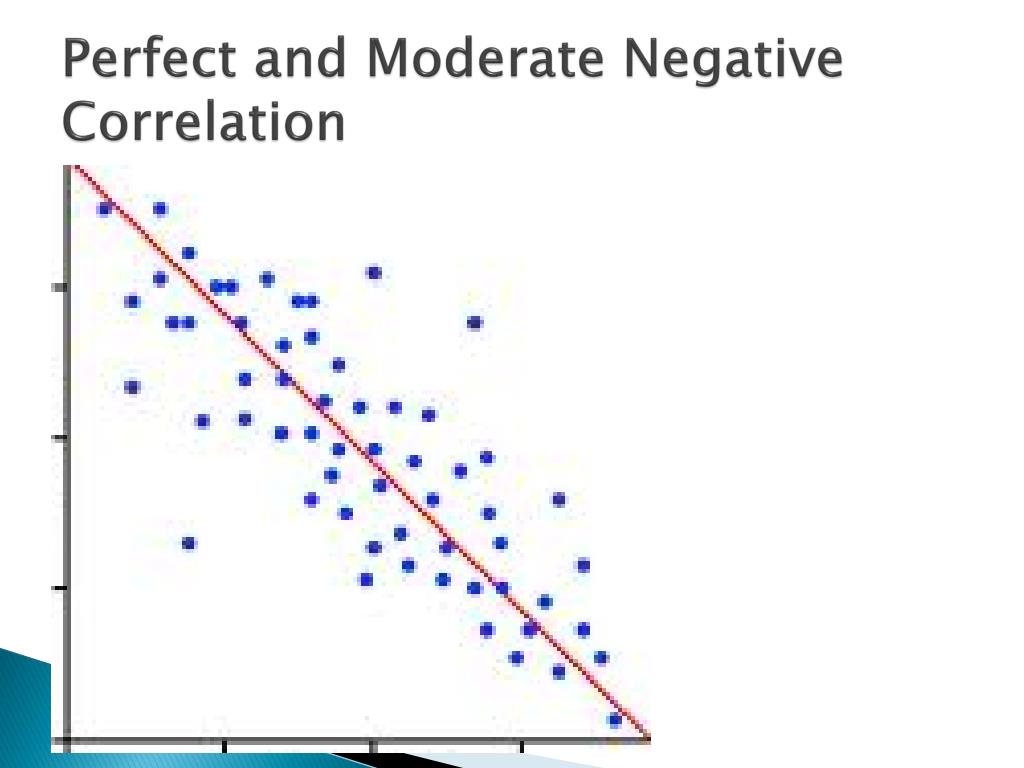
moderate negative correlation

circular no correlation

undefined correlation

curvilinear relationship

shows no correlation for pearson’s correlation

r²

proportion of shared variation

to what extent does the variation in x relate to the variation in y

allows for widening audience by allowing % of shared variation to be determined

indicates proportion of variation in x that has been observed in variation of y

problems of interpretation in coefficient

range restriction, selection effect and small sample — all give only part of the possible points on a scatter plot

artifact

something that appears to be true but is not

small proportion of shared variation

r= .25, r²= .06 = 6% of variation in x has been observed with variation in y

moderate proportion of shared variation

r=.50, r²= .25 = 25% of shared variation